1. 13. La compression à plusieurs étages La

1.13. La compression à plusieurs étages La limite de température. Si la grandeur du degré de l'augmentation de la pression () est assez haute, même au refroidissement fait des parois du cylindre, la température à la fin de la compression (T2) est inadmissible augmente. La limite de température est définie à la température de l'éclat des huiles de compresseur, qui se trouve dans la limite de Téc = 480...513 C. Pour la sécurité on accepte la température admissible Téc adm = (0,7...0,8)Téc . Selon “ aux Règles de la sécurité... ” Téc adm = 443 C. On sait que selon la formule (1.14): Ici le degré limite de l'augmentation de la pression. Ayant accepté T1 = 293 K, T2max = 443 K. Pour du procédé adiabatique de la compression de l'air est disponible np = 4,14. Ainsi, la pression effective possible au compresseur monoétagé compte tenu de l'aspect du procédé de la compression peut atteindre improbablement 4-5 bars. 1.13.1. Les raisons de l'application de la compression à plusieurs étages.

La limite volumineuse. Avec l'augmentation  s'accroît l'influence de l'espace nuisible. Au degré défini de l'augmentation de la pression le coefficient 1 deviendra égal au zéro, c'est-à-dire à la compression tout l'air s'installera dans l'espace nuisible. De la formule (1.25) : Pour le procédé isothermique à  = 0,1 max = 11, pour le procédé adiabatique max = 57,3. Ainsi, la raison principale est la limite de température.

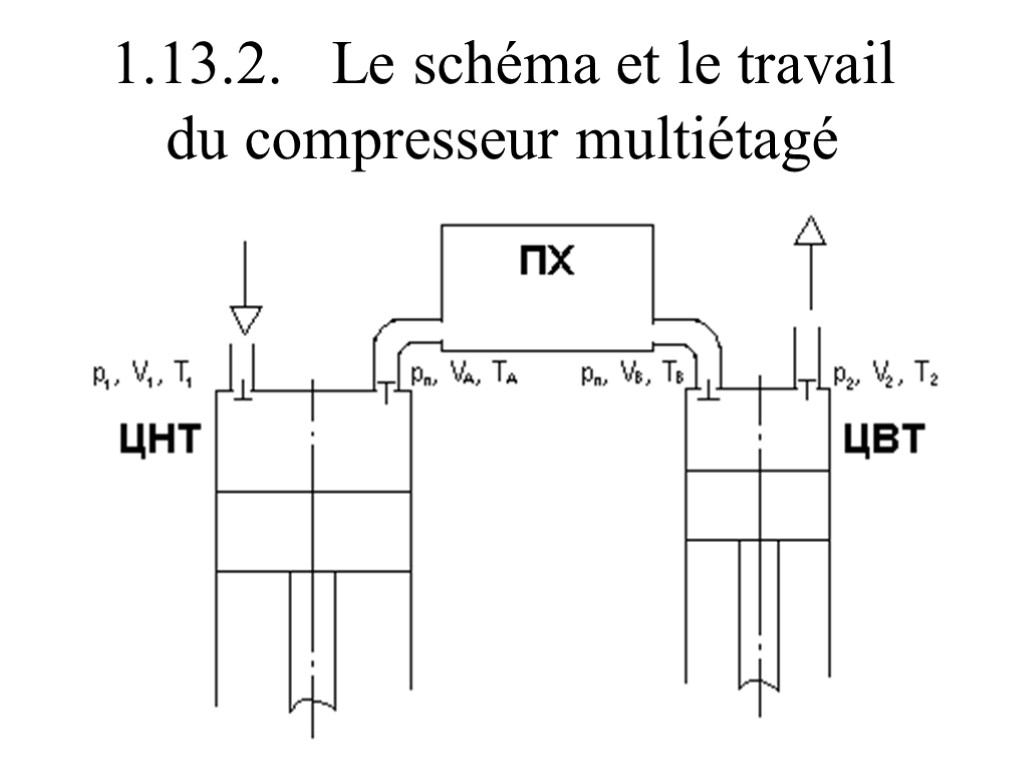
1.13.2. Le schéma et le travail du compresseur multiétagé

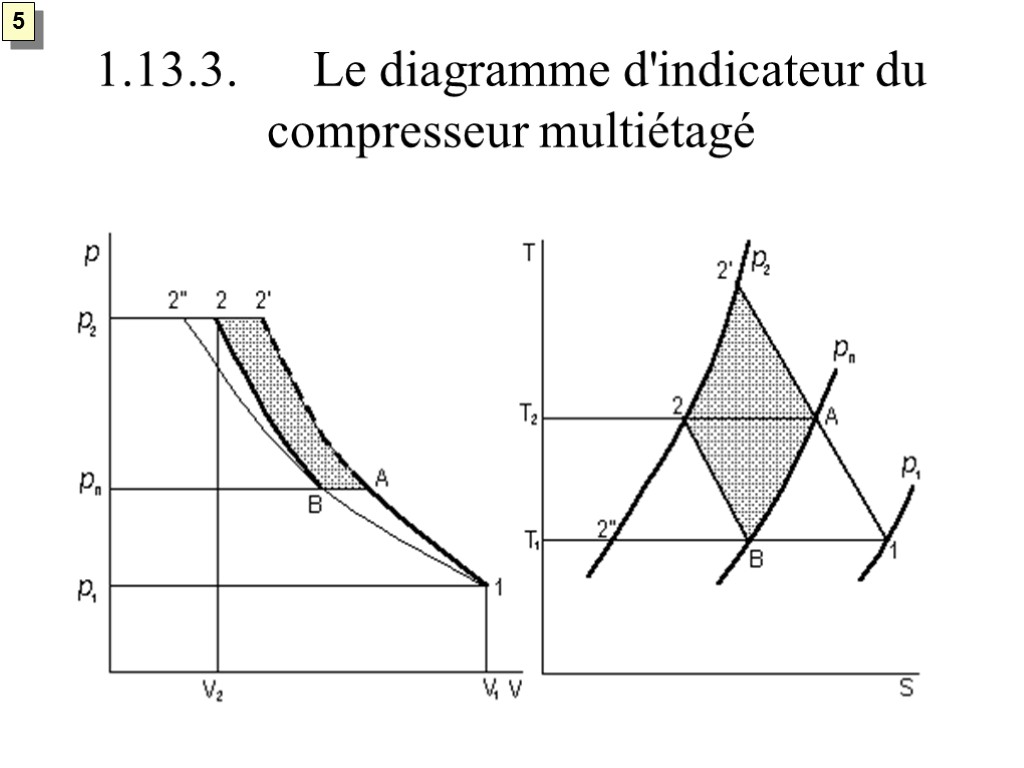
5 1.13.3. Le diagramme d'indicateur du compresseur multiétagé

1.13.4. La signification rationnelle de la pression intermédiaire La décomposition sur le degré de la compression à plusieurs étages est produite aux admissions suivantes principales: · Les lois de la compression de l'air dans tous les étages sont identiques; · Le refroidissement de l'air dans les réfrigérateurs intermédiaires est produit pour que la température de l'air au début de la compression dans tous les étages soit identique (Т1 = ТB); · L'énergie complète dépensée doit être plus petite. Nous définirons la pression intermédiaire la plus avantageuse Pn pour le compresseur à deux étages, avec celle-ci l'énergie complète dépensée sera minimale.

L'énergie dépensée dans le premier étage est définie selon la formule (1.12) : (1.12) Même pour le deuxième degré, en examinant celle-ci comme le compresseur particulier : (1.12) Puisque le refroidissement dans le réfrigérateur intermédiaire produit jusqu'à la température initiale

Puisque le refroidissement dans le réfrigérateur intermédiaire produit jusqu'à la température initiale (les points B et 1 se trouvent sur l'isotherme), Pп VВ = P1V1 , l'énergie totale dépensée: Pour la détermination de la pression Pn à qui l'énergie totale dépensée sera minimal, il est nécessaire le premier dérivé de L selon Pn assimiler au zéro et décider l'équation reçue par rapport à Pn.

l'équation reçue par rapport à Pn. Puisque P1V1 = const, d'où (1.32) Ainsi, la pression intermédiaire la plus avantageuse Pn pour le compresseur à deux étages est celle moyenne géométrique des pressions initiales et finales.

L'expression trouvée nous recopierons comme il suit : . Nous introduirons les désignations 1 = Pn / P1 - le degré de l'augmentation de la pression dans le premier étage et, par analogie, 2 = P2 / Pn - le degré de l'augmentation de la pression au deuxième étage;  = P2 / P1 - le degré complet de l'augmentation de la pression dans le compresseur. Ainsi 1 = 2. Mais , d'où . (1.33) Par analogie pour le nombre des étages z à la compression à plusieurs étages , (1.34) C'est-à-dire le degré de la compression en chacun des étages est égal à la racine du degré du nombre des étages du degré complet de la compression.

Les conclusions : - L'énergie dépensée dans chacun des degrés du compresseur sont identiques. En réalité, en examinant les formules (1.12), (1.12) et en prenant en considération le rapport reçu avant Pп VВ = P1V1 et est reçu L1c = L2c. - Les températures de l'air à la fin de la compression dans chacun des étages sont identiques. En fonction de la formule (1.15) pour chaque étage est disponible : ; Puisque pour les conditions de la décomposition au degré TВ = T1 et , Т1с = Т2с

Compte tenu des conclusions faites : L'énergie dépensée dans le compresseur à deux étages pour la production de l'air comprimé (1.35) - Même pour le compresseur à plusieurs étages (z - le nombre des étages) (1.36)

- La température de l'air à la fin de la compression : (1.37)

1.13.5 L'amélioration du coefficient volumineux du compresseur à la compression à plusieurs degrés En fonction de la formule (1.25) pour le compresseur bi-étagé la grandeur du coefficient volumineux On sait aussi, que le coefficient 1 est la relation du volume de l'air aspiré vers le volume décrit par le piston, c'est-à-dire 1 = Vs / Vn Lors de la compression bi-étagée le volume aspiré au premier étage de l'air Vs1 est plus grand, que Vs, puisque l'élargissement de l'air de l'espace nuisible commençant de la pression Рп  Р2 , finit plus vite. La grandeur du coefficient volumineux 1 = Vs1 / Vn ou

Même pour le compresseur à plusieurs étages (1.39) Nous comparons les coefficients volumineux des compresseurs mono- et bi-étagés ayant les espaces identiques “nuisibles” b = 0,05, les degrés complets de l'augmentation de la pression  = 8 et les procédés polytropiaues de la compression m = 1,3. Selon la formule (1.25) pour le compresseur à un étage 1 = 1 - 0,05(81/1,3- 1) = 0,812. Selon la formule (1.38) pour le compresseur bi-étagés 1 = 1 - 0,05(81/(21,3)- 1) = 0,938. Ainsi, l'amélioration fait 12,6 %.

1.14 Les caractéristiques de débit du compresseur et des réseaux. Le régime de travail Pour la définition des paramètres de travail de l'installation pneumatique il est nécessaire de savoir les caractéristiques du compresseur, ainsi que du réseau. 1.14.1 La caractéristique de débit du compresseur à piston La caractéristique de débit du compresseur à piston représente la dépendance de la productivité du compresseur de la pression dans le raccord de tuyau forcé. La caractéristique de débit du compresseur théorique à piston est décrite par la formule (1.28) : . Des grandeurs, entrant dans la formule donnée, théoriquement seulement la fréquence de la rotation peut dépendre de la pression, mais, puisque les compresseurs des installations stationnaires sont entraînés par les électromoteurs synchrones, on peut croire, que la productivité théorique du compresseur ne dépend pas de la pression.

Il convient les caractéristiques des compresseurs à piston d'examiner dans les coordonnées suivantes : Q Qt Q P La caractéristique de débit du compresseur réel : Q = Qt  = Qt 1 2 3 , Où 1 et 3 dépendent de la pression.

1.14.2 La caractéristique de débit du réseau pneumatique de la mine La caractéristique du réseau peut être exprimée par le moyen suivant : Р = Рп + Рс - Рг . Ici : P - la pression du compresseur; Pn - la pression du consommateur; Pc - la perte de la pression au réseau; Рг - la pression liée à l'hauteur géométrique, Рг = g Hг Q n1 n2 n1>n2 P

La propriété du réseau : La propriété du réseau : le réseau possède la capacité. La capacité est le pouvoir d'accumuler l'air. Si au réseau entre plus d’air, qu'est pris du réseau, la pression dans celle-ci grandit, et - au contraire.

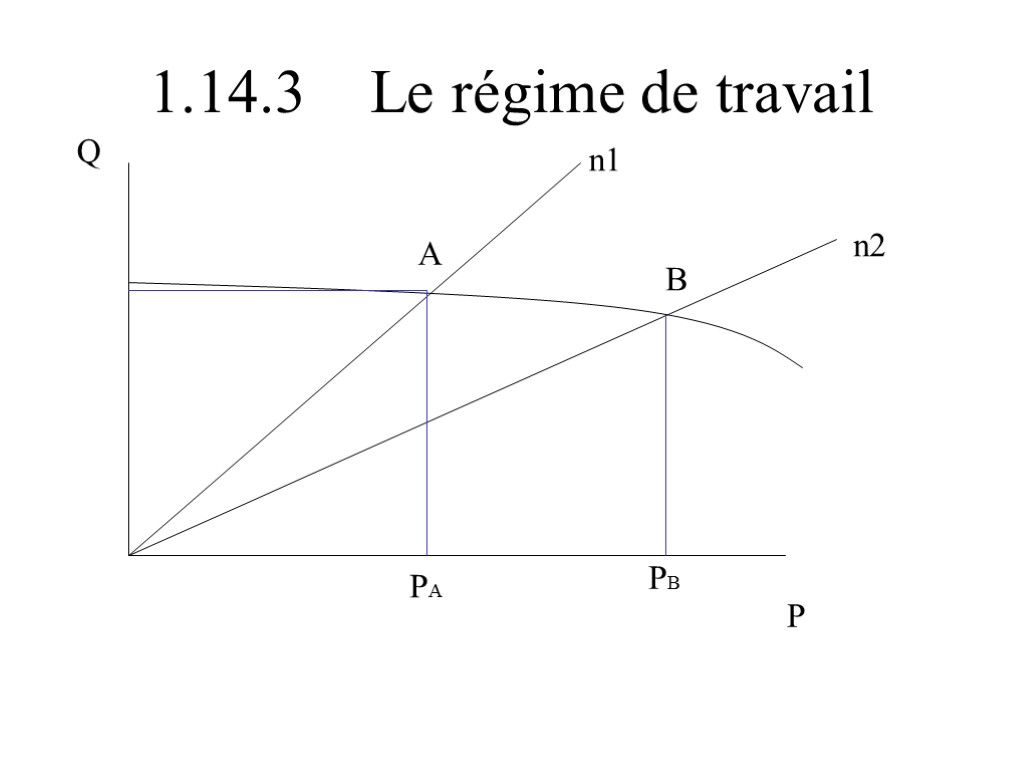
1.14.3 Le régime de travail Q P n1 n2 A B PA PB