1 1 Уравнение неразрывности 2 Уравнение движения

1

1. Уравнение неразрывности 2. Уравнение движения 3. Уравнение Бернулли. Для какого движения справедливо это уравнение 4. Записать силу давления для идеальной жидкости 2

3

Пусть внешние силы равны нулю, а жидкость покоится. В течении короткого интервала времени действует градиент давления и возникает движение. Умножим на dt и проинтегрируем уравнение движения от 0 до . 4

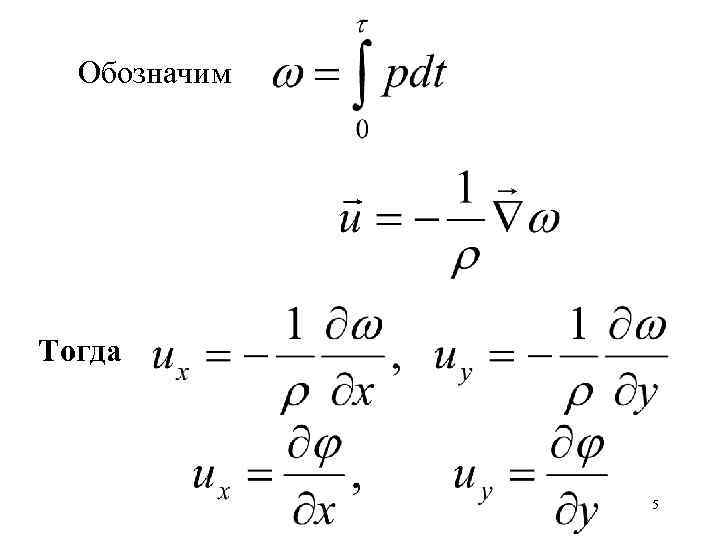Обозначим Тогда 5

Получаем: Потенциал скорости представляет собой систему импульсных давлений, отнесенных к плотности жидкости, которая бы привела жидкость из состояния покоя в движение со скоростью u. Это истолкование дано Коши и Пуассоном в 1816 г. 6

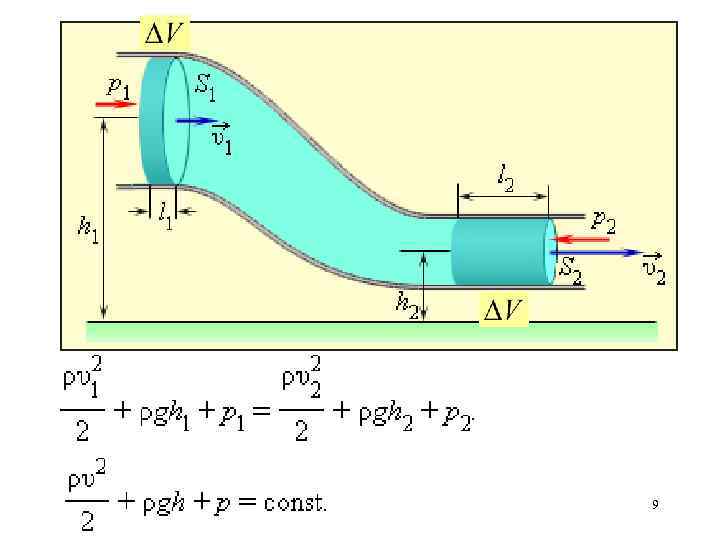
Интеграл уравнения движения для стационарного потока несжимаемой жидкости Для стационарного движения выполняется вдоль линии тока Для безвихревого движения -( ) выплняется везде 7

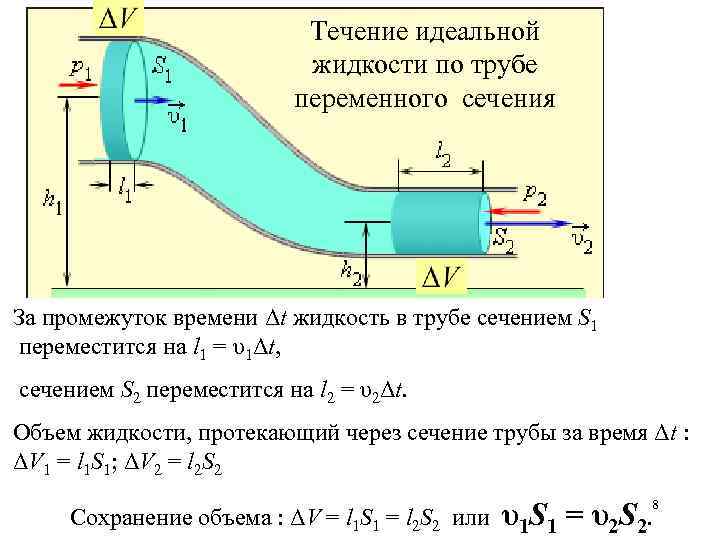Течение идеальной жидкости по трубе переменного сечения За промежуток времени Δt жидкость в трубе сечением S 1 переместится на l 1 = υ1Δt, сечением S 2 переместится на l 2 = υ2Δt. Объем жидкости, протекающий через сечение трубы за время Δt : ΔV 1 = l 1 S 1; ΔV 2 = l 2 S 2 Сохранение объема : ΔV = l 1 S 1 = l 2 S 2 или υ1 S 1 = υ2 S 2. 8

9

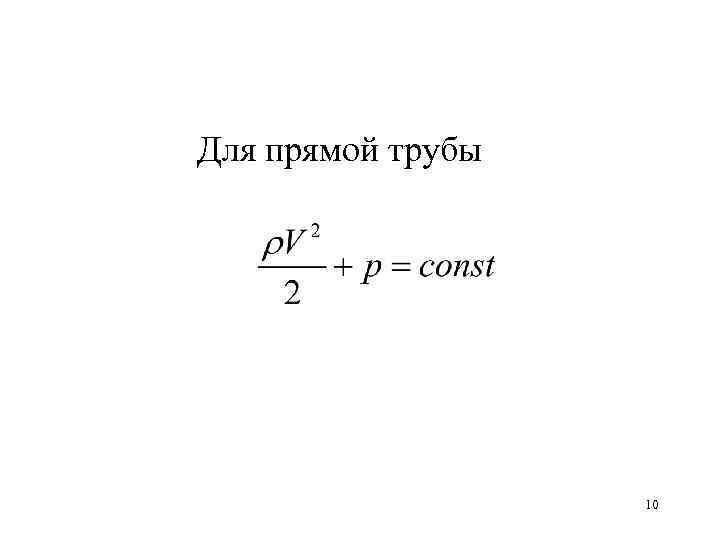Для прямой трубы 10

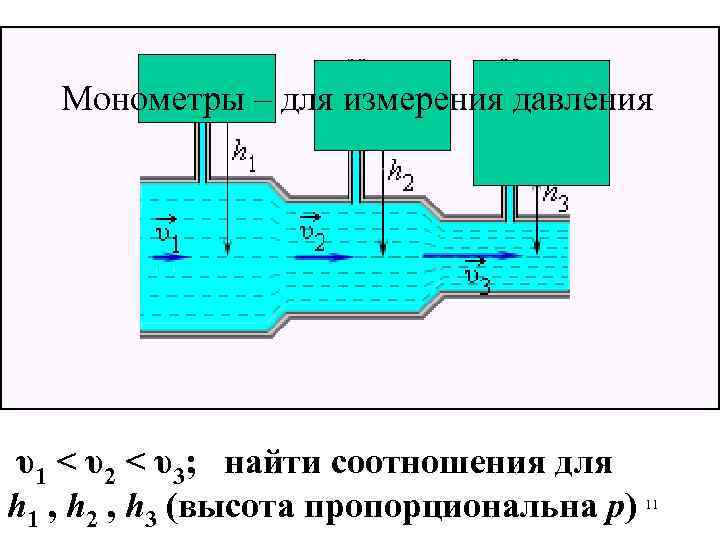Монометры – для измерения давления υ1 < υ2 < υ3; найти соотношения для h 1 , h 2 , h 3 (высота пропорциональна р) 11

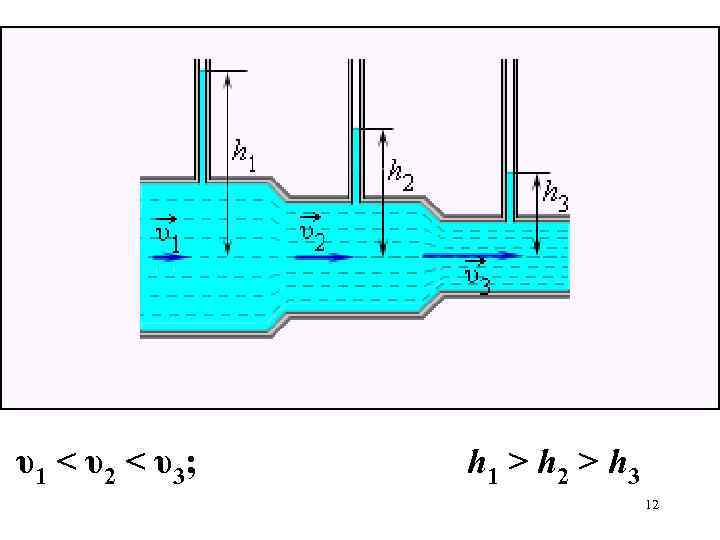υ1 < υ2 < υ3; h 1 > h 2 > h 3 12

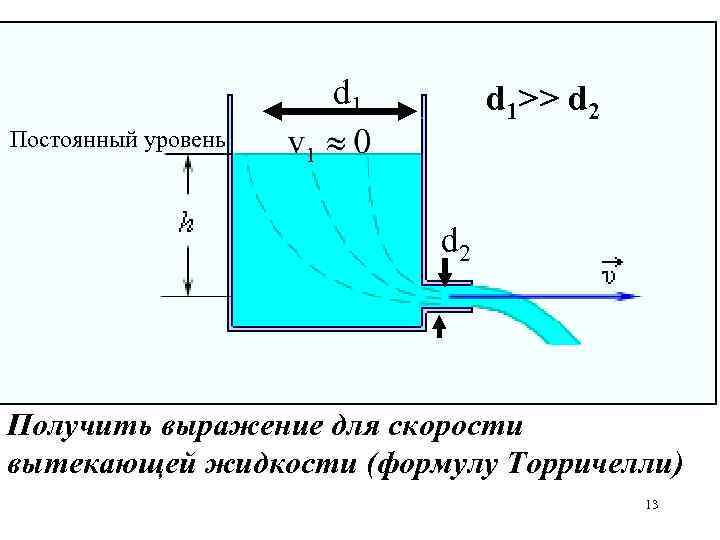d 1 d 1>> d 2 Постоянный уровень d 2 Получить выражение для скорости вытекающей жидкости (формулу Торричелли) 13

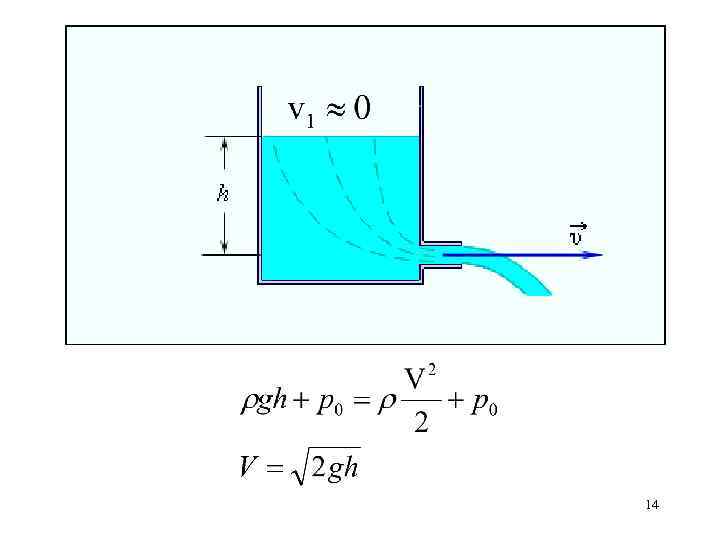14

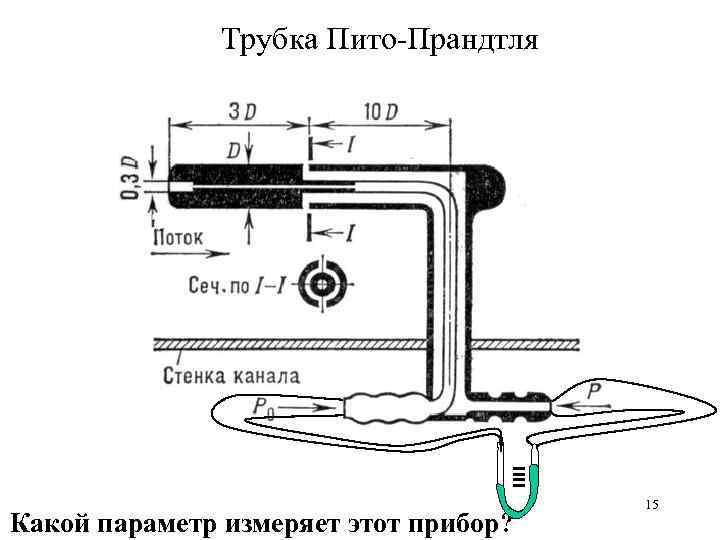Трубка Пито-Прандтля Какой параметр измеряет этот прибор? 15

ПОЛУЧИТЬ интеграл движения для нестационарного безвихревого течения идеальной однородной несжимаемой жидкости в поле потенциальных сил. 16

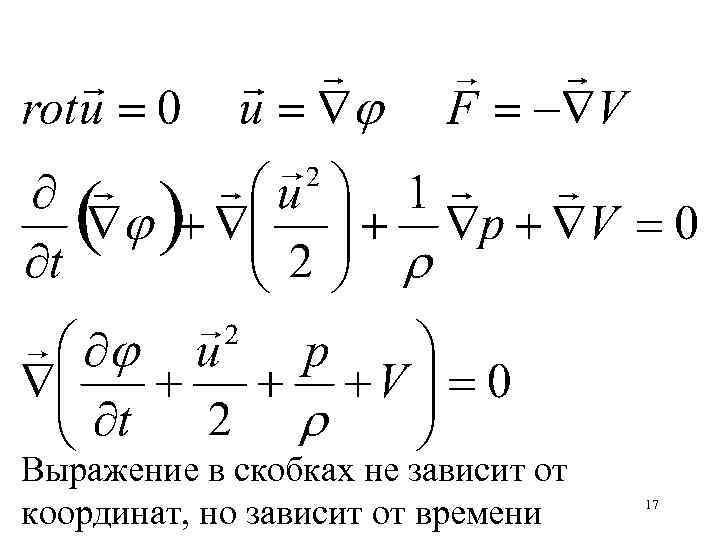Выражение в скобках не зависит от координат, но зависит от времени 17

Получаем интеграл Коши Где f(t) произвольная функция времени 18

Показать, что существование интегралов Бернулли, Бернулли-Эйлера и Коши накладывает ограничение на скорость течения жидкости 19

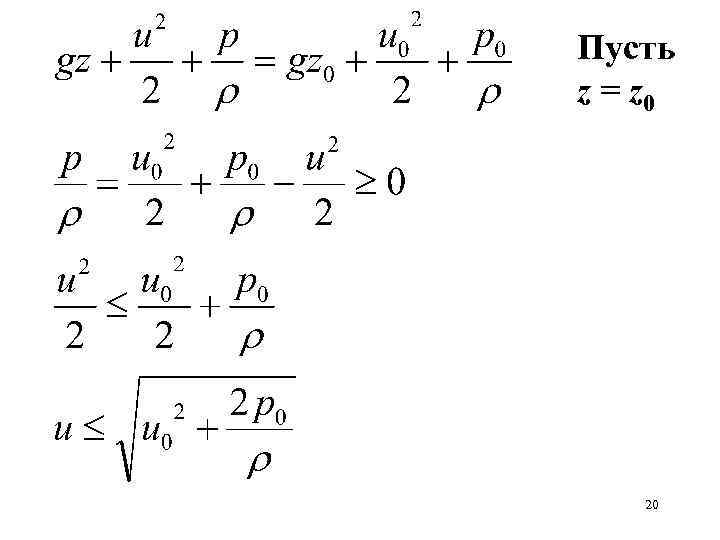Пусть z = z 0 20

21

К правой и левой части применяем операцию rot (при этом теряем часть решений) 22

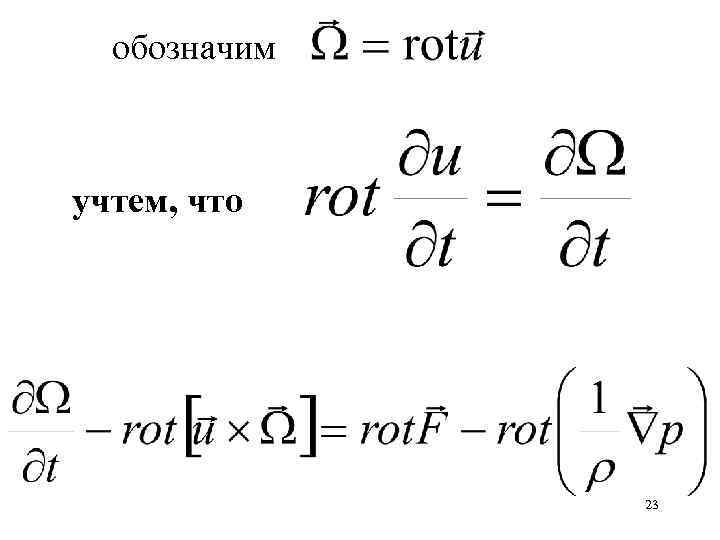обозначим учтем, что 23

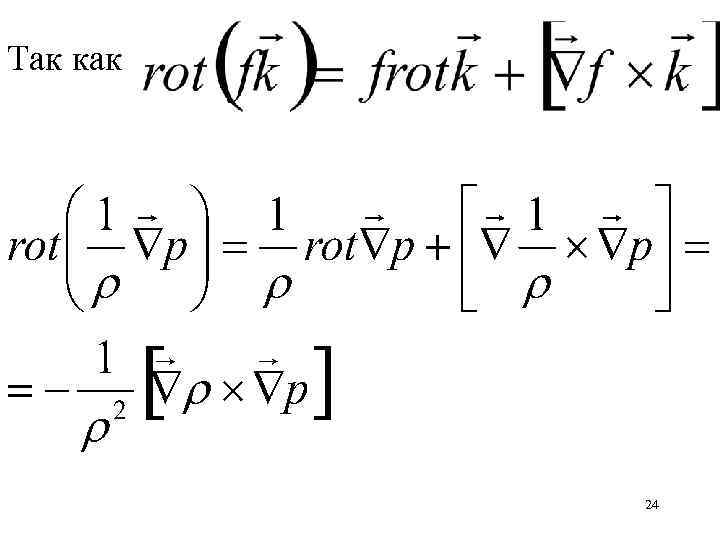Так как 24

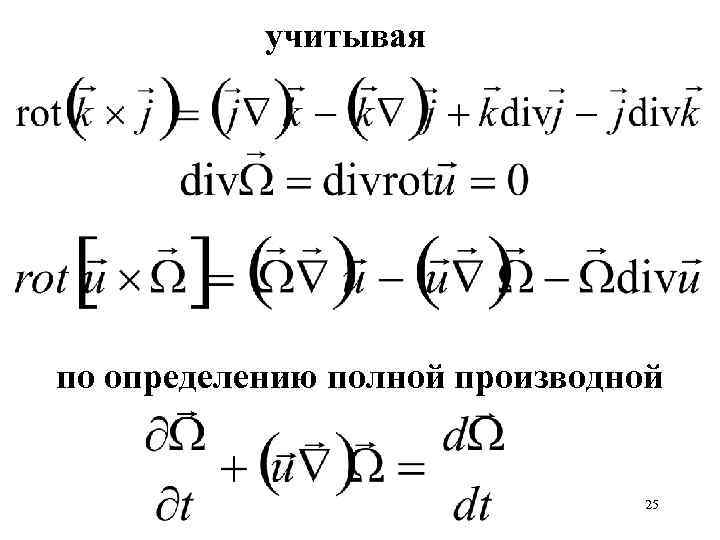учитывая по определению полной производной 25

плотность давление Записать уравнение Фридмана для течения идеальной жидкости в случае: 1. Несжимаемая жидкость 2. Внешние силы потенциальны 3. Плотность – функция только давления 26

1)Пусть внешние силы потенциальны 2) плотность является функцией только давления 3)жидкость несжимаема 27

Если уравнение выполняется во всей области и в любой момент времени, то выполняется необходимое и достаточное условие, чтобы сохранялись вихревые линии и циркуляция скорости (интенсивность вихревых трубок) 28

Уравнение Гельмгольца для несжимаемой жидкости однородной по плотности , где Если , то вихрь скорости сохраняется 29

Если в момент времени t=0 в жидкости нет вихрей они не возникнут и в любой другой момент времени. Если ротор скорости отличен от нуля, то завихренность остается неизменной во времени 30

Сохраняется ли вихрь для потока со сдвигом скорости у ux=u 0 + y, uy=0, uz=0 z х 31

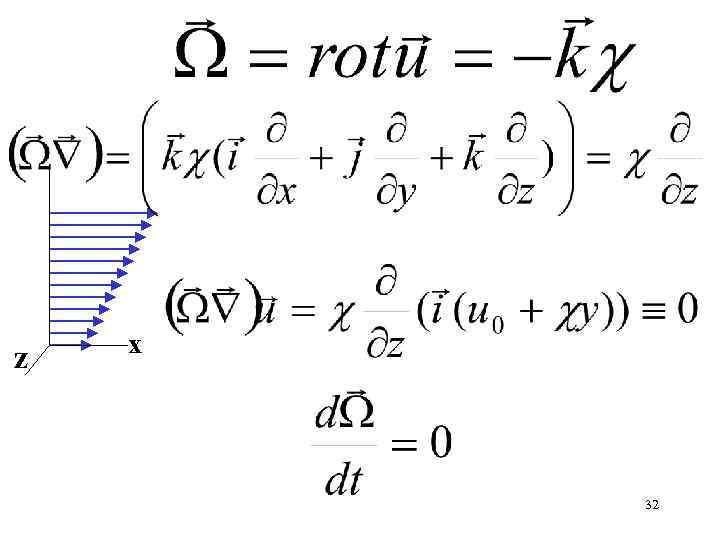z х 32

Проверить Выполняется ли уравнение Гельмгольца для движения несжимаемой жидкости, если скорость задана выражениями: ux= z, uy= - z, uz= y - x 33

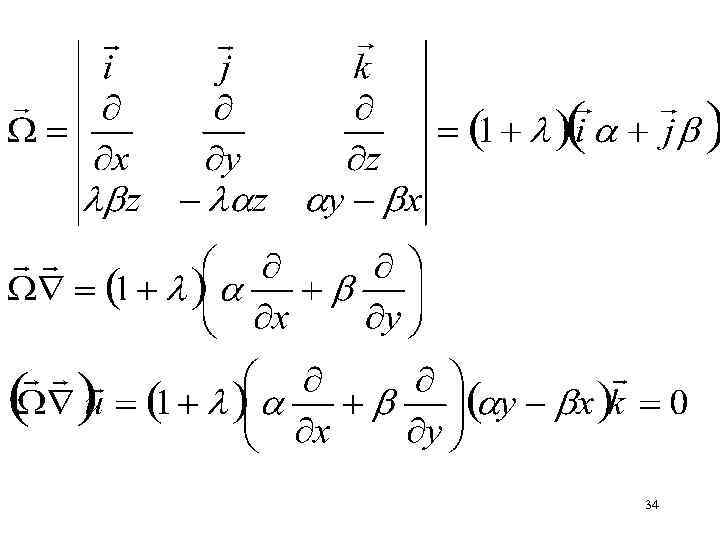34

плотность давление Записать уравнение Фридмана для течения идеальной жидкости в случае: 1. Несжимаемая жидкость 2. Внешние силы потенциальны 3. Плотность – функция только давления 35

1)Внешние силы не имеют потенциала 2) плотность является функцией не только давления 3)жидкость сжимаема 4) Ушли градиенты параметров из основного уравнения применении операции rot 36

у у>0 воздух без водяных паров Бесконечная пластина равномерно нагрета, температура воздуха ниже температуры пластины вдали от нее Построить линии равной плотности в тонком слое воздуха над пластиной Построить вектор градиента плотности 37

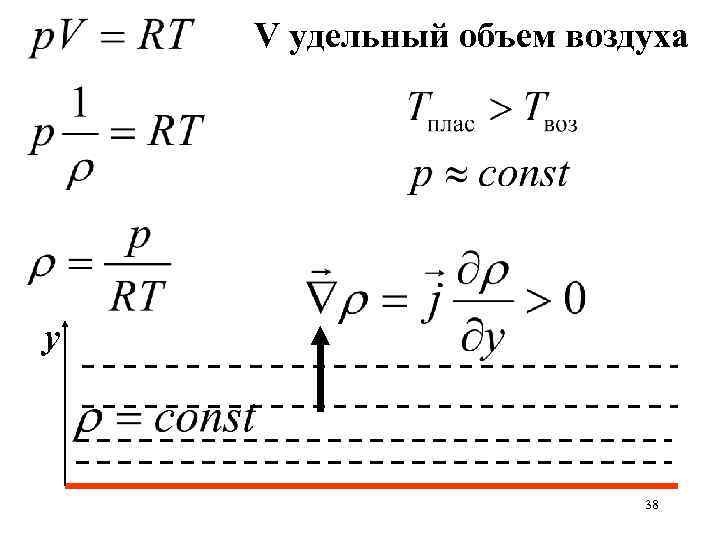V удельный объем воздуха у 38

у у>0 воздух без водяных паров Бесконечная пластина неравномерно нагрета, температура воздуха ниже температуры пластины вдали от нее Построить линии равной плотности в тонком слое воздуха над пластиной Построить вектор градиента плотности 39

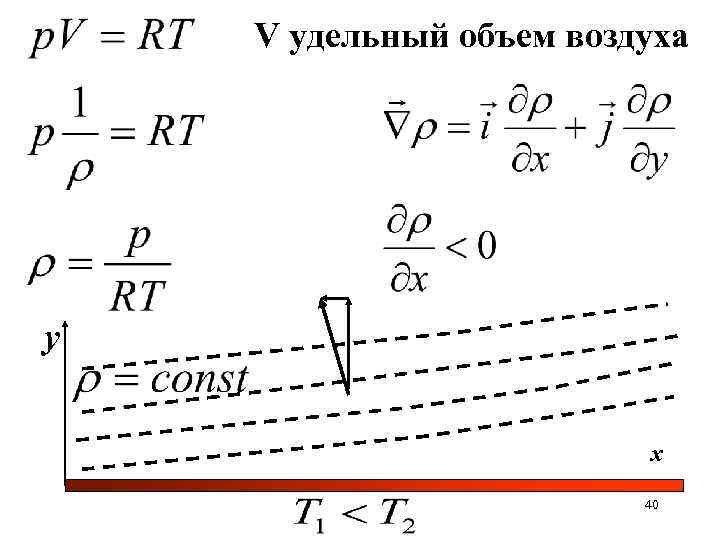V удельный объем воздуха у х 40

Термики, всплывающие от нагретой поверхности. Грибообразные столбики периодически поднимаются от нагретой медной пластинки. Визуализация осуществляется электрохимическим путем с помощью подкраски тимолом-синим. На правом снимке скорость нагрева выше. [Sparrow, 41 Husar, Goldstein, 1970]

42

Закон Гей-Люссака: при постоянном давлении плотность есть функция температуры. const P= =const экватор 43

В результате неравномерного прогрева атмосферы Земли линии равной плотности и равного давления (изопикны и изобары) не параллельны другу. В результате в атмосфере зарождаются вихри планетарного масштаба, определяющие господствующие ветры. От 30 широт к экватору – пассаты, С охлажденных материков в теплый океан (или наоборот летом) - муссоны 44

45

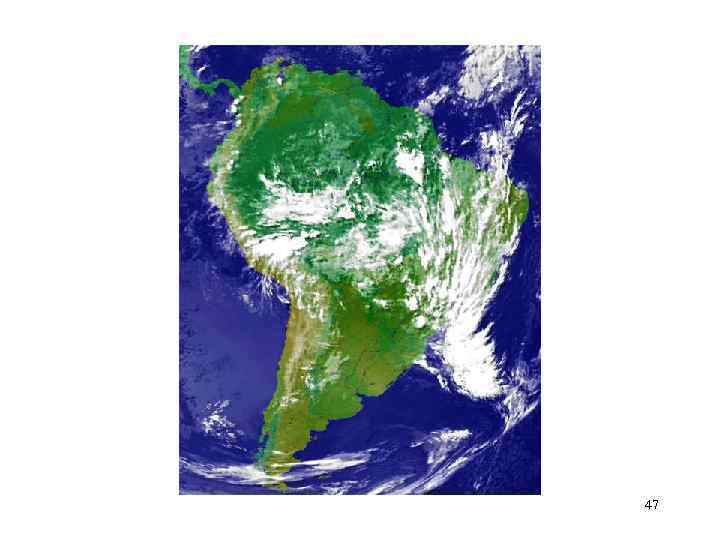
При нормальных погодных условиях у берегов Перу дуют два ветра: а) пассат над океаном на север б) сильный ветер с берега в океан Под действием пассата и силы Кориолиса теплая вода перемещается от берега на запад. Ветер с материка тоже отгоняет поверхностную воду от берега. 46

47

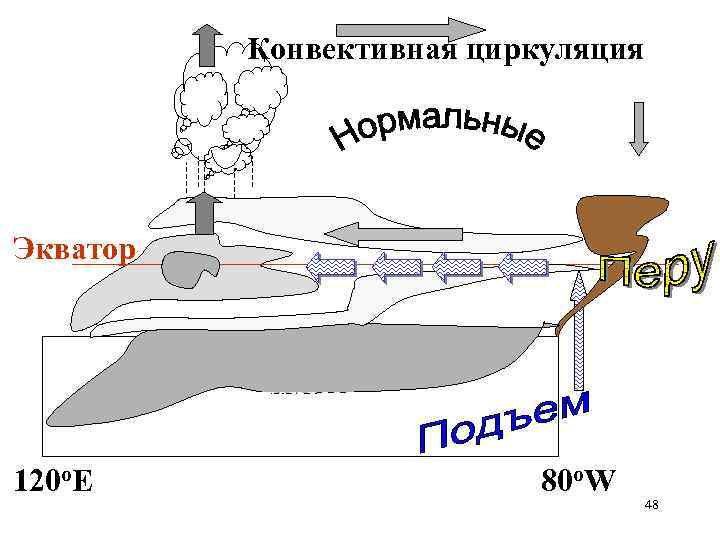Конвективная циркуляция Экватор термоклин 120 o. E 80 o. W 48

В результате у берегов Перу холодная богатая питательными веществами вода поднимется из глубинных слоев к поверхности океана, что приводит к быстрому росту массы планктона. Это обеспечивает изобилие рыбы. 49

Изобилие рыбы определяет объемы предложения и потребления рыбы на всем побережье. 50

-сезонное явление, случается ежегодно у берегов Перу. При возникновении резко сокращается улов рыбы. заключается в том, что меняется обычное движение поверхностных вод океана : вместо движения от берега Перу в 5 открытый океан, вода течет вдоль берега. 1

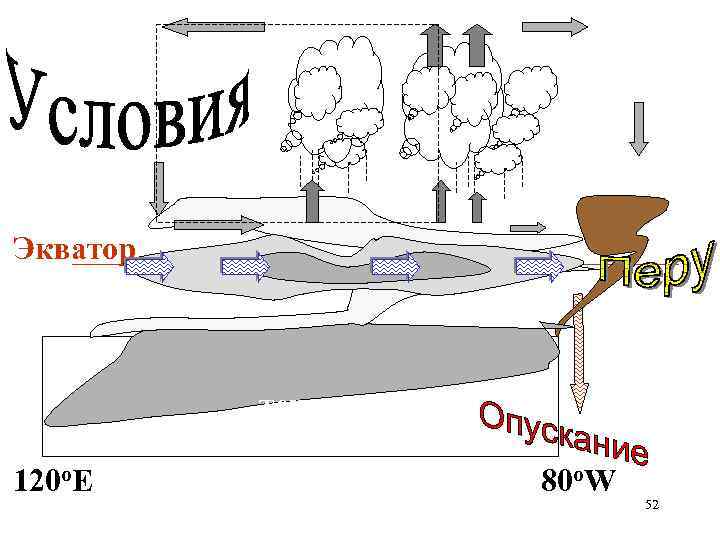Экватор термоклин 120 o. E 80 o. W 52

Во время зимнего солнцестояния материк сильно прогревается. В результате происходит ослабление интенсивности ветра с берега. В это же время происходит ослабление пассата (но не его разворот, как часто утверждается), господствующего в северном направлении 53

В этих условиях движение поверхностных вод может поменять направление на противоположное, предотвращая подъем глубинных вод. 54

- сезонное явление. Обратный ток воды может возникнуть, но может и нет. Продолжительность явления зависит от величины суммарной радиации, поступающей от Солнца. - охраняет перуанское рыбное стадо, отдыхающее в течение «естественного» закрытого сезона. Инерция дрейфового течения сокращает сроки действия 55

Если сроки действия увеличиваются, на побережье начинаются голод и эпидемии. Такие события появляются с периодом 11 лет. 1982 -83, 1990 -91, 1997 -98. В этот период появляются и другие катастрофические явления (ураган Лили 2002). 56

назван испанскими миссионерами. Это же название использовал Humboldt в 1802 г. , объясняя явление космическими силами. относится к климатическим явлениям, названным Бьеркнесом (1969) «южные осцилляции» . Рассмотренные выше ветры обусловлены существованием областей высокого и низкого давления, возникающими в результате глобальной циркуляции в атмосфере. 57

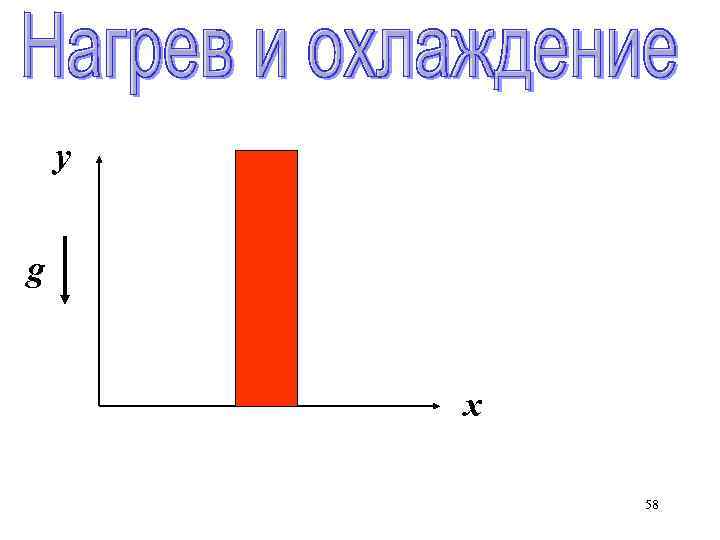у g х 58

nst co P=const холод = = con st нагрев P=const 59

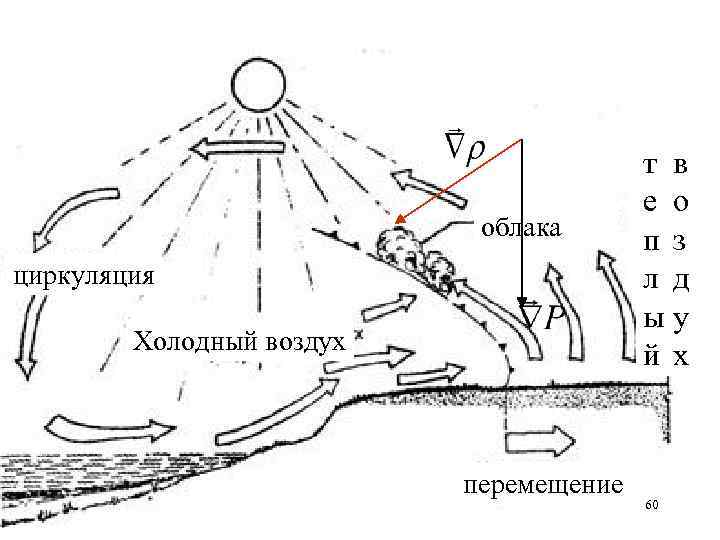облака циркуляция Холодный воздух перемещение т в е о п з л д ыу й х 60

Куда дует ветер утром, когда температура суши ниже, чем температура воды в море? 61

Бриз - ветер в море с охлажденной за ночь суши. 62

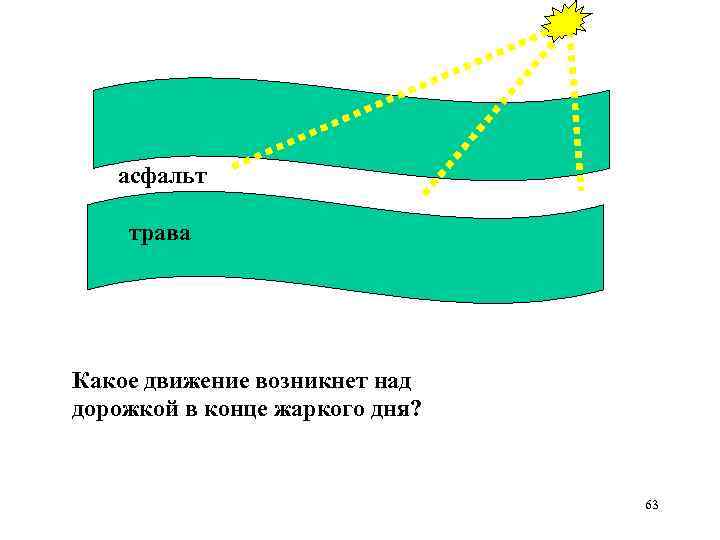асфальт трава Какое движение возникнет над дорожкой в конце жаркого дня? 63

64

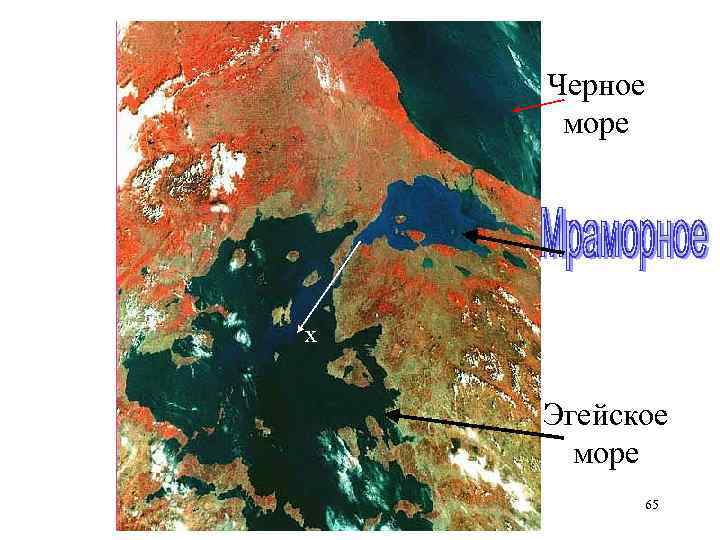Черное море х Эгейское море 65

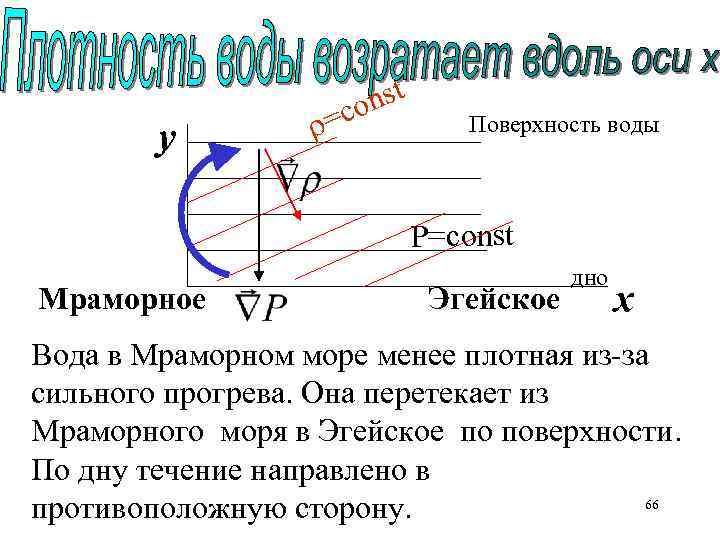y nst =co Поверхность воды P=const Мраморное Эгейское дно х Вода в Мраморном море менее плотная из-за сильного прогрева. Она перетекает из Мраморного моря в Эгейское по поверхности. По дну течение направлено в 66 противоположную сторону.

Средиземное море 67

Накопленное верхними слоями океана в низких широтах солнечное тепло переносится летом теплыми течениями (такими, как Гольфстрим и Куросио) в умеренные. В холодный период года океан в высоких широтах отдает его в атмосферу. Это один из основных механизмов воздействия океана на климат. Однако во фронтальной зоне (т. е. в области больших градиентов температуры и солености) тепло и соль переносят не только течения, но и синоптические вихри океана. 68

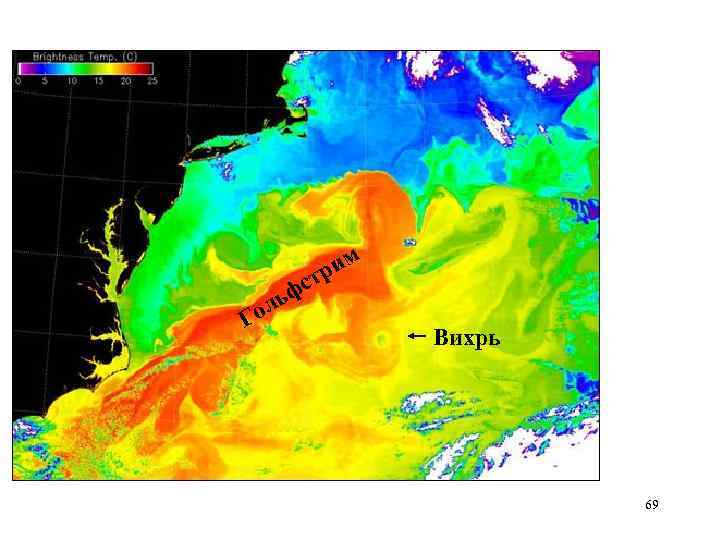и тр с м ф ь ол Г Вихрь 69

Вихри имеют масштаб порядка 70 – 80 км. Скорость орбитального движения быстро уменьшается с глубиной. В верхнем слое толщиной около 500 м скорость вращения достигает 40 -45 см/c. На глубине 1400 м орбитальная скорость уменьшалась до 10 см/с. Скорость перемещения вихрей в генеральном направлении на запад составляет от 2 до 10 см/c. Интенсивные вихри переносят вместе с собой содержавшуюся в них воду. Время жизни - 3 -4 месяца. 70

В Тихоокеанском океанологическом институте РАН, начиная с 80 -х годов 20 века, ведутся наблюдения за большими вихрями, формирующимися на западе Тихого океана, в зоне слияния двух главных течений этого региона: Ойясио и Курасио. Вихри медленно движутся на северо-восток вдоль всей длины Курило. Камчатского желоба против основного потока Ойясио в субарктические воды. 71

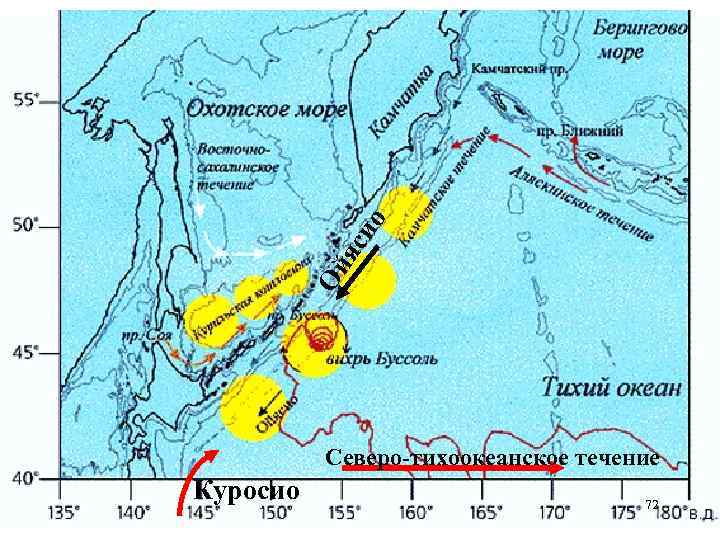ио яс Ой Северо-тихоокеанское течение Куросио 72

73

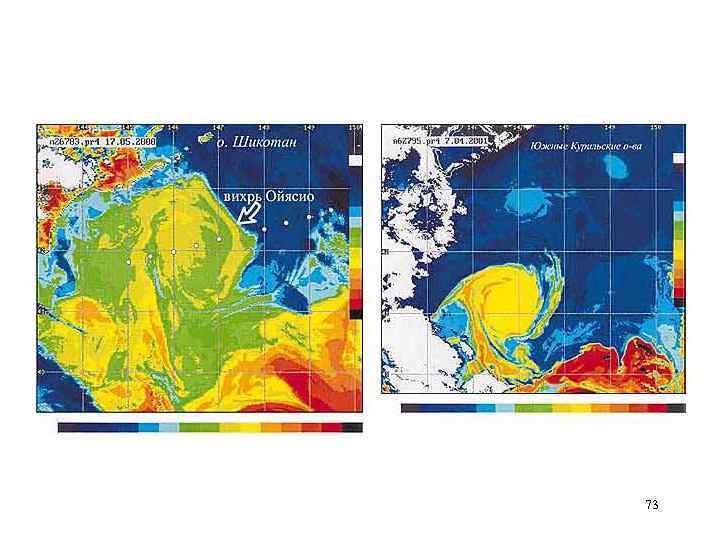
Вихрь, названный WCR 86 B (вихрь течения Куросио 1986 г. с теплым ядром), отделился от течения Куросио примерно у 37°с. ш. и двигался вдоль желоба против течения на северо-восток со скоростью около 1 -2 см/с. В сентябре 1990 г. он достиг широты пролива Буссоль (46. 5°с. ш. ), отделяющего южную группу Курильских островов от средней группы. 74

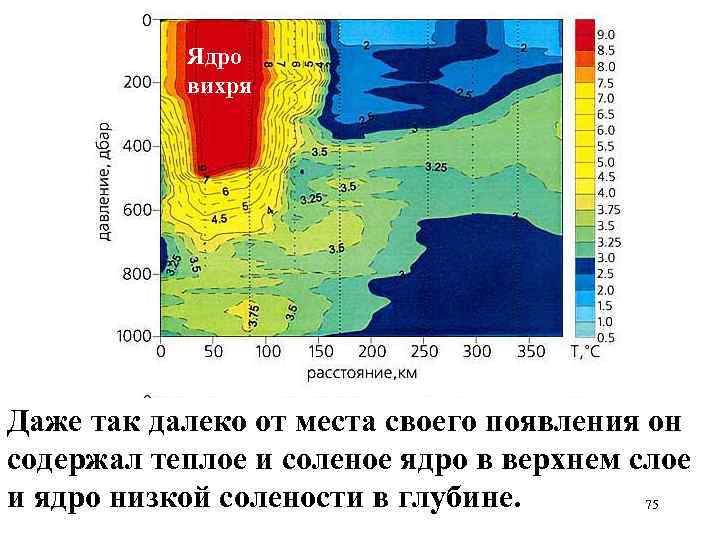Ядро вихря Даже так далеко от места своего появления он содержал теплое и соленое ядро в верхнем слое и ядро низкой солености в глубине. 75

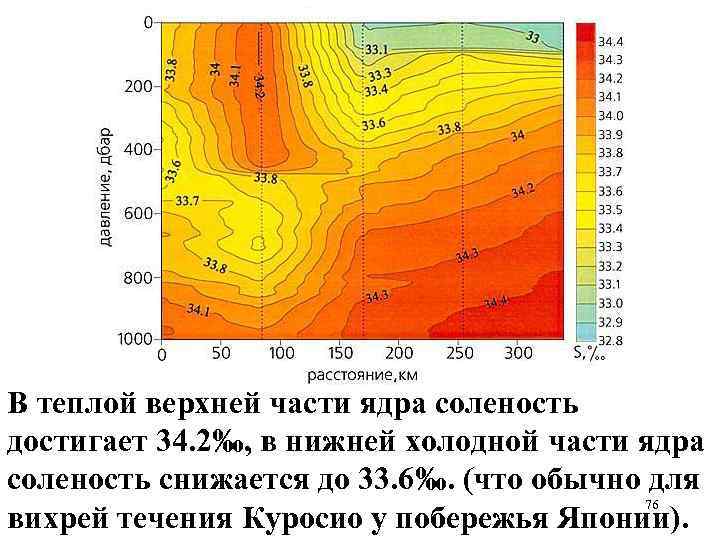В теплой верхней части ядра соленость достигает 34. 2‰, в нижней холодной части ядра соленость снижается до 33. 6‰. (что обычно для 76 вихрей течения Куросио у побережья Японии).

Особенно интересна продолжительность жизни вихрей течений Куросио и Ойясио. Казалось бы, они должны разрушаться из-за турбулентной диссипации, как антициклонические вихри Гольфстрима. Вместе с тем, вихрь WCR 86 B, зародившись в 1986 г. , продолжал двигаться вдоль Курило-Камчатского желоба еще в конце 1991 г. , то есть существовал более пяти лет. Слежение за вихрем проводилось с помощью последовательных съемок на судах Тихоокеанского океанологического института и непрерывных спутниковых изображений, принятых и обработанных в Институте автоматики и 77 процессов управления ДВО РАН.

Вихри в пограничных слоях потоков жидкости 78

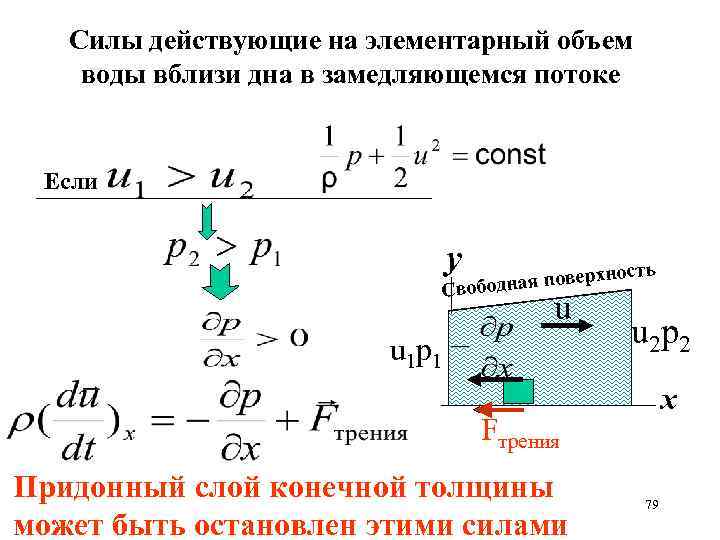Силы действующие на элементарный объем воды вблизи дна в замедляющемся потоке Если y хно дная повер Свобо u u 1 p 1 сть u 2 p 2 х Fтрения Придонный слой конечной толщины может быть остановлен этими силами 79

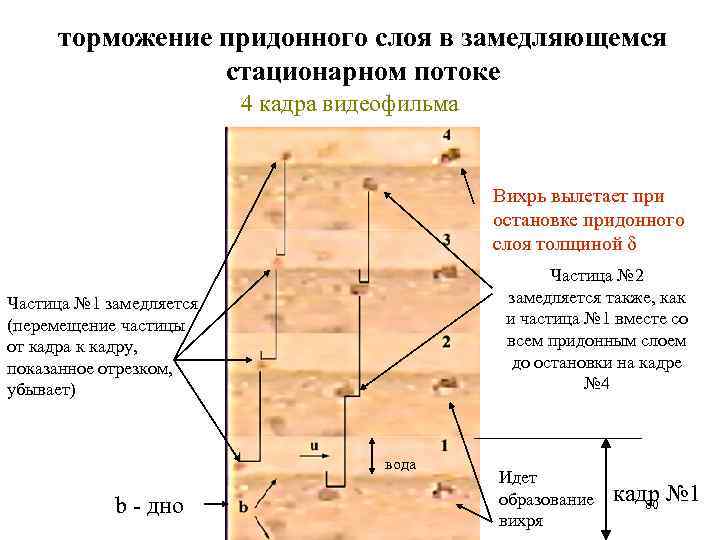торможение придонного слоя в замедляющемся стационарном потоке 4 кадра видеофильма Вихрь вылетает при остановке придонного слоя толщиной d Частица № 2 замедляется также, как и частица № 1 вместе со всем придонным слоем до остановки на кадре № 4 Частица № 1 замедляется (перемещение частицы от кадра к кадру, показанное отрезком, убывает) вода b - дно Идет образование вихря кадр № 1 80

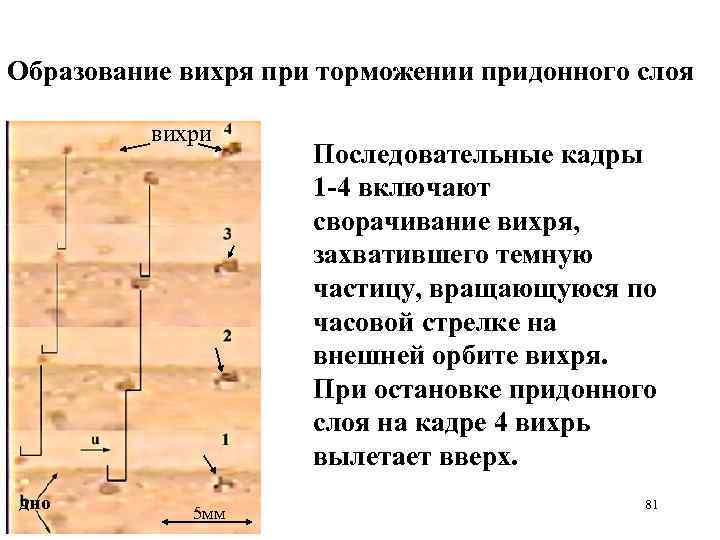Образование вихря при торможении придонного слоя вихри дно 5 мм Последовательные кадры 1 -4 включают сворачивание вихря, захватившего темную частицу, вращающуюся по часовой стрелке на внешней орбите вихря. При остановке придонного слоя на кадре 4 вихрь вылетает вверх. 81

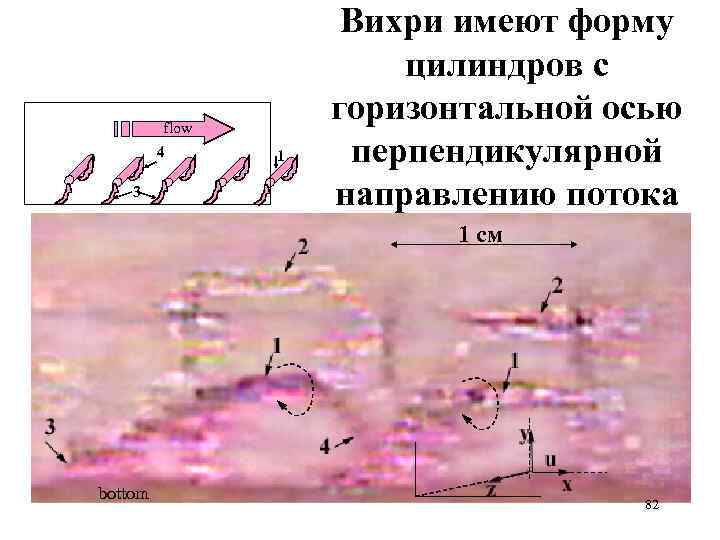flow 4 3 1 Вихри имеют форму цилиндров с горизонтальной осью перпендикулярной направлению потока 1 см bottom 82

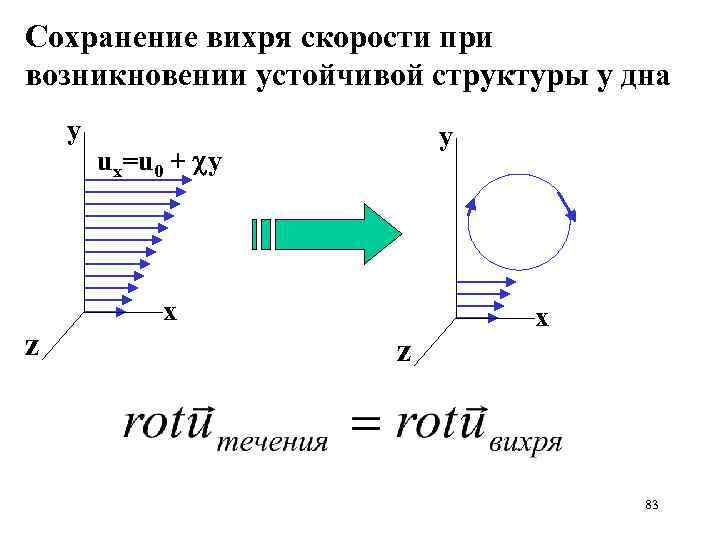Сохранение вихря скорости при возникновении устойчивой структуры у дна у у ux=u 0 + y х z 83

Угловая скорость вращения вихря w, возникающего в сдвиговом слое потока y