f984a533bcb7584f990bfb226807e8c7.ppt
- Количество слайдов: 48

1. 1 Problem Solving with Fractions • Addition words Ø Plus, more than, added to, increased by, sum, total, sum of, increase of, gain of • Subtraction words Ø Less, subtracted from, difference, less than, fewer, decreased by, loss of, minus, take away

1. 1 Problem Solving with Fractions • Multiplication words Ø Product, double, triple, times, of, twice as much • Division words Ø Divided by, divided into, quotient, goes into, divided equally per • Equals Ø Is, the same as, equal to, yields, results in, are

1. 1 Problem Solving • Changing word phrases to expressions: The sum of a number and 9 x+9 7 minus a number 7 -x Subtract 7 from a number x– 7 The product of 11 and a number 11 x 5 divided by a number The product of 2 and the sum of a 2(x + 8) number and 8

1. 1 Problem Solving • Equation: statement that two algebraic expressions are equal. Expression x– 7 No equal sign Can be evaluated or simplified Equation x– 7=3 Contains equal sign Can be solved

1. 1 Problem Solving with Fractions • Solving Application Problems 1. Read and understand the problem 2. Know what is given and work out a plan to answer what is to be found. 3. Estimate a reasonable answer 4. Solve the problem by using the facts given and your plan

1. 1 Problem Solving with Fractions • Estimating a reasonable answer: which of the following would be a reasonable cost for a man’s shirt? 1. 2. 3. 4. $. 65 $1 $20 $1000

1. 2 Adding and Subtracting Fractions • Adding fractions with the same denominator: • Subtracting fractions with the same denominator:
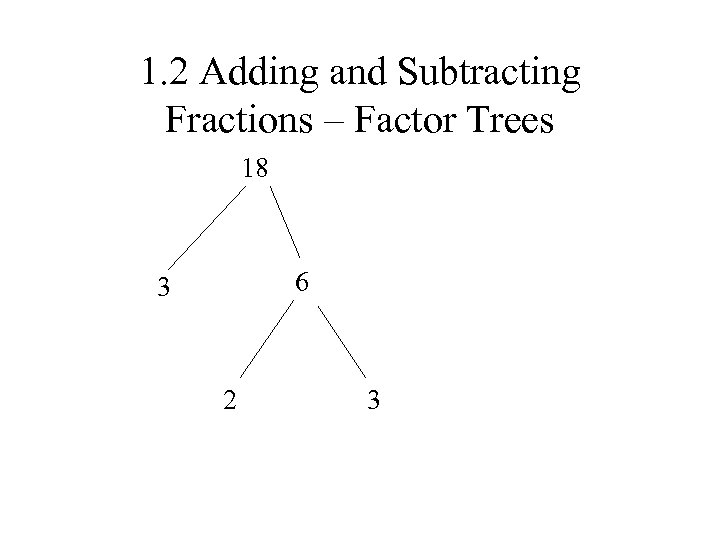
1. 2 Adding and Subtracting Fractions – Factor Trees 18 6 3 2 3

1. 2 Adding and Subtracting Fractions • To add or subtract fractions with different denominators - get a common denominator. • Using the least common denominator: 1. Factor both denominators completely 2. Multiply the largest number of repeats of each prime factor together to get the LCD 3. Multiply the top and bottom of each fraction by the number that produces the LCD in the denominator

1. 2 Adding and Subtracting Fractions – no common factors in denominator • Adding fractions with different denominators: • Subtracting fractions with different denominators:

1. 2 Adding and Subtracting Fractions • Try these:

1. 2 Adding and Subtracting Fractions • Proper fraction – numerator is less than the denominator • Improper fraction - numerator is greater than the denominator • Mixed fraction – sum of a fraction and a whole number

1. 2 Adding and Subtracting Fractions • Converting a mixed fraction to an improper fraction: • Converting an improper fraction to a mixed fraction: Divide 9 into 35:

1. 3 Multiplying and Dividing Fractions • • Multiplying or dividing the numerator (top) and the denominator (bottom) of a fraction by the same number does not change the value of a fraction. Writing a fraction in lowest terms: 1. Factor the top and bottom completely 2. Divide the top and bottom by the greatest common factor

1. 3 Multiplying and Dividing Fractions • Multiplying fractions: • Dividing fractions (multiply by the reciprocal):

1. 3 Multiplying and Dividing Fractions • Try these:

1. 3 Multiplying and Dividing Fractions • Converting decimals fractions: • Converting fractions to decimals:

2. 1 Solving Equations • A linear equation in one variable can be written in the form: Ax + B = 0 • Linear equations are solved by getting “x” by itself on one side of the equation • Addition Property of Equality: if A=B then A+C=B+C • Multiplication Property of Equality: if A=B and C is non-zero, then AC=BC • General rule: Whatever you do to one side of the equation, you must also do it to the other side.

2. 1 Solving Equations • Some equations have more than one term with the same variable. These are called “like terms” • Like terms can be combined by adding the coefficients:

2. 1 Solving Equations • Example of solving an equation:

2. 2 Applications of Equations • 1. 2. 3. 4. 5. Translate the following: The sum of a number and 16 Subtract a number from 5. 4 The product of a number and 9 The quotient of a number and 11 Four-thirds of a number

2. 2 Applications of Equations • When 5 times a number is added to twice the number, the result is 10. Find the number. 1. x is the variable representing the number. 2. Equation: 3. Solve: 4. Check:

2. 3 Formulas • I = PRT • Interest = principal x rate x time • M = P(1 + RT) • Maturity value • G = NP • Gross sales = number of items sold x price per item • S=C+M • Selling price = cost of the item + markup

2. 3 Formulas • Example: Solve for T in the formula: 1. Distribute: 2. Subtract P from both sides 3. Divide by PR

2. 4 Ratios and Proportions • Ratio – quotient of two quantities with the same units Examples: a to b, a: b, or Note: percents are ratios where the second number is always 100:

2. 4 Ratios and Proportions • Proportion – statement that two ratios are equal Examples: Cross multiplication: if then

2. 4 Ratios and Proportions • Solve for x: Cross multiplication: so x = 63

3. 1 Writing Fractions and Decimals as Percents • Write a decimal as a percent by moving the decimal point 2 places to the right and attaching a percent sign: • Example:

3. 1 Writing Fractions as Percents • Write a fraction as a percent by converting the fraction to a decimal and then converting the decimal to a percent: • Example:

3. 1 Writing Fractions and Decimals as Percents • Write a percent as a decimal by moving the decimal point 2 places to the left and removing the percent sign: • Example:

3. 1 Writing Fractions and Decimals as Percents • Write a percent as a fraction by first changing the percent to a decimal then changing the decimal to the fraction and reduce: • Example:

3. 1 Writing Fractions and Decimals as Percents • Write a fractional percent as a decimal by first changing the fractional part to a decimal and leaving the percent sign. Then move the decimal point 2 places to the left and removing the percent sign: • Example:

3. 2 Finding the Part • B = Base – the whole or the total • R = Rate – a number followed by “%” or “percent” • P = Part – the result of multiplying base times rate

3. 2 Finding the Part for a Business Problem • B = Base – sales, R = Rate – sales tax rate, P = Part – sales tax • Example: If the sales tax rate is 5%, what is the sales tax and total sale on $133 of merchandise
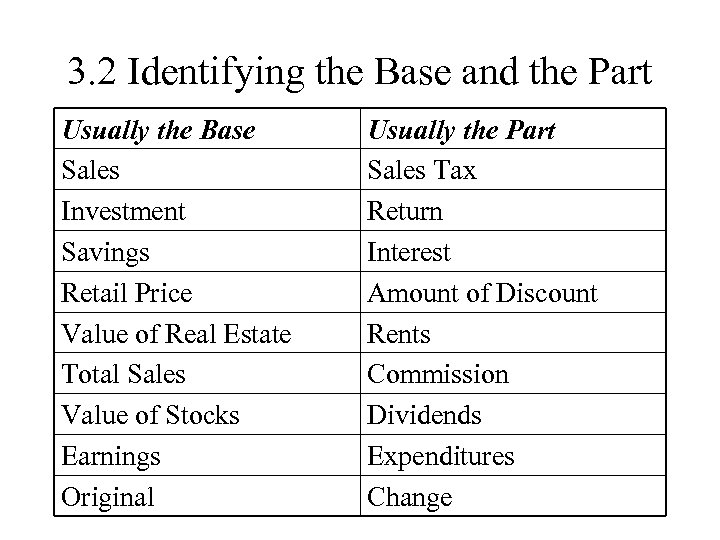
3. 2 Identifying the Base and the Part Usually the Base Sales Investment Savings Retail Price Value of Real Estate Total Sales Value of Stocks Earnings Original Usually the Part Sales Tax Return Interest Amount of Discount Rents Commission Dividends Expenditures Change

3. 3 Finding the Base • Using the Basic Percent Equation to solve for Base: 22. 5 is 30% of _____

3. 3 Finding the Base • Finding sales when sales tax rate is given: The 5% sales tax collected by a store was $380. What was the total amount of sales?

3. 3 Finding the Base • Finding the amount of an investment: The yearly maintenance cost of an apartment is 2½% of its value. If maintenance is $37, 000 per year, what is the value of the apartment complex?

3. 3 Finding the Base • Finding the base if rate and part are different quantities: United Hospital finds that 25% of its employees are men and 720 are women. What is the total number of employees? First – if 25% are men, then the percent of women = 100 -25 = 75%

3. 4 Finding the Rate • Using the percent equation to solve for rate: 45 is what percent of 180? Note: Rate is always expressed as a percent

3. 4 Finding the Rate • Finding rate of return when the amount of return and the investment are known: $3400 is invested in a new computer yielding additional income of $1700. What is the rate of return?

3. 4 Finding the Rate • Solving for the percent remaining: A car is expected to last 10 years before it needs replacement. If the car is 7 years old, what percent of the car’s life remains? To find the number of years remaining subtract 7 from 10 to get 3 years left.

3. 4 Finding the Rate • Find the percent of increase/decrease: Sales of digital cameras went from $40, 000 to $100, 000. Find the percent increase. Increase = $100, 000 - $40, 000 = $60, 000

3. 5 Increase and Decrease Problems • Increase Problem: Original + Increase = New value (base) (part) • Decrease Problem: Original - Decrease = New value (base) (part)

3. 5 Increase and Decrease Problems • The value of a house is $143, 000 this year. That is 10% more than last year’s value. What was the value of the home last year? Last year’s value + 10% of last year’s value = this year’s value

3. 5 Increase and Decrease Problems • Finding the base after 2 increases: This year’s production of widgets was 144, 000. It is 20% more than last year’s production which was also 20% more than the previous year’s production. Find the number of widgets produced 2 years ago. To find last year’s # of widgets:

3. 5 Increase and Decrease Problems • Widget problem (continued). To get the # of widgets produced 2 years ago:

3. 5 Increase and Decrease Problems • Decrease problem: Craig paid $450 for an LCD TV set. The price he paid was 10% less than the original price. What was the original price?
f984a533bcb7584f990bfb226807e8c7.ppt