1 1 K 10 K facets






































 1
1
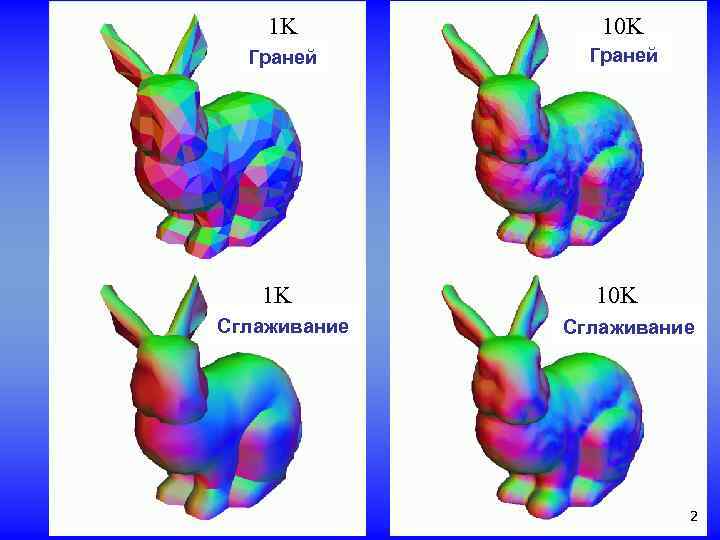
 1 K 10 K facets Граней facets Граней 1 K 10 K smooth Сглаживание smooth Сглаживание 2
1 K 10 K facets Граней facets Граней 1 K 10 K smooth Сглаживание smooth Сглаживание 2
 Параметрические кривые, мотивация 3
Параметрические кривые, мотивация 3
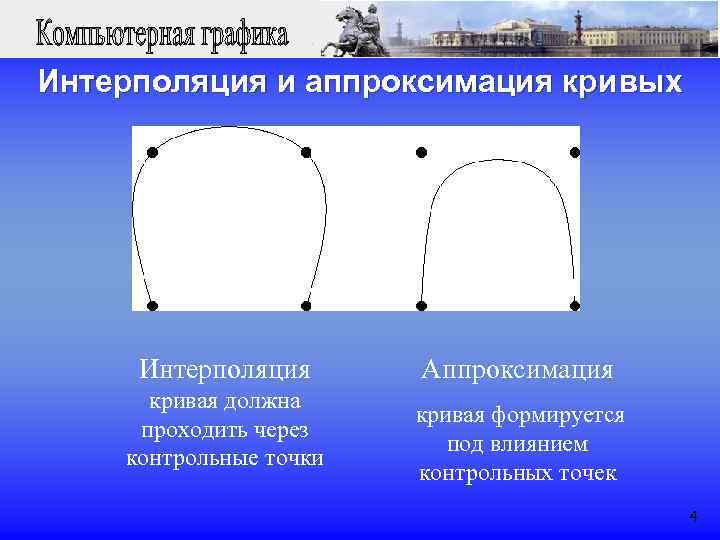
 Интерполяция и аппроксимация кривых Интерполяция Aппроксимация кривая должна кривая формируется проходить через под влиянием контрольные точки контрольных точек 4
Интерполяция и аппроксимация кривых Интерполяция Aппроксимация кривая должна кривая формируется проходить через под влиянием контрольные точки контрольных точек 4
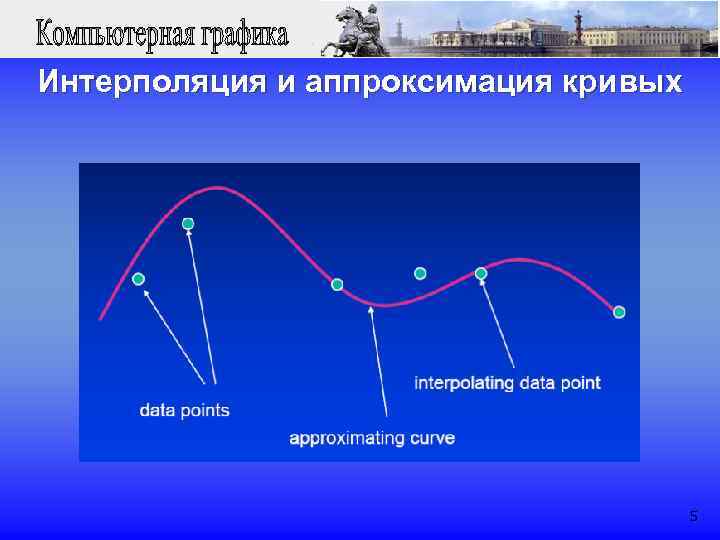
 Интерполяция и аппроксимация кривых 5
Интерполяция и аппроксимация кривых 5
 Задача аппроксимации возникает при замене кривой, заданной уравнениями функций сложной природы (например, с точки зрения скорости расчета ее значений и производных, интегрирования, дифференцирования), другой кривой, близкой к заданной, уравнения которой более простые. Кривую возможно построить путем: n интерполированием или аппроксимацией по точкам; n деформацией кривой (перемещение точки, изменение полинома); n вычислением эквидистанты к заданной кривой; n формированием разомкнутого или замкнутого контура из отрезков или дуг кругов на плоскости; n вычислением конических сечений (эллипс, парабола и т. д. ); n вычислением сечения поверхностей; n соединением кривых. 6
Задача аппроксимации возникает при замене кривой, заданной уравнениями функций сложной природы (например, с точки зрения скорости расчета ее значений и производных, интегрирования, дифференцирования), другой кривой, близкой к заданной, уравнения которой более простые. Кривую возможно построить путем: n интерполированием или аппроксимацией по точкам; n деформацией кривой (перемещение точки, изменение полинома); n вычислением эквидистанты к заданной кривой; n формированием разомкнутого или замкнутого контура из отрезков или дуг кругов на плоскости; n вычислением конических сечений (эллипс, парабола и т. д. ); n вычислением сечения поверхностей; n соединением кривых. 6
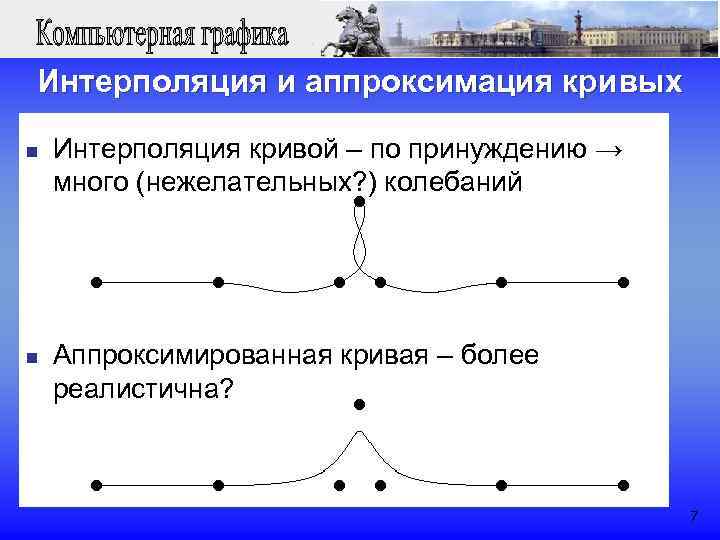
 Интерполяция и аппроксимация кривых n Интерполяция кривой – по принуждению → много (нежелательных? ) колебаний n Аппроксимированная кривая – более реалистична? 7
Интерполяция и аппроксимация кривых n Интерполяция кривой – по принуждению → много (нежелательных? ) колебаний n Аппроксимированная кривая – более реалистична? 7
 Интерполяция и аппроксимация кривых n Требуется аппроксимировать некоторую заданную функцию f(t) конечной суммой n более простых функций так, чтобы выполнилось множество ограничений, наложеных на g(t). Поскольку надо определить n независимых констант C 1, C 2…Cn, на g(t) нужно наложить по меньшей мере n ограничений. n Обычно ограничения на g(t) выбираются такими, чтобы g(t) была «хорошим» приближением функции f(t). n Что такое «хорошее» приближение? 8
Интерполяция и аппроксимация кривых n Требуется аппроксимировать некоторую заданную функцию f(t) конечной суммой n более простых функций так, чтобы выполнилось множество ограничений, наложеных на g(t). Поскольку надо определить n независимых констант C 1, C 2…Cn, на g(t) нужно наложить по меньшей мере n ограничений. n Обычно ограничения на g(t) выбираются такими, чтобы g(t) была «хорошим» приближением функции f(t). n Что такое «хорошее» приближение? 8
 Интерполяционные ограничения В теории аппроксимации часто встречаются следующие ограничения: n 1) интерполяционные ограничения Эти функции должны иметь одинаковые значения в выделеных точках. n 2) смесь интерполяционных ограничений и ограничений гладкости а) б) в) т. е. g(t) дважды непрерывно дифференцируема 3) условия ортогональности В машинной графике нас интересует не качество аппроксимации, измеряемое, например, оценкой ошибки аппроксимации, а свойство, выражаемое через внешний вид кривой или поверхности. Еще это назвают свойством формы. 9
Интерполяционные ограничения В теории аппроксимации часто встречаются следующие ограничения: n 1) интерполяционные ограничения Эти функции должны иметь одинаковые значения в выделеных точках. n 2) смесь интерполяционных ограничений и ограничений гладкости а) б) в) т. е. g(t) дважды непрерывно дифференцируема 3) условия ортогональности В машинной графике нас интересует не качество аппроксимации, измеряемое, например, оценкой ошибки аппроксимации, а свойство, выражаемое через внешний вид кривой или поверхности. Еще это назвают свойством формы. 9
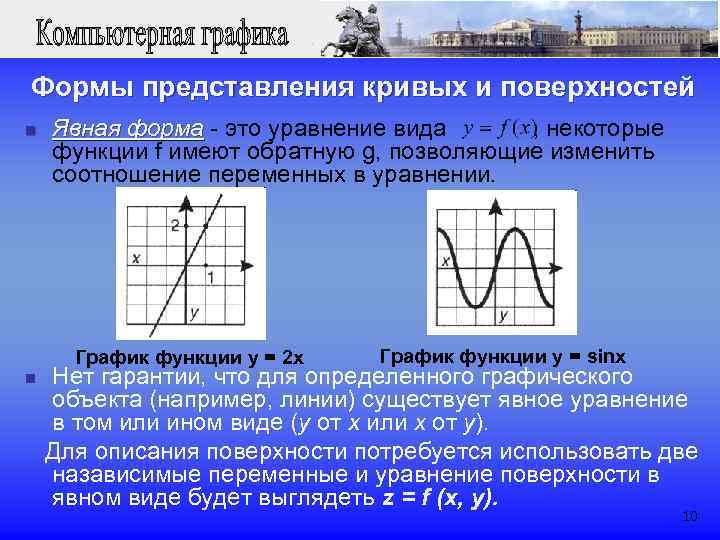
 Формы представления кривых и поверхностей n Явная форма - это уравнение вида , некоторые форма функции f имеют обратную g, позволяющие изменить соотношение переменных в уравнении. График функции у = 2 х График функции у = sinx n Нет гарантии, что для определенного графического объекта (например, линии) существует явное уравнение в том или ином виде (y от x или x от y). Для описания поверхности потребуется использовать две назависимые переменные и уравнение поверхности в явном виде будет выглядеть z = f (x, y). 10
Формы представления кривых и поверхностей n Явная форма - это уравнение вида , некоторые форма функции f имеют обратную g, позволяющие изменить соотношение переменных в уравнении. График функции у = 2 х График функции у = sinx n Нет гарантии, что для определенного графического объекта (например, линии) существует явное уравнение в том или ином виде (y от x или x от y). Для описания поверхности потребуется использовать две назависимые переменные и уравнение поверхности в явном виде будет выглядеть z = f (x, y). 10
 Формы представления кривых и поверхностей n Невная форма. Большинство кривых и поверхностей, с форма которыми приходится работать на практике, можно описать с помощью уравнений в неявной форме Неявная форма для прямой и окружности с центром в начале координат: ìax + by + c = 0 í 2 x + y -R = 0 2 2 î 11
Формы представления кривых и поверхностей n Невная форма. Большинство кривых и поверхностей, с форма которыми приходится работать на практике, можно описать с помощью уравнений в неявной форме Неявная форма для прямой и окружности с центром в начале координат: ìax + by + c = 0 í 2 x + y -R = 0 2 2 î 11
 Параметрические кривые n В параметрической форме каждая координата точки, принадлежащая кривой представляется функцией независимой переменной u, которая называется параметром этой кривой. x =x t +(1 -t)x 0 1 Параметрическое представление для линии: y =y 0 t +(1 -t)y 1 z =z 0 t +(1 -t)z 1 n В трехмерном пространстве кривая описывается системой из трех параметрических уравнений x = x(u), y = y(u), z = z(u) Рассмотрим уравнения кривой в виде где Полиномиальная параметрическая кривая степени n имеет вид 12
Параметрические кривые n В параметрической форме каждая координата точки, принадлежащая кривой представляется функцией независимой переменной u, которая называется параметром этой кривой. x =x t +(1 -t)x 0 1 Параметрическое представление для линии: y =y 0 t +(1 -t)y 1 z =z 0 t +(1 -t)z 1 n В трехмерном пространстве кривая описывается системой из трех параметрических уравнений x = x(u), y = y(u), z = z(u) Рассмотрим уравнения кривой в виде где Полиномиальная параметрическая кривая степени n имеет вид 12
 Почему параметрические кривые? Остановимся на полиномиальной форме, то есть все функции параметра u при описании кривых и параметров u и v при описании поверхностей являются полиномами. Основные доводы в пользу использования параметрического полиномиального представления n Возможность локального контроля формы n Гладкость и непрерывност в математическом смысле n возможность математического вычисления производных n Устойчивость к малым воздействиям (возмущениям) n Возможность использовать простые и значительно высокоскоростные методы закраски 13
Почему параметрические кривые? Остановимся на полиномиальной форме, то есть все функции параметра u при описании кривых и параметров u и v при описании поверхностей являются полиномами. Основные доводы в пользу использования параметрического полиномиального представления n Возможность локального контроля формы n Гладкость и непрерывност в математическом смысле n возможность математического вычисления производных n Устойчивость к малым воздействиям (возмущениям) n Возможность использовать простые и значительно высокоскоростные методы закраски 13
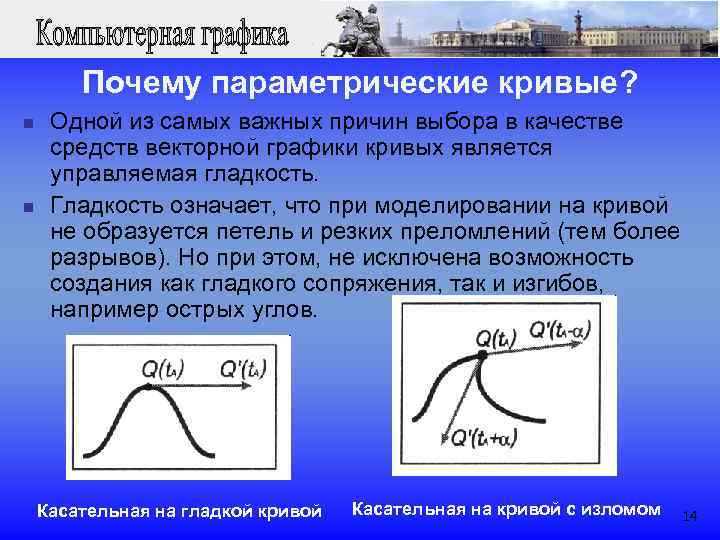
 Почему параметрические кривые? n Одной из самых важных причин выбора в качестве средств векторной графики кривых является управляемая гладкость. n Гладкость означает, что при моделировании на кривой не образуется петель и резких преломлений (тем более разрывов). Но при этом, не исключена возможность создания как гладкого сопряжения, так и изгибов, например острых углов. Касательная на гладкой кривой Касательная на кривой с изломом 14
Почему параметрические кривые? n Одной из самых важных причин выбора в качестве средств векторной графики кривых является управляемая гладкость. n Гладкость означает, что при моделировании на кривой не образуется петель и резких преломлений (тем более разрывов). Но при этом, не исключена возможность создания как гладкого сопряжения, так и изгибов, например острых углов. Касательная на гладкой кривой Касательная на кривой с изломом 14
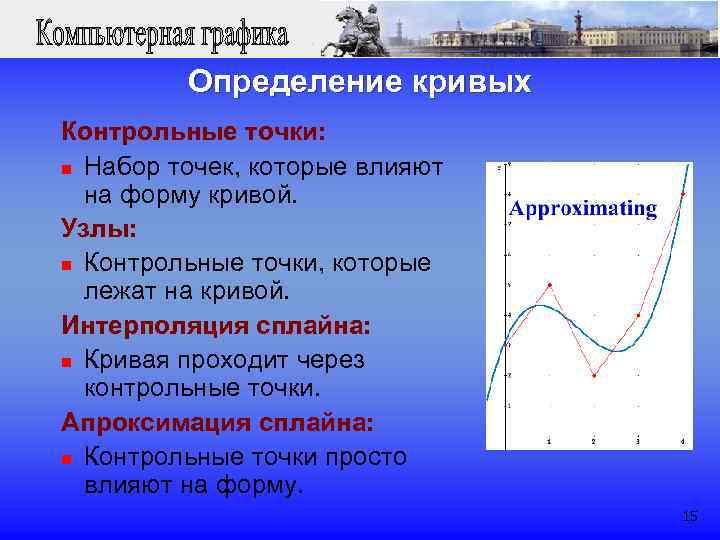
 Определение кривых Контрольные точки: n Набор точек, которые влияют на форму кривой. Узлы: n Контрольные точки, которые лежат на кривой. Интерполяция сплайна: n Кривая проходит через контрольные точки. Апроксимация сплайна: n Контрольные точки просто влияют на форму. 15
Определение кривых Контрольные точки: n Набор точек, которые влияют на форму кривой. Узлы: n Контрольные точки, которые лежат на кривой. Интерполяция сплайна: n Кривая проходит через контрольные точки. Апроксимация сплайна: n Контрольные точки просто влияют на форму. 15
 Геометрическая непрерывность n Непрерывность G 0 n у кривой/поверхности нет никаких разрывов/промежутков/ отверстий n При стыковке по уровню G 0 - непрерывность по координатам n Непрерывность G 1 n 1 -ая производная кривой/поверхности непрерывна n "кажется гладкой, никакие фасеток" n Непрерывность G 2 n кривые/поверхности 2 -ая производная непрерывна Фактически важно для затенения 16
Геометрическая непрерывность n Непрерывность G 0 n у кривой/поверхности нет никаких разрывов/промежутков/ отверстий n При стыковке по уровню G 0 - непрерывность по координатам n Непрерывность G 1 n 1 -ая производная кривой/поверхности непрерывна n "кажется гладкой, никакие фасеток" n Непрерывность G 2 n кривые/поверхности 2 -ая производная непрерывна Фактически важно для затенения 16
 Пример n Вся история параметрических сплайнов связана с получением их коэффициентов. n Как мы это делаем, удовлетворяя ограничения, установленные узлами и условиями непрерывности, - то, что классифицирует систему сплайна и отличает различные системы. n Пример: Кубические Сплайны Эрмита (Hermite) 17
Пример n Вся история параметрических сплайнов связана с получением их коэффициентов. n Как мы это делаем, удовлетворяя ограничения, установленные узлами и условиями непрерывности, - то, что классифицирует систему сплайна и отличает различные системы. n Пример: Кубические Сплайны Эрмита (Hermite) 17
 Параметрические Полиномиальные Кривые n Если N=M=L, нам нужно определить 3(N+1) коэффициентов n Чтобы получить непрерывность C 2, функции должны иметь по крайней мере степень 3. Это - также самая низкая степень для описания неплоской кривой. n Кубическая кривая имеет 4 степени свободы и может управлять 4 параметрами. n Полиномиалы использования: x (u) степени k - функция от u. - y (u) и z (u) подобны, и каждый управляется независимо (вот почему с параметрической формой легче обращаться чем неявной формой). Это: 18
Параметрические Полиномиальные Кривые n Если N=M=L, нам нужно определить 3(N+1) коэффициентов n Чтобы получить непрерывность C 2, функции должны иметь по крайней мере степень 3. Это - также самая низкая степень для описания неплоской кривой. n Кубическая кривая имеет 4 степени свободы и может управлять 4 параметрами. n Полиномиалы использования: x (u) степени k - функция от u. - y (u) и z (u) подобны, и каждый управляется независимо (вот почему с параметрической формой легче обращаться чем неявной формой). Это: 18
 n Сегодня в компьютерной графике параметрические и кубические кривые третьего порядка называют сплайнами. В тоже время сплайн можно разделить на два класса: n 1. кривые, имеющие непрерывные значения функции и ее первой производной; n 2. кривые для которых непрерывна сама функция и ее первая и вторая производные. В первую группу относятся функции, которые проходят через заданные точки (заданные пользователем). Для второго класса функция проходит рядом с управляющими (контрольными) точками. n Примеры: К первому классу относятся функции заданные формой Безье, Эрмита, Кейтмула- Рома; Ко второму классу относятся В-сплайны. 19 Рома
n Сегодня в компьютерной графике параметрические и кубические кривые третьего порядка называют сплайнами. В тоже время сплайн можно разделить на два класса: n 1. кривые, имеющие непрерывные значения функции и ее первой производной; n 2. кривые для которых непрерывна сама функция и ее первая и вторая производные. В первую группу относятся функции, которые проходят через заданные точки (заданные пользователем). Для второго класса функция проходит рядом с управляющими (контрольными) точками. n Примеры: К первому классу относятся функции заданные формой Безье, Эрмита, Кейтмула- Рома; Ко второму классу относятся В-сплайны. 19 Рома
 Сплайны n сплайн - параметрическая кривая, определенная контрольными точками n термин "сплайн" идет от инженерного рисования, где сплайн был частью гибкого прута, используемого, чтобы нарисовать гладкие кривые n контрольные точки настраиваются пользователем, чтобы управлять формой кривой 20
Сплайны n сплайн - параметрическая кривая, определенная контрольными точками n термин "сплайн" идет от инженерного рисования, где сплайн был частью гибкого прута, используемого, чтобы нарисовать гладкие кривые n контрольные точки настраиваются пользователем, чтобы управлять формой кривой 20
 Сплайны n чертежник использовал 'уток (ducks) ' и гибкие полосы (spline - упругая рейка ), чтобы вытянуть кривые n деревянные сплайны имеют непрерывность второго заказа, проходят через контрольные a duck (weight) точки ducks trace out curve 21
Сплайны n чертежник использовал 'уток (ducks) ' и гибкие полосы (spline - упругая рейка ), чтобы вытянуть кривые n деревянные сплайны имеют непрерывность второго заказа, проходят через контрольные a duck (weight) точки ducks trace out curve 21
 Кривая Эрмита n Кривая Эрмита - кривая, для которой пользователь обеспечивает : n конечные точки кривой n параметрические производные кривой в конечных точках n параметрические производные - dx/dt, dy/dt, dz/dt n больше производных требовалось бы для кривых более высоких степеней 22
Кривая Эрмита n Кривая Эрмита - кривая, для которой пользователь обеспечивает : n конечные точки кривой n параметрические производные кривой в конечных точках n параметрические производные - dx/dt, dy/dt, dz/dt n больше производных требовалось бы для кривых более высоких степеней 22
 Кривая Эрмита(2) n 4 степени свободы, 2 в каждом конце, чтобы управлять C 0 и непрерывностью C 1 в каждом конце. n Полиномиал может быть определен положением, и производной в каждой конечной точке кривой. n Определим: р = Р (t) в термина Р(t) и P/ (t) Определим коэффициенты 23
Кривая Эрмита(2) n 4 степени свободы, 2 в каждом конце, чтобы управлять C 0 и непрерывностью C 1 в каждом конце. n Полиномиал может быть определен положением, и производной в каждой конечной точке кривой. n Определим: р = Р (t) в термина Р(t) и P/ (t) Определим коэффициенты 23
 Кривая Эрмита(3) Для кривой Эрмита должны существовать некоторые константы a 3, a 2, a 1, a 0 И они могут быть вычислены из контрольных точек, но как? n Мы имеем утверждения: n Кривая должна проходить через x 0 когда t=0 n производная должна быть x’ 0 когда t=0 n Кривая должна проходить через x 1 когда t=1 n производная должна быть x’ 1 когда t=1 24
Кривая Эрмита(3) Для кривой Эрмита должны существовать некоторые константы a 3, a 2, a 1, a 0 И они могут быть вычислены из контрольных точек, но как? n Мы имеем утверждения: n Кривая должна проходить через x 0 когда t=0 n производная должна быть x’ 0 когда t=0 n Кривая должна проходить через x 1 когда t=1 n производная должна быть x’ 1 когда t=1 24
 Матрица Эрмита - MH Проистекающий полиномиал может быть выражен в матричной форме: X(t) = t. TMHq (q – геометрический вектор контроля) 25
Матрица Эрмита - MH Проистекающий полиномиал может быть выражен в матричной форме: X(t) = t. TMHq (q – геометрический вектор контроля) 25
 Матрица Эрмита - MH Проистекающий полиномиал может быть выражен в матричной форме: X(t) = t. TMHq (q – геометрический вектор контроля) Мы можем теперь определить параметрический полиномиал для каждой координаты, независимо, то есть, X(t), Y(t) и Z(t) 26
Матрица Эрмита - MH Проистекающий полиномиал может быть выражен в матричной форме: X(t) = t. TMHq (q – геометрический вектор контроля) Мы можем теперь определить параметрический полиномиал для каждой координаты, независимо, то есть, X(t), Y(t) и Z(t) 26
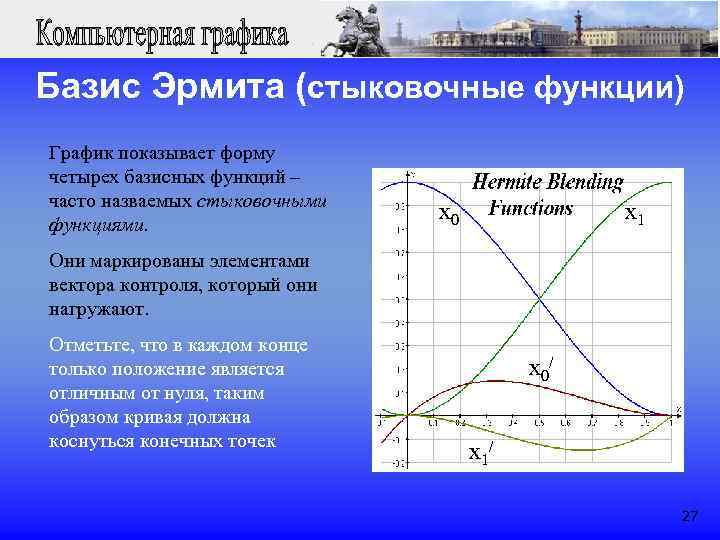
 Базис Эрмита (стыковочные функции) График показывает форму четырех базисных функций – часто назваемых стыковочными x 0 x 1 функциями. Они маркированы элементами вектора контроля, который они нагружают. Отметьте, что в каждом конце только положение является x 0/ отличным от нуля, таким образом кривая должна коснуться конечных точек x 1/ 27
Базис Эрмита (стыковочные функции) График показывает форму четырех базисных функций – часто назваемых стыковочными x 0 x 1 функциями. Они маркированы элементами вектора контроля, который они нагружают. Отметьте, что в каждом конце только положение является x 0/ отличным от нуля, таким образом кривая должна коснуться конечных точек x 1/ 27
 Кривые Эрмита y(t) Note : Начало слева. x(t) 28
Кривые Эрмита y(t) Note : Начало слева. x(t) 28
 Кривые Эрмита n Две эрмитовых кубические Р 1 кривые, соединенные в точке Р 4. Р 7 Их касательные векторы имеют Р 4 одинаковое направление, но различаются по величине. Свойства n 1) гладкая кривая n 2) проходит через вершины n 3) касательный вектор однозначно определяется через массив вершин n 4) Не лежит в выпуклой оболочке порожденной матрицей образованной вершинами P n 5) Аффинно – инвариантна n 6) При добавлении хотя бы 1 точки вершины возникает необходимость полного пересчета всех параметрических уравнений. n 7) Изменение хотя бы 1 -й вершины | касательной вектора в концевых точках приводит к изменению формы кривой. 29
Кривые Эрмита n Две эрмитовых кубические Р 1 кривые, соединенные в точке Р 4. Р 7 Их касательные векторы имеют Р 4 одинаковое направление, но различаются по величине. Свойства n 1) гладкая кривая n 2) проходит через вершины n 3) касательный вектор однозначно определяется через массив вершин n 4) Не лежит в выпуклой оболочке порожденной матрицей образованной вершинами P n 5) Аффинно – инвариантна n 6) При добавлении хотя бы 1 точки вершины возникает необходимость полного пересчета всех параметрических уравнений. n 7) Изменение хотя бы 1 -й вершины | касательной вектора в концевых точках приводит к изменению формы кривой. 29
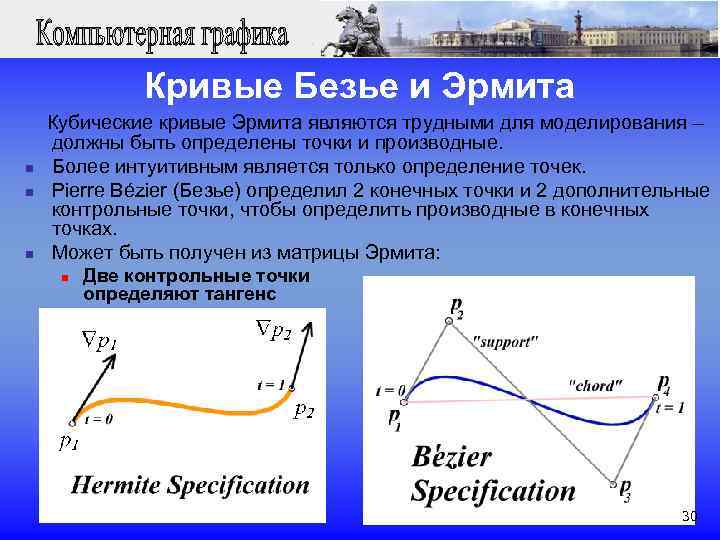
 Кривые Безье и Эрмита Кубические кривые Эрмита являются трудными для моделирования – должны быть определены точки и производные. n Более интуитивным является только определение точек. n Pierre Bézier (Безье) определил 2 конечных точки и 2 дополнительные контрольные точки, чтобы определить производные в конечных точках. n Может быть получен из матрицы Эрмита: n Две контрольные точки определяют тангенс 30
Кривые Безье и Эрмита Кубические кривые Эрмита являются трудными для моделирования – должны быть определены точки и производные. n Более интуитивным является только определение точек. n Pierre Bézier (Безье) определил 2 конечных точки и 2 дополнительные контрольные точки, чтобы определить производные в конечных точках. n Может быть получен из матрицы Эрмита: n Две контрольные точки определяют тангенс 30
 Кривые Безье Метод Безье, который использует аппроксимацию многочленами Бернштейна. Пусть задана совокупность из (n+1) точек которую будем называть ломаной Безье. Кривая Безье, соответствующая этой ломаной, описывается в виде функции параметра t следующим полиномом: где - радиус-вектор точек на кривой, а Jni(t) - аппроксимирующие многочлены Бернштейна, равные n Здесь 0 t 1 и, кроме того, предполагается, что ti=1 при i=0 и t=0. n Ломаная Безье однозначно определяет форму кривой Безье. Изменяя положения вершин ломаной, можно управлять формой соответствующей кривой Безье 31
Кривые Безье Метод Безье, который использует аппроксимацию многочленами Бернштейна. Пусть задана совокупность из (n+1) точек которую будем называть ломаной Безье. Кривая Безье, соответствующая этой ломаной, описывается в виде функции параметра t следующим полиномом: где - радиус-вектор точек на кривой, а Jni(t) - аппроксимирующие многочлены Бернштейна, равные n Здесь 0 t 1 и, кроме того, предполагается, что ti=1 при i=0 и t=0. n Ломаная Безье однозначно определяет форму кривой Безье. Изменяя положения вершин ломаной, можно управлять формой соответствующей кривой Безье 31
 Матрица Безье n Кубическая форма является самой популярной X(t) = t. TMBq (MB – матрица Безье) n При n=4 и r=0, 1, 2, 3 мы получаем: n Аналогично для Y(t) и Z(t) 32
Матрица Безье n Кубическая форма является самой популярной X(t) = t. TMBq (MB – матрица Безье) n При n=4 и r=0, 1, 2, 3 мы получаем: n Аналогично для Y(t) и Z(t) 32
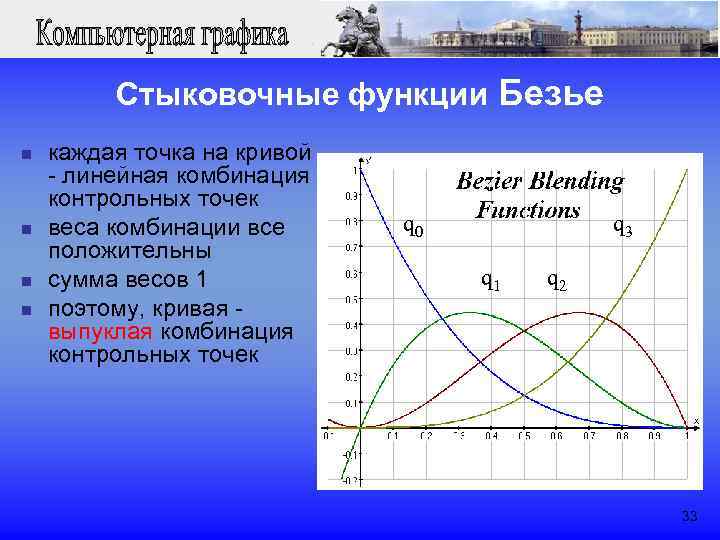
 Стыковочные функции Безье n каждая точка на кривой - линейная комбинация контрольных точек n веса комбинации все q 0 q 3 положительны n сумма весов 1 q 1 q 2 n поэтому, кривая - выпуклая комбинация контрольных точек 33
Стыковочные функции Безье n каждая точка на кривой - линейная комбинация контрольных точек n веса комбинации все q 0 q 3 положительны n сумма весов 1 q 1 q 2 n поэтому, кривая - выпуклая комбинация контрольных точек 33
 n Если необходима более гибкая кривая Безье, увеличивается количество пределяющих точек и степень полинома. Для каждой точки на кривой Безье с n определяющими вершинами многоугольника B 0, . . . , Вn та же самая точка на новой кривой Безье с n + 1 определяющими вершинами B 0*, . . . , Вп+1* задается в виде Кубическая кривая Безье для n=4 задается в виде P(t) = (1 - t)3 B 0 + 3 t(l – t)2 B 1 + 3*t 2 (1 - t)B 2 + t 3 B 3, 0
n Если необходима более гибкая кривая Безье, увеличивается количество пределяющих точек и степень полинома. Для каждой точки на кривой Безье с n определяющими вершинами многоугольника B 0, . . . , Вn та же самая точка на новой кривой Безье с n + 1 определяющими вершинами B 0*, . . . , Вп+1* задается в виде Кубическая кривая Безье для n=4 задается в виде P(t) = (1 - t)3 B 0 + 3 t(l – t)2 B 1 + 3*t 2 (1 - t)B 2 + t 3 B 3, 0
 Пример кривых Безье 35
Пример кривых Безье 35
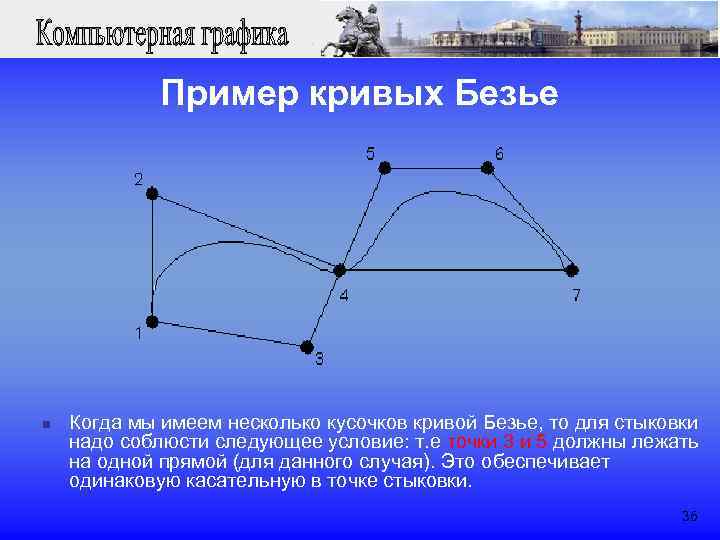
 Пример кривых Безье n Когда мы имеем несколько кусочков кривой Безье, то для стыковки надо соблюсти следующее условие: т. е точки 3 и 5 должны лежать на одной прямой (для данного случая). Это обеспечивает одинаковую касательную в точке стыковки. 36
Пример кривых Безье n Когда мы имеем несколько кусочков кривой Безье, то для стыковки надо соблюсти следующее условие: т. е точки 3 и 5 должны лежать на одной прямой (для данного случая). Это обеспечивает одинаковую касательную в точке стыковки. 36
 Пример кривых Безье 37
Пример кривых Безье 37
 n Элементарные кубические кривые Безье, порожденные набором из четырех точек, которые различаются нумерацией 3 1 2 1 4 1 4 2 2 38
n Элементарные кубические кривые Безье, порожденные набором из четырех точек, которые различаются нумерацией 3 1 2 1 4 1 4 2 2 38
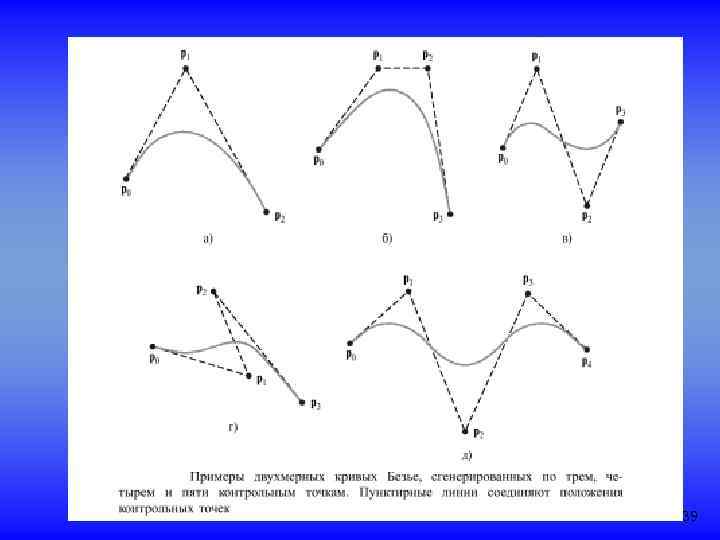
 39
39
 Построение кривой Bezier n шаг 1: найдите середины линий, присоединяющихся к контрольным вершинам. назовите их M 01, M 12, M 23 P 1 M 12 P 2 M 01 M 23 P 0 P 3 40
Построение кривой Bezier n шаг 1: найдите середины линий, присоединяющихся к контрольным вершинам. назовите их M 01, M 12, M 23 P 1 M 12 P 2 M 01 M 23 P 0 P 3 40
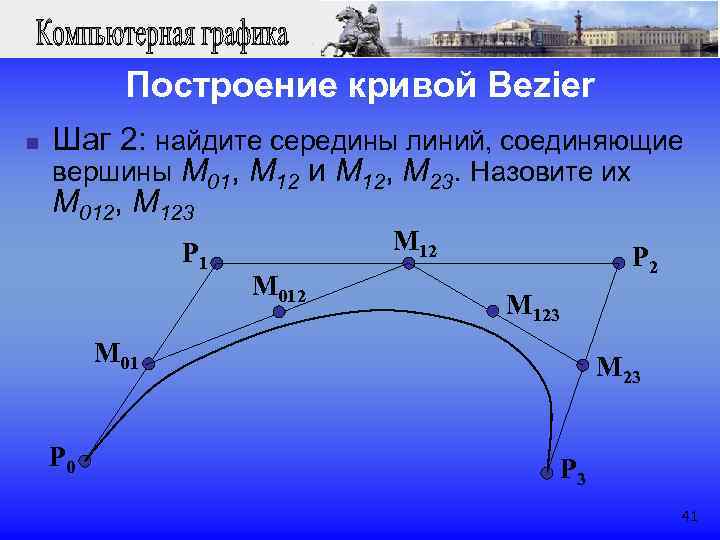
 Построение кривой Bezier n Шаг 2: найдите середины линий, соединяющие вершины M 01, M 12 и M 12, M 23. Назовите их M 012, M 123 P 1 M 12 P 2 M 012 M 123 M 01 M 23 P 0 P 3 41
Построение кривой Bezier n Шаг 2: найдите середины линий, соединяющие вершины M 01, M 12 и M 12, M 23. Назовите их M 012, M 123 P 1 M 12 P 2 M 012 M 123 M 01 M 23 P 0 P 3 41
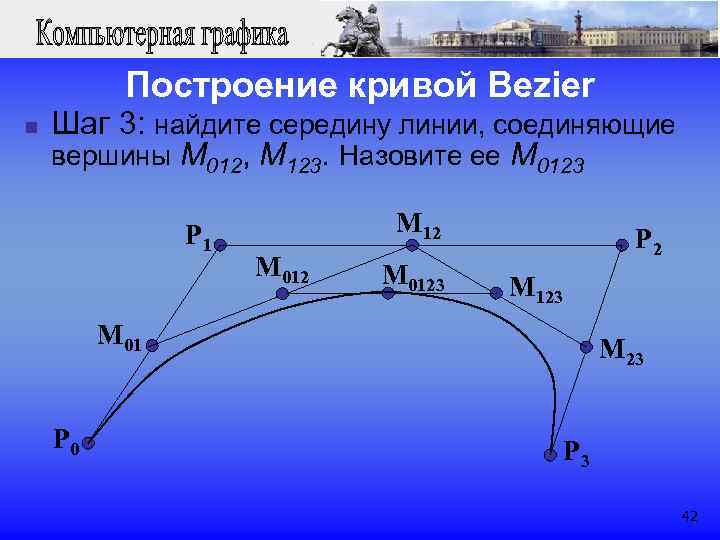
 Построение кривой Bezier n Шаг 3: найдите середину линии, соединяющие вершины M 012, M 123. Назовите ее M 0123 P 1 M 12 P 2 M 0123 M 123 M 01 M 23 P 0 P 3 42
Построение кривой Bezier n Шаг 3: найдите середину линии, соединяющие вершины M 012, M 123. Назовите ее M 0123 P 1 M 12 P 2 M 0123 M 123 M 01 M 23 P 0 P 3 42
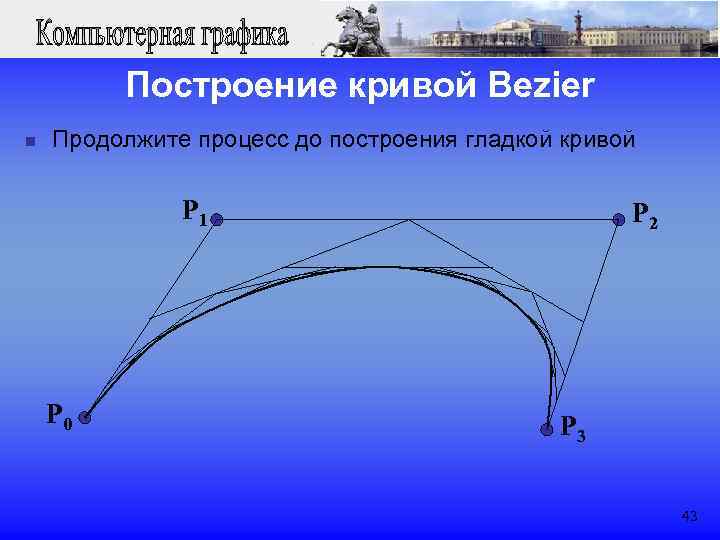
 Построение кривой Bezier n Продолжите процесс до построения гладкой кривой P 1 P 2 P 0 P 3 43
Построение кривой Bezier n Продолжите процесс до построения гладкой кривой P 1 P 2 P 0 P 3 43
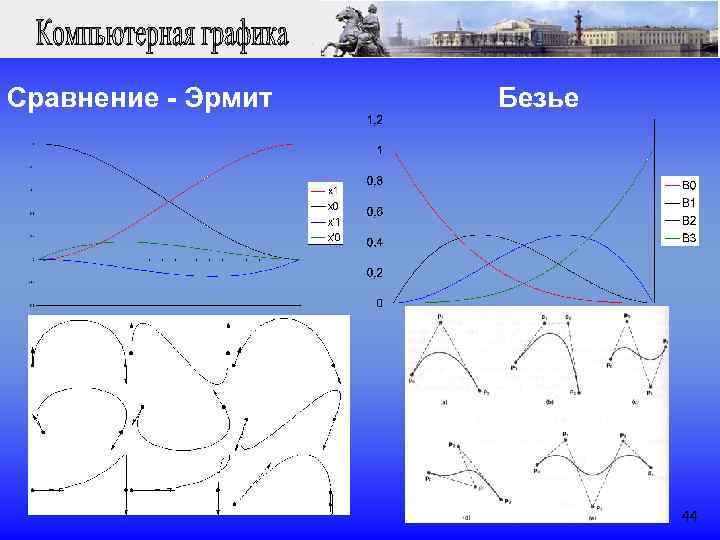
 Сравнение - Эрмит Безье 44
Сравнение - Эрмит Безье 44
 n Свойства кривых Безье 1. Гладкая кривая 2. Лежит в выпуклой оболочке 3. Ассиметрично сохраняет форму при перемене порядка вершин в массиве вершин. 4. Аффинно – инвариантна 5. Повторяет опорную ломаную 6. Если точки лежат на одной прямой (горизонтальной| вертикальной), то кривая совпадает с ломаной. 7. Степень функционального многочлена напрямую связана с количеством вершин (на 1 больше) и растет при его увеличении 8. При добавлении хотя бы одной вершины возникает необходимость пересчета параметрического уравнения кривой. 9. Изменение 1 й вершины приводит к заметному изменению кривой Безье. 10. Т. к. поведение кривой Безье определяется нетолько набором вершин, но и параметрическими коэфициентами, их называют весовыми коэффициентами ( параметры формы) 11. Формой кривой Безье можно управлять изменяя весовые коэффициэнты| параметрические формы. 45
n Свойства кривых Безье 1. Гладкая кривая 2. Лежит в выпуклой оболочке 3. Ассиметрично сохраняет форму при перемене порядка вершин в массиве вершин. 4. Аффинно – инвариантна 5. Повторяет опорную ломаную 6. Если точки лежат на одной прямой (горизонтальной| вертикальной), то кривая совпадает с ломаной. 7. Степень функционального многочлена напрямую связана с количеством вершин (на 1 больше) и растет при его увеличении 8. При добавлении хотя бы одной вершины возникает необходимость пересчета параметрического уравнения кривой. 9. Изменение 1 й вершины приводит к заметному изменению кривой Безье. 10. Т. к. поведение кривой Безье определяется нетолько набором вершин, но и параметрическими коэфициентами, их называют весовыми коэффициентами ( параметры формы) 11. Формой кривой Безье можно управлять изменяя весовые коэффициэнты| параметрические формы. 45
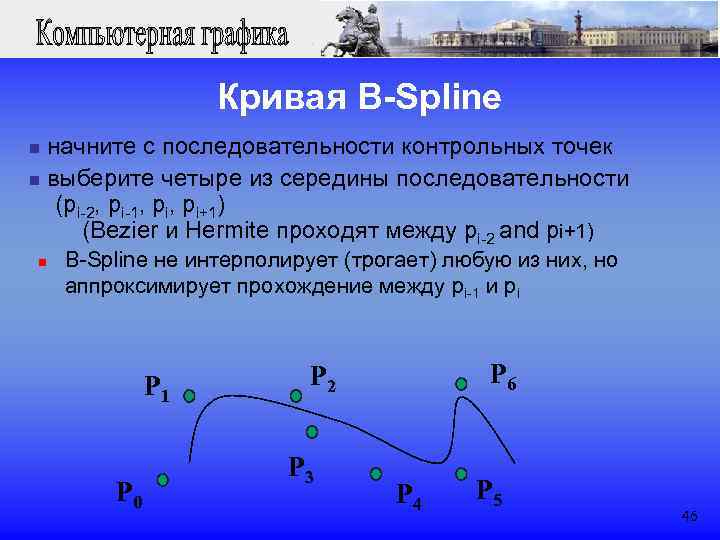
 Кривая B-Spline n начните с последовательности контрольных точек n выберите четыре из середины последовательности (pi-2, pi-1, pi+1) (Bezier и Hermite проходят между pi-2 and pi+1) n B-Spline не интерполирует (трогает) любую из них, но аппроксимирует прохождение между pi-1 и pi P 1 P 2 P 6 P 3 P 0 P 4 P 5 46
Кривая B-Spline n начните с последовательности контрольных точек n выберите четыре из середины последовательности (pi-2, pi-1, pi+1) (Bezier и Hermite проходят между pi-2 and pi+1) n B-Spline не интерполирует (трогает) любую из них, но аппроксимирует прохождение между pi-1 и pi P 1 P 2 P 6 P 3 P 0 P 4 P 5 46
 Матрица B-сплайна 47
Матрица B-сплайна 47
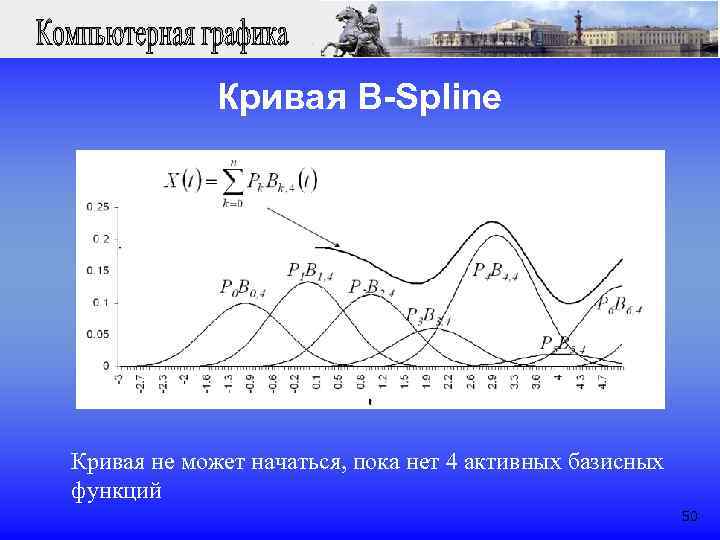
 Кривая B-Spline n Кривая: n n - общее количество контрольных точек n d - порядок кривых, 2 d n+1 n Bk, d - однородные стыковочные функции B-сплайна степени d-1 n Pk - контрольные точки n Каждая Bk, d только отличны от нуля для маленького диапазона значений t, таким образом кривая имеет локальный контроль 48
Кривая B-Spline n Кривая: n n - общее количество контрольных точек n d - порядок кривых, 2 d n+1 n Bk, d - однородные стыковочные функции B-сплайна степени d-1 n Pk - контрольные точки n Каждая Bk, d только отличны от нуля для маленького диапазона значений t, таким образом кривая имеет локальный контроль 48
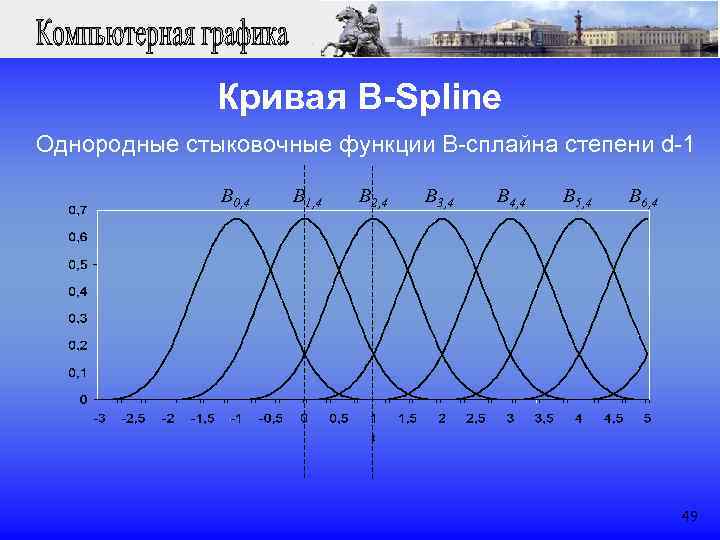
 Кривая B-Spline Однородные стыковочные функции B-сплайна степени d-1 B 0, 4 B 1, 4 B 2, 4 B 3, 4 B 4, 4 B 5, 4 B 6, 4 49
Кривая B-Spline Однородные стыковочные функции B-сплайна степени d-1 B 0, 4 B 1, 4 B 2, 4 B 3, 4 B 4, 4 B 5, 4 B 6, 4 49
 Кривая B-Spline Кривая не может начаться, пока нет 4 активных базисных функций 50
Кривая B-Spline Кривая не может начаться, пока нет 4 активных базисных функций 50
 B-Spline n безусловно самый популярный используемый сплайн n C 0, C 1, и C 2 непрерывность 51
B-Spline n безусловно самый популярный используемый сплайн n C 0, C 1, и C 2 непрерывность 51
 Непрерывность • Параметрическая непрерывность (C): – Непрерывность координационных функций • Геометрическая непрерывность (G): – Непрерывность кривой непосредственно • Никакая форма непрерывности не гарантирует другой: – Может быть C 1, но не G 1, когда p (t) приходит в остановку – Может быть G 1, но не C 1, когда вектор тангенса изменяет резко длину 52
Непрерывность • Параметрическая непрерывность (C): – Непрерывность координационных функций • Геометрическая непрерывность (G): – Непрерывность кривой непосредственно • Никакая форма непрерывности не гарантирует другой: – Может быть C 1, но не G 1, когда p (t) приходит в остановку – Может быть G 1, но не C 1, когда вектор тангенса изменяет резко длину 52
 n Пример непрерывности B-сплайна P 0 P 2 Первый узел, показанный с 4 контрольными точками, и их выпуклой оболочкой. P 1 P 3 53
n Пример непрерывности B-сплайна P 0 P 2 Первый узел, показанный с 4 контрольными точками, и их выпуклой оболочкой. P 1 P 3 53
 n Пример непрерывности B-сплайна P 0 P 2 P 4 Два первых сегмента кривой показанны с их соответствующими выпуклыми оболочками. Центральный узел должен лежать на пересечении 2 выпуклых оболочек. P 1 P 3 54
n Пример непрерывности B-сплайна P 0 P 2 P 4 Два первых сегмента кривой показанны с их соответствующими выпуклыми оболочками. Центральный узел должен лежать на пересечении 2 выпуклых оболочек. P 1 P 3 54
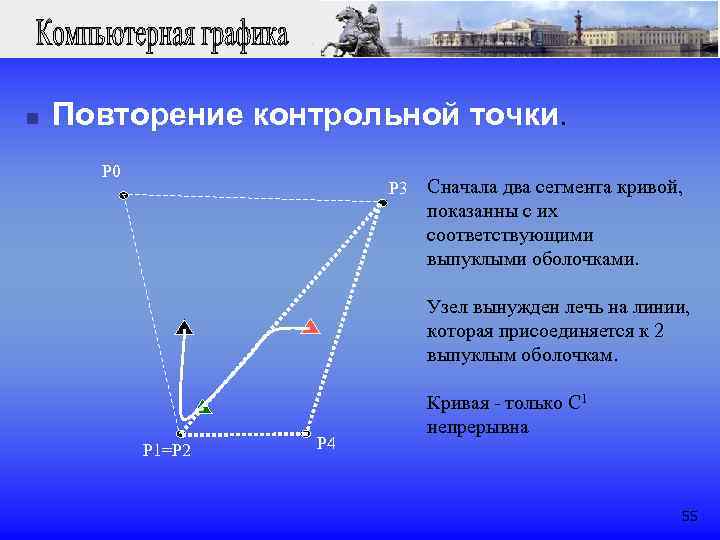
 n Повторение контрольной точки. P 0 P 3 Сначала два сегмента кривой, показанны с их соответствующими выпуклыми оболочками. Узел вынужден лечь на линии, которая присоединяется к 2 выпуклым оболочкам. Кривая - только C 1 непрерывна P 1=P 2 P 4 55
n Повторение контрольной точки. P 0 P 3 Сначала два сегмента кривой, показанны с их соответствующими выпуклыми оболочками. Узел вынужден лечь на линии, которая присоединяется к 2 выпуклым оболочкам. Кривая - только C 1 непрерывна P 1=P 2 P 4 55
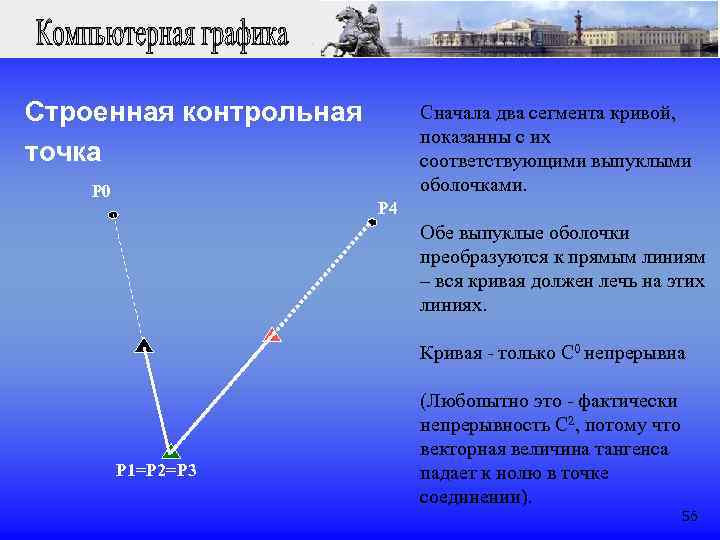
 Строенная контрольная Сначала два сегмента кривой, показанны с их точка соответствующими выпуклыми P 0 оболочками. P 4 Обе выпуклые оболочки преобразуются к прямым линиям – вся кривая должен лечь на этих линиях. Кривая - только C 0 непрерывна (Любопытно это - фактически непрерывность C 2, потому что векторная величина тангенса P 1=P 2=P 3 падает к нолю в точке соединении). 56
Строенная контрольная Сначала два сегмента кривой, показанны с их точка соответствующими выпуклыми P 0 оболочками. P 4 Обе выпуклые оболочки преобразуются к прямым линиям – вся кривая должен лечь на этих линиях. Кривая - только C 0 непрерывна (Любопытно это - фактически непрерывность C 2, потому что векторная величина тангенса P 1=P 2=P 3 падает к нолю в точке соединении). 56
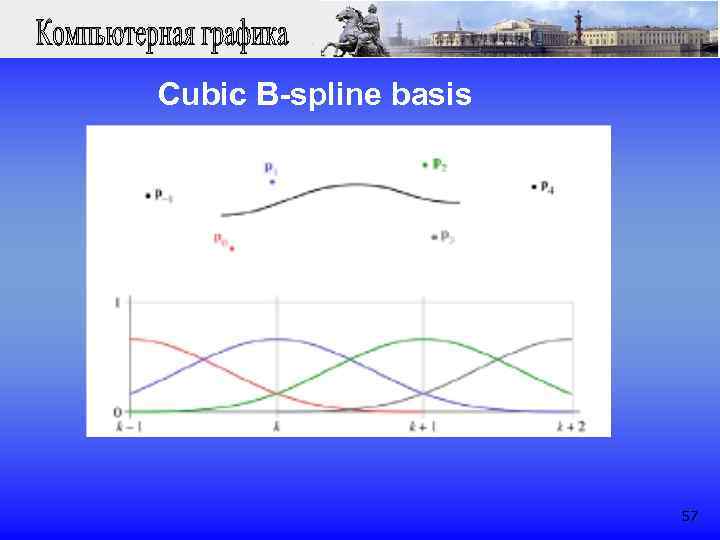
 Cubic B-spline basis 57
Cubic B-spline basis 57
 Переход от B-сплайна к Безье кривых 58
Переход от B-сплайна к Безье кривых 58
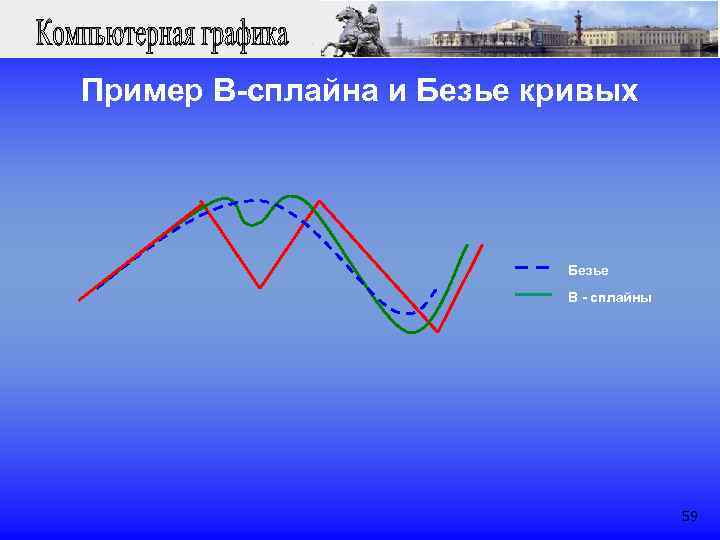
 Пример B-сплайна и Безье кривых Безье В - сплайны 59
Пример B-сплайна и Безье кривых Безье В - сплайны 59
 Свойства B-сплайна 1) гладкая 2) не проходит ни через 1 точку массива 3) лежит в выпуклой оболочке порождаемой этим массивом 4) повторяет опорную ломаную 5) если опорные точки находятся на прямой, то В – сплайн лежит на этой прямой. 6) если опорные точки лежат в одной плоскости ( компланарные), то составная (В- сплайновая) кривая лежит в этой плоскости. 7) изменение одной из вершин приводит только к изменению части кривой 8) При добавлении 1 вершины возникает необходимость пересчета 1 -х элементов кривых (параметрическое уравнение) 9) Аффинно - инвариантна 10) проективно инвариантна ( проективные преобразования не влияют на форму нашей кривой) 11) существуют весовые коэффициенты 60
Свойства B-сплайна 1) гладкая 2) не проходит ни через 1 точку массива 3) лежит в выпуклой оболочке порождаемой этим массивом 4) повторяет опорную ломаную 5) если опорные точки находятся на прямой, то В – сплайн лежит на этой прямой. 6) если опорные точки лежат в одной плоскости ( компланарные), то составная (В- сплайновая) кривая лежит в этой плоскости. 7) изменение одной из вершин приводит только к изменению части кривой 8) При добавлении 1 вершины возникает необходимость пересчета 1 -х элементов кривых (параметрическое уравнение) 9) Аффинно - инвариантна 10) проективно инвариантна ( проективные преобразования не влияют на форму нашей кривой) 11) существуют весовые коэффициенты 60
 Выводы n Каждое из этих представлений оказывается полезным в разных ситуациях. Форма Эрмита пригодна при аппроксимации уже имеющихся поверхностей, когда необходимо добиться как соответствия точек, так и соответствия касательных векторов, в то время как представление в виде В-сплайнов удобно для аппроксимации точек и достижения С(2) –непрерывности. n Формы Безье и В-сплайнов пригодна для работы в интерактивном режиме, так как их геометрические векторы состоят только из точек. Обе эти формы обладают свойством выпуклости оболочки, которое оказывается полезным при изображении кривых. Кривую, первоначально заданную в одной форме, можно преобразовать в другую форму, если записать геометрический вектор первой формы в терминах второй 61
Выводы n Каждое из этих представлений оказывается полезным в разных ситуациях. Форма Эрмита пригодна при аппроксимации уже имеющихся поверхностей, когда необходимо добиться как соответствия точек, так и соответствия касательных векторов, в то время как представление в виде В-сплайнов удобно для аппроксимации точек и достижения С(2) –непрерывности. n Формы Безье и В-сплайнов пригодна для работы в интерактивном режиме, так как их геометрические векторы состоят только из точек. Обе эти формы обладают свойством выпуклости оболочки, которое оказывается полезным при изображении кривых. Кривую, первоначально заданную в одной форме, можно преобразовать в другую форму, если записать геометрический вектор первой формы в терминах второй 61

