1 1 Contratti Forward Lezione 1 1999

1. 1 Contratti Forward Lezione 1 © 1999 di V. M. or J. H. 1

1. 2 Contratto Forward «Agreement to buy or sell “something” in the future» l Accordo per comprare o vendere un’attività ad una certa data futura, per un certo prezzo (p. 1). © 1999 di V. M. or J. H. 2

1. 3 Come Funziona un Contratto Forward – Il «contratto forward» è un accordo tra 2 società sul mercato over the counter (OTC) – Di solito il prezzo del contratto è scelto in modo che il «valore iniziale di mercato» del contratto sia nullo – Pertanto, non c’è alcuno scambio di denaro nel momento in cui il contratto viene stipulato – Il contratto viene «liquidato a scadenza» © 1999 di V. M. or J. H. 3

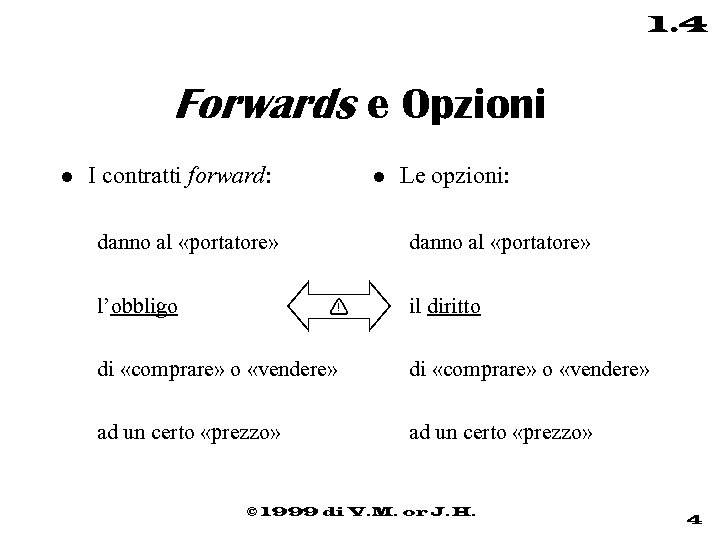1. 4 Forwards e Opzioni l I contratti forward: l danno al «portatore» l’obbligo Le opzioni: danno al «portatore» ! il diritto di «comprare» o «vendere» ad un certo «prezzo» © 1999 di V. M. or J. H. 4

1. 5 Il Prezzo Forward l Il prezzo forward di un contratto è il prezzo di consegna che si applica ad un contratto concluso «adesso» l Il prezzo forward può essere «diverso» per contratti con «diverse» scadenze © 1999 di V. M. or J. H. 5

1. 6 Esempio – 8 maggio 1995: una società entra in un contratto forward lungo per acquistare tra 90 giorni £ 1. 000 a $1, 6056 per sterlina – 6 agosto 1995: il «tasso di cambio spot» della sterlina è pari a $1, 6500 – In base alle «condizioni» contrattuali, la società paga $1. 605. 600 e riceve £ 1. 000 – Il «profitto» della società è pari a $44. 400, dato che le sterline possono essere immediatamente rivendute a $1. 650. 000 © 1999 di V. M. or J. H. 6

1. 7 Posizione Lunga su un Forward – Figura 1. 1 (a) p. 3 prezzo forward o prezzo di consegna? © 1999 di V. M. or J. H. 7

1. 8 Posizione Corta su un Forward – Figura 1. 1 (b) p. 3 © 1999 di V. M. or J. H. 8

1. 9 Terminologia dei Forwards l Prezzo Forward: – prezzo di consegna del giorno di stipula tale da rendere il valore del contratto forward nullo l Prezzo di consegna: – prezzo applicato alla compravendita a termine l Valore del contratto Forward: © 1999 di V. M. or J. H. 9

1. 10 Opportunità di Arbitraggio «You make money without risk» l Condizione favorevole di mercato che consente di ottenere dei guadagni certi da un investimento al più nullo: l Condizione favorevole di mercato che consente di non subire perdite da un investimento autofinanziante: © 1999 di V. M. or J. H. 10

1. 11 Oro: un’ Opportunità di Arbitraggio? l – – – l Si supponga che: il prezzo spot dell’oro sia di $390 il prezzo forward a 1 anno dell’oro sia di $425 il «tasso d’interesse» a 1 anno in dollari sia del 5% annuo C’è un’opportunità di arbitraggio? © 1999 di V. M. or J. H. 11

1. 12 Oro: un’Altra Opportunità di Arbitraggio? l – – – l Si supponga che: il prezzo spot dell’oro sia di $390 il prezzo forward a 1 anno dell’oro sia di $390 il «tasso d’interesse» a 1 anno in dollari sia del 5% annuo C’è un’opportunità di arbitraggio? © 1999 di V. M. or J. H. 12

1. 13 Il Prezzo Forward dell’Oro l l Se il prezzo spot dell’oro è S e il prezzo forward è F, allora, per un contratto consegna dopo T anni, vale la relazione F S 1 r T dove r è il tasso d’interesse privo di rischio (nella valuta interna) Nei nostri esempi T 1 e quindi F $390 1 0, 05 $409, 5 © 1999 di V. M. or J. H. 13

1. 14 L’Esempio dell’Oro – Supponendo che i «costi di immagazzinamento» dell’oro siano nulli, F S 1 r T t dove: F: prezzo forward S: prezzo spot r: tasso d’interesse a T t anni «composto annualmente» – Se r è il tasso a T t anni «composto continuamente» F Ser T t (3. 5) p. 51 © 1999 di V. M. or J. H. 14

1. 15 L’Esempio dell’Oro l Se F > Ser(T-t) – corto sul titolo privo di rischio di S (contanti) – corto sul forward che paga F per il titolo che oggi vale S – lungo sul titolo spot di S l fine periodo – pago Ser(T-t) a chi mi ha prestato i soldi – cedo il titolo alla somma F © 1999 di V. M. or J. H. 15

1. 16 L’Esempio dell’Oro l – – Per i beni d’investimento che non offrono «redditi» e non comportano «costi d’immagazzinamento» vale la relazione F Ser T t (3. 5) p. 51 © 1999 di V. M. or J. H. 16

1. 17 Petrolio: un’ Opportunità di Arbitraggio? l – – l Si supponga che: il prezzo spot del petrolio sia di $19 il prezzo forward a 1 anno del petrolio sia di $25 il «tasso d’interesse» a 1 anno in dollari sia del 5% annuo i costi di immagazzinamento del petrolio siano del 2% annuo C’è un’opportunità di arbitraggio? © 1999 di V. M. or J. H. 17

1. 18 Petrolio: un’Altra Opportunità di Arbitraggio? l – – l Si supponga che: il prezzo spot del petrolio sia di $19 il prezzo forward a 1 anno del petrolio sia di $16 il «tasso d’interesse» a 1 anno in dollari sia del 5% annuo i costi di immagazzinamento del petrolio siano del 2% annuo C’è un’opportunità di arbitraggio? © 1999 di V. M. or J. H. 18

1. 19 Obbligazione: un’Opportunità di Arbitraggio? l Si supponga che: – il prezzo spot di una obbligazione sia di € 50 – l’obbligazione paga interessi di € 0. 75 a 3, 6 e 9 mesi – il prezzo forward a 10 mesi è di € 53 – il tasso depo a 3, 6, 9 e 10 mesi è dell’ 8% l C’è un’opportunità di arbitraggio? © 1999 di V. M. or J. H. 19

1. 20 L’Esempio dell’Obbligazione l Se – corto sul titolo privo di rischio di S (contanti) – corto sul forward che paga F per il titolo che oggi vale S – lungo sul titolo spot di S l fine periodo – pago a chi mi ha prestato i soldi – cedo il titolo alla somma F – “guadagno” dai dividendi maturati © 1999 di V. M. or J. H. 20

1. 21 I Beni d’Investimento che Offrono Redditi Noti l Vale la relazione F S I er T t (3. 7) p. 52 dove I è il valore attuale dei redditi distribuiti (in quanto sono di diritto a coloro che prestano il titolo) © 1999 di V. M. or J. H. 21

1. 22 I Beni d’Investimento che Offrono un «Dividend Yield Noto» l Vale la relazione F Se r q T t (3. 10) p. 54 dove q è il dividend yield (dividendi in funzione del prezzo dell’azione) l Si assume che l’attività sottostante offra un reddito pari a q. S t nel periodo t © 1999 di V. M. or J. H. 22

1. 23 Forward con dividend yields • Supposto noto che chiamiamo dividend yield (annuo) • lo ‘spalmiamo’ sull’intero anno, cioè paga SqΔt per Δt 0, • in altre parole, dopo un giorno paga dividendi • dopo due giorni paga • in base a pag. 47 abbiamo che • ad es. S = 100, div(T)=110. 52 -100=10. 52= Seq. T - S • volendo attualizzare i dividendi: (Seq. T - S)e-q. T = S - e-q. T I • da cui: F=(S - I) er. T = (S - S + Se-q. T) er. T = Se(r-q)T © 1999 di V. M. or J. H. 23

1. 24 Valore di un Contratto Forward – Sia K: prezzo di consegna di un contratto forward F: prezzo forward che si applicherebbe ora al contratto – Il «valore» di un contratto forward lungo, f, è lungo f F K e r T t (3. 11) p. 55 – Analogamente, il «valore» di un contratto forward corto è f K F e r T t © 1999 di V. M. or J. H. 24

1. 25 Valore di un contratto Forward 0 l l t T Se F > K allora sono indifferente sse mi viene pagata una somma pari a F-K in T, ossia (F-K)e-r(-t) oggi, per vendere K. Dato che f(F)=0, si deduce che f(K)= (F-K)e-r(-t) Se F < K allora sono indifferente sse mi viene pagata una somma pari a K-F in T, ossia (K-F)e-r(-t) oggi, per acquistare K anziché F. Di conseguenza f(K)= -(K-F)e-r(-t) = (F-K)e-r(-t) © 1999 di V. M. or J. H. 25

1. 26 Valore di un contratto Forward l l l l 0 26/11 26/5 r = 6%, T - t = 6 mesi in T chi possiede K (è lungo di K) deve pagare $8. 32 meno di chi sottoscrive ora quindi. Quanto è la preferenza? 8. 32 e-6% / 2 = 8. 08 Chi vuole acquistare una posizione lunga su K pagherà 8. 08, (f = -8. 08) Chi vuole vendere una posizione lunga su K otterrà 8. 08, (f = 8. 08) Chi vuole acquistare una posizione corta su K pagherà 8. 08, (f = -8. 08) © 1999 di V. M. or J. H. 26

1. 27 Valore di un contratto Forward l Se f = $7 in che modo possiamo fare arbitraggio? l Volendo anticipare i guadagni? © 1999 di V. M. or J. H. 27

1. 28 Valore di un contratto Forward: senza redditi – Lunghi di forward F equivale al possesso di un sottostante S a scadenza T (qualunque sia il suo S valore in tale data): S t 0 0 t Deve valere come un portafoglio che T acquista oggi e dispone del titolo S in T © 1999 di V. M. or J. H. 28

1. 29 Valore di un contratto Forward: con redditi noti – Lunghi di forward F vuol dire acquistare il sottostante S in T (qualunque sia il suo valore in tale data), quindi senza i redditi maturati tra oggi e T: S 0 St 0 t Deve valere come un portafoglio T che dispone del titolo S in T © 1999 di V. M. or J. H. 29

1. 30 Valore di un contratto Forward: con dividend yields noti – Dato che gli interessi q. S t maturano “istantaneamente” (per piccoli t): S 0 St 0 t © 1999 di V. M. or J. H. T 30