1 1 1 Алгоритмы и структуры данных Жадные










![Activity-Selector(s,f) n=length[s] List A = <1> j=1 for i=2 to n do if s[i]>=f[j] Activity-Selector(s,f) n=length[s] List A = <1> j=1 for i=2 to n do if s[i]>=f[j]](https://present5.com/customparser/13669350_134947395 --- acd_10.ppt/slide_10.jpg)


![Дискретная задача о рюкзаке. Алгоритм. 1 for (i=0;i<=N ;i++) C[i] [0] = 0; 2 Дискретная задача о рюкзаке. Алгоритм. 1 for (i=0;i<=N ;i++) C[i] [0] = 0; 2](https://present5.com/customparser/13669350_134947395 --- acd_10.ppt/slide_15.jpg)










 1 1 1 Алгоритмы и структуры данных Жадные алгоритмы ЛЕКЦИЯ 10 Валенда Н.А. Кафедра Программной инженерии, факультет КН, ХНУРЕ
1 1 1 Алгоритмы и структуры данных Жадные алгоритмы ЛЕКЦИЯ 10 Валенда Н.А. Кафедра Программной инженерии, факультет КН, ХНУРЕ
 Методы программирования Жадные алгоритмы - производится локально оптимальный выбор в надежде, что он приведет к оптимальному решению всей задачи. Динамическое программирование – разбить задачу на подзадачи и не вычислять подзадачи более одного раза (использовать память).
Методы программирования Жадные алгоритмы - производится локально оптимальный выбор в надежде, что он приведет к оптимальному решению всей задачи. Динамическое программирование – разбить задачу на подзадачи и не вычислять подзадачи более одного раза (использовать память).
 Жадный алгоритм — алгоритм, заключается в принятии оптимальных решений на каждом шаге, где общее решение задачи складывается из оптимальных решений на предыдущих шагах. Для задач, решаемых жадными алгоритмами, характерны две особенности: к ним применим Принцип жадного выбора, они обладают свойством Оптимальности для подзадач.
Жадный алгоритм — алгоритм, заключается в принятии оптимальных решений на каждом шаге, где общее решение задачи складывается из оптимальных решений на предыдущих шагах. Для задач, решаемых жадными алгоритмами, характерны две особенности: к ним применим Принцип жадного выбора, они обладают свойством Оптимальности для подзадач.
 Принцип жадного выбора Говорят, что к оптимизационной задаче применим принцип жадного выбора, если последовательность локально оптимальных выборов даёт глобально оптимальное решение. В типичном случае доказательство оптимальности следует такой схеме: Доказывается, что жадный выбор на первом шаге не закрывает пути к оптимальному решению: для всякого решения есть другое, согласованное с жадным выбором и не хуже первого. Показывается, что подзадача, возникающая после жадного выбора на первом шаге, аналогична исходной. Рассуждение завершается по индукции. Оптимальность для подзадач Говорят, что задача обладает свойством оптимальности для подзадач, если оптимальное решение задачи содержит в себе оптимальные решения для всех её подзадач.
Принцип жадного выбора Говорят, что к оптимизационной задаче применим принцип жадного выбора, если последовательность локально оптимальных выборов даёт глобально оптимальное решение. В типичном случае доказательство оптимальности следует такой схеме: Доказывается, что жадный выбор на первом шаге не закрывает пути к оптимальному решению: для всякого решения есть другое, согласованное с жадным выбором и не хуже первого. Показывается, что подзадача, возникающая после жадного выбора на первом шаге, аналогична исходной. Рассуждение завершается по индукции. Оптимальность для подзадач Говорят, что задача обладает свойством оптимальности для подзадач, если оптимальное решение задачи содержит в себе оптимальные решения для всех её подзадач.
 Дано: множество процессов S = {a1, а2,..., an}, процессам требуется некоторый ресурс, который одновременно может использоваться лишь одним процессом. Каждый процесс ai характеризуется начальным моментом si и конечным моментом fi, где 0 ≤ si < fi < ∞. Будучи выбран, процесс ai длится в течение [si, fi) (конец одного процесса может совпадать с началом другого процесса, это не считается пересечением ), процессы ai и aj совместимы, если интервалы [si,fi) и[sj, fj) не перекрываются. Найти: подмножество взаимно совместимых процессов, образующих множество максимального размера. Задача о выборе процессов
Дано: множество процессов S = {a1, а2,..., an}, процессам требуется некоторый ресурс, который одновременно может использоваться лишь одним процессом. Каждый процесс ai характеризуется начальным моментом si и конечным моментом fi, где 0 ≤ si < fi < ∞. Будучи выбран, процесс ai длится в течение [si, fi) (конец одного процесса может совпадать с началом другого процесса, это не считается пересечением ), процессы ai и aj совместимы, если интервалы [si,fi) и[sj, fj) не перекрываются. Найти: подмножество взаимно совместимых процессов, образующих множество максимального размера. Задача о выборе процессов
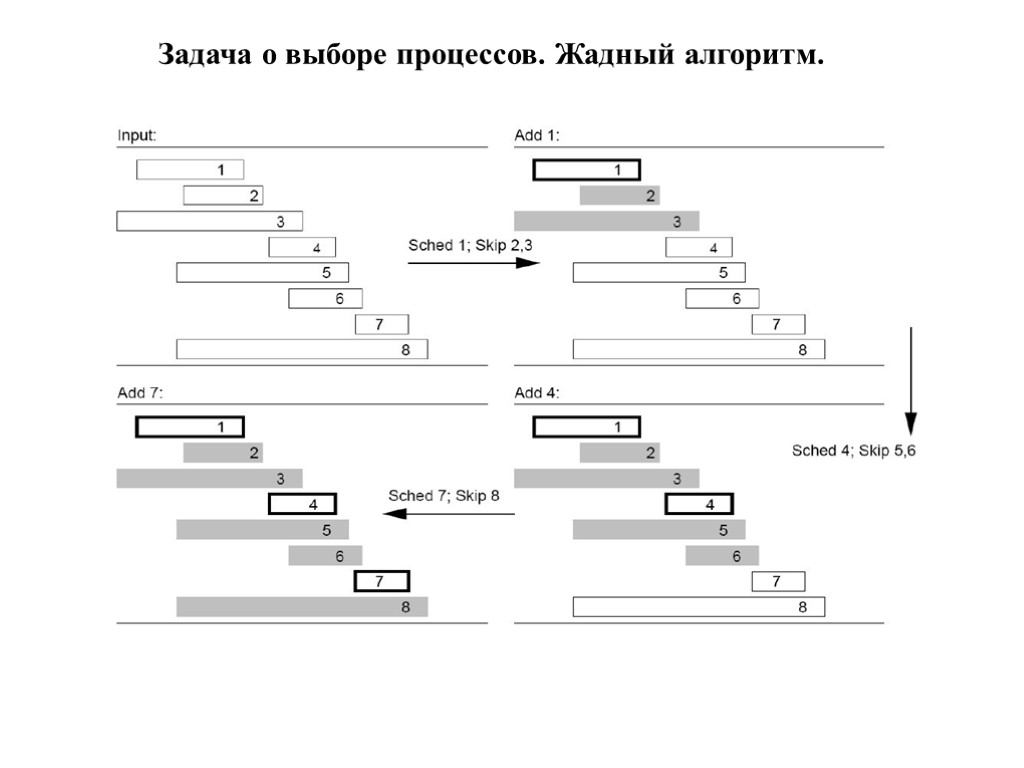
 Пусть S отсортировано по f в порядке возрастания за время O(n log n). В результирующее множество процессов заносим 1 процесс (поскольку он заканчивается раньше всех остальных) Из множества процессов убираем те, которые конфликтуют с выбранным процессом Повторяем алгоритм для меньшего количества процессов Сложность алгоритма O(n log n+ n). Задача о выборе процессов. Оптимальное решение. Жадный алгоритм
Пусть S отсортировано по f в порядке возрастания за время O(n log n). В результирующее множество процессов заносим 1 процесс (поскольку он заканчивается раньше всех остальных) Из множества процессов убираем те, которые конфликтуют с выбранным процессом Повторяем алгоритм для меньшего количества процессов Сложность алгоритма O(n log n+ n). Задача о выборе процессов. Оптимальное решение. Жадный алгоритм
 В доказательстве исследуется глобальное оптимальное решение некоторой подзадачи. Затем демонстрируется, что решение можно преобразовать так, чтобы в нем использовался жадный выбор, в результате чего получится аналогичная, но более простая подзадача. Все процессы отсортированы по неубыванию времени окончания. Процесс номер 1, очевидно, входит в оптимум (если нет, то заменим самый ранний процесс в оптимуме на него, что не повредит совместимости процессов). Убрав все процессы, противоречащие первому, получим исходную задачу с меньшим количеством процессов. Рассуждая по индукции, получаем, что делая на каждом шаге жадный выбор, приходим к оптимальному решению. Задача о выборе процессов. Оптимальное решение. Жадный алгоритм
В доказательстве исследуется глобальное оптимальное решение некоторой подзадачи. Затем демонстрируется, что решение можно преобразовать так, чтобы в нем использовался жадный выбор, в результате чего получится аналогичная, но более простая подзадача. Все процессы отсортированы по неубыванию времени окончания. Процесс номер 1, очевидно, входит в оптимум (если нет, то заменим самый ранний процесс в оптимуме на него, что не повредит совместимости процессов). Убрав все процессы, противоречащие первому, получим исходную задачу с меньшим количеством процессов. Рассуждая по индукции, получаем, что делая на каждом шаге жадный выбор, приходим к оптимальному решению. Задача о выборе процессов. Оптимальное решение. Жадный алгоритм
 Aij = {sk S : fi ≤ sk < fk ≤ sj} - подмножество процессов, которые можно выполнить в промежутке между завершением ai и началом aj Оптимальное решение задачи Sj равно Aij = Aik ak Akj Оптимальное решение всей задачи представляет собой решение задачи S0,n+1. c [i, j] — количество процессов в подмножестве максимального размера, состоящем из взаимно совместимых процессов в задаче Sij. Если процесс ak используется в максимальном подмножестве, состоящем из взаимно совместимых процессов задачи Sij , то для подзадач Sik и Skj также используются подмножества максимального размера. Получаем рекуррентное соотношение Задача о выборе процессов. Оптимальное решение. Динамическое программирование
Aij = {sk S : fi ≤ sk < fk ≤ sj} - подмножество процессов, которые можно выполнить в промежутке между завершением ai и началом aj Оптимальное решение задачи Sj равно Aij = Aik ak Akj Оптимальное решение всей задачи представляет собой решение задачи S0,n+1. c [i, j] — количество процессов в подмножестве максимального размера, состоящем из взаимно совместимых процессов в задаче Sij. Если процесс ak используется в максимальном подмножестве, состоящем из взаимно совместимых процессов задачи Sij , то для подзадач Sik и Skj также используются подмножества максимального размера. Получаем рекуррентное соотношение Задача о выборе процессов. Оптимальное решение. Динамическое программирование
 Возможные значения для k : i +1,...,j − 1. Поскольку в подмножестве максимального размера для задачи Sij должно использоваться одно из этих значений k, нужно проверить, какое из них подходит лучше других. Таким образом, полное рекурсивное определение величины c [i, j] принимает вид: Задача о выборе процессов. Оптимальное решение. Динамическое программирование
Возможные значения для k : i +1,...,j − 1. Поскольку в подмножестве максимального размера для задачи Sij должно использоваться одно из этих значений k, нужно проверить, какое из них подходит лучше других. Таким образом, полное рекурсивное определение величины c [i, j] принимает вид: Задача о выборе процессов. Оптимальное решение. Динамическое программирование
![>Activity-Selector(s,f) n=length[s] List A = <1> j=1 for i=2 to n do if s[i]>=f[j] >Activity-Selector(s,f) n=length[s] List A = <1> j=1 for i=2 to n do if s[i]>=f[j]](https://present5.com/customparser/13669350_134947395 --- acd_10.ppt/slide_10.jpg) Activity-Selector(s,f) n=length[s] List A = <1> j=1 for i=2 to n do if s[i]>=f[j] then append i to A j=i return A Задача о выборе процессов. Жадный алгоритм
Activity-Selector(s,f) n=length[s] List A = <1> j=1 for i=2 to n do if s[i]>=f[j] then append i to A j=i return A Задача о выборе процессов. Жадный алгоритм
 Задача о выборе процессов. Жадный алгоритм.
Задача о выборе процессов. Жадный алгоритм.
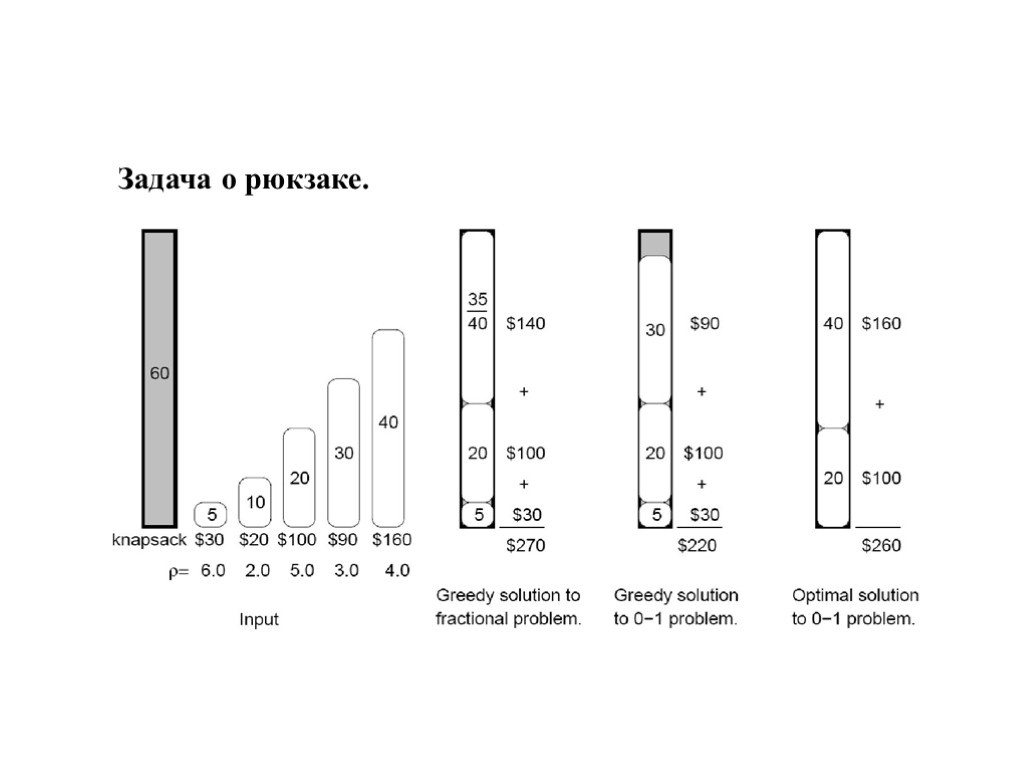
 Дискретная задача о рюкзаке Дано: N предметов {x1, x2,..., xN} с различной стоимостью Vi и весом Wi максимальный вес Wmax. Найти: подмножество предметов, вес которых бы не превышал Wmax, стоимость которых, была бы максимальной. Непрерывная задача о рюкзаке теперь тот или иной товар можно брать с собой частично, а не целиком. В дискретной задаче о рюкзаке в роли предметов могут выступать, например, слитки золота, а для непрерывной задачи больше подходят такие товары, как золотой песок.
Дискретная задача о рюкзаке Дано: N предметов {x1, x2,..., xN} с различной стоимостью Vi и весом Wi максимальный вес Wmax. Найти: подмножество предметов, вес которых бы не превышал Wmax, стоимость которых, была бы максимальной. Непрерывная задача о рюкзаке теперь тот или иной товар можно брать с собой частично, а не целиком. В дискретной задаче о рюкзаке в роли предметов могут выступать, например, слитки золота, а для непрерывной задачи больше подходят такие товары, как золотой песок.
 Задача о рюкзаке.
Задача о рюкзаке.
 Дискретная задача о рюкзаке. Описание структуры Ciw - максимальная стоимость предметов из множества {x1, х2,..., xi} при максимальном весе равном w. Ответ: CNW
Дискретная задача о рюкзаке. Описание структуры Ciw - максимальная стоимость предметов из множества {x1, х2,..., xi} при максимальном весе равном w. Ответ: CNW
![>Дискретная задача о рюкзаке. Алгоритм. 1 for (i=0;i<=N ;i++) C[i] [0] = 0; 2 >Дискретная задача о рюкзаке. Алгоритм. 1 for (i=0;i<=N ;i++) C[i] [0] = 0; 2](https://present5.com/customparser/13669350_134947395 --- acd_10.ppt/slide_15.jpg) Дискретная задача о рюкзаке. Алгоритм. 1 for (i=0;i<=N ;i++) C[i] [0] = 0; 2 for (w=0;w<=Wmax;w++) C[0] [w] = 0; 3 4 for (i=l;i<=N;i++) 5 for (w=l;w<=Wmax;w++) { 6 if (Wi[i] > w) 7 C[i] [w] = C[i-1] [w] ; 8 else 9 C[i][w] = max(C[i-l] [w] , С [i-1] [w-Wi [i] ] +Vi [i] ); 10 } 11 12 output(С[N][Wmax]);
Дискретная задача о рюкзаке. Алгоритм. 1 for (i=0;i<=N ;i++) C[i] [0] = 0; 2 for (w=0;w<=Wmax;w++) C[0] [w] = 0; 3 4 for (i=l;i<=N;i++) 5 for (w=l;w<=Wmax;w++) { 6 if (Wi[i] > w) 7 C[i] [w] = C[i-1] [w] ; 8 else 9 C[i][w] = max(C[i-l] [w] , С [i-1] [w-Wi [i] ] +Vi [i] ); 10 } 11 12 output(С[N][Wmax]);
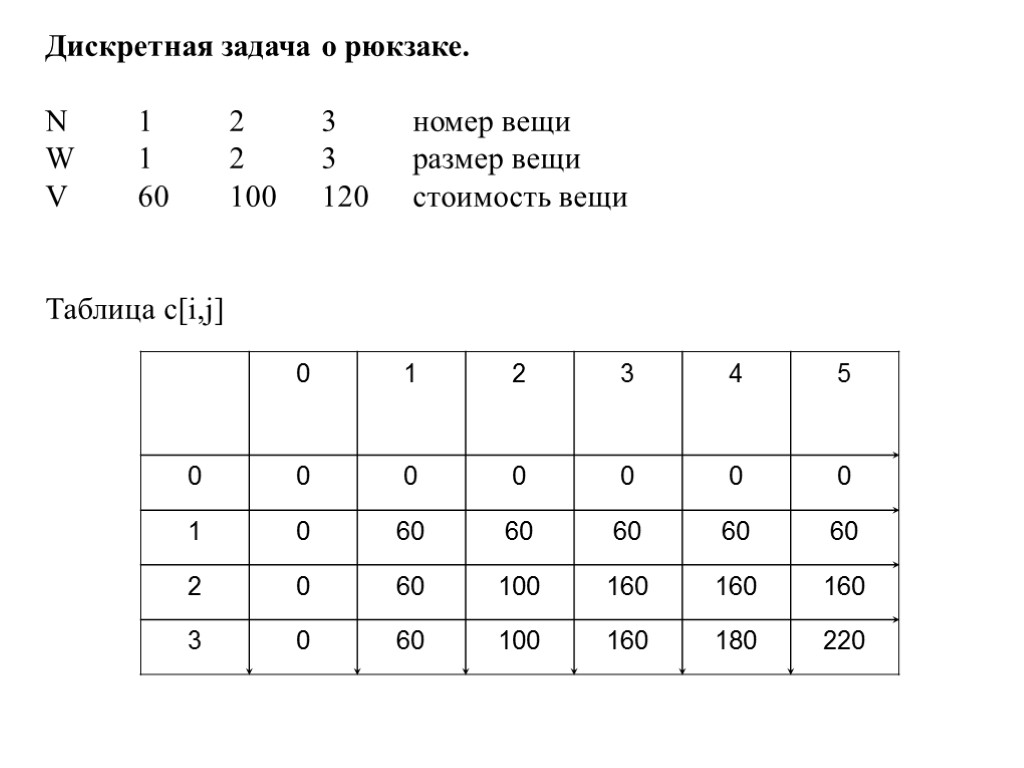
 Дискретная задача о рюкзаке. N 1 2 3 номер вещи W 1 2 3 размер вещи V 60 100 120 стоимость вещи Таблица с[i,j]
Дискретная задача о рюкзаке. N 1 2 3 номер вещи W 1 2 3 размер вещи V 60 100 120 стоимость вещи Таблица с[i,j]
 Дискретная задача о рюкзаке. Анализ алгоритма. T(N) = (N * Wmax)
Дискретная задача о рюкзаке. Анализ алгоритма. T(N) = (N * Wmax)
 Непрерывная задача о рюкзаке Отсортировать веши в порядке убывания цены на единицу веса Самую ценную вещь поместить в рюкзак целиком или частично, если остаток рюкзака меньше вещи Изъять вещь из рассматриваемого множества Если рюкзак не полон перейти к шагу 2.
Непрерывная задача о рюкзаке Отсортировать веши в порядке убывания цены на единицу веса Самую ценную вещь поместить в рюкзак целиком или частично, если остаток рюкзака меньше вещи Изъять вещь из рассматриваемого множества Если рюкзак не полон перейти к шагу 2.
 Коды Хаффмена Любое сообщение состоит из последовательности символов некоторого алфавита. Зачастую для экономии памяти, для увеличения скорости передачи информации возникает задача сжатия информации . В этом случае используются специальные методы кодирования символов. К таким относятся коды Хаффмена, которые дают сжатие от 20% до 90% в зависимости от типа информации. Алгоритм Хаффмена находит оптимальные коды символов исходя из частоты использования символов в сжимаемом тексте. Алгоритм Хаффмена является примером жадного алгоритма .
Коды Хаффмена Любое сообщение состоит из последовательности символов некоторого алфавита. Зачастую для экономии памяти, для увеличения скорости передачи информации возникает задача сжатия информации . В этом случае используются специальные методы кодирования символов. К таким относятся коды Хаффмена, которые дают сжатие от 20% до 90% в зависимости от типа информации. Алгоритм Хаффмена находит оптимальные коды символов исходя из частоты использования символов в сжимаемом тексте. Алгоритм Хаффмена является примером жадного алгоритма .
 Пусть в файле длины 100000 символы известны частоты символов: Коды Хаффмена
Пусть в файле длины 100000 символы известны частоты символов: Коды Хаффмена
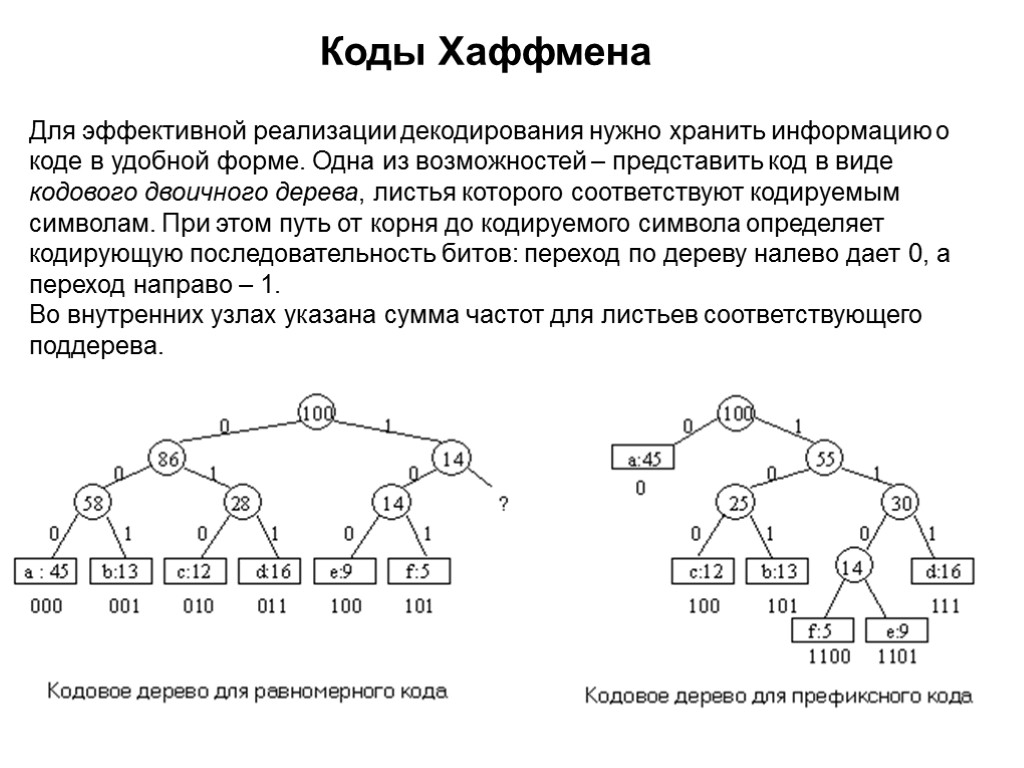
 Коды Хаффмена Нужно построить двоичный код, в котором каждый символ представляется в виде конечной последовательности битов, называемой кодовым словом. При использовании равномерного кода, в котором все кодовые слова имеют одинаковую длину, на каждый символ тратится минимум три бита и на весь файл уйдет 300000 битов. Неравномерный код будет экономнее, если часто встречающиеся символы закодировать короткими последовательностями битов, а редко встречающиеся символы – длинными. При кодировке на весь файл уйдет (45*1 + 13*3 + 12*3 + 16*3 + 9*4 + 5*4)*1000 = 224000. То есть, неравномерный код дает около 25% экономии.
Коды Хаффмена Нужно построить двоичный код, в котором каждый символ представляется в виде конечной последовательности битов, называемой кодовым словом. При использовании равномерного кода, в котором все кодовые слова имеют одинаковую длину, на каждый символ тратится минимум три бита и на весь файл уйдет 300000 битов. Неравномерный код будет экономнее, если часто встречающиеся символы закодировать короткими последовательностями битов, а редко встречающиеся символы – длинными. При кодировке на весь файл уйдет (45*1 + 13*3 + 12*3 + 16*3 + 9*4 + 5*4)*1000 = 224000. То есть, неравномерный код дает около 25% экономии.
 Префиксные коды Рассмотрим коды, в которых для каждой из двух последовательностей битов, представляющих различные символы, ни одна не является префиксом другой. Такие коды называются префиксными кодами. При кодировании каждый символ заменяется на свой код. Например, строка abc выглядит как 0101100. Для префиксного кода декодирование однозначно и выполняется слева направо. Первый символ текста, закодированного префиксным кодом, определяется однозначно, так как его кодовое слово не может быть началом какого-либо другого символа. Определив этот символ и отбросив его кодовое слово, повторяем процесс для оставшихся битов и так далее. Например, строка 001011101 разбивается на части 0.0.101.1101 и декодируется как aabe. Коды Хаффмена
Префиксные коды Рассмотрим коды, в которых для каждой из двух последовательностей битов, представляющих различные символы, ни одна не является префиксом другой. Такие коды называются префиксными кодами. При кодировании каждый символ заменяется на свой код. Например, строка abc выглядит как 0101100. Для префиксного кода декодирование однозначно и выполняется слева направо. Первый символ текста, закодированного префиксным кодом, определяется однозначно, так как его кодовое слово не может быть началом какого-либо другого символа. Определив этот символ и отбросив его кодовое слово, повторяем процесс для оставшихся битов и так далее. Например, строка 001011101 разбивается на части 0.0.101.1101 и декодируется как aabe. Коды Хаффмена
 Для эффективной реализации декодирования нужно хранить информацию о коде в удобной форме. Одна из возможностей – представить код в виде кодового двоичного дерева, листья которого соответствуют кодируемым символам. При этом путь от корня до кодируемого символа определяет кодирующую последовательность битов: переход по дереву налево дает 0, а переход направо – 1. Во внутренних узлах указана сумма частот для листьев соответствующего поддерева. Коды Хаффмена
Для эффективной реализации декодирования нужно хранить информацию о коде в удобной форме. Одна из возможностей – представить код в виде кодового двоичного дерева, листья которого соответствуют кодируемым символам. При этом путь от корня до кодируемого символа определяет кодирующую последовательность битов: переход по дереву налево дает 0, а переход направо – 1. Во внутренних узлах указана сумма частот для листьев соответствующего поддерева. Коды Хаффмена
 Оптимальному для данного файла коду всегда соответствует двоичное дерево, в котором всякая вершина , не являющаяся листом, имеет двух сыновей. Равномерный код не является оптимальным, так как в соответствующем ему дереве есть вершина с одним сыном. Дерево оптимального префиксного кода для файла, в котором используются все символы из некоторого множества С и только они содержат ровно | С | листьев по одному на каждый символ и ровно | С | - 1 узлов , не являющихся листьями. Зная дерево Т, соответствующее префиксному коду, легко найти количество битов, необходимое для кодирования файла. Для каждого символа с из алфавита С, пусть f [c] означает число его вхождений в файл, а dT (c) – глубину соответствующего ему листа и, следовательно, длину последовательности битов, кодирующей с. Тогда для кодирования файла потребуется: битов Эта величина называется стоимостью дерева Т. Необходимо минимизировать эту величину. Коды Хаффмена
Оптимальному для данного файла коду всегда соответствует двоичное дерево, в котором всякая вершина , не являющаяся листом, имеет двух сыновей. Равномерный код не является оптимальным, так как в соответствующем ему дереве есть вершина с одним сыном. Дерево оптимального префиксного кода для файла, в котором используются все символы из некоторого множества С и только они содержат ровно | С | листьев по одному на каждый символ и ровно | С | - 1 узлов , не являющихся листьями. Зная дерево Т, соответствующее префиксному коду, легко найти количество битов, необходимое для кодирования файла. Для каждого символа с из алфавита С, пусть f [c] означает число его вхождений в файл, а dT (c) – глубину соответствующего ему листа и, следовательно, длину последовательности битов, кодирующей с. Тогда для кодирования файла потребуется: битов Эта величина называется стоимостью дерева Т. Необходимо минимизировать эту величину. Коды Хаффмена
 Хаффмен предложил жадный алгоритм, который строит оптимальный префиксный код. Алгоритм строит дерево Т, соответствующее оптимальному коду снизу вверх, начиная с множества из | С | листьев и делая | С | - 1 слияний. Для каждого символа задана его частота f [c]. Для нахождения двух объектов для слияния используется очередь с приоритетами Q, использующая частоты f в качестве приоритетов – сливаются два объекта с наименьшими частотами. В результате слияния получается новый объект (внутренняя вершина), частота которого считается равной сумме частот двух сливаемых объектов. Эта вершина заносится в очередь. Коды Хаффмена
Хаффмен предложил жадный алгоритм, который строит оптимальный префиксный код. Алгоритм строит дерево Т, соответствующее оптимальному коду снизу вверх, начиная с множества из | С | листьев и делая | С | - 1 слияний. Для каждого символа задана его частота f [c]. Для нахождения двух объектов для слияния используется очередь с приоритетами Q, использующая частоты f в качестве приоритетов – сливаются два объекта с наименьшими частотами. В результате слияния получается новый объект (внутренняя вершина), частота которого считается равной сумме частот двух сливаемых объектов. Эта вершина заносится в очередь. Коды Хаффмена
 Huffman (C) 1. n ←│C│ │C│- мощность С 2. Q ← C Q – очередь с приоритетами 3. for i ← 1 to n-1 4. do z ← Create_Node ( ) z – узел, состоящий из полей f, left, right 5. x ← left [z] ← Dequeue (Q) 6. y ← right [z] ← Dequeue (Q) 7. f[z] ← f[x] + f[y] 8. Enqueue (Q, z) 9. return Dequeue (Q) вернуть корень дерева Коды Хаффмена
Huffman (C) 1. n ←│C│ │C│- мощность С 2. Q ← C Q – очередь с приоритетами 3. for i ← 1 to n-1 4. do z ← Create_Node ( ) z – узел, состоящий из полей f, left, right 5. x ← left [z] ← Dequeue (Q) 6. y ← right [z] ← Dequeue (Q) 7. f[z] ← f[x] + f[y] 8. Enqueue (Q, z) 9. return Dequeue (Q) вернуть корень дерева Коды Хаффмена
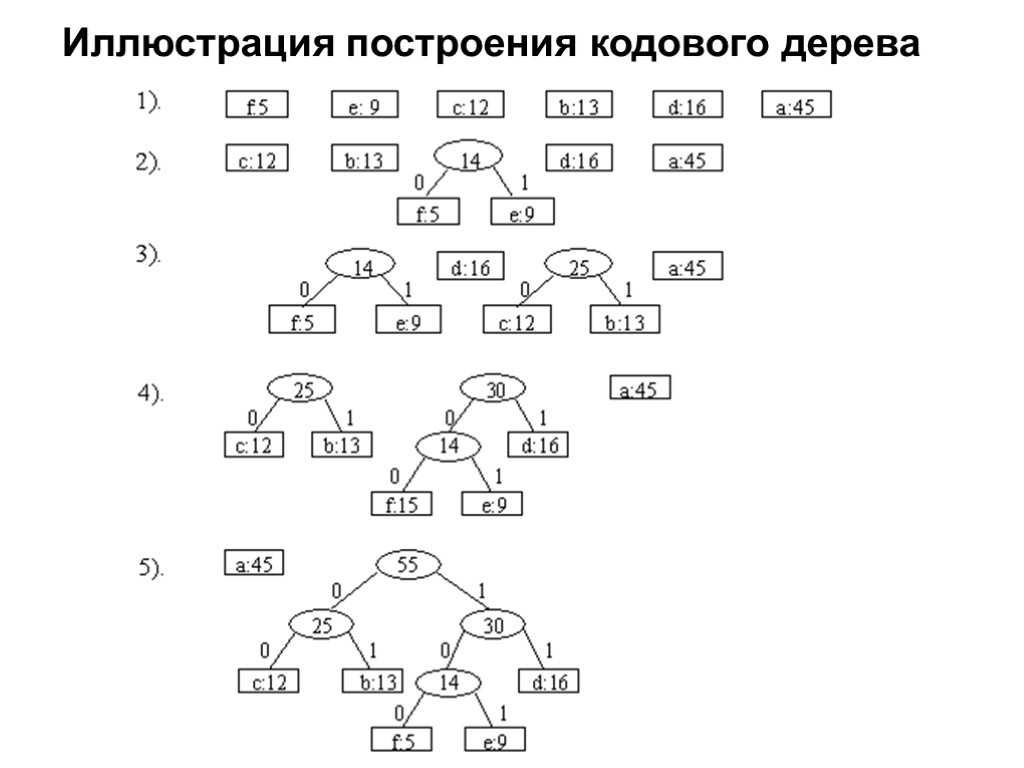
 Иллюстрация построения кодового дерева
Иллюстрация построения кодового дерева
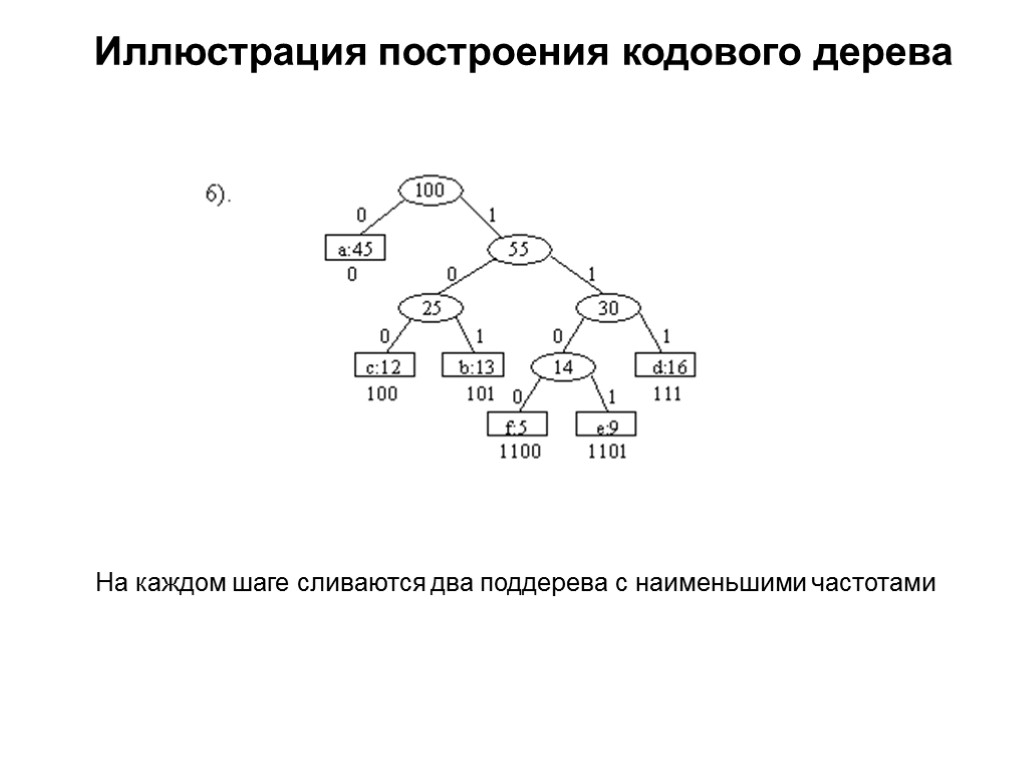
 Иллюстрация построения кодового дерева На каждом шаге сливаются два поддерева с наименьшими частотами
Иллюстрация построения кодового дерева На каждом шаге сливаются два поддерева с наименьшими частотами
 Оценка алгоритма Очередь реализована в виде двоичной кучи. Создать очередь можно за O(n). Алгоритм состоит из цикла, который выполняется n-1 раз. Каждая операция с очередью выполняется за O(log n). Общее время работы O(n log n).
Оценка алгоритма Очередь реализована в виде двоичной кучи. Создать очередь можно за O(n). Алгоритм состоит из цикла, который выполняется n-1 раз. Каждая операция с очередью выполняется за O(log n). Общее время работы O(n log n).

