


1. 如图 ,一只转 盘 均 匀 分 成 8部 分 , 每 一 部 分 标 有 1~ 8个 数. 现 转 动 转 盘,则转盘停止转动时, D 指针 指向偶数的概率是( ) B. A. C. D.

根据标 有偶数与奇数所占面 积 相等, 由几何概型公式易得指针 指 向偶数的概率是 , 选 D.
2. 在 2升的水中有一个草履虫,现 从中随 机取出 0. 3升水样 放到显 微镜 下观 察,则 发 B 现草履虫的概率是( ) A. B. C. D. 由于取水样 的随机性,所求事件“ 在取出 0. 3升的水样 中有草履虫”的概率等于 水样的体积与总体积之比

3. 某公共汽车站每隔 5分钟有一辆汽车到达, 乘客到达汽车站的时刻是任意的,则一个乘客 候车时间不超过3分钟的概率是( )C A. B. C. D. 因为离上一次公共汽车通过后的2分 钟到 5分钟的任一时刻乘客到站,候车都不超 过3分钟,所以P(A)= ,故选C.
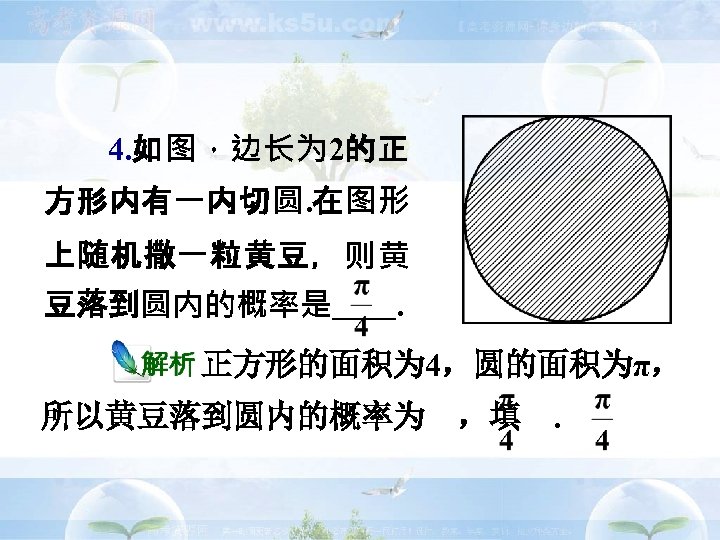
4. 如图,边长为 2的正 方形内有一内切圆. 在图形 上随机撒一粒黄豆,则黄 豆落到圆内的概率是 . 正方形的面积为 4,圆的面积为π, 所以黄豆落到圆内的概率为 ,填 .

5. 设P为圆周上一定点,在圆周上等可 能地任取一点与P连接,则弦长超过半径的 概率为 . 当弦长等于半径时,对应的圆心 角为 ,设事件A为“弦长超过半径”, 则 填 . 易错点:事件区域的确定. 本题是与 角度有关的几何概型.

1. 几何概型 如果每个事件发 生的概率只与构成该 事 件区域的长 度(面积 或体积 )成比例,则 称这 样的概率模型为几何概率模型. 几何概型有如下特点 (1)试 验 中所有可能出现 的结 果(基本事件 )有无限多个; (2)每个基本事件出现的可能性相等.

2. 几何概型的概率公式: 构成事件A的区域长度(面积或体积) 试验的全部结果所构成的区域长度(面积或体积) P(A)= 3. 随机数就是在一定的范围 内随机产 生的 数,并且得到这 个范围 内的每一个数的机会 一样.

重点突破:与长度有关的几何概型 在长为 10 cm的线段AB上取一点G, 并以AG为半径作一个圆,则圆的面积介于 36π cm 2到 64π cm 2的概率为 . 点G随机地落在线段AB上,故试 验所有点所在的区域为线段AB. 圆的面积介于 36π cm 2到 64π cm 2,即圆的半径介于6 cm到 8 cm之间,与A相距 6 cm到 8 cm的区域即为构成 圆的面积介于36π cm 2到 64π cm 2的事件.

因为事件满足几何概型,事件发 生的总区域为线段AB,其长度为 10 cm. 设“圆的面积介于36 cm 2到 64 cm 2”为事件 B,当点G与A相距 6 cm到 8 cm时,以AG为半 径的圆,其面积介于36π cm 2到 64π cm 2,故满 足“圆的面积介于36π cm 2到 64π cm 2”的点所在 的区域的线段长度为 2 cm. 所以

我们将每一个基本事件理解为从某 个特定的几何区域内随机地取一点,该区域中 每一点被取到的机会都一样,而一个随机事件 的发生则理解为恰好取到上述区域内的某个指 定区域中的点,这样的概率模型就可以用几何 概型来求解. 解答本类问题的关键是将基本事 件的全部及其事件A包含的基本事件转化为相 应线段的长度,进而求解.

如图,A、B两盏路灯之间长 度是 30米,由于光线较暗,想在其间再随意 安装两盏路灯C、D,问A与C,B与D之间的 距离都不小于10米的概率是多少? 记事件E为:“A与C,B与D之间 的距离都不小于10米”,把AB三等分,事件E 构成的区域为中间这一部分,由于中间长度 为 30× =10米,所以

重点突破:与面积(体积)有关的几何 概型 一只蚂蚁在边长分别为 6, 8, 10的三角 形区域内随机爬行,则其恰在离三个顶点距 D 离都大于2的地方的概率为( ) A. B. C. D.

事件发生的区域为△ABC平 面区域,“恰在离三个顶点距离都大于2” 的区域为图中阴影部分区域,属于几何概 型中的面积比问题.
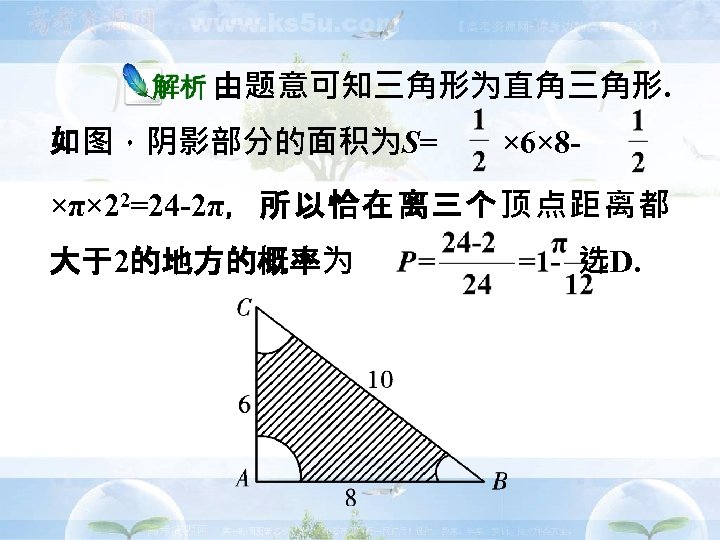
由题意可知三角形为直角三角形. 如图,阴影部分的面积为S= × 6× 8 - ×π× 22=24 -2π,所以恰在离三个顶点距离都 大于2的地方的概率为 选D.

直接求阴影部分的面积比较困难, 因此转化为求三部分扇形面积,体现“正难则 反”的化归与转化思想;紧接着,求三部分扇 形面积时,考虑扇形的半径均为 2,且所对应 的圆心角的和为π,刚好可组成半圆,基于此, 利用“补形”思想方法,这都是解题常用的策略, 需要加强训练.

在平面直角坐标系中有四个点; A(0, 0)、B(2, 0)、C(1, )、D(3, 2), 若 向 △ABD内 随 机 投 掷 一 质 点 , 则 它 落 在 C △ACB内的概率为( ) A. B. C. D.

在平面直角坐标系作出点的坐标, 可以发现△ACB区域在△ABD区域的内部, 所以质点落在△ACB内的概率为 选C. ,
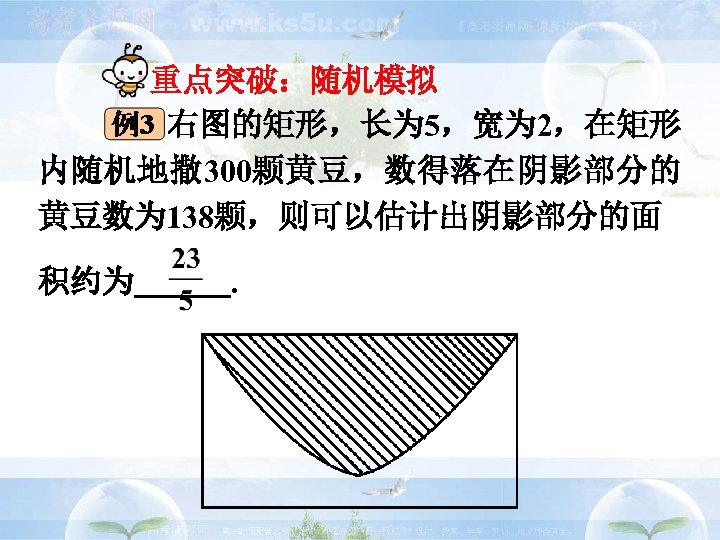
重点突破:随机模拟 右图的矩形,长为 5,宽为 2,在矩形 内随机地撒 300颗黄豆,数得落在阴影部分的 黄豆数为 138颗,则可以估计出阴影部分的面 积约为 .

随机撒一把黄豆,每个黄豆落 在矩形内任何一点是等可能的,落在每个区 域的黄豆数与这个区域的面积近似成正比, 阴暗部分的面积 落在阴暗部分的黄豆数 , 即 ≈ 矩形的面积 落在矩形的黄豆数 从此入手,即可估计出阴影部分的面积.

矩形面积为 5× 2=10,故阴影部分的 面积约为 本例启发我们,利用几何概型,并 通过随机模拟方法可以近似估算不规则图形的 面积,这就是数学的价值.

y≥ 0 x+y-2≤ 0 的点(x, y) 设满足 x-y+2≥ 0 构成的区域为D,又知区域D内的每一个点都在 区域M内. 为了测算区域M的面积,向区域M内 随机抛入 10000个质点,经统计,落在区域D内 的质点有2500个,则区域M的面积大约是 16.

y≥ 0 满足 x+y-2≤ 0 的点(x, y)构成的区 x-y+2≥ 0 域为三角形,其面积为 × 4× 2=4, 故区域M的面积大约为 填 16.

已知三个正数a, b, c满足a<b<c. (Ⅰ)若a, b, c是从 中任取的三 个数,求a, b, c能构成三角形三边长的概率; (Ⅱ)若a, b, c是从(0, 1)中任取的三个数,求 a, b, c能构成三角形三边长的概率.
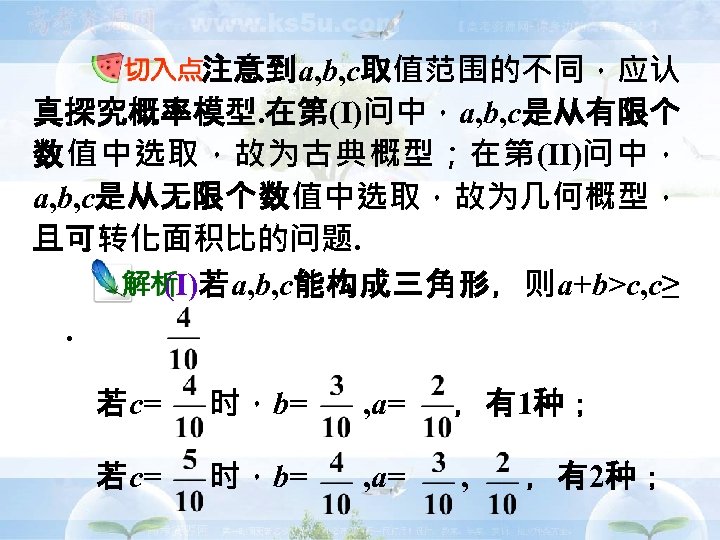
注意到a, b, c取值范围的不同,应认 真探究概率模型. 在第(Ⅰ)问中,a, b, c是从有限个 数值中选取,故为古典概型;在第(Ⅱ)问中, a, b, c是从无限个数值中选取,故为几何概型, 且可转化面积比的问题. (Ⅰ)若a, b, c能构成三角形,则a+b>c, c≥ . 若c= 时,b= , a= ,有1种; 时,b= , a= , 若c= ,有2种;

同理c= 时,有3+1=4种;c= 时,有 4+2=6种; c= 时 , 有 5+3+1=9种 ; c= 时,有 6+4+2=12种. 于是共有1+2+4+6+9+12=34种. 从 中任取的三个数a, b, c( a<b<c)的方法数有84种, 所以a, b, c能构成三角形的概率

(Ⅱ)a、b、c能构成三角形的充要条件是 0<a<b<c<1, a+b>c, 0<c<1. 在坐标系a. Ob内画出 满足以上条件的区域(如图 阴影部分),由几何概型的 计算方法可知,求阴影部分的面积与图中正方 形的面积比即可. 又S阴影= ,于是所要求的概率

本题涉及几何概型和古典概型, 题目简捷明了,有助于认识几何概型和古典 概型的区别与联系;其次,在解决几何概型 问题时,应先根据题意确定是与长度、角度、 面积还是体积有关的模型,然后求出事件A和 基本事件的几何度量,借助几何概型的计算 公式求解.

1. 几何概型与古典概型的异同点 几何概型是与古典概型最为接近的一种概 率模型. 两者的共同点是基本事件是等可能的, 不同点是基本事件数一个是有限的,一个是无 限的. 基本事件可以抽象为点,对于几何概型, 这些点尽管是无限的,但它们所占据的区域是 有限的,根据等可能性,这个点落在区域的概 率与该区域的几何度量成正比,而与该区域的 位置和形状无关.

2. 几何概型概率的适用条件 使用几何概型的概率计算公式时,一定要 注意其适用条件:每个事件发生的概率只与构 成该事件区域的长度(面积或体积)成比例. 同时要注意判断基本事件的等可能性,这需要 严谨思维,切忌想当然,需要从问题的实际背 景中去判断.

1. (2009·福建卷)点A为周长等于3的圆 周上的一个定点,若在该圆周上随机取一点B, 则劣弧AB的长度小于1的概率为 . 圆周上使弧 的长度为 1的点M有 两个,设为M 1、M 2,则过A的圆弧 长度 为 2,B点落在优弧 长度小于1,所以劣弧 为 ,填 . 上就能使劣弧 的 的长度小于1的概率

几何概型是高中新课程新增的内容, 考查形式多样灵活,可以与现实生活和实际应 用问题广泛结合. 利用几何概型方法将概率问 题转化为长度比、面积比、体积比问题是解决 该类问题的常用手段,简单线性规划、解三角 形及定积分是解决该类问题的主要 具.

2. ( 2009·辽 宁 卷 ) ABCD为 长 方 形 , AB=2, BC=1, O为 AB的 中 点 , 在 长 方 形 ABCD内随机取一点,取到的点到O的距离大 B 于1的概率为( ) A. B. 1 - C. D. 1 -
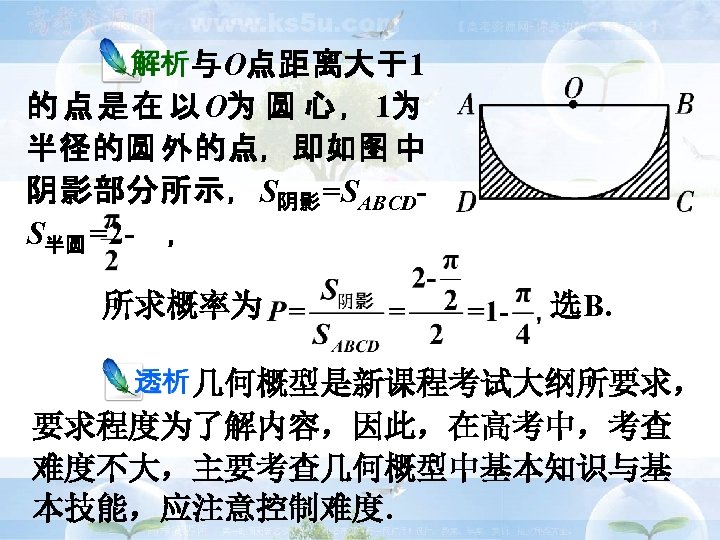
与O点距离大于1 的 点 是 在 以 O为 圆 心 , 1为 半径的圆 外的点,即如图 中 阴影部分所示,S阴影 =SABCDS半圆 =2 - , 所求概率为 选B. 几何概型是新课程考试大纲所要求, 要求程度为了解内容,因此,在高考中,考查 难度不大,主要考查几何概型中基本知识与基 本技能,应注意控制难度.