2. Алгебра высказываний.pptx
- Количество слайдов: 27

08. 02. 2018 Математическая логика. Алгебра высказываний.

Основная задача логики заключается в том, чтобы на основании истинности или ложности простых высказываний определить истинность или ложность сложных высказываний.

Алгебра высказываний Алгебра логики отвлекается от смысловой содержательности высказываний. Ее интересует только один факт истинно или ложно данное высказывание, что дает возможность определять истинность или ложность составных высказываний алгебраическими методами.

Алгебра высказываний Простые высказывания в алгебре логики обозначаются заглавными латинскими буквами: А = {Аристотель - основоположник логики} В = {На яблонях растут бананы}. Истинному высказыванию ставится в соответствие 1, ложному — 0. Таким образом, А = 1, В = 0.

Алгебра высказываний Составные высказывания на естественном языке образуются с помощью союзов, которые в алгебре высказываний заменяются на логические операции. Логическая операция – способ построения сложного высказывания из данных высказываний, при котором значение истинности сложного высказывания полностью определяется значениями истинности исходных высказываний.

1. Конъюнкция (логическое умножение): Например: На автостоянке стоят «Мерседес» и «Жигули» . Союз и; Обозначение A&B, A B, A*B, A И B В языках программирования обозначение And.
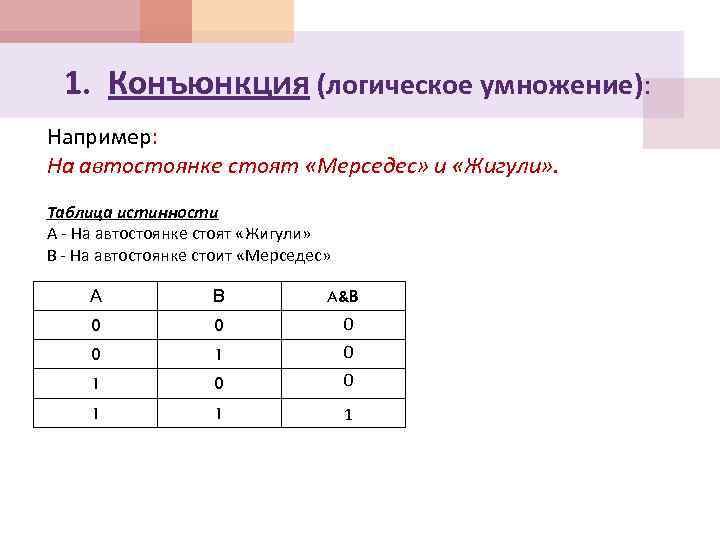
1. Конъюнкция (логическое умножение): Например: На автостоянке стоят «Мерседес» и «Жигули» . Таблица истинности А - На автостоянке стоят «Жигули» В - На автостоянке стоит «Мерседес» А В 0 0 1 1 1 A&B

1. Конъюнкция (логическое умножение): Конъюнкция - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.
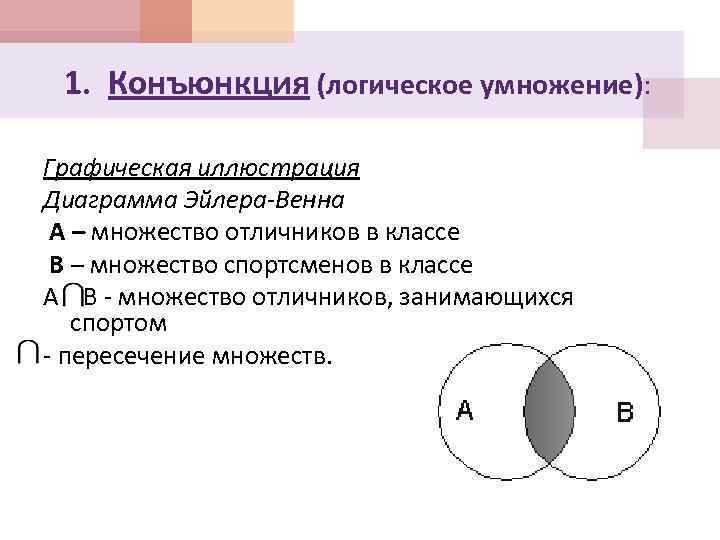
1. Конъюнкция (логическое умножение): Графическая иллюстрация Диаграмма Эйлера-Венна А – множество отличников в классе В – множество спортсменов в классе А В - множество отличников, занимающихся спортом - пересечение множеств.

2. Дизъюнкция (логическое сложение): Например: На автостоянке стоят «Мерседес» или «Жигули» . союз или; обозначение А B, А ИЛИ B, А+В в языках программирования обозначение Or.
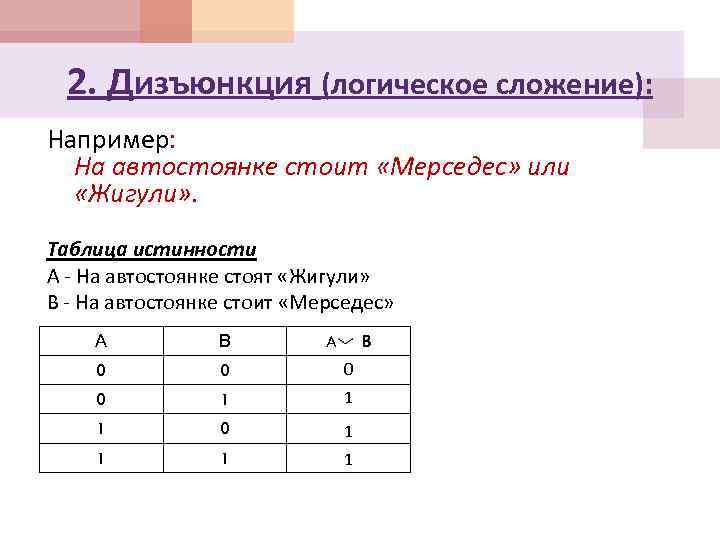
2. Дизъюнкция (логическое сложение): Например: На автостоянке стоит «Мерседес» или «Жигули» . Таблица истинности А - На автостоянке стоят «Жигули» В - На автостоянке стоит «Мерседес» А В 0 0 1 1 1 0 1 1 A B

2. Дизъюнкция (логическое сложение): Дизъюнкция - это логическая операция, которая каждым двум простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно.

2. Дизъюнкция (логическое сложение): Диаграмма Эйлера-Венна. А – множество отличников в классе В – множество спортсменов в классе А В - множество учеников класса, которые являются отличниками или спортсменами. - объединение множеств.

Строгая дизъюнкция : Например: На автостоянке стоят либо «Мерседес» либо «Жигули» . союз или; обозначение А B, в языках программирования обозначение Xor.
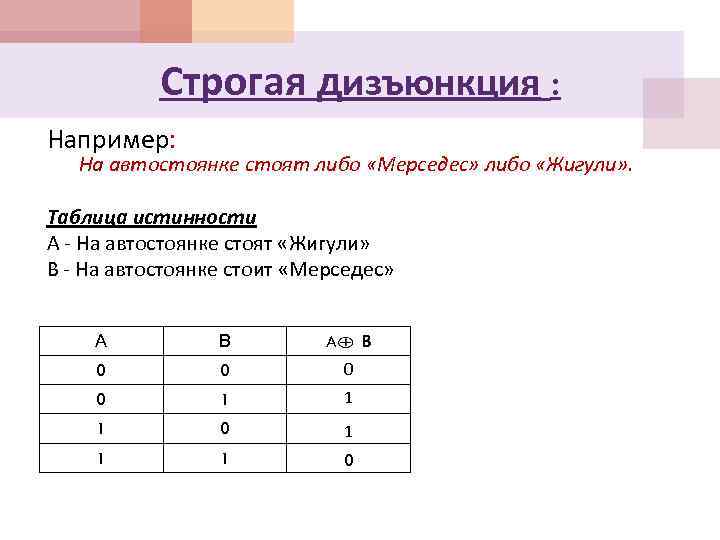
Строгая дизъюнкция : Например: На автостоянке стоят либо «Мерседес» либо «Жигули» . Таблица истинности А - На автостоянке стоят «Жигули» В - На автостоянке стоит «Мерседес» А В 0 0 1 1 1 0 A B

3. Инверсия (отрицание): Например: Я не знаю китайского языка. союз неверно, что. . . и частица не; обозначение , НЕ А. в языках программирования обозначение Not;

3. Инверсия (отрицание): Например: Я не знаю китайского языка. Таблица истинности А 0 1 1 0

3. Инверсия (отрицание): Отрицание - это логическая операция, которая каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается.

3. Инверсия (отрицание): Диаграмма Эйлера-Венна А – множество отличников в классе - множество не отличников в классе

4. Импликация (логическое следование): Например: Если число делится на 9, то оно делится на 3. соответствует оборотам речи если. . . , то. . . ; Обозначение =>

4. Импликация (логическое следование): Таблица истинности А В 0 0 1 1 1 08. 02. 2018 A=> B

4. Импликация (логическое следование): Импликация - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно.

5. Эквиваленция (логическое следование): Например: Земля мокрая тогда и только тогда, когда идет дождь. соответствует оборотам речи: тогда и только тогда; в том и только в том случае; Обозначения: , ~.
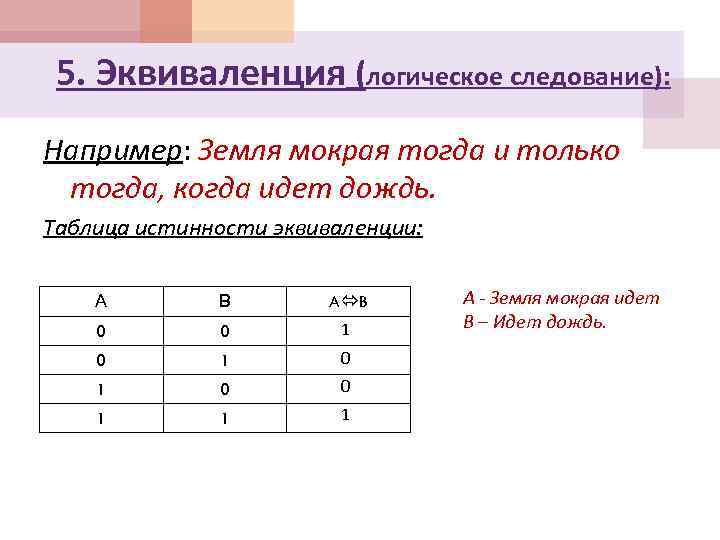
5. Эквиваленция (логическое следование): Например: Земля мокрая тогда и только тогда, когда идет дождь. Таблица истинности эквиваленции: А В A B 0 0 1 0 1 0 0 1 1 1 А - Земля мокрая идет В – Идет дождь.

5. Эквиваленция (логическое следование): Эквиваленция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.

Логические операции имеют следующий приоритет: Действия в скобках, Инверсия, Конъюнкция, Дизьюнкция, Импликация, Эквиваленция.

Домашнее задание: § 3. 2 записи в тетради решить задачи на карточках
2. Алгебра высказываний.pptx