07 11 12 Лекция 8 Предикатное программирование 7

07. 11. 12 Лекция 8 Предикатное программирование 7. Технология предикатного программирования 7. 4. Гиперфункции Неудобные ситуации в программировании Гиперфункция и оператор продолжения ветвей Свойства гиперфункций Пример. Вычисление суммы чисел в строке Пример. Решение системы линейных уравнений

7. Технология предикатного программирования 7. 4. Гиперфункции

Структурное программирование Эдвард Дейкстра begin <оператор1> ; <оператор2> end if <условие> then <оператор1> else <оператор2> end while <условие> do <оператор> end

Неудобные ситуации elem. Two(list(int) s: int e, bool exists ) { if (s = nil s. cdr = nil) exsts = false else { e = s. cdr. car || exists = true } } post exists = (s nil & s. cdr nil) & (exists e = s. cdr. car) elem. Two(s: e, exists); if (exists) B(e…) else D(…) (7. 13) if ( s = nil s. cdr = nil ) (7. 14) { exist = false; if (exist) B(e…) else D(…) } else {{e = s. cdr. car || exist = true }; if (exist) B(e…) else D(…)} if (s = nil s. cdr = nil) D(…) else { e = s. cdr. car; B(e…) }

Пример. Решение системы линейных уравнений Lin. Eq(a, x, b) type VEC(nat k) = array (real, 1. . k); type MATRICE(nat k) = array(real, 1. . k); Lin(nat n, MATRICE(n) a, VEC(n) b: VEC(n) x) pre det(n, a) 0 // > post Lin. Eq(n, a, x, b); Иногда требуется решить более общую задачу: Lin 1(nat n, MATRICE(n) a, VEC(n) b: bool c; VEC(n) x) post c = (det(n, a) 0) & (c Lin. Eq(n, a, x, b)); Lin 1(n, a, b: c; x); if (c) B(x…) else D(…)

P(x) { A(x: y, z, c) } c = C(x) Q(x, y, z); x, y и z возможно пустые Q(x, y, z) (C(x) S(x, y)) ( C(x) R(x, z)) (7. 16) Предикаты S(x, y) и R(x, z) функции S: x y и R: x z. C(x) истинно Q(x, y, z) совпадает с S: x y C(x) ложно Q(x, y, z) совпадает с R: x z. Q(x, y, z) результат склеивания функций S: x y и R: x z. В Q(x, y, z) не определено значение набора z, если C(x) истинно. Аналогично, не определено значение y при ложном C(x). Лемма 7. 10. Если предикат S(x, y) тотален в области P(x) & C(x), а R(x, z) в области P(x) & C(x), то спецификация предиката A(x: y, z, c) является тотальной. Лемма 7. 11. Если предикат S(x, y) является однозначным в области P(x) & C(x), а R(x, z) в области P(x) & C(x), то спецификация предиката A(x: y, z, c) является однозначной.

P(x) { A(x: y, z, c) } c = C(x) Q(x, y, z) (C(x) S(x, y)) ( C(x) R(x, z)) (7. 16) Пусть вызов A используется во фрагменте вида: A(x: y, z, c); if (c) B(y: u) else D(z: u) (7. 17) Построим оператор A’(x: y, z) модификацией A(x: y, z). Всякий оператор c = true заменим на #1, а c = false на #2. #1 и #2 обозначают операторы goto 1 и goto 2. A’(x: y, z); if (c) 1: B(y: u) else 2: D(z: u) (7. 18) A’(x: y, z); 1: B(y: u); goto 3; 2: D(z: u); 3: (7. 19) Предикат A’(x: y, z) будем записывать в виде A(x: y #1: z #2) и называть гиперфункцией с двумя ветвями. Метки 1 и 2 являются метками ветвей. A(x: y #1: z #2) case 1: B(y: u) case 2: D(z: u) (7. 20) Допускается более компактная запись: A(x: y : z) case B(y: u) case D(z: u) (7. 21)

Определение гиперфункции : A(x: y #1: z #2) pre P(x); pre 1: C(x) (7. 22) { A’(x: y, z) } post 1: S(x, y); post 2: R(x, z); Блок A’(x: y, z) тело гиперфункции, P(x) общее предусловие, C(x) предусловие первой ветви гиперфункции, S(x, y) постусловие первой ветви, R(x, z) постусловие второй ветви. Метки ветвей в определении предиката можно опустить: A(x: y: z ) pre P(x); pre 1: C(x) { … } … (7. 23) A(x: y #1: z #2) case 1: B(y: u) case 2: D(z: u) (7. 20) case 1: B(y: u) и case 2: D(z: u) операторы продолжения ветви, а вместе обработчик ветвей. Обработчику ветвей предшествует оператор, содержащий операторы перехода. Если предшествующий оператор нормально завершается (не оператором перехода), то обработчик ветвей пропускается.

elem. Two(list (int) s : int e : ) pre 1: s nil & s. cdr nil { if (s = nil s. cdr = nil) #2 else { e = s. cdr. car #1 } } post 1: e = s. cdr. car; elem. Two(list (int) s : int e #1 : #2) elem. Two(s: e: ) case B(e…) case D(…) elem. Two B(e…) D(…)

Пример 7. 4. Определим гиперфункцию Comp следующей спецификацией: Comp(list (int) s: : int d, list (int) r) pre 1: s = nil post 2: d = s. car & r = s. cdr; Построим определение предиката elem. Two через гиперфункцию Comp без полей car, cdr и конструктора nil. elem. Two(list (int) s: int e #1: #2) pre 1: s != nil & s. cdr != nil { int e 1; list (int) s 1, s 2; Comp(s: : e 1, s 1) case #2 case { Comp(s 1: : e, s 2) case #2 case #1 } } post 1: e = s. cdr. car;

Если оператор продолжения ветви содержит только оператор перехода, то оператор перехода переносится в конец соответствующей ветви вызова гиперфункции. elem. Two(list (int) s: int e #1: #2) pre 1: s != nil & s. cdr != nil { Comp(s: #2: int e 1, list (int) s 1) case Comp(s 1: #2: e, list(int) s 2 #1); } post 1: e = s. cdr. car; Реализован перенос описаний локальных переменных e 1, s 1 и s 2 в позиции их определения. Если обработчик ветвей состоит из единственного оператора продолжения ветви, а предшествующий оператор не имеет нормального завершения исполнения, то обработчик ветвей вырождается. В этом случае оператор продолжения ветви устраняется, а находящийся в нем оператор композируется с предыдущим оператором в виде оператора суперпозиции. elem. Two(list (int) s: int e #1: #2) pre 1: s != nil & s. cdr != nil { Comp(s: #2: _, list (int) s 1); Comp(s 1: #2: e, _ #1); } post 1: e = s. cdr. car; Вхождения локальных переменных e 1 и s 2 заменены стандартным именем “_”, означающим, что результат игнорируется при исполнении.

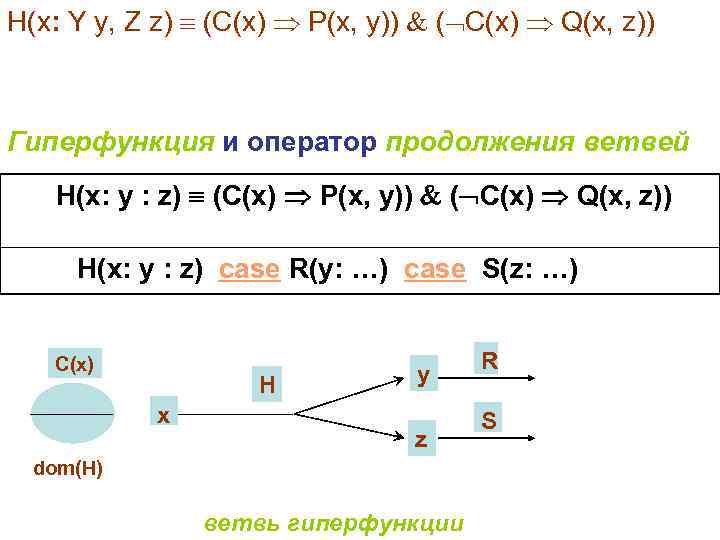H(x: Y y, Z z) (C(x) P(x, y)) ( C(x) Q(x, z)) Гиперфункция и оператор продолжения ветвей H(x: y : z) (C(x) P(x, y)) ( C(x) Q(x, z)) H(x: y : z) case R(y: …) case S(z: …) C(x) H x y z dom(H) ветвь гиперфункции R S

Свойства гиперфункций if ( (x)) { A; B } else { C; D } H(x…: … : …) case B case D H(X x…: … : …) { if ( (x)) {A #1} else {C #2} } моделирует механизм исключений

Пример. Сумма чисел в строке Сумма. Строки(string s: nat n) post P(s, n); Предикат P(s, n) определяется рекурсивным образом. цифра(char c) c {’ 0’, ’ 1’, ’ 2’, ’ 3’, ’ 4’, ’ 5’, ’ 6’, ’ 7’, ’ 8’, ’ 9’}; число(string s) s nil & s 1, s 2 string c char (s = s 1 + c + s 2 цифра(c)) val(string s: nat n) pre число(s) post n значение числа s. P(string s, nat n) (s = nil n = 0) & & (число(s) n = val(s)) & ( s 1 string c char. цифра(c) & s = c + s 1 P(s 1, n)) & & ( s 1, s 2 string c char. цифра(c) & число(s 1) & s = s 1 + c + s 2 m. P(s 2, m) & n = val(s 1) + m) string есть list(char), а “+” обозначает конкатенацию строк.

Обобщение исходной задачи : Сумма(string s, nat m: nat n) post x. P(s, x) & n = m + x; Ввиду истинности Сумма. Строки(s: n) Сумма(s, 0: n) корректно следующее определение предиката: Сумма. Строки(string s: nat n) {Сумма(s, 0: n)} post P(s, n); Алгоритм: Находится первая цифра. Вычисляется число, начинающееся с этой цифры. Для оставшейся части строки действие алгоритма повторяется. При нахождении первой цифры возможна ситуация, когда строка не содержит цифр. Данную ситуацию обозначим предикатом: мусор(string s) s 1, s 2 string c char (s = s 1 + c + s 2 цифра(c)) В частности, предикат истинен для пустой строки. Определение первой цифры выражается гиперфункцией: первая. Цифра(string s: : char e, string r) pre 1: мусор(s) post 2: w. мусор(w) & s = w + e + r & цифра(e);

Отметим, что можно было бы использовать гиперфункцию вида: первая. Цифра 1(string s: : string r), где r начинается с первой цифры, однако в реализации это приведет к повторному доступу к одной и той же литере в строке. В практике типично решение: первая. Цифра 2(string s: char e, string r) Здесь отсутствие цифр в строке s кодируется некоторым значением e, отличным от цифры. Вред подобных трюков обычно проявляется для сложных программ. Решение в виде гиперфункции дает более короткую и эффективную программу. Вторая часть алгоритма выделение числа в строке и его вычисление представляется предикатом: число. Встроке(char e, string r: nat v, string t) pre цифра(e) post w. конец. Числа(r, w, t) & v = val(e + w); конец. Числа(r, w, t) r = w + t & (w = nil число(w)) & (t = nil цифра(t. car));

Сумма(string s, nat m : nat n) { первая. Цифра(s: : char e, string r) case n = m case {число. Встроке(e, r: nat v, string t); Сумма(t, m + v: n)} } post x. P(s, x) & n = m + x measure len(s); первая. Цифра(string s: : char e, string r) pre 1: мусор(s) { if (s = nil) #1 else if (цифра(s. car)) { r = s. cdr || e = s. car #2} else первая. Цифра(s. cdr: #1 : e, r #2) } } post 2: w. мусор(w) & s = w + e + r & цифра(e) measure len(s); число. Встроке(char e, string r: nat v, string t) pre цифра(e) post w. конец. Числа(r, w, t) & v = val(e + w); конец. Числа(r, w, t) r = w + t & (w = nil число(w)) & (t = nil цифра(t. car);

Чтобы получить хвостовую рекурсию для предиката число. Встроке необходимо ввести накопитель для вычисления значения очередного числа. Определим предикат: взять. Число(string r, nat p: nat v, string t) post w. конец. Числа(r, w, t) & val 1(w, p, v); val(s: n) pre число(s) post val 1(s, 0, n); formula val 1(stringw, nat p, n) = w = nil ? n = p : val 1(w. cdr, p 10 + val. D(w. car), n) где val. D(e) значение цифры e. Тогда корректно следующее определение предиката: число. Встроке(char e, string r: nat v, string t) pre цифра(e) { взять. Число(r, val(e): v, t) } post w. конец. Числа(r, w, t) & v = val(e + w); конец. Числа(r, w, t) r = w + t & (w = nil число(w)) & (t = nil цифра(t. car);

взять. Число(string r, nat p: nat v, string t) { if (r = nil) {v = p || t = r} else { {char b = r. car || string q = r. cdr}; if (цифра(b)) взять. Число(q, p 10 + val(b): v, t) else {v = p || t = q} } } post w. конец. Числа(r, w, t) & val 1(w, p, v) measure len(r);

Сумма: n m; s r, t; первая. Цифра: число. Встроке: взять. Число: s r; s r, t; s r, q, t; Склеивания замена на s для упрощения v p; Сумма. Строки(string s: nat n){Сумма(s, 0: n)}; Сумма(string s, nat n : nat n) { первая. Цифра(s: : char e, string s) case n = n case {число. Встроке(e, s: nat v, string s); Сумма(s, n + v: n)} } первая. Цифра(string s: : char e, string s) { if (s = nil) #1 else if (цифра(s. car)) { s = s. cdr || e = s. car #2} else первая. Цифра(s. cdr: #1 : e, s #2) } }

число. Встроке(char e, string s: nat v, string s) { взять. Число(s, val(e): v, s) } взять. Число(string s, nat v: nat v, string s) { if (s = nil) {v = v || s = s} else { {char b = s. car || s = s. cdr }; if (цифра(b)) взять. Число(s, v 10 + val(b): v, s) else {v = v || s = s} } }; Замена хвостовой рекурсии циклом. Удаляются операторы вида n = n. Удаляется оператор продолжения case n = n Сумма. Строки(string s: nat n){Сумма(s, 0: n)}; Сумма(string s, nat n : nat n) { for (; ; ) { первая. Цифра(s: #M 1 : char e, string s #2) case 2: {число. Встроке(e, s: nat v, string s); n = n + v} } M 1: }

первая. Цифра(string s: : char e, string s) { for (; ; ) { if (s = nil) #1 else {{ s = s. cdr || e = s. car}; if (цифра(e)) #2 else {} } } число. Встроке(char e, string s: nat v, string s) { взять. Число(s, val(e): v, s) } взять. Число(string s, nat v: nat v, string s) { for (; ; ) { if (s = nil) break else { {char b = s. car || s = s. cdr}; if (цифра(b)) v = v 10 + val(b) else break } } };

Подставим определения предикатов взять. Число и первая. Цифра на место вызовов. Проведем очевидные упрощения. Сумма(string s, nat n : nat n) { n = 0; for (; ; ) { if (s = nil) #M 1 else { e = s. car; s = s. cdr; if (цифра(e)) #2 else { } } } case 2: { число. Встроке(e, s: nat v, string s); n= n + v } } M 1: } число. Встроке(char e, string s: nat v, string s) { v = val(e); for (; ; ) { if (s = nil) break {char b = s. car || s = s. cdr}; if (цифра(b)) v = v 10 + val(b) else break } };

Поскольку внутренний цикл в теле предиката Сумма не имеет нормального выхода, можно заменить оператор #2 на break и убрать скобки оператора продолжения ветви. Подставим определение число. Встроке на место вызова. Сумма. Строки(string s: nat n) { n = 0; for (; ; ) { if (s = nil) return { char e = s. car || s = s. cdr }; if (цифра(e)) break } nat v = val(e); for (; ; ) { if (s = nil) break {char b = s. car || s = s. cdr }; if (цифра(b)) v = v 10 + val(b) else break } n = n + v } } (7. 38)

Кодирование строк Необходимо кодировать начальное значение строки s и текущее. Начальное состояние вырезка S[m. . p], текущее S[j. . p]. Массив S и величины j, m, p должны быть определены в программе, причем j переменная, а m и p могут быть константами. type STR = array (char, M. . N); STR S; int j = m; Значения границ M и N должны быть достаточными, т. е. M ≤ m, p, j ≤ N. Операции с последовательностью s кодируются следующим образом: s = nil → j > p s. car → S[j] s = s. cdr → j = j + 1

type STR = array (char, M. . N); (7. 39) STR S; nat n = 0; for (int j = m; ; ) { for (; ; ) { if (j > p) return char e = S[j]; j = j + 1; if (цифра(e)) break } nat v = val(e); for (; j <= p; ) { char b = S[j]; j = j + 1; if (цифра(b)) v = v 10 + val(b) else break } n = n + v } если строка s завершается цифрой, то проверка исчерпания строки реализуется дважды.

Имеется недостаток программы (7. 39): если строка s завершается цифрой, то проверка исчерпания строки реализуется дважды. Чтобы исправить недостаток, следует вместо предиката число. Встроке(e, r: v, t) использовать гиперфункцию число. Встроке 1(e, r: v 1: v 2, t), в которой первая ветвь реализуется при исчерпании входной строки r. Возможен другой более простой алгоритм. На очередном шаге вычисляется значение очередного числа в строке в виде предиката число. Встроке(s: v, t), где v значение очередного числа, а t остаток непустой строки s. Если первый элемент s не является цифрой, то v = 0. Реализация данного алгоритма дает более короткую программу, чем (7. 39), однако менее эффективную. По сравнению с (7. 39) лишними действиями являются операторы v = 0 и n = n + v для каждого символа, отличного от цифры.

int n=0, j=0; while (j < N) { e=S[j++]; w = 0; while (j < N && String. Is. Number(e)) { w = int. Parse(e) + w * 10; e = S[j++]; } n = n + w; }

Система линейных уравнений Lin. Eq(a, x, b) type VEC(nat k) = array (real, 1. . k); type MATR(nat k) = array(real, 1. . k); formula SUM(nat n, predicate(nat: real) f: real) = n=0? 0: SUM(n-1, f) + f(n); formula Lin. Eq(nat n, MATR(n) a, VEC(n) b, x) = forall i=1. . n. SUM( n, predicate(nat j: real) {a[i, j] * x[j]} ) = b[i]; Lin(nat n, MATR(n) a, VEC(n) b: VEC(n) x : ) pre 1: not det(a) 0 { Triangle. Matr(n, a, b: MATR(n) c, VEC(n) d : #2); Solution(n, c, d: VEC(n) x ) #1 } post 1: Lin. Eq(n, a, b, x); алгоритм Гаусса (метод Жордано)

formula post. Lin(nat n, MATR(n) a, VEC(n) b, MATR(n) c, VEC(n) d) = forall VEC(n) x, y. Lin. Eq(a, b, x) & Lin. Eq(c, d, y) x = y formula triangle(nat n, MATR(n) a) = ( i=1. . n. a[i, i] = 1) i, j=1. . n. (i > j a[i, j] = 0) Triangle. Matr(nat n, MATR(n)a, VEC(n) b: MATR(n) a’, VEC(n) b’ : ) pre n > 0 pre 1: det(a) != 0 { Jord(n, a, b, 1: a’, b’ : ) } post 1: post. Lin(n, a, b, a’, b’) & triangle(n, a’); Спецификация неоднозначна ! Для верификации Lin применяются правила RS 9 RS 13 для общего случая

formula tria. Col(nat n, k, MATR(n) a) = i=1. . k-1. (a[i, i] = 1) i = 1. . n, j=1. . k-1. (i > j a[i, j] = 0) Jord(nat n, MATR(n) a, VEC(n) b, nat k: MATR(n) a’, VEC(n) b’ : ) pre 1 k n & tria. Col(n, k, a) pre 1: det(a) != 0 { diag. El(n, a, b, k: MATR(n) c, VEC(n) d : #2); norm(n, k, c, d: MATR(n) e, VEC(n) f); subtr. Lines(n, k, e, f: MATR(n) g, VEC(n) h); if (k = n) { a’ = g || b’ = h #1 } else Jord(n, g, h, k + 1: a’, b’ #1 : #2) } post 1: post. Lin(n, a, b, a’, b’) & triangle(n, a’);

diag. El(nat n, MATR(n) a, VEC(n) b, nat k: MATR(n) a’, VEC(n) b’ : ) pre 1 k n & tria. Col(n, k, a) pre 1: det(a) != 0 { if (a[k, k] != 0) {a’ = a || b’ = b #1} else perm(n, a, b, k, k+1: a’, b’ #1 | #2) } post 1: a’[k, k] != 0 & post. Lin(n, a, b, a’, b’)

perm(nat n, MATR(n) a, VEC(n) b, nat k, m: MATR(n) a’, VEC(n) b’ : ) pre 1 k n & kn) #2 else if (a[m, k] != 0) { b’ = b for (j) {case k: b[m] case m: b[k]}; a’ = a for (i, j) {case (k, k. . n): a[m, j] case (m, k. . n): a[k, j]} #1 } else perm(n, a, b, k, m + 1: a’, b’ #1 : #2) } post 1: a’[k, k] != 0 & post. Lin(n, a, b, a’, b’)

norm(nat n, k, MATR(n) a, VEC(n) b: MATR(n) a’, VEC(n) b’) pre 1 k n & a[k, k] != 0 & tria. Col(n, k, a) { b’ = b for (j) {case k: b[k] / a[k, k] }; a' = a for (i, j) {case (k, k. . n): a[k, j] / a[k, k]} } post a’[k, k] = 1 & post. Lin(n, a, b, a’, b’) subtr. Lines(nat n, k, MATR(n) a, VEC(n) b: MATR(n) a’, VEC(n) b’) pre 1 k n & a[k, k] = 1 & tria. Col(n, k, a) { b’ = b for (i) {case k+1. . n: b[i] - b[k] a[i, k]}; a' = a for (i, j) {case (k+1. . n, k. . n): a[i, j] - a[k, j] a[i, k] } } post tria. Col(n, k+1, a) & post. Lin(n, a, b, a’, b’)

Solution(nat n, MATR(n) a, VEC(n) b: VEC(n) x ) pre n > 0 & triangle(n, a) { uni. Mat(n, a, b, n: VEC(n) x ) } post Lin. Eq(n, a, b, x) formula nul. Coll(nat n, k, MATR(n) a) = j=k+1. . n. i=1. . j-1. a[i, j] = 0 uni. Mat(nat n, MATR(n) a, VEC(n) b, nat k: VEC(n) x ) pre n > 0 & triangle(n, a) & nul. Col(n, k, a) { if (k = 1) x = b else { subtr. Col(n, a, b, k : MATR(n) c, VEC(n) d); uni. Mat(n, c, d, k-1: VEC(n) x ) } } post Lin. Eq(n, a, b, x)

subtr. Col(nat n, MATR(n) a, VEC(n) b, nat k: MATR(n) a’, VEC(n) b’) pre n > 0 & triangle(n, a) & nul. Col(n, k, a) { b’ = b for (i) {case 1. . k-1: b[i] - b[k] a[i, k]}; a' = a for (i, j) {case (1. . k-1, k): 0 } } post nul. Col(n, k-1, a) & post. Lin(n, a, b, a’, b’) На первом этапе трансформации реализуется склеивания. Lin: a <- c; b <- d, x; Triangle. Matr: a <- a’; b <- b’; Jord: a <- c, e, g, a’; b <- d, f, h, b’; diag. El: a <- a’; b <- b’; perm: a <- a’; b <- b’; norm: a <- a’; b <- b’; subtr. Lines: a <- a’; b <- b’; Solution: b <- x; uni. Mat: a <- c; b <- d, x; subtr. Col: a <- a’; b <- b’;

На втором этапе реализуется замена хвостовой рекурсии циклами. Результатом проведения двух этапов трансформации является следующая программа: Lin(nat n, MATR(n) a, VEC(n) b: VEC(n) b : ) { Triangle. Matr(n, a, b: MATR(n) a, VEC(n) b : #2); Solution(n, a, b: VEC(n) b ) #1 } Triangle. Matr(nat n, MATR(n) a, VEC(n) b: MATR(n) a, VEC(n) b : ); { Jord(n, a, b, 1: MATR(n) a, VEC(n) b : ) }

Jord(nat n, MATR(n) a, VEC(n) b, nat k: MATR(n) a, VEC(n) b : ) { for(; ; ) { diag. El(n, a, b, k: MATR(n) a, VEC(n) b : #2); norm(n, k, a, b: MATR(n) a, VEC(n) b); subtr. Lines(n, k, a, b: MATR(n) a, VEC(n) b); if (k = n) #1 else k = k + 1 } } diag. El(nat n, MATR(n) a, VEC(n) b, nat k: MATR(n) a, VEC(n) b : ) { if (a[k, k] != 0) #1 else perm(n, a, b, k, k+1: a, b #1 | #2) }

perm(nat n, MATR(n) a, VEC(n) b, nat k, m: MATR(n) a, VEC(n) b : ) { for(; ; ) { if (m>n) #2 else if (a[m, k] != 0) { b = b for (j) {case k: b[m] case m: b[k]}; a = a for (i, j) {case (k, k. . n): a[m, j] case (m, k. . n): a[k, j]} #1 } else m = m + 1 } } norm(nat n, k, MATR(n) a, VEC(n) b: MATR(n) a, VEC(n) b) { b = b for (j) {case k: b[k] / c[k, k] }; a = a for (i, j) {case (k, k. . n): a[k, j] / a[k, k]} }

subtr. Lines(nat n, k, MATR(n) a, VEC(n) b: MATR(n) a, VEC(n) b) { b = b for (i) {case k+1. . n: b[i] - b[k] a[i, k]}; a = a for (i, j) {case (k+1. . n, k. . n): a[i, j] - a[k, j] a[i, k] } } Solution(nat n, MATR(n) a, VEC(n) b: VEC(n) b ) { uni. Mat(n, a, b, n: VEC(n) b ) } uni. Mat(nat n, MATR(n) a, VEC(n) b, nat k: VEC(n) b ) { for(; ; ) { if (k = 1) return; subtr. Col(n, a, b, k : MATR(n) a, VEC(n) b); k = k - 1 } } subtr. Col(nat n, MATR(n) a, VEC(n) b, nat k: MATR(n) a, VEC(n) b) { b = b for (i) {case 1. . k-1: b[i] - b[k] a[i, k]}; a = a for (i, j) {case (1. . k-1, k): 0 } }

На третьем этапе проведем подстановку следующую серию подстановок тел определений на место вызовов: perm -> diag. El; subtr. Lines, norm, diag. El -> Jord -> Triangle. Matr -> Lin; subtr. Col -> uni. Mat -> Solution -> Lin;

Lin(nat n, MATR(n) a, VEC(n) b: VEC(n) b : ) { for(nat k = 1; ; k=k+1) { if (a[k, k] != 0) #M 1; nat m; for(m = k +1; ; m = m + 1) { if (m>n) #2; if (a[m, k] != 0) break } b = b for (j) {case k: b[m] case m: b[k]}; a = a for (i, j) {case (k, k. . n): a[m, j] case (m, k. . n): a[k, j]} M 1: b = b for (j) {case k: b[k] / c[k, k] }; a = a for (i, j) {case (k, k. . n): a[k, j] / a[k, k]} b = b for (i) {case k+1. . n: b[i] - b[k] a[i, k]}; a = a for (i, j) {case (k+1. . n, k. . n): a[i, j] - a[k, j] a[i, k] } if (k = n) break } for(nat k = n; k != 1; k = k - 1) { b = b for (i) {case 1. . k-1: b[i] - b[k] a[i, k]}; a = a for (i, j) {case (1. . k-1, k): 0 } } #1 }

Lin(nat n, MATR(n) a, VEC(n) b: VEC(n) b : ) { for(nat k = 1; ; k=k+1) { if (a[k, k] != 0) #M 1; nat m; for(m = k +1; ; m = m + 1) { if (m>n) #2; if (a[m, k] != 0) break } real t = b[k]; b[k] = b[m]; b[m] = t; for (nat j=k; k<=n; k=k+1) { t = a[k, j]; a[k, j] = a[m, j]; a[m, j] = t } M 1: b[k] = b[k] / c[k, k]; for (nat j=k; j<=n; j=j+1) a[k, j] = a[k, j] / a[k, k]; for (nat i=k+1; i<=n; i=i+1) b[i] = b[i] - b[k] a[i, k]; for (nat i=k+1; i<=n; i=i+1) for (nat j=k; j<=n; j=j+1) a[i, j] = a[i, j] - a[k, j] a[i, k]; if (k = n) break } for(nat k = n; k != 1; k = k - 1) { for (nat i=1; i

Нетривиальным является устранение неиспользуемых вычислений : Lin(nat n, MATR(n) a, VEC(n) b: VEC(n) b : ) { for(nat k = 1; ; k=k+1) { if (a[k, k] != 0) #M 1; nat m; for(m = k +1; ; m = m + 1) { if (m>n) #2; if (a[m, k] != 0) break } real t = b[k]; b[k] = b[m]; b[m] = t; for (nat j=k; k<=n; k=k+1) { t = a[k, j]; a[k, j] = a[m, j]; a[m, j] = t } M 1: b[k] = b[k] / c[k, k]; for (nat j=k+1; j<=n; j=j+1) a[k, j] = a[k, j] / a[k, k]; for (nat i=k+1; i<=n; i=i+1) b[i] = b[i] - b[k] a[i, k]; for (nat i=k+1; i<=n; i=i+1) for (nat j=k+1; j<=n; j=j+1) a[i, j] = a[i, j] - a[k, j] a[i, k]; if (k = n) break } for(nat k = n; k != 1; k = k - 1) for (nat i=1; i