05 -Expectations Hypothesis l Yield Curve l Expectations

05 -Expectations Hypothesis l. Yield Curve l Expectations Theory 1

Yield Curve l All default-free bonds do not have the same growth rates, or YTM’s. l Bonds with different maturities have different YTM’s. l Yield Curve: a plot with – – 2 time-to-maturity on the x-axis YTM on y-axis.

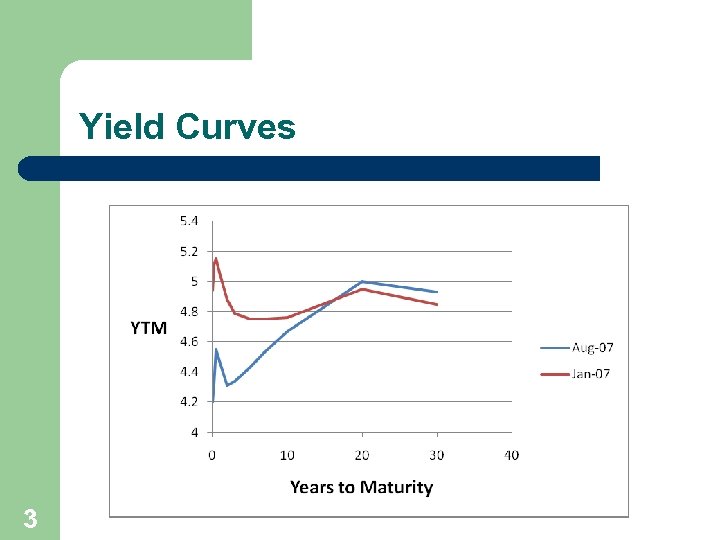Yield Curves 3

Term Structure Theory l The Big Picture: l Why don’t default-free bonds of different maturities grow at the same rate? l What defines the shape of the yield curve? – – 4 Why does the slope change? Why does it usually slope upwards?

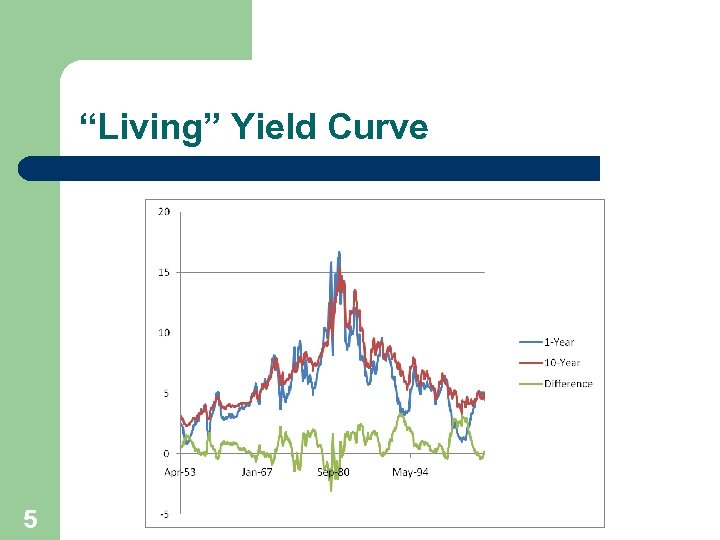“Living” Yield Curve 5

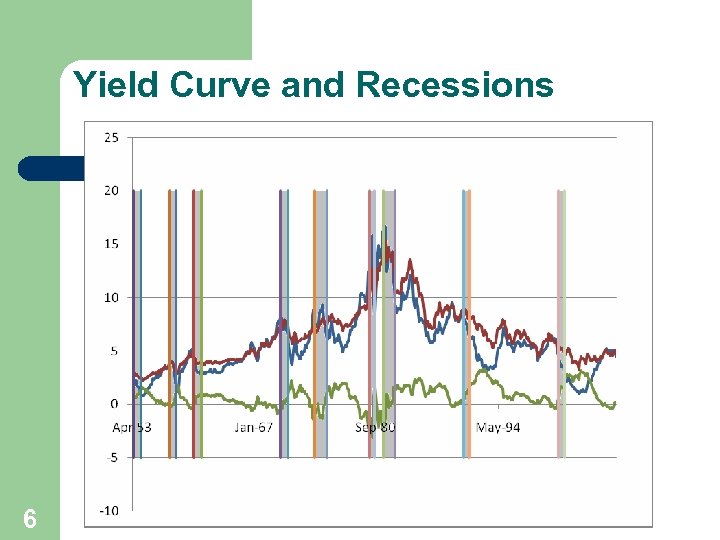Yield Curve and Recessions 6

Forward Rates l l Example: Current YTM on 1 -yr zero is 7%. Current YTM on 2 -yr zero is 8. 98% Consider two strategies: 1: Buy 1 -yr bond and roll over earnings at end of year to another 1 -yr zero-coupon bond 2: Buy a two year zero-coupon bond 7

Forward Rates Strategy 1: Invest in a one year bond and roll over 7% ? Strategy 2: Invest in a two year bond 8. 98% 8 8. 98%

Forward Rates l l 9 If we choose strategy 2, then we know for sure the growth rate of our money each year, provided we hold the bond to maturity. If we chose strategy 1, we don’t know exactly what we will earn over the second year because we don’t know exactly what bond prices (yields) will be at the end of the year.

Notation l YTMjt is the yield to maturity of a – – – l l 10 Zero coupon bond that matures in j years from time t. Is not completely observable until time t Time t is today, t+1 is next year, . . etc. The yield to maturity of a zero coupon bond is often referred to as the “spot” interest rate.

Notation l Examples: – – 11 1 -yr zero YTM 1 t is the YTM on a ____that matures ________ in one year from today. 2 -yr zero YTM 2 t is the YTM on a ____that matures in two years from today. ________ YTM 1 t+1 is the YTM on a 1 -yr zero _______that matures in two years from today. ________ 2 -yr zero YTM 2 t+2 is the YTM on a _______ that matures in four years from today. ________

Notation l Of course, we don’t know what yields (rates) will be when measured in the future. l We can develop some expectation – 12 is the expected YTM on a 1 -yr zero one year from now, that matures two years from now.

Forward Rates l l 13 Expected gross return from investing $1 in strategy 1 as of time t=1: E[R 1]=(1. 07)(1+ ) The gross return from investing $1 in strategy 2 (known as of time t=1). R 2=(1. 08)2

Forward Rates l l The expected gross returns must be close Suppose E[R 1] is much larger than R 2 – No one buys the two-year bond l – Everyone buys the one-year bond l l 14 Two year bond price drops, yield increases Price of one-year bond jumps, yield decreases Similar argument applies if R 2 is much larger than E[R 1]

Forward Rates l l 15 Suppose the expected gross returns are identical Then a forecast of one-year rate (YTM) in one year is

Forward Rates l In general, the gross returns of the two strategies should be close, but do not have to be equal. – l 16 Why might they differ? More on this later. . . No matter what is true in reality, we can always set the gross returns equal to each other, and solve for the rate that would need to prevail for the two strategies to be equal.

Forward Rates l l 17 Forward rates: the inferred short term rate of interest for a future period that makes the expected gross return of a long-term bond equal to that of rolling over short term bonds The two-year forward rate is 9%

Forward Rates l The n-period forward rate, solving for 18 , is found by

Example l Suppose as of time t: – – – 19 YTM on a 2 -year zero is 10% YTM on a 3 -year zero is 12% What is ?

Forward Rates l You can always lock in a future loan at the forward rate. l Example: YTM on 3 yr zero: 8% YTM on 4 yr zero: 10% What is 4 -year forward rate? 20 1. 083(1+f 4)=1. 104 or f 4=16. 22%

Forward Rates l Suppose you want to borrow $1000 three years from now to be paid back four years from now. How can you lock in at the 4 th year forward rate? – – Buy 1000/1. 083= 793. 83 in market value of 3 -year zeros Fund the purchase by borrowing 793. 83 at 10% due in four years. l 21 (Short-sell a bond)

Forward Rates l l In four years, your liability on the four year zeros has grown to 793. 83(1. 104)=1162. 25 l 22 In three years from now, the three year zeros provide you with a cash flow of 1000. This is 16. 22% higher than the cash received 1162. 25/1000 – 1 = 16. 22%

Expectations Theory l l 23 Expectations Theory: The gross return from investing in a long term bond is always equal to the expected return from rolling over short term bonds. For example:

Side Note: Geometric Mean l l 24 The mean of N random variables is The geometric mean is defined as

Side Note: Geometric Mean l Example with gross returns: 1. 1, 1. 05, . 95, 1. 02 – – l 25 Mean = 4. 12/4 = 1. 03 Geometric mean = (1. 1´ 1. 05´. 95´ 1. 02)1/4 = 1. 0285 For numbers close to 1, the geometric mean is approximately equal to the mean.

Expectations Theory l l 26 According to the Expectations Theory But the left side is a geometric mean, so to a close approximation,

Expectations Theory l l 27 But then In other words, the two period rate is approximately an average of the two oneperiod rates

Expectations Theory l This implies that – – – 28 if sloping, i. e. if then the yield curve is upward if sloping, i. e. then the yield curve is downward then the yield curve is flat, i. e.

Expectations Theory l l 29 What about longer term bonds? In general, the expectation theory says that the n-period spot rate equals the average of the one period rates expected to occur over the nperiod life of the bond.

Example l l Then l 30 Expected one-period spot rates A rising trend in expected short-term rates produces an upward sloping yield curve.