04 Geometric Progressions.pptx
- Количество слайдов: 55

04 Series

Today’s Objectives • Definition of a Geometric Progression (GP) • Formulae for the nth term and the sum of the first n terms • Consider the concept of convergence and divergence • The formula for the sum to infinity of a GP

Geometric Progressions (GPs) • A geometric progression is a sequence where each term is a constant multiple of the preceding term. • The constant multiple is known as the common ratio and we use the letter r. It can take any real value. • E. g. 12, 6, 3, 1. 5, 0. 75, … • This is a GP with first term 12 and common ratio of 0. 5

General term of a GP • The general formula for a term in a GP is: • Tn = arn-1 • where a is the first term, r is the common ratio and n is the position number

Sum of the 1 st n terms of a GP • Considering the sum of the first n terms of the sequence (i. e. the series), where a is the first term, r is the common ratio: • But as with the sum of an AP this is rather long so we use a similar approach to simplify this formula.

Sum of the 1 st n terms of a GP • We consider the same expression multiplied by r and then subtract one from the other:

Sum of the 1 st n terms of a GP • Hence, • If we do r. Sn – Sn instead we get, • Use the first if r < 1 and use the second if r > 1

Example 1 • The 5 th term of a GP is 8, the 3 rd term is 4, and the sum of the first ten terms is positive. Find the 1 st term, the common ratio, and the sum of the first ten terms. • We will find the 1 st term and common ratio simultaneously using the general term Tn = arn – 1. Then we will use the formula for Sn.

Example 1 solution • Since S 10 > 0 and the first term a > 0, then the common ratio r > 0:

Example 1 solution • Using a and r in the formula for the sum to n:

Example 2 • The sum of the first n terms of a series is 3 n – 1. Show that the terms in this series are in geometric progression and state the common ratio and the first term and the sum of the second set of n terms in this series. • If terms are in GP then there will be a constant common ratio and therefore Tn/Tn – 1 will be a constant and will be the common ratio. We can use Tn to state the first term. The sum of the second set on n terms will be given by S 2 n – Sn.

Example 2 solution • We need to find Tn and Tn – 1 and we are given S n:

Example 2 solution • Now consider whether Tn/Tn – 1 is a constant: • It is a constant and therefore the series is in GP and the common ratio is 3. • Now comparing our Tn = 3 n – 1(2) with the generalised Tn = arn – 1 and since r = 3 we conclude that the 1 st term a = 2.

Example 2 solution • Finally, finding the sum of the second set of n terms: • This method can be used to find the sum of any consecutive terms for an AP or GP, • e. g. S 8 – S 4 = T 5 + T 6 + T 7 + T 8

Example 3 • A prize fund is set up with a single investment of £ 2000 to provide an annual prize of £ 150. The fund accrues interest at 5% per year paid at the end of the year. If the first prize is awarded one year after the investment, find the number of years for which the full prize can be awarded. • We need to find an expression for the value of the prize fund after n years. We then use this formula to find the required value of n.

Example 3 solution • Let Pn is the amount in the prize fund at the end of n years. Then at the end of the first year:

Example 3 solution • So, at the end of the second year: • Using the same method, at the end of the third year:

Example 3 solution • Continuing this pattern, at the end of the nth year and simplifying:

Example 3 solution • Therefore: • Now Pn is the amount in the prize fund after the prize has been taken out. So we want to know the least value of n when Pn > 0 since if Pn > 0 then there was enough in the prize fund in the nth year.

Example 3 solution • So,
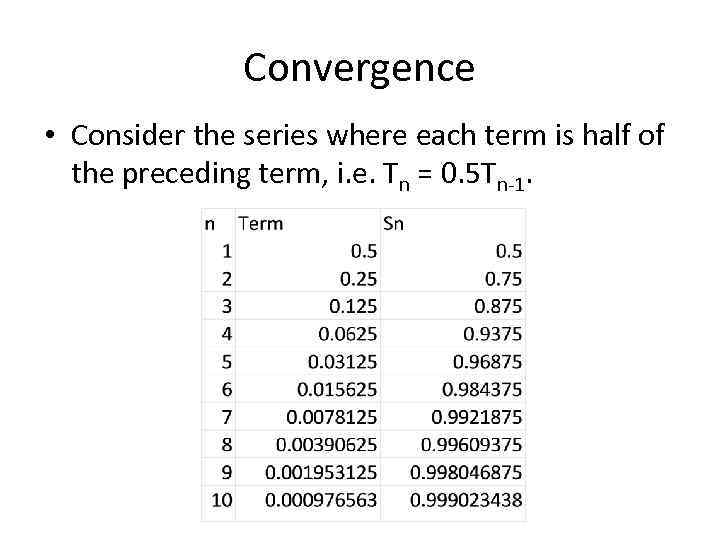
Convergence • Consider the series where each term is half of the preceding term, i. e. Tn = 0. 5 Tn-1.

Convergence • We can see that for this series the sum of the series converges to the value of 1. • This series is therefore convergent. • This series is actually a GP with first term a = 0. 5 and common ratio r = 0. 5.
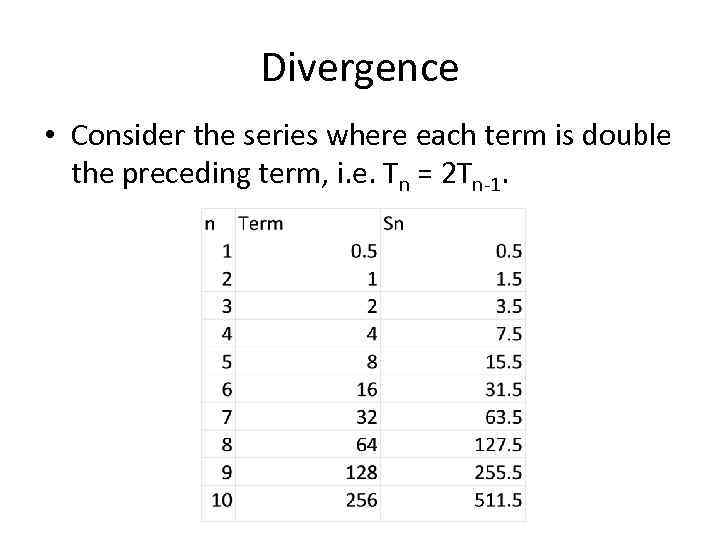
Divergence • Consider the series where each term is double the preceding term, i. e. Tn = 2 Tn-1.

Divergence • We can see that for this series the sum of the series continual increases and does not converge. • This series is therefore divergent. • This series is actually a GP with first term a = 0. 5 and common ratio r = 2.
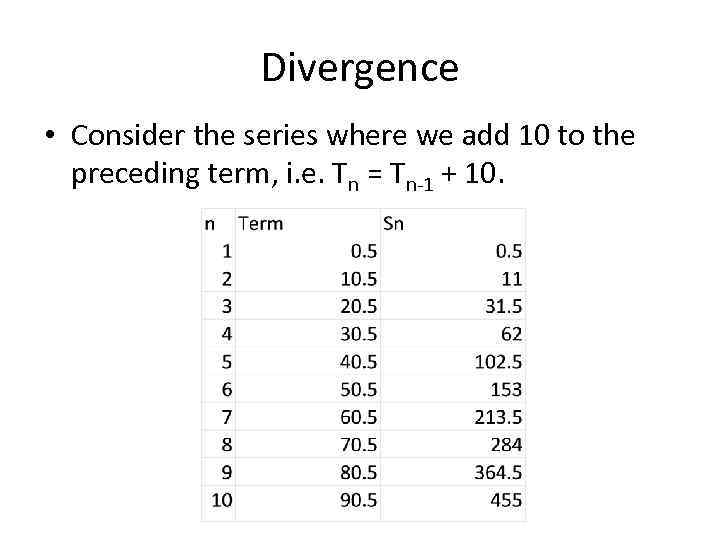
Divergence • Consider the series where we add 10 to the preceding term, i. e. Tn = Tn-1 + 10.

Divergence • We can see that for this series the sum of the series continual increases and does not converge. • This series is therefore divergent. • This series is actually an AP with first term a = 0. 5 and common difference d = 10.

Convergence and divergence • So we can generalise that all APs are divergent. • Also for GPs, – If |r| > 1 then the GP is divergent – If |r| < 1 then the GP is convergent

Sum to infinity of APs • Since, for an AP, we are continually adding or continually subtracting, as n increases so the sum to n increases or decreases depending on whether the common difference is positive or negative respectively. • So for an AP when n → ∞, • S∞ → ∞ when d > 0 • S∞ → –∞ when d < 0 • It is therefore not possible to find a formula for the sum to infinity for an AP.

Sum to infinity of GPs • The first two examples above were GPs but the first was convergent and the second was divergent. • For a divergent GP, i. e. |r|>1, then the sum to infinity will be infinite and so we can not find a formula for the sum to infinity. • However for a convergent GP, i. e. |r|<1, then it is possible to find a formula for the sum to infinity.

Sum to infinity of GPs • Consider the formula for the sum of the first n terms of a GP: • Now consider the value of rn as n → ∞ for |r| < 1 and for |r| > 1

Sum to infinity of GPs • For |r| < 1, i. e. – 1 < r < 1:

Sum to infinity of GPs • For |r| > 1, i. e. r < – 1 or r > 1:

Sum to infinity of a GP |r|<1 • Hence,

Example 4 • Determine if the following series converge or diverge and if possible find the sum to infinity: a. 3 + 5 + 7 +. . . b. 1 – ¼ + 1/16 – 1/64 +. . . c. 3 + 9/2 + 27/4 +. . . • To determine if a series converges or diverges, first establish if it is an AP or a GP then, if it is a GP, find the common ratio. Only if it is a GP with |r|<1, i. e. Convergent, can we find the sum to infinity.

Example 4 Solution a. 3 + 5 + 7 +. . . b. 1 – ¼ + 1/16 – 1/64 +. . .

Example 4 Solution c. 3 + 9/2 + 27/4 +. . .

Example 5 • Find the condition on x so that the following series converges: • Now evaluate the series when x = 1. 5.

Example 5 Solution • First we need to establish what type of series it is:

Example 5 Solution • The series will converge if |r| < 1:

Example 5 Solution • To evaluate the series when x = 1. 5 consider whether this value is within the range of convergence, i. e. is x = 1. 5 in the range – 1 < x < 3? • Since it is in the range of convergence and since we have not been told how many terms we must consider, we can use the formula for the sum to infinity.

Example 5 Solution • So,

Example 6 • Express the recurring decimal 0. 15 7 6 as a fraction in its lowest terms. • We can consider this recurring decimal as a sum and therefore as a series. This will allow us to convert it to a fraction.

Example 6 Solution • So,

Example 6 Solution • Now consider the term in the bracket:

Example 6 Solution • Simplifying:

Arithmetic mean • If 3 numbers, say p 1, p 2 and p 3, are in arithmetic progression the middle number p 2 is the arithmetic mean of p 1 and p 3. • Since if p 1 = a then p 2 = a + d and p 3 = a + 2 d then: • Hence the arithmetic mean of x and y is:

Geometric mean • If 3 numbers, say p 1, p 2 and p 3, are in geometric progression the middle number p 2 is the geometric mean of p 1 and p 3. • Since if p 1 = a then p 2 = ar and p 3 = ar 2 then: • Hence the geometric mean of x and y is:

Example 7 • The 3 rd term of a convergent GP is the arithmetic mean of the 1 st and 2 nd terms. Find the common ratio and, if the first term is 1, find the sum to infinity. • We should consider the general term of a GP and the corresponding 1 st, 2 nd and 3 rd term to find the common ratio. We can then use the formula for the sum to infinity.

Example 7 Solution • So,

Example 7 Solution • Now simplify and consider that the series is convergent:

Example 7 Solution • Now we know r and we are given that a = 1 so we can use the formula for the sum to infinity:

In summary • The general term of a GP is Tn = arn – 1 where a is the 1 st term, r is the common ratio and n is the position number. • The sum of the first n terms of a GP is given by: For r < 0 For r > 0

In summary • A series may be the sum or difference of an AP and a GP. • Therefore the sum to n of the whole series will be the sum or difference of the sum to n of the AP and the sum to n of the GP. • E. g. If the general term of a series is given by a 1 rn – 1 + a 2 + (n – 1)d • then Sn = a 1(1 – rn)/(1 – r) + n/2(a 2 + l)

In summary • A series is convergent if its sum approaches a specific value. • A series is divergent if its sum approaches (+/-) infinity. • All APs are divergent and so the sum to infinity is +/- infinity. • For GPs:

In summary • The arithmetic mean of x and y is: • The geometric mean of x and y is:
04 Geometric Progressions.pptx