0 Решение простейших тригонометрических неравенств. Алгебра и начала анализа, 10 класс. Воробьев Леонид Альбертович, г. Минск
Под простейшими тригонометрическими неравенствами понимают неравенства вида: , где t – выражение с переменной, a . Под знаком “ ” следует понимать любой из четырёх знаков неравенств: <, >, , .
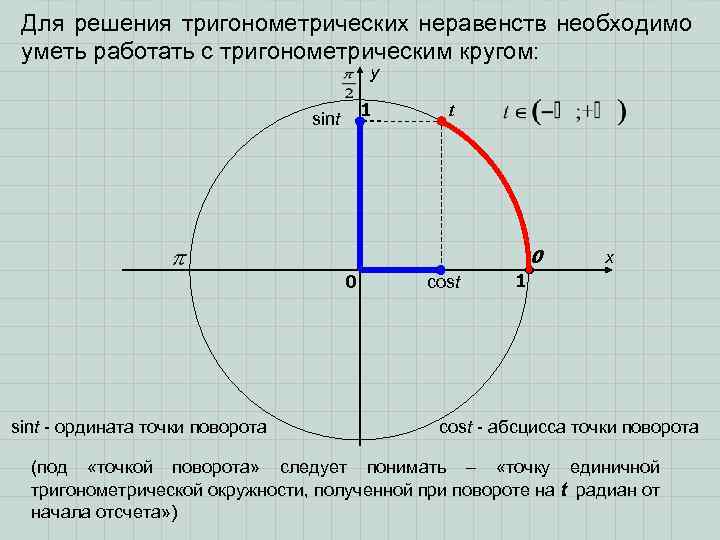
Для решения тригонометрических неравенств необходимо уметь работать с тригонометрическим кругом: y 1 sint t 0 0 sint - ордината точки поворота cost x 1 cost - абсцисса точки поворота (под «точкой поворота» следует понимать – «точку единичной тригонометрической окружности, полученной при повороте на t радиан от начала отсчета» )
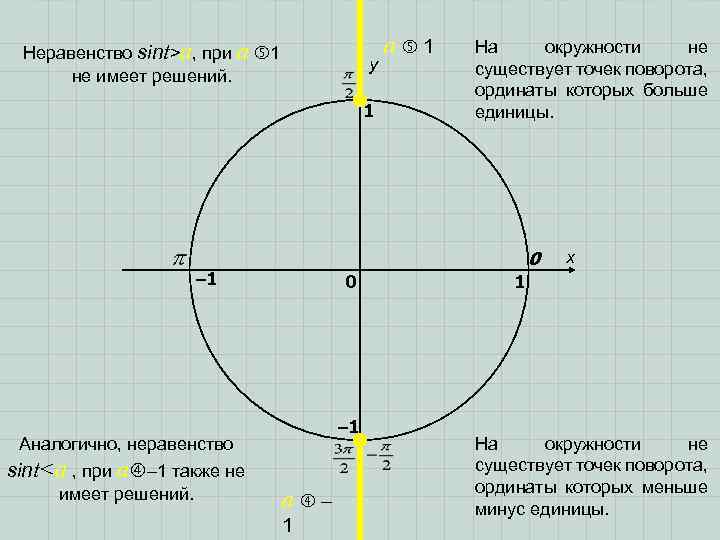
Неравенство sint>a, при a 1 не имеет решений. y 1 a 1 На окружности не существует точек поворота, ординаты которых больше единицы. 0 – 1 Аналогично, неравенство sint<a , при a – 1 также не имеет решений. a – 1 x 1 На окружности не существует точек поворота, ординаты которых меньше минус единицы.
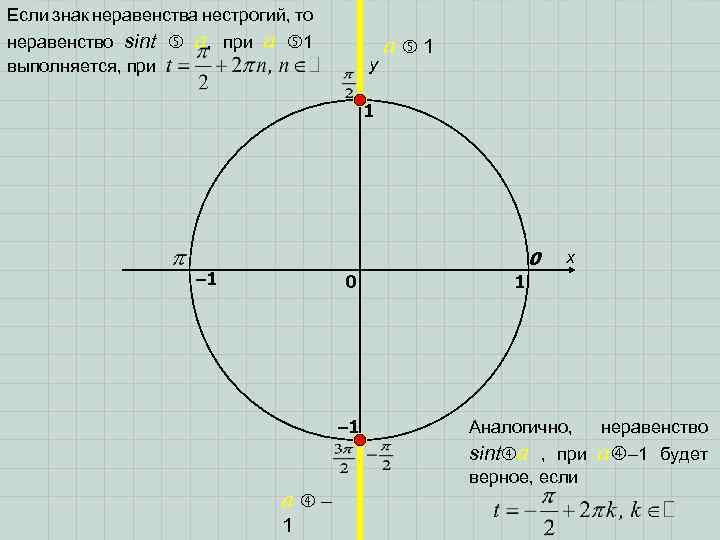
Если знак неравенства нестрогий, то неравенство sint выполняется, при a, при a 1 y a 1 1 0 – 1 x 0 – 1 1 Аналогично, неравенство sint a , при a – 1 верное, если будет
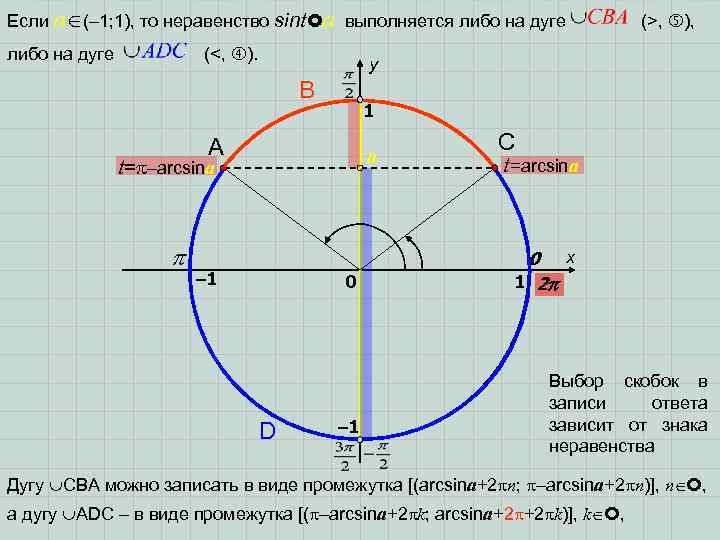
Если a (– 1; 1), то неравенство sint a выполняется либо на дуге (<, ). (>, ), y B 1 A a t= –arcsina – 1 0 D – 1 C t=arcsina 0 x 1 2 Выбор скобок в записи ответа зависит от знака неравенства Дугу CBA можно записать в виде промежутка [(arcsina+2 n; –arcsina+2 n)], n , а дугу ADC – в виде промежутка [( –arcsina+2 k; arcsina+2 +2 k)], k ,
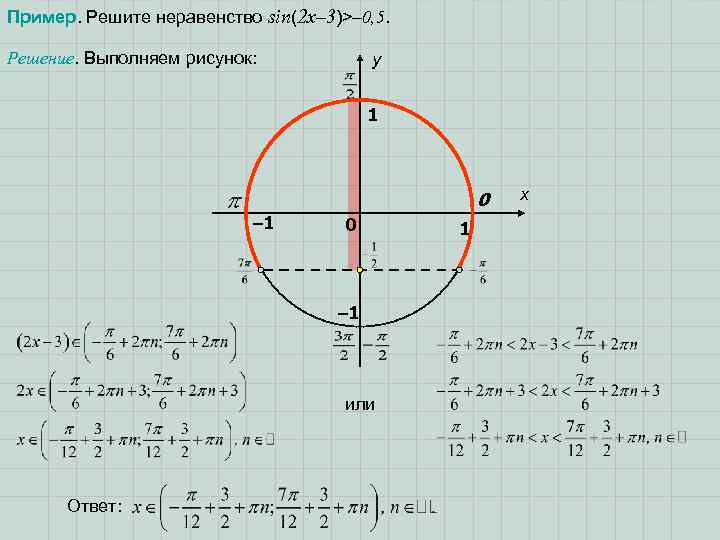
Пример. Решите неравенство sin(2 x– 3)>– 0, 5. Решение. Выполняем рисунок: y 1 0 – 1 или Ответ: 1 x
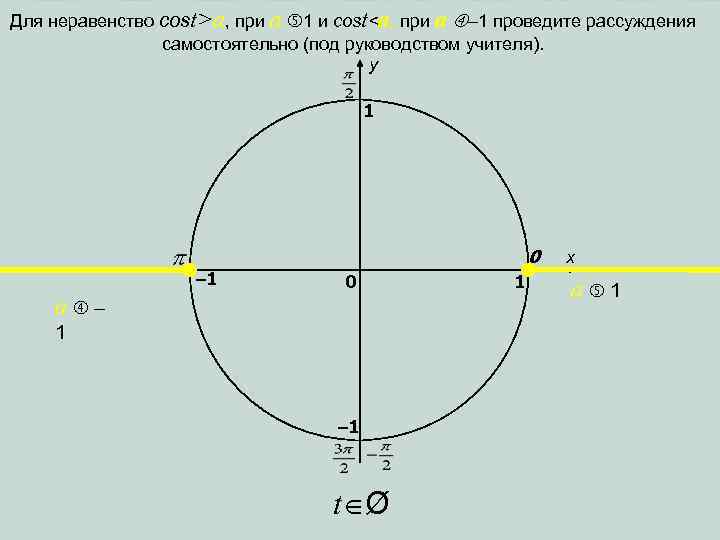
Для неравенство cost>a, при a 1 и cost<a, при a – 1 проведите рассуждения самостоятельно (под руководством учителя). y 1 0 – 1 0 a – 1 t Ø 1 x a 1
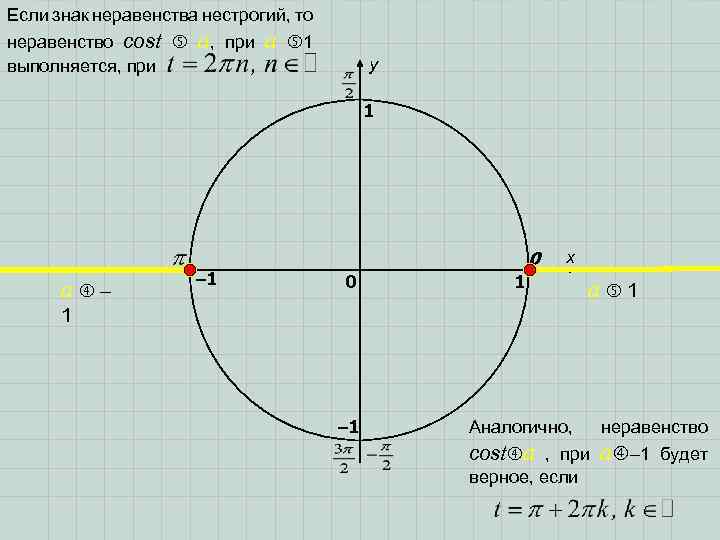
Если знак неравенства нестрогий, то неравенство cost выполняется, при a, при a 1 y 1 0 a – – 1 x 0 1 – 1 Аналогично, неравенство cost a , при a – 1 a 1 1 верное, если будет
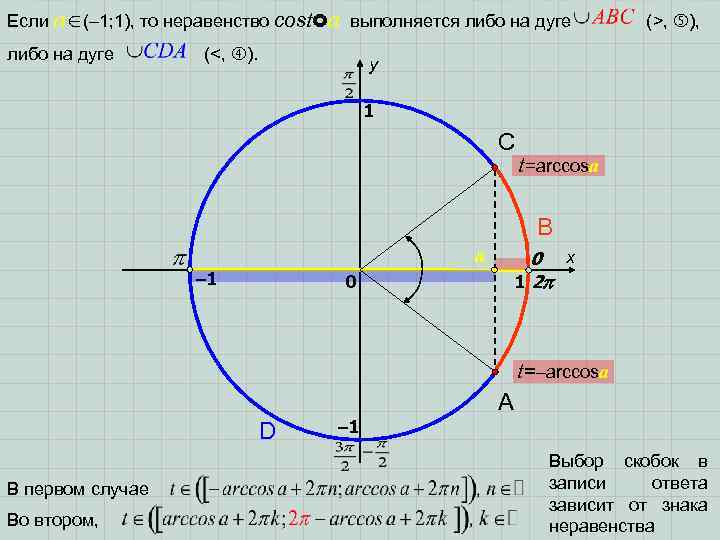
Если a (– 1; 1), то неравенство cost a выполняется либо на дуге (<, ). (>, ), y 1 C t=arccosa B a – 1 0 x 1 2 0 t=–arccosa A D В первом случае Во втором, – 1 Выбор скобок в записи ответа зависит от знака неравенства
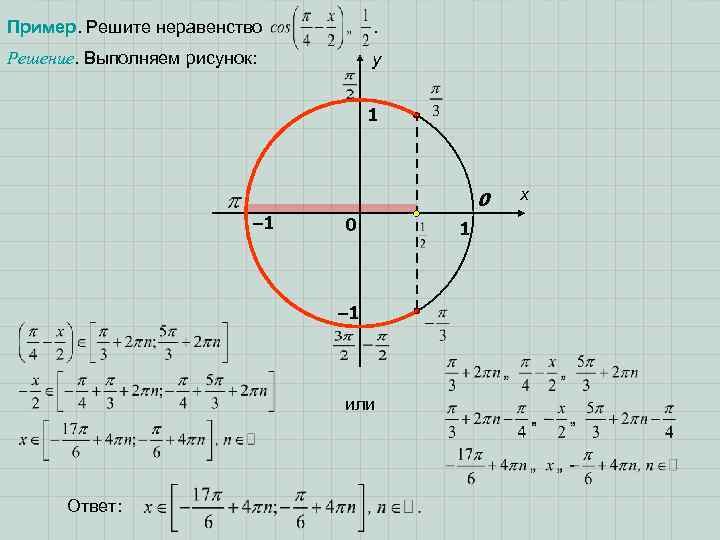
Пример. Решите неравенство . Решение. Выполняем рисунок: y 1 0 – 1 или Ответ: 1 x
Так как E(tg)= , то неравенство tgt a всегда имеет решение. линия тангенсов Значению tgt=a соответствуют числа t (величины углов поворота в радианной мере), попадающие в две точки тригонометрического круга. a y 1 Для неравенств tgt>a или tgt a получаем две дуги. Обе они могут быть записаны в виде промежутка: Для неравенств tgt<a или tgt a получаем две дуги. Обе они могут быть записаны в виде промежутка: t=arctga 0 – 1 t=arctga+π 0 – 1 Выбор скобок в записи ответа зависит от знака неравенства 1 0 x
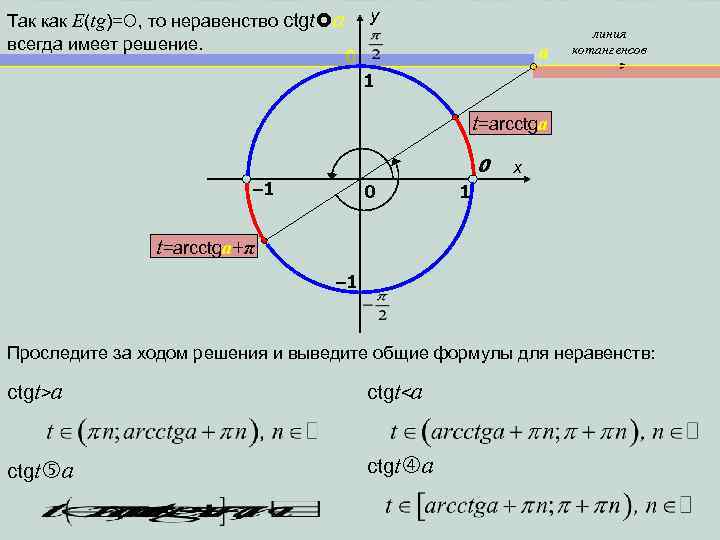
Так как E(tg)= , то неравенство сtgt a всегда имеет решение. y a 0 линия котангенсов 1 t=arcctga 0 – 1 0 x 1 t=arcctga+π – 1 Проследите за ходом решения и выведите общие формулы для неравенств: ctgt>a ctgt<a ctgt a
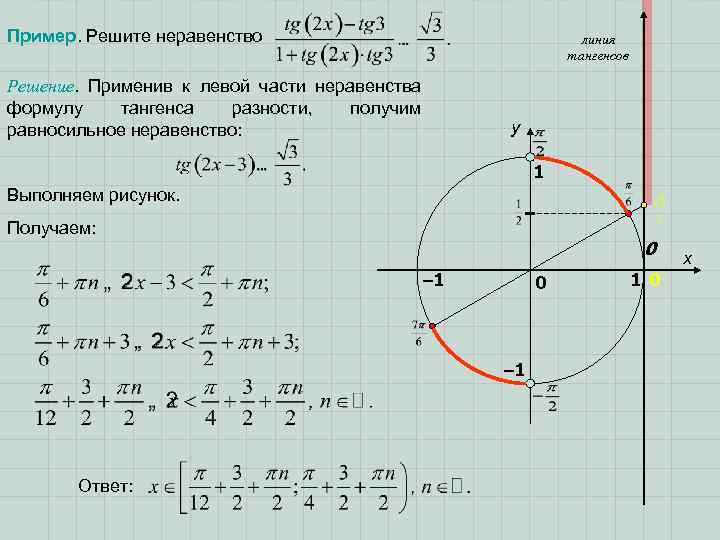
Пример. Решите неравенство линия тангенсов Решение. Применив к левой части неравенства формулу тангенса разности, получим равносильное неравенство: y 1 Выполняем рисунок. Получаем: 0 – 1 Ответ: 1 0 x
Скачать презентацию 0 Решение простейших тригонометрических неравенств Алгебра и начала
тригонометрия . новая тема! 24.11.2011.ppt