Scheduling_Theory.ppt
- Количество слайдов: 53
 0 Элементы теории расписаний Лектор: Сиднев Александр Георгиевич, доц. к. т. н. Слайд 1
0 Элементы теории расписаний Лектор: Сиднев Александр Георгиевич, доц. к. т. н. Слайд 1
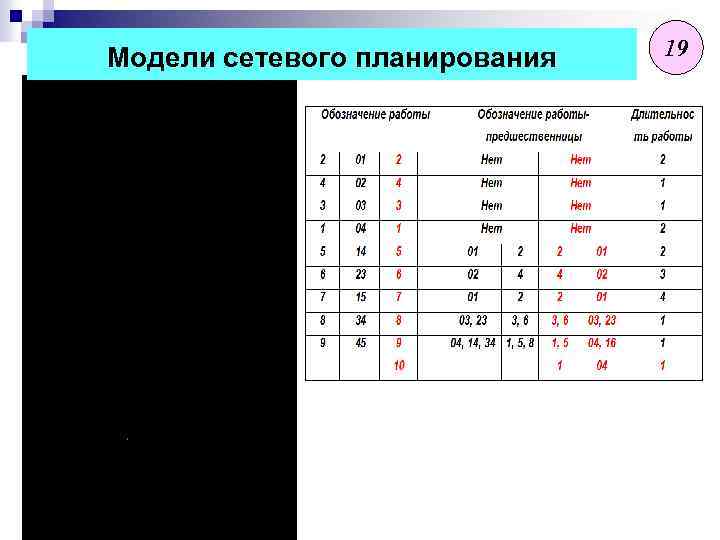
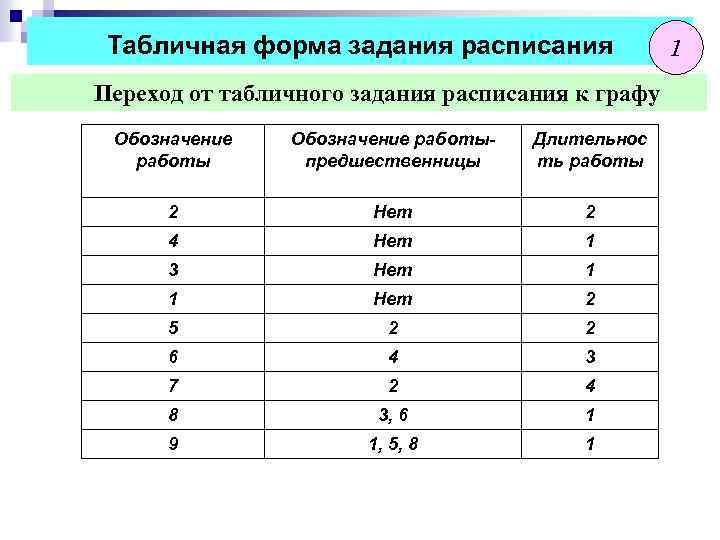 Табличная форма задания расписания Переход от табличного задания расписания к графу Обозначение работыпредшественницы Длительнос ть работы 2 Нет 2 4 Нет 1 3 Нет 1 1 Нет 2 5 2 2 6 4 3 7 2 4 8 3, 6 1 9 1, 5, 8 1 1
Табличная форма задания расписания Переход от табличного задания расписания к графу Обозначение работыпредшественницы Длительнос ть работы 2 Нет 2 4 Нет 1 3 Нет 1 1 Нет 2 5 2 2 6 4 3 7 2 4 8 3, 6 1 9 1, 5, 8 1 1
 Модели сетевого планирования Переход от табличного задания расписания к графу 2 варианта построения графа процесса 1. Узел – работа, дуга -- связь между работами Дуга определяет связь между данной работой и ее непосредственными предшественницами 2. Узел – событие, дуга – работа Событие считается совершенным, если выполнены все работы-дуги, входящие в узел-событие. работа-дуга может быть начата, если исходит из совершенного события 2
Модели сетевого планирования Переход от табличного задания расписания к графу 2 варианта построения графа процесса 1. Узел – работа, дуга -- связь между работами Дуга определяет связь между данной работой и ее непосредственными предшественницами 2. Узел – событие, дуга – работа Событие считается совершенным, если выполнены все работы-дуги, входящие в узел-событие. работа-дуга может быть начата, если исходит из совершенного события 2
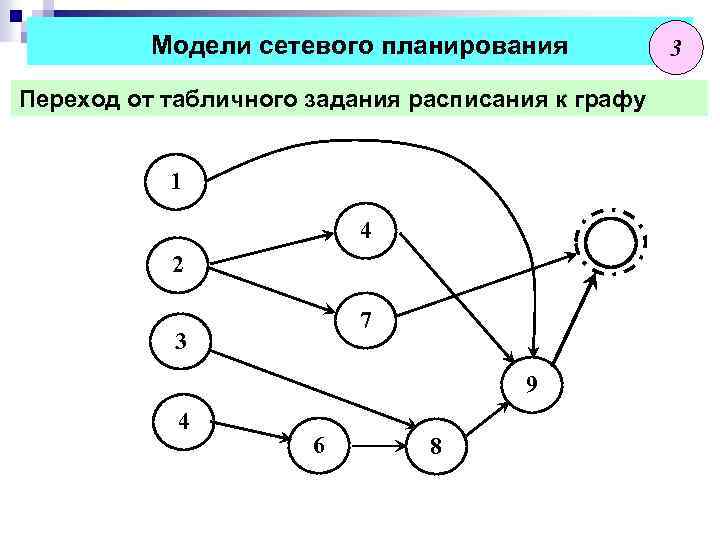 Модели сетевого планирования Переход от табличного задания расписания к графу 1 4 2 7 3 9 4 6 8 3
Модели сетевого планирования Переход от табличного задания расписания к графу 1 4 2 7 3 9 4 6 8 3
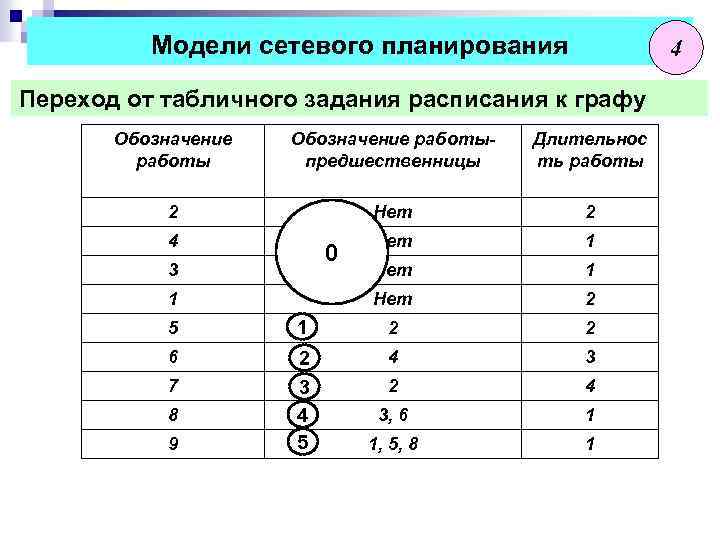 Модели сетевого планирования 4 Переход от табличного задания расписания к графу Обозначение работыпредшественницы Длительнос ть работы 2 Нет 2 4 Нет 1 Нет 2 0 3 1 5 1 2 2 6 2 3 4 5 4 3 2 4 3, 6 1 1, 5, 8 1 7 8 9
Модели сетевого планирования 4 Переход от табличного задания расписания к графу Обозначение работыпредшественницы Длительнос ть работы 2 Нет 2 4 Нет 1 Нет 2 0 3 1 5 1 2 2 6 2 3 4 5 4 3 2 4 3, 6 1 1, 5, 8 1 7 8 9
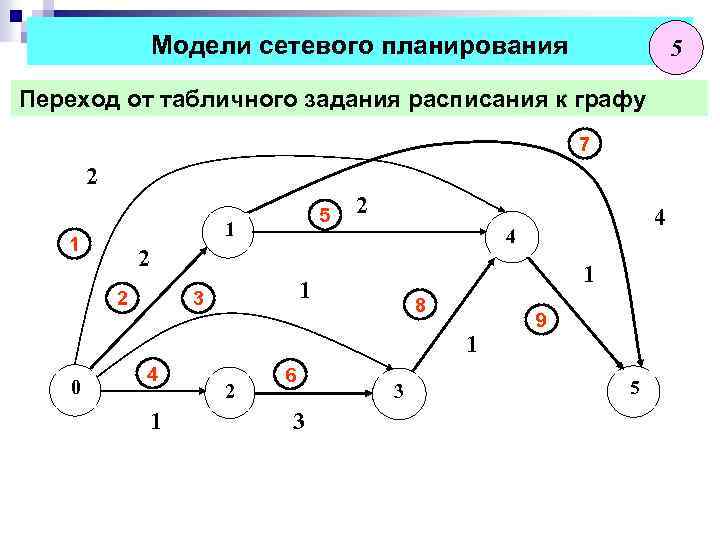 Модели сетевого планирования 5 Переход от табличного задания расписания к графу 7 2 5 1 1 1 2 2 2 1 1 3 8 1 4 0 0 1 1 2 2 6 3 3 4 4 4 3 3 9 5 5
Модели сетевого планирования 5 Переход от табличного задания расписания к графу 7 2 5 1 1 1 2 2 2 1 1 3 8 1 4 0 0 1 1 2 2 6 3 3 4 4 4 3 3 9 5 5
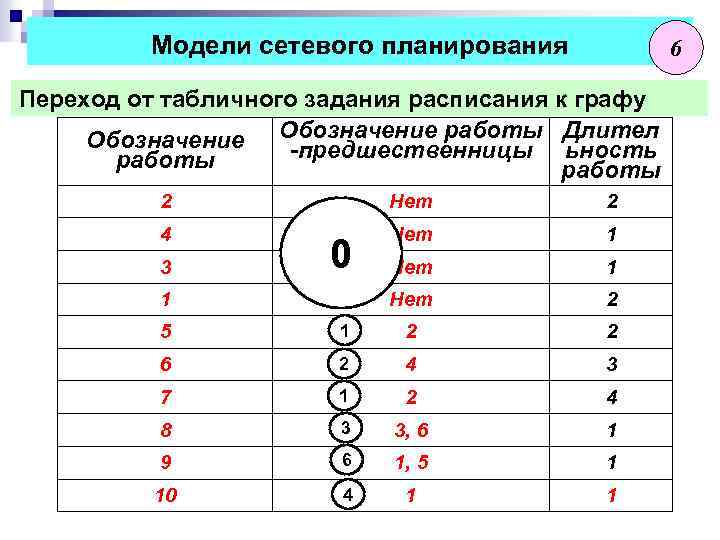 Модели сетевого планирования 6 Переход от табличного задания расписания к графу Обозначение работы Длител -предшественницы ьность работы 2 Нет 2 4 Нет 1 Нет 2 3 0 1 5 1 2 2 6 2 4 3 7 1 2 4 8 3 3, 6 1 9 6 1, 5 1 10 4 1 1
Модели сетевого планирования 6 Переход от табличного задания расписания к графу Обозначение работы Длител -предшественницы ьность работы 2 Нет 2 4 Нет 1 Нет 2 3 0 1 5 1 2 2 6 2 4 3 7 1 2 4 8 3 3, 6 1 9 6 1, 5 1 10 4 1 1
 Модели сетевого планирования 7 Переход от табличного задания расписания к графу Работа 1 является единственной непосредственной предшественницей работы 10 Работа 1 и работа 5 совместно являются непосредственными предшественниками работы 9 Таким образом, работа 1 порождает формирование двух событий: Событие 4: Завершение только работы 1 и Событие 6: Совместное завершение работ 1 и 5 При этом в ряде случаев приходится вводить фиктивные работы
Модели сетевого планирования 7 Переход от табличного задания расписания к графу Работа 1 является единственной непосредственной предшественницей работы 10 Работа 1 и работа 5 совместно являются непосредственными предшественниками работы 9 Таким образом, работа 1 порождает формирование двух событий: Событие 4: Завершение только работы 1 и Событие 6: Совместное завершение работ 1 и 5 При этом в ряде случаев приходится вводить фиктивные работы
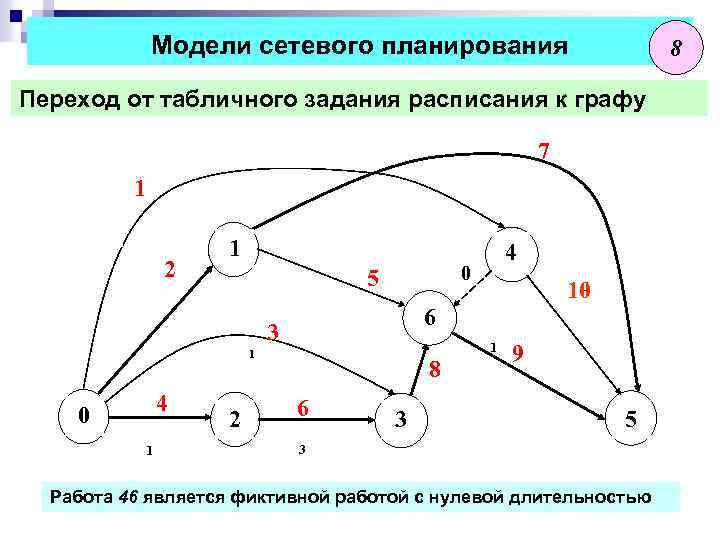 Модели сетевого планирования 8 Переход от табличного задания расписания к графу 7 1 2 1 1 0 5 1 1 4 1 2 2 1 10 6 3 0 0 4 4 4 8 6 3 3 9 5 5 3 Работа 46 является фиктивной работой с нулевой длительностью
Модели сетевого планирования 8 Переход от табличного задания расписания к графу 7 1 2 1 1 0 5 1 1 4 1 2 2 1 10 6 3 0 0 4 4 4 8 6 3 3 9 5 5 3 Работа 46 является фиктивной работой с нулевой длительностью
 Модели сетевого планирования Задача построения графа «узел – событие, дуга -- работа» Иногда приходится вводить фиктивные работы нулевой длительности Формальное правило построения графа с фиктивными работами вывести самостоятельно (желательно, см. Вентцель «Исследование операций» ) 9
Модели сетевого планирования Задача построения графа «узел – событие, дуга -- работа» Иногда приходится вводить фиктивные работы нулевой длительности Формальное правило построения графа с фиктивными работами вывести самостоятельно (желательно, см. Вентцель «Исследование операций» ) 9
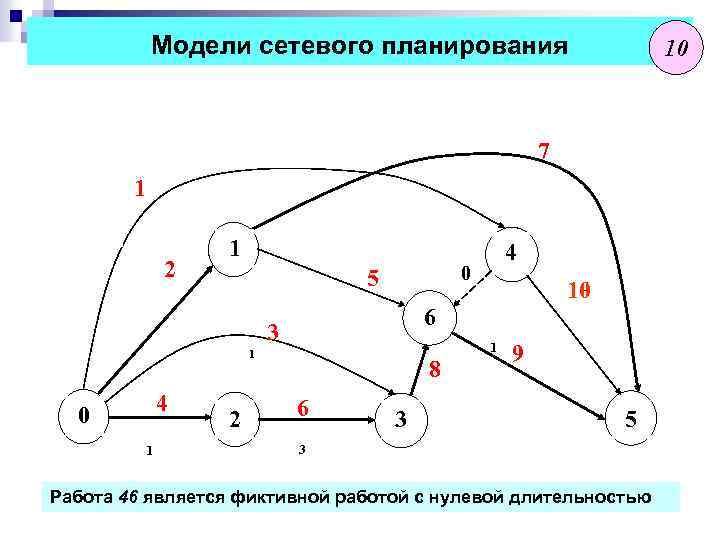 Модели сетевого планирования 10 7 1 2 1 1 0 5 1 1 4 1 2 2 1 10 6 3 0 0 4 4 4 8 6 3 3 9 5 5 3 Работа 46 является фиктивной работой с нулевой длительностью
Модели сетевого планирования 10 7 1 2 1 1 0 5 1 1 4 1 2 2 1 10 6 3 0 0 4 4 4 8 6 3 3 9 5 5 3 Работа 46 является фиктивной работой с нулевой длительностью
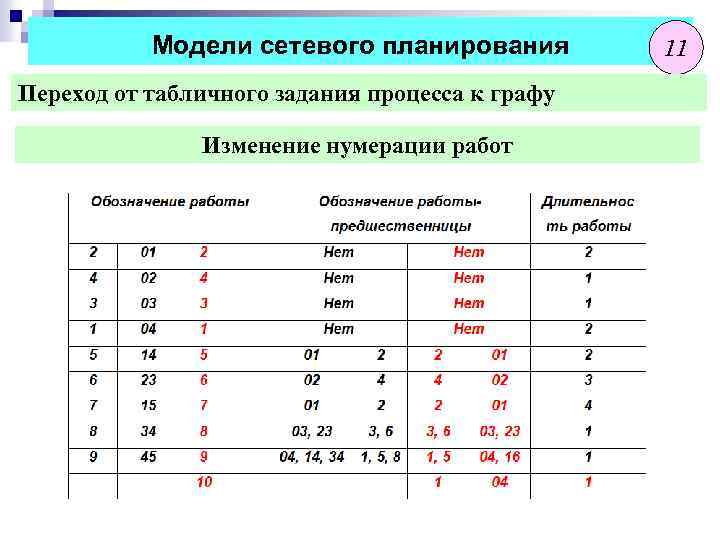 Модели сетевого планирования Переход от табличного задания процесса к графу Изменение нумерации работ 11
Модели сетевого планирования Переход от табличного задания процесса к графу Изменение нумерации работ 11
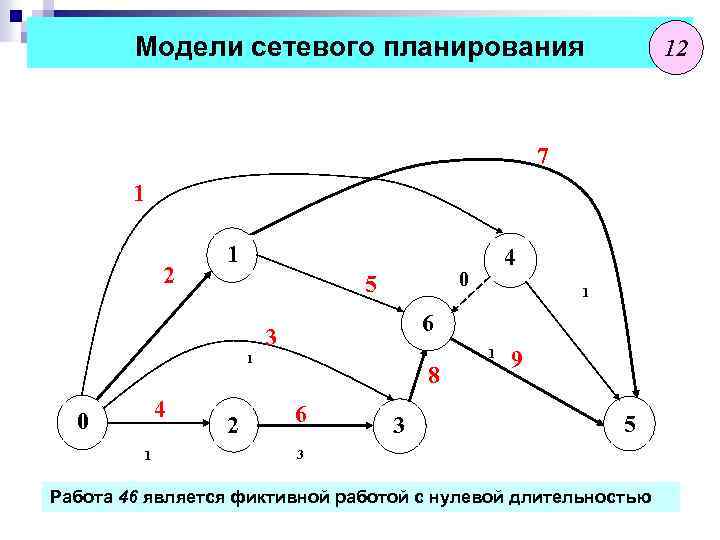 Модели сетевого планирования 12 7 1 2 1 1 0 5 1 1 4 1 2 2 1 6 3 0 0 4 4 4 8 6 3 3 9 5 5 3 Работа 46 является фиктивной работой с нулевой длительностью
Модели сетевого планирования 12 7 1 2 1 1 0 5 1 1 4 1 2 2 1 6 3 0 0 4 4 4 8 6 3 3 9 5 5 3 Работа 46 является фиктивной работой с нулевой длительностью
 Модели сетевого планирования Метод критического пути -Critical Path Method (CPM) Минимальное время выполнения бизнес-процесса – длина критического пути на графе 13
Модели сетевого планирования Метод критического пути -Critical Path Method (CPM) Минимальное время выполнения бизнес-процесса – длина критического пути на графе 13
 Модели сетевого планирования Математическое программирование для оценки показателей расписания -- длительность работы -- наиболее ранний момент начала работы условия, определяющие порядок выполнения работ 14
Модели сетевого планирования Математическое программирование для оценки показателей расписания -- длительность работы -- наиболее ранний момент начала работы условия, определяющие порядок выполнения работ 14
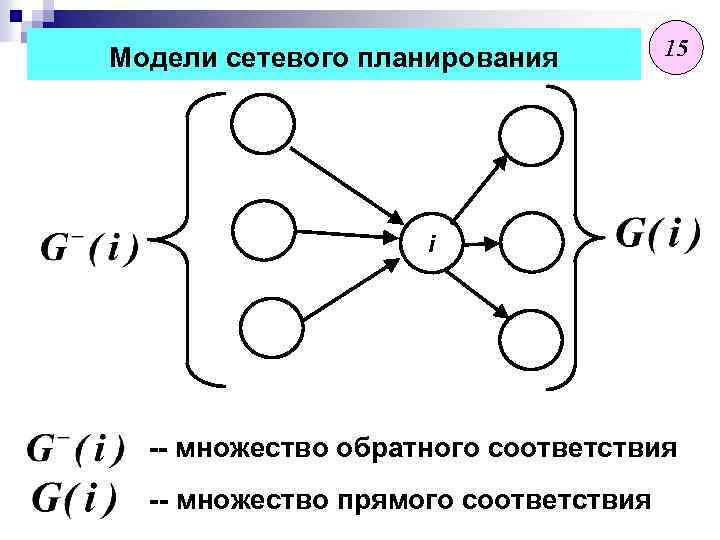 Модели сетевого планирования 15 i -- множество обратного соответствия -- множество прямого соответствия
Модели сетевого планирования 15 i -- множество обратного соответствия -- множество прямого соответствия
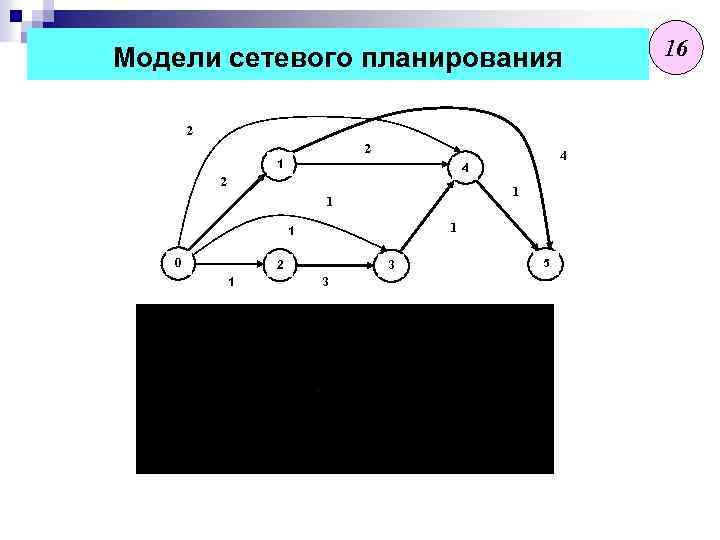 Модели сетевого планирования 2 2 1 1 1 1 0 0 2 11 4 4 3 3 5 5 16
Модели сетевого планирования 2 2 1 1 1 1 0 0 2 11 4 4 3 3 5 5 16
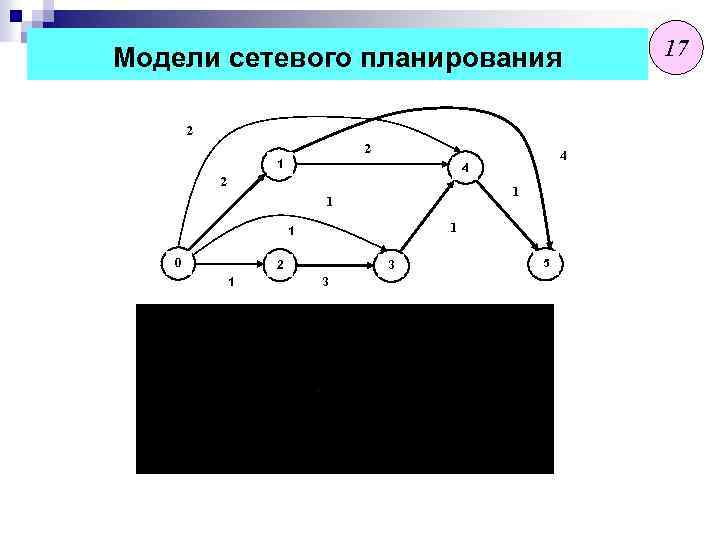 Модели сетевого планирования 2 2 1 1 1 1 0 0 2 11 4 4 3 3 5 5 17
Модели сетевого планирования 2 2 1 1 1 1 0 0 2 11 4 4 3 3 5 5 17
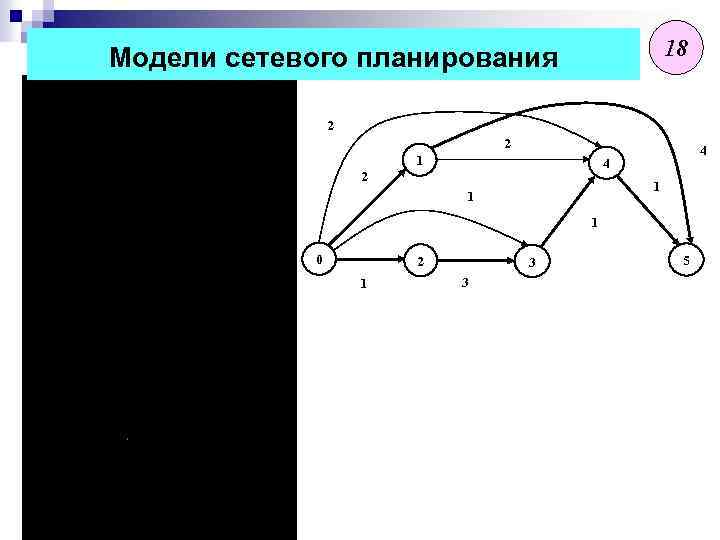 18 Модели сетевого планирования 2 2 1 4 4 2 1 1 1 0 0 2 1 3 3 5
18 Модели сетевого планирования 2 2 1 4 4 2 1 1 1 0 0 2 1 3 3 5
 Модели сетевого планирования 19
Модели сетевого планирования 19
 Элементы теории расписания 20 Динамическое программирование в задаче анализа расписания Условные обозначения: – время выполнения (длительность) работы ; – наиболее ранний момент осуществления -го события; – наиболее поздний момент осуществления -го события; – резерв времени выполнения работы .
Элементы теории расписания 20 Динамическое программирование в задаче анализа расписания Условные обозначения: – время выполнения (длительность) работы ; – наиболее ранний момент осуществления -го события; – наиболее поздний момент осуществления -го события; – резерв времени выполнения работы .
 Элементы теории расписания 21 Динамическое программирование в задаче анализа расписания
Элементы теории расписания 21 Динамическое программирование в задаче анализа расписания
 Элементы теории расписания 22 Динамическое программирование в задаче анализа расписания Процесс вычисления производится от начального узла к конечному Процесс вычисления производится от конечного узла к начальному
Элементы теории расписания 22 Динамическое программирование в задаче анализа расписания Процесс вычисления производится от начального узла к конечному Процесс вычисления производится от конечного узла к начальному
 Элементы теории расписания Виды резервов времени Полный резерв времени Независимый резерв времени 1 -го порядка Свободный резерв времени Независимый резерв времени 2 -го порядка 23
Элементы теории расписания Виды резервов времени Полный резерв времени Независимый резерв времени 1 -го порядка Свободный резерв времени Независимый резерв времени 2 -го порядка 23
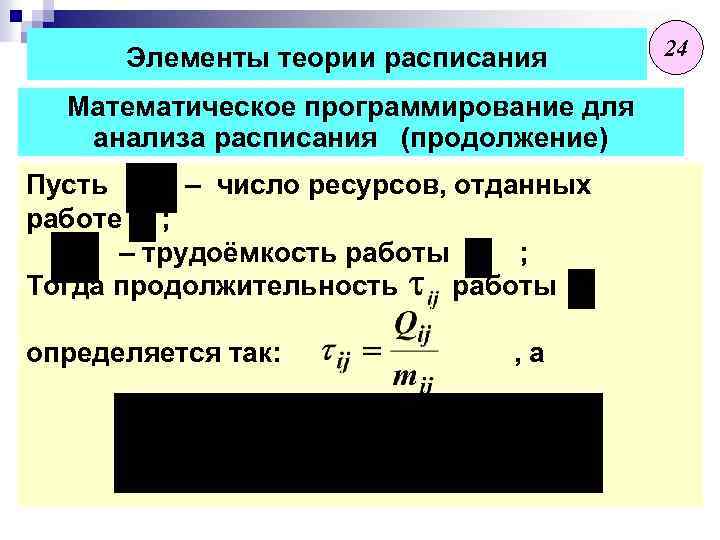 Элементы теории расписания Математическое программирование для анализа расписания (продолжение) Пусть – число ресурсов, отданных работе ; – трудоёмкость работы ; Тогда продолжительность работы определяется так: , а 24
Элементы теории расписания Математическое программирование для анализа расписания (продолжение) Пусть – число ресурсов, отданных работе ; – трудоёмкость работы ; Тогда продолжительность работы определяется так: , а 24
 Элементы теории расписания Математическое программирование для анализа расписания (продолжение) 25
Элементы теории расписания Математическое программирование для анализа расписания (продолжение) 25
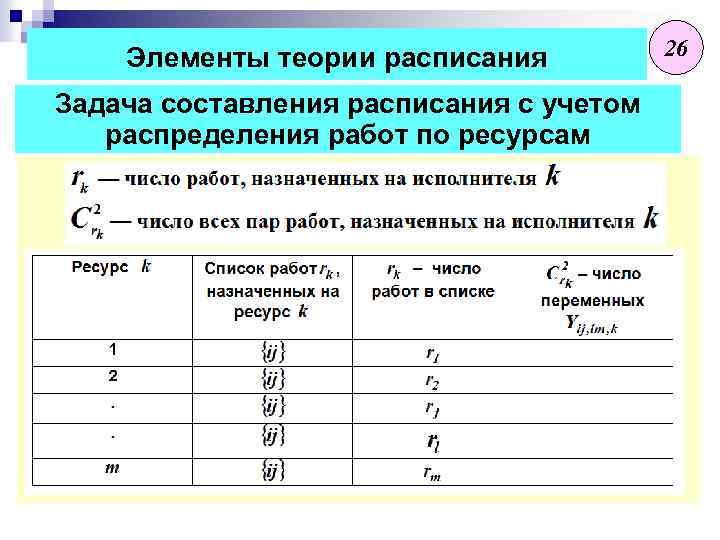 Элементы теории расписания Задача составления расписания с учетом распределения работ по ресурсам 26
Элементы теории расписания Задача составления расписания с учетом распределения работ по ресурсам 26
 Элементы теории расписания 27 Задача составления расписания с учетом распределения работ по ресурсам Бинарные переменные определяют порядок следования работ в паре
Элементы теории расписания 27 Задача составления расписания с учетом распределения работ по ресурсам Бинарные переменные определяют порядок следования работ в паре
 Элементы теории расписания Задача составления расписания с учетом распределения работ по ресурсам 28
Элементы теории расписания Задача составления расписания с учетом распределения работ по ресурсам 28
 Элементы теории расписания Задача составления расписания с учетом распределения работ по ресурсам 29
Элементы теории расписания Задача составления расписания с учетом распределения работ по ресурсам 29
 Элементы теории расписания Задача составления расписания с учетом распределения работ по ресурсам 30
Элементы теории расписания Задача составления расписания с учетом распределения работ по ресурсам 30
 Элементы теории расписания Задача составления расписания с учетом распределения работ по ресурсам 31
Элементы теории расписания Задача составления расписания с учетом распределения работ по ресурсам 31
 Элементы теории расписания 32 Вероятностные постановки задачи построения расписания Слабый разброс времён выполнения работ Критический путь не меняется!
Элементы теории расписания 32 Вероятностные постановки задачи построения расписания Слабый разброс времён выполнения работ Критический путь не меняется!
 Элементы теории расписания 33 Вероятностные постановки задачи построения расписания Слабый разброс времён выполнения работ
Элементы теории расписания 33 Вероятностные постановки задачи построения расписания Слабый разброс времён выполнения работ
 Элементы теории расписания 34 Вероятностные постановки задачи построения расписания Сильный разброс времён выполнения работ Критический путь может измениться! Один из подходов к решению задачи — использование методики GERT Graphical Evaluation and Review Technique
Элементы теории расписания 34 Вероятностные постановки задачи построения расписания Сильный разброс времён выполнения работ Критический путь может измениться! Один из подходов к решению задачи — использование методики GERT Graphical Evaluation and Review Technique
 Элементы теории расписания 35 Вероятностные постановки задачи построения расписания Сильный разброс времён выполнения работ Другой из подходов к решению задачи — использование имитационного моделирования (simulation) расписания — программная реализация процесса выполнения расписания, сопровождаемая сбором статистических данных
Элементы теории расписания 35 Вероятностные постановки задачи построения расписания Сильный разброс времён выполнения работ Другой из подходов к решению задачи — использование имитационного моделирования (simulation) расписания — программная реализация процесса выполнения расписания, сопровождаемая сбором статистических данных
 Элементы теории расписания 36 Исходные предпосылки моделирования расписания 1. Любая из работ начинается всегда, если • Выполнены все работы, от которых она зависит • Имеется свободный ресурс (исполнитель) 2. Все работы следует объединить в две группы: • Неконкурирующие работы (не создающие конфликта при назначении на ресурс) • Конкурирующие работы (претендующие на общий ресурс)
Элементы теории расписания 36 Исходные предпосылки моделирования расписания 1. Любая из работ начинается всегда, если • Выполнены все работы, от которых она зависит • Имеется свободный ресурс (исполнитель) 2. Все работы следует объединить в две группы: • Неконкурирующие работы (не создающие конфликта при назначении на ресурс) • Конкурирующие работы (претендующие на общий ресурс)
 Элементы теории расписания Исходные предпосылки моделирования расписания 37
Элементы теории расписания Исходные предпосылки моделирования расписания 37
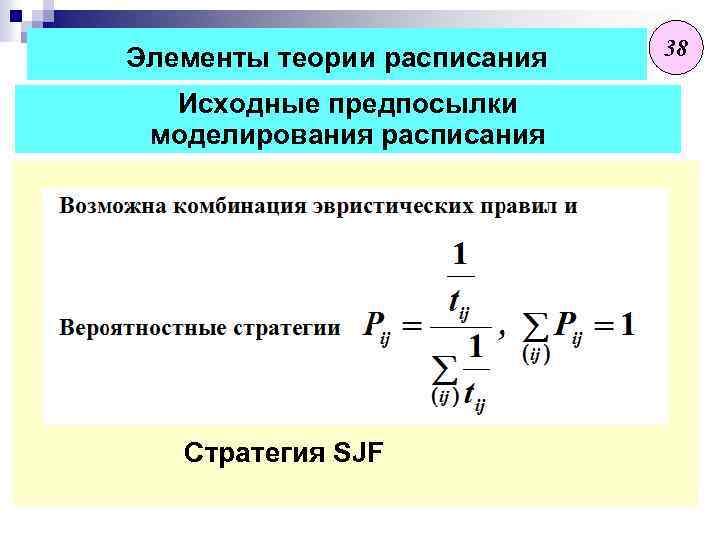 Элементы теории расписания Исходные предпосылки моделирования расписания Стратегия SJF 38
Элементы теории расписания Исходные предпосылки моделирования расписания Стратегия SJF 38
 Элементы теории расписания Исходные предпосылки моделирования расписания 39
Элементы теории расписания Исходные предпосылки моделирования расписания 39
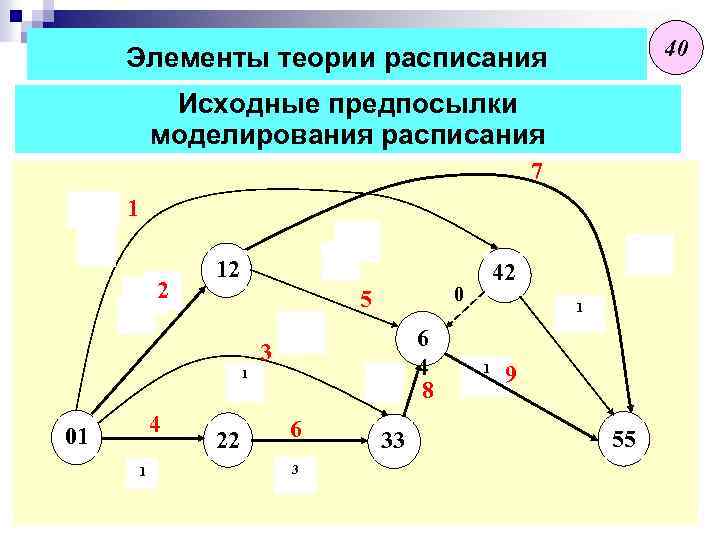 40 Элементы теории расписания Исходные предпосылки моделирования расписания 7 1 2 1 12 0 5 6 4 8 3 1 4 01 0 1 2 22 6 3 4 4 42 3 33 1 1 9 5 55
40 Элементы теории расписания Исходные предпосылки моделирования расписания 7 1 2 1 12 0 5 6 4 8 3 1 4 01 0 1 2 22 6 3 4 4 42 3 33 1 1 9 5 55
 Элементы теории расписания Алгоритм моделирования расписания 41
Элементы теории расписания Алгоритм моделирования расписания 41
 Элементы теории расписания Алгоритм моделирования расписания 42
Элементы теории расписания Алгоритм моделирования расписания 42
 Элементы теории расписания Алгоритм моделирования расписания 43
Элементы теории расписания Алгоритм моделирования расписания 43
 Элементы теории расписания Алгоритм моделирования расписания 44
Элементы теории расписания Алгоритм моделирования расписания 44
 Элементы теории расписания Алгоритм моделирования расписания 45
Элементы теории расписания Алгоритм моделирования расписания 45
 Элементы теории расписания Алгоритм моделирования расписания 45
Элементы теории расписания Алгоритм моделирования расписания 45
 Элементы теории расписания Алгоритм моделирования расписания 45
Элементы теории расписания Алгоритм моделирования расписания 45
 Элементы теории расписания Алгоритм моделирования расписания 45
Элементы теории расписания Алгоритм моделирования расписания 45
 Элементы теории расписания Алгоритм моделирования расписания 45
Элементы теории расписания Алгоритм моделирования расписания 45
 Элементы теории расписания Алгоритм моделирования расписания 45
Элементы теории расписания Алгоритм моделирования расписания 45
 Элементы теории расписания Алгоритм моделирования расписания 45
Элементы теории расписания Алгоритм моделирования расписания 45
 Элементы теории расписания Алгоритм моделирования расписания 45
Элементы теории расписания Алгоритм моделирования расписания 45


