c77a447a1534478a7e99ca4a05bf764f.ppt
- Количество слайдов: 49
3体散乱問題におけるカイラル有効場ポテンシャルと 3体力の計算 Kyushu Institute of Technology: H. Kamada Ruhr-Universitaet Bochum: W. Glöckle Jagiellonian University: Witala, Golak, R. Skibinski H. J. Bonn Universitaet: E. Epelbaum, Ulf-G. Meißner Forschungszentrum Juelich: A. Nogga 「少数粒子系物理の現状と今後の展望」 University of Iowa: W. N. Polyzou 大阪大学RCNP 2008年12月23日‐25日 N P P

Motivation: The nonrelativistic theoretical prediction of the Nd scattering cross section beyond 200 Me. V/u is getting to be poor even including the 3 -body force (FM type). What is missing?
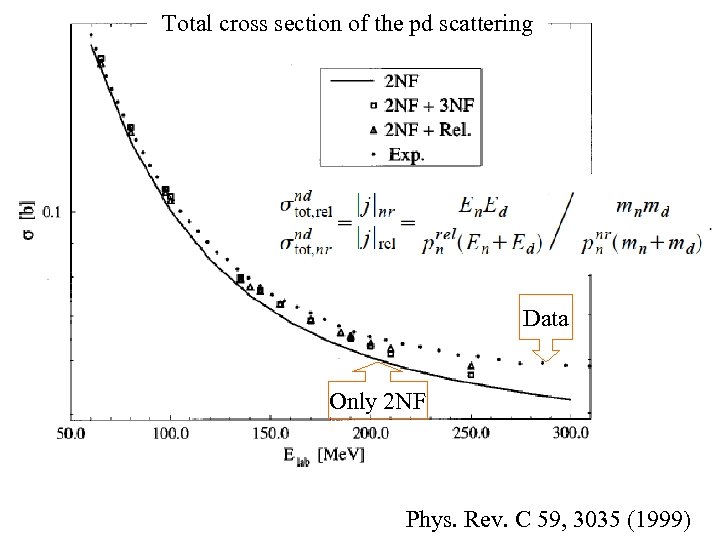
Total cross section of the pd scattering Data Only 2 NF Phys. Rev. C 59, 3035 (1999)
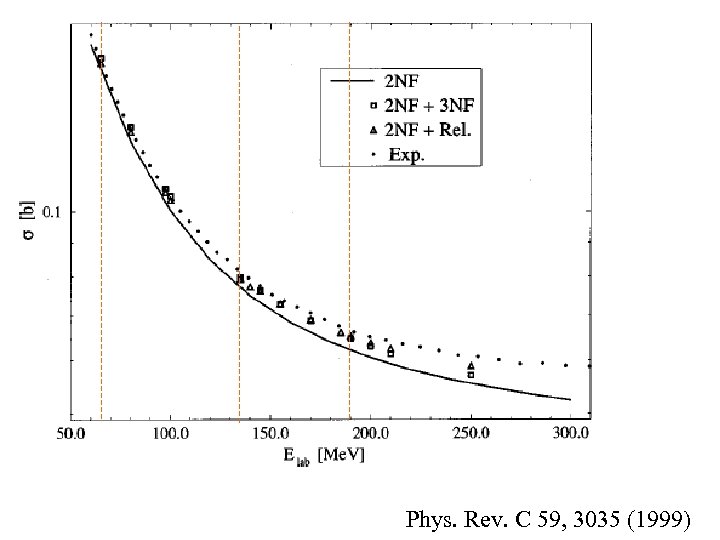
Phys. Rev. C 59, 3035 (1999)
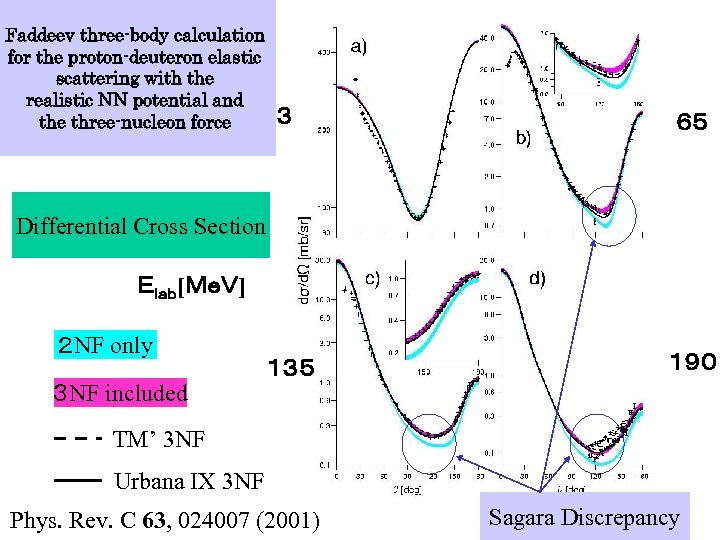
Faddeev three-body calculation for the proton-deuteron elastic scattering with the realistic NN potential and the three-nucleon force 3 65 135 190 Differential Cross Section Elab[MeV] 2 NF only 3 NF included TM’ 3 NF Urbana IX 3 NF Phys. Rev. C 63, 024007 (2001) Sagara Discrepancy
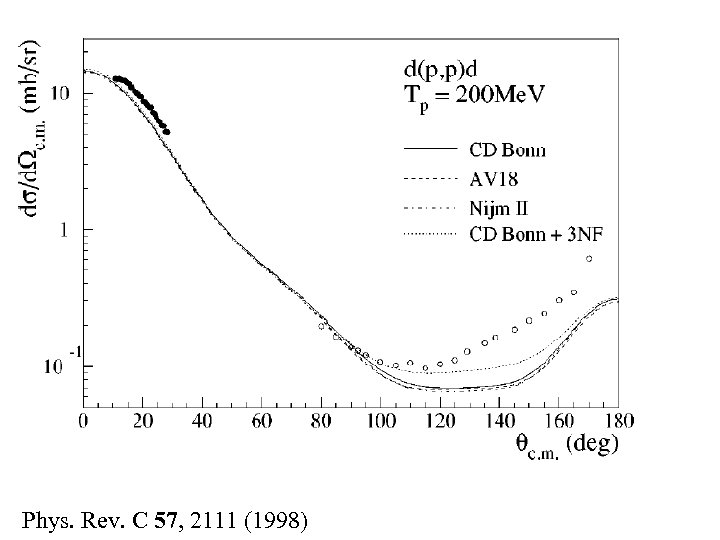
Phys. Rev. C 57, 2111 (1998)
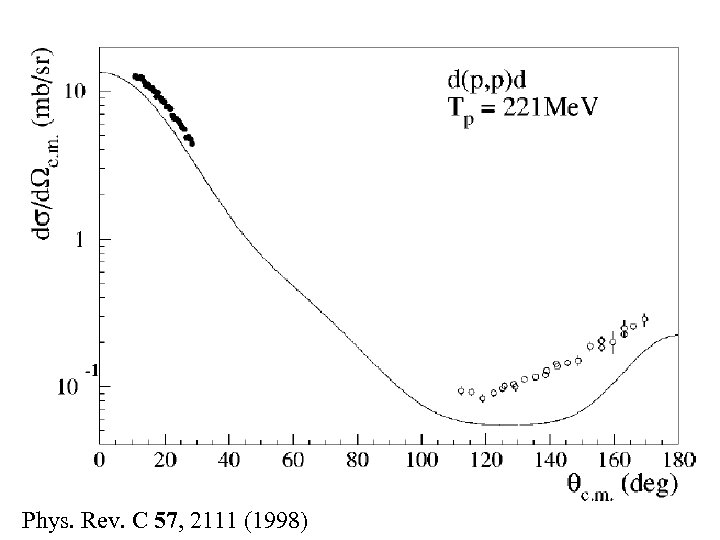
Phys. Rev. C 57, 2111 (1998)

相対論的修正 Faddeev方程式を相対論的に解く。 • ポテンシャルのローレンツ・ブースト • スピンのWigner回転 {
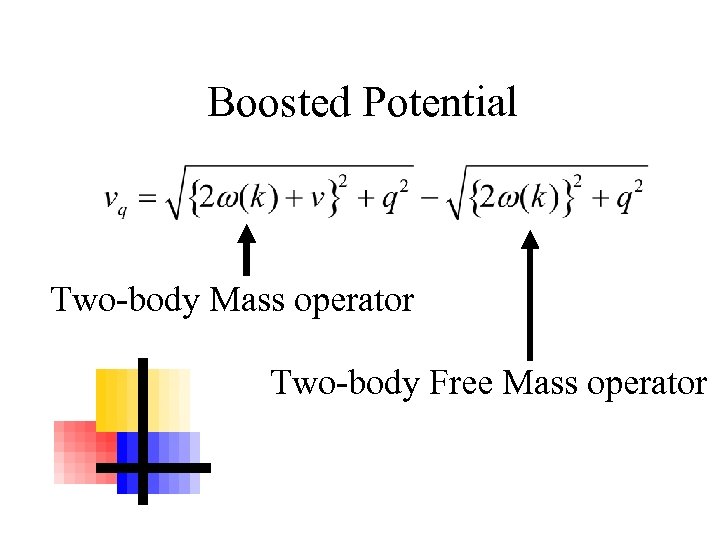
Boosted Potential Two-body Mass operator Two-body Free Mass operator

Boosted Potential OUTPUT 線形化して解く: INPUT Phys. Rev. C 66, 044010 (2002)

非線形のまま解く: Iteration Method Phys. Lett. B 655, 119(2007) nucl-th/0703010
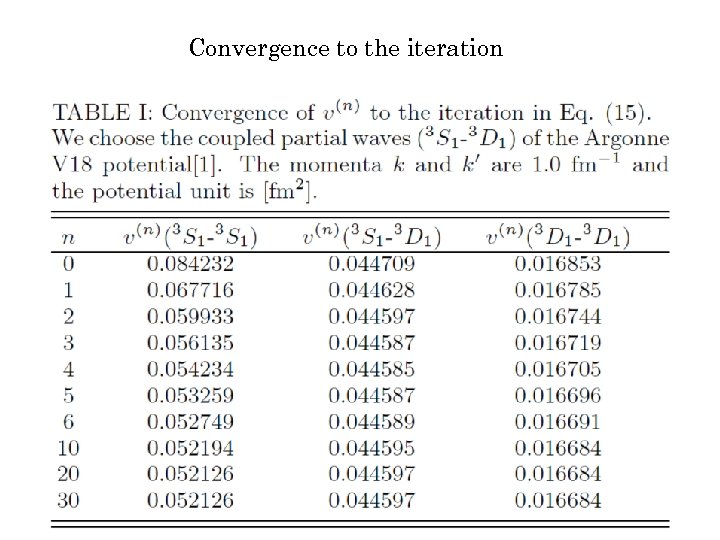
Convergence to the iteration
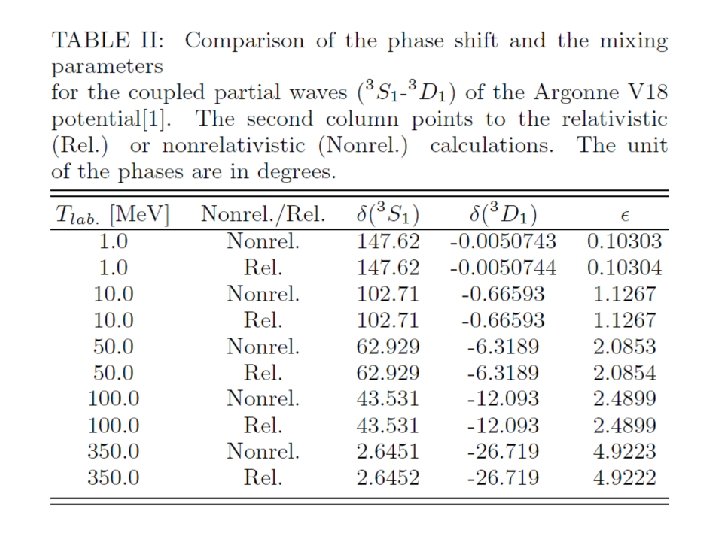
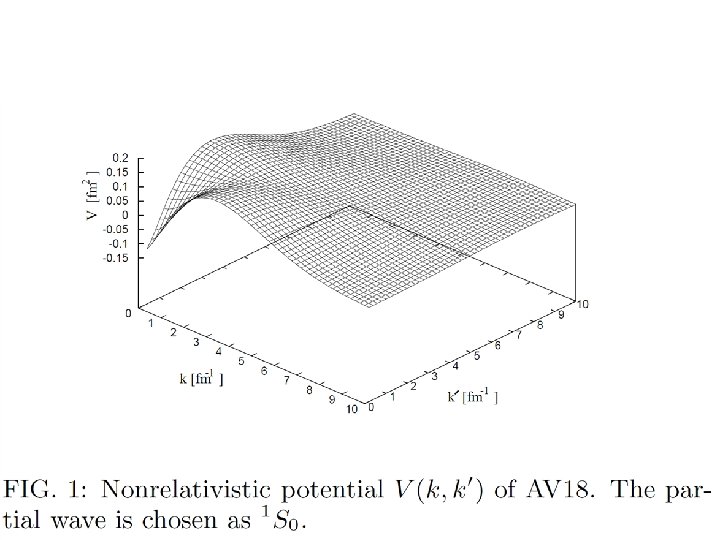
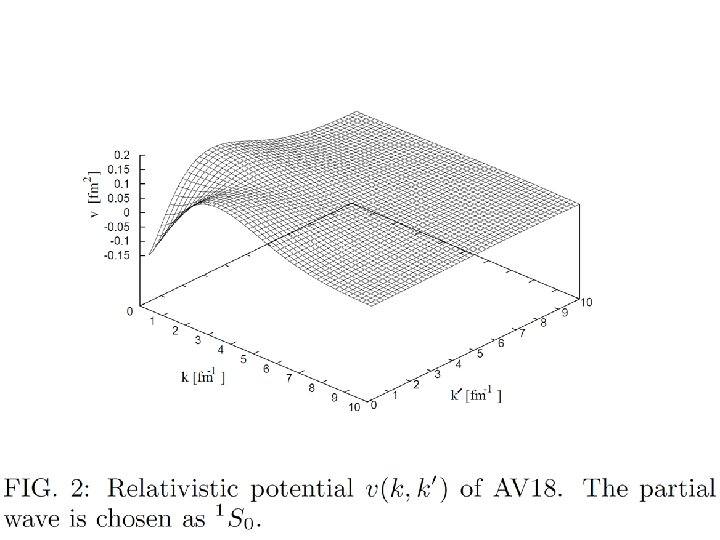

RESULTS: ★triton binding energy • Lorenz Boost • Wigner Rotation ★Scattering State ★Ay Puzzle
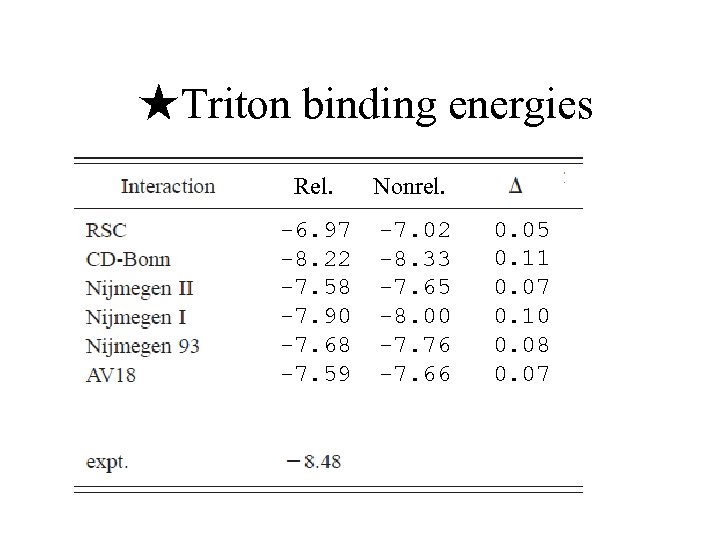
★Triton binding energies Rel. Nonrel. -6. 97 -8. 22 -7. 58 -7. 90 -7. 68 -7. 59 -7. 02 -8. 33 -7. 65 -8. 00 -7. 76 -7. 66 0. 05 0. 11 0. 07 0. 10 0. 08 0. 07

○Wigner Rotation
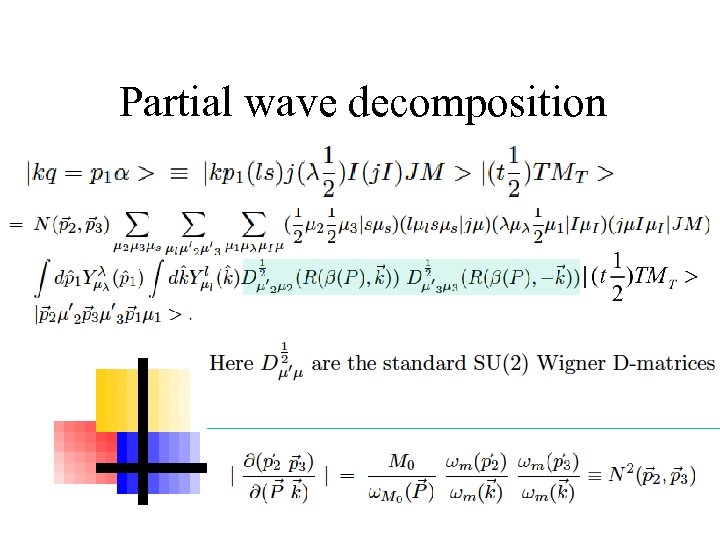
Partial wave decomposition
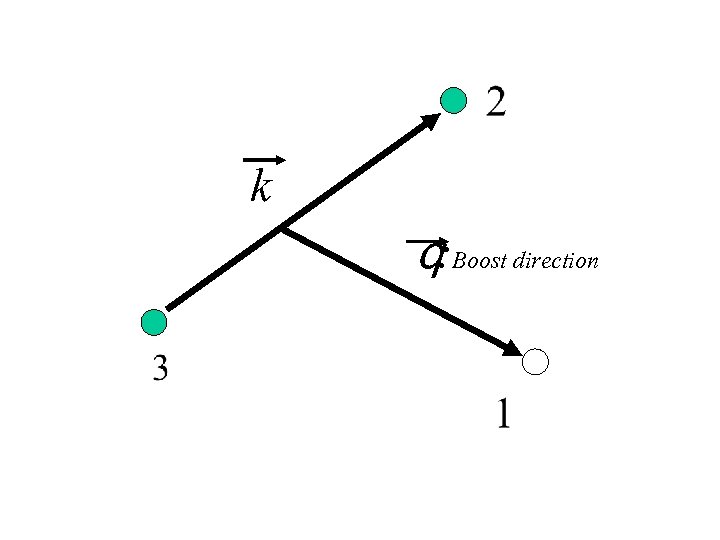
k qBoost direction :

Effect of Wigner Rotation 34ch Calculation with CD-Bonn (np) Nonrel. Relativistic (non-Wigner Rotation) Relativistic (Wigner Rotation) -8.247 -8.1459MeV -8.1443MeV Difference ~2keV

www. kyutech. ac. jp 相対論的効果(1) 100 ke. V程度、Tritonの結合エネル ギーは少なくなる。 ● Wigner回転の効果は、2 ke. V程度。 ●
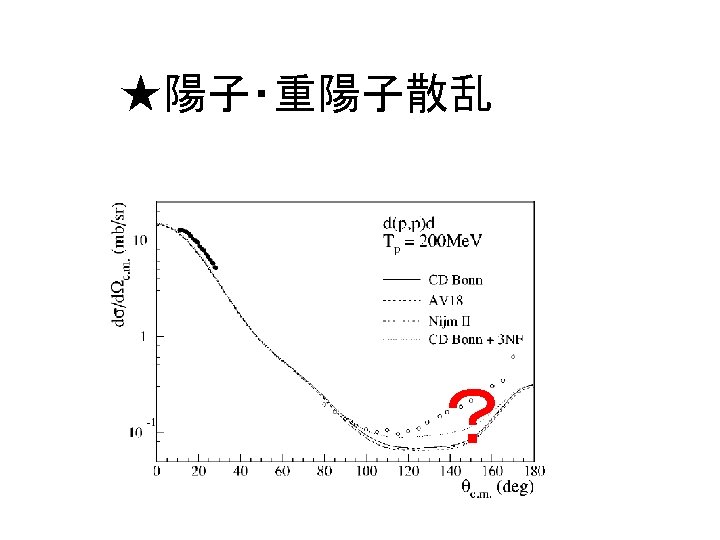
★陽子・重陽子散乱 ?
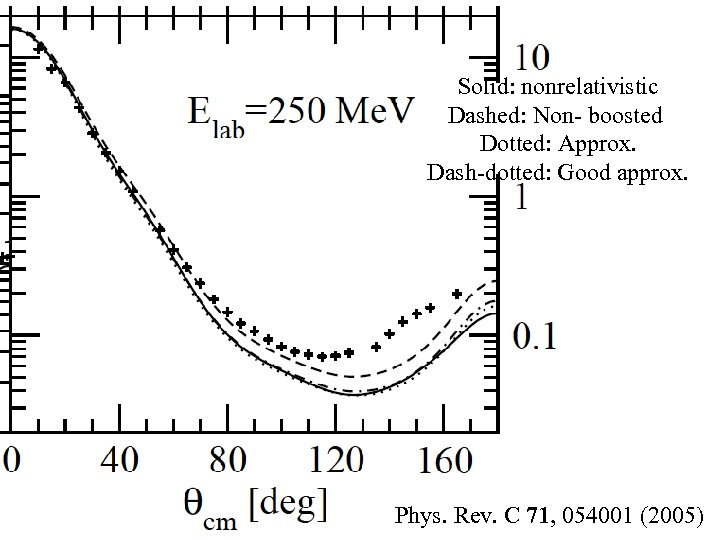
Solid: nonrelativistic Dashed: Non- boosted Dotted: Approx. Dash-dotted: Good approx. Phys. Rev. C 71, 054001 (2005)
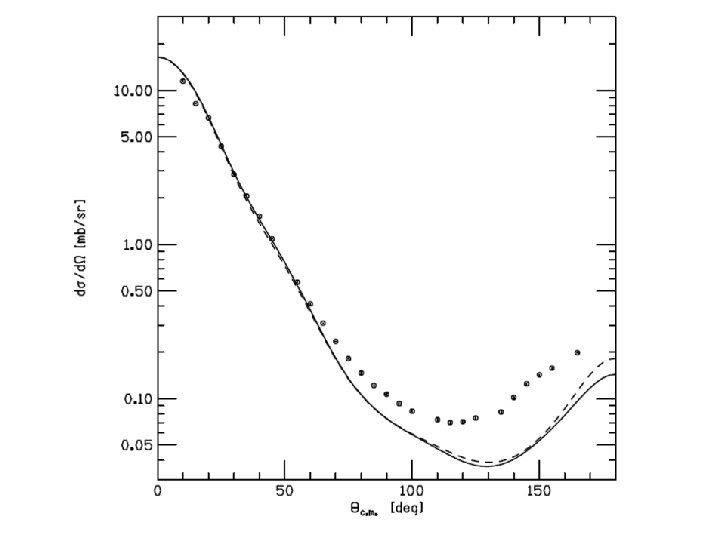
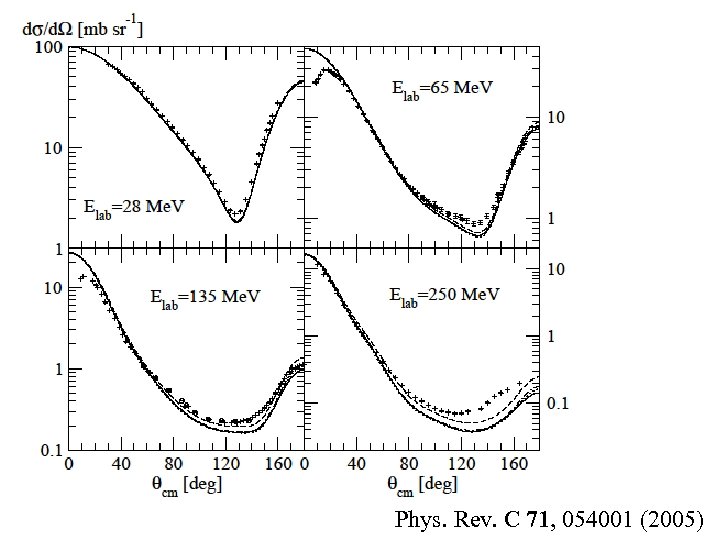
Phys. Rev. C 71, 054001 (2005)
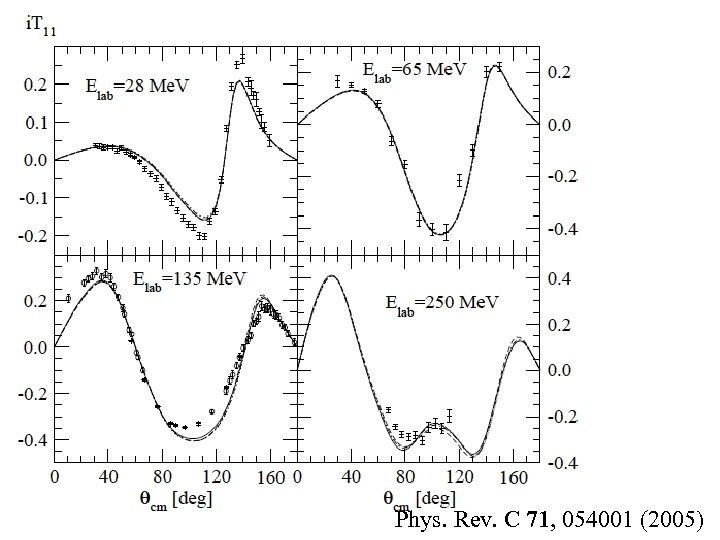
Phys. Rev. C 71, 054001 (2005)

www. kyutech. ac. jp 相対論的効果(2) 微分断面積の後方角度に小さな修正が出 来たが、解決に至らなかった。 高エネルギーで出現する新しい3体力の 可能性(πρ交換型、χEFT...)

Ayへの相対論的効果 • Physical Review C 77, 034004 (2008)
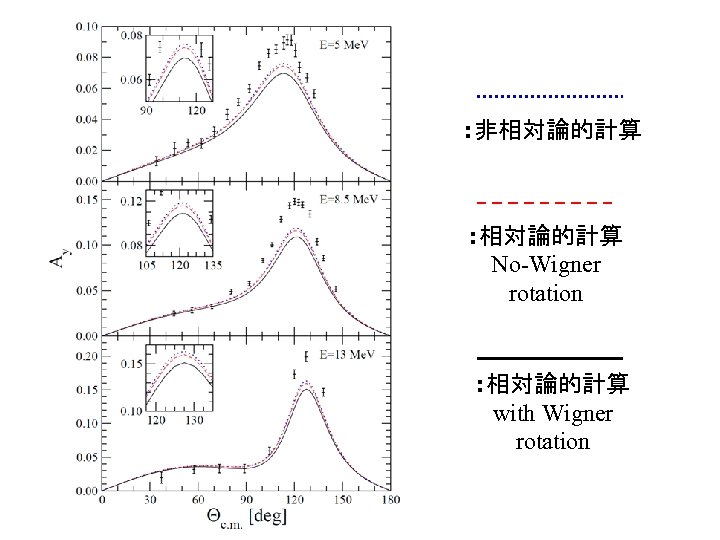
: 非相対論的計算 : 相対論的計算 No-Wigner rotation : 相対論的計算 with Wigner rotation
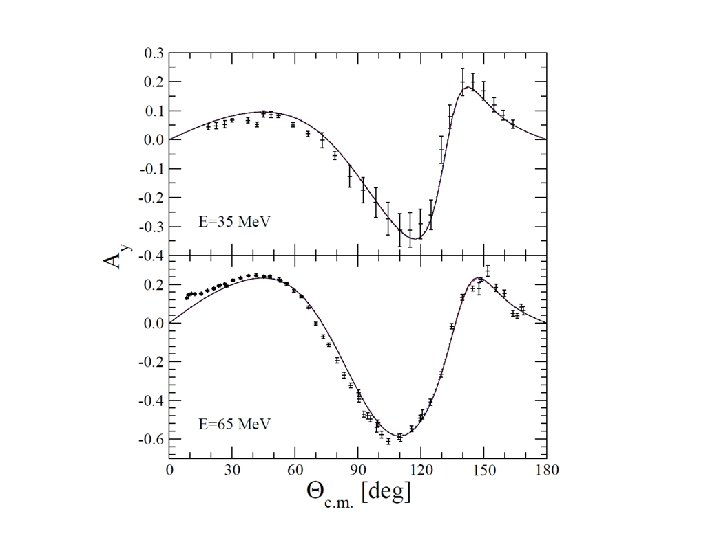

www. kyutech. ac. jp 相対論的効果(3) 実験値と理論値(非相対論)の違いに対 して、実験値と理論値(相対論)の違 いは、更に10%悪い方向に修正された。 ? 低エネルギーで出現する新しい3体力の 可能性(χEFT...)
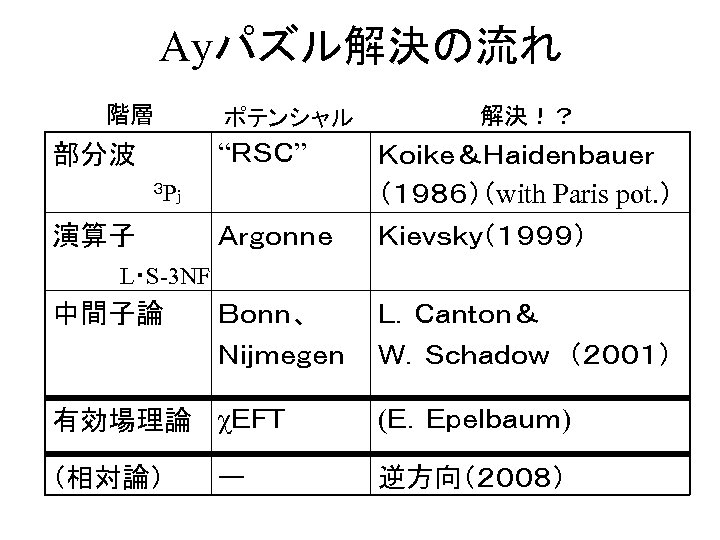
Ayパズル解決の流れ 階層 ポテンシャル 解決!? “RSC” 部分波 Koike&Haidenbauer (1986)(with Paris pot. ) Argonne Kievsky(1999) Bonn、 Nijmegen L.Canton& W.Schadow (2001) 3 Pj 演算子 L・S-3 NF 中間子論 有効場理論 χEFT (E.Epelbaum) (相対論) 逆方向(2008) ー

カイラル有効場理論の3体力 l LO→なし。 l NNLO→3つのタイプ。 藤田・宮沢type, E-type, D-type l NNNLO→色々。 但し、新しいパラメータは導入しなくても よい
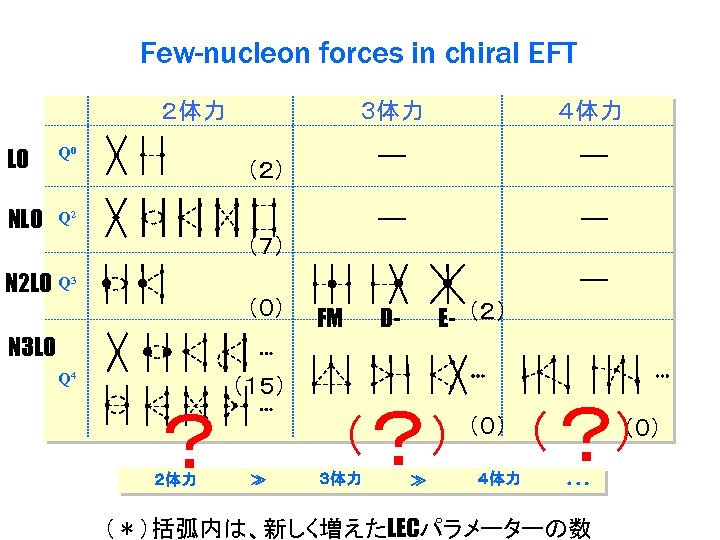
Few-nucleon forces in chiral EFT 2体力 LO Q 0 NLO 3体力 4体力 Q 2 (2) (7) N 2 LO Q 3 (0) N 3 LO Q 4 (15) ? 2体力 FM D- E- (2) ? ( ) 3体力 (0) 4体力 ? (0) ( ) (*)括弧内は、新しく増えたLECパラメーターの数
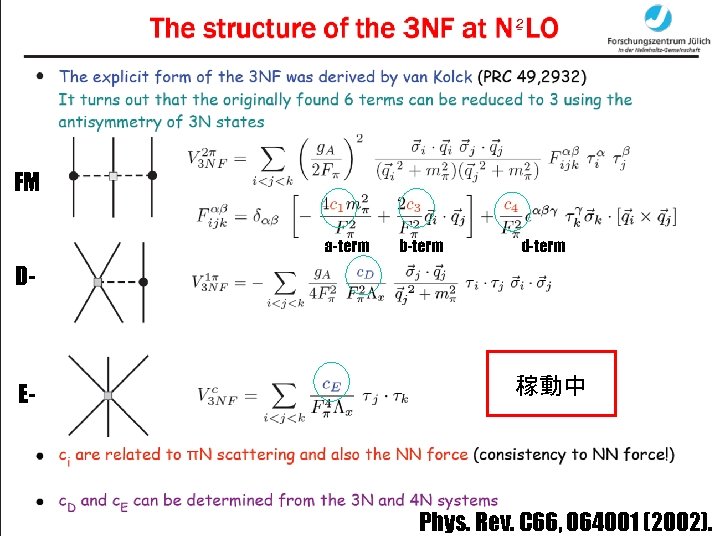
2 FM a-term b-term d-term D- E- 稼動中 Phys. Rev. C 66, 064001 (2002).
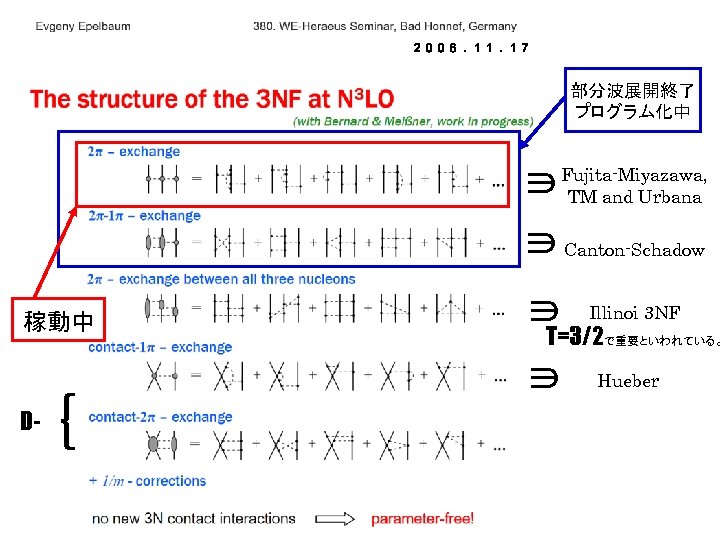
2006.11.17 部分波展開終了 プログラム化中 ∋ Fujita-Miyazawa, TM and Urbana ∋ Canton-Schadow 稼動中 D- { ∋ Illinoi 3 NF T=3/2で重要といわれている。 ∋ Hueber
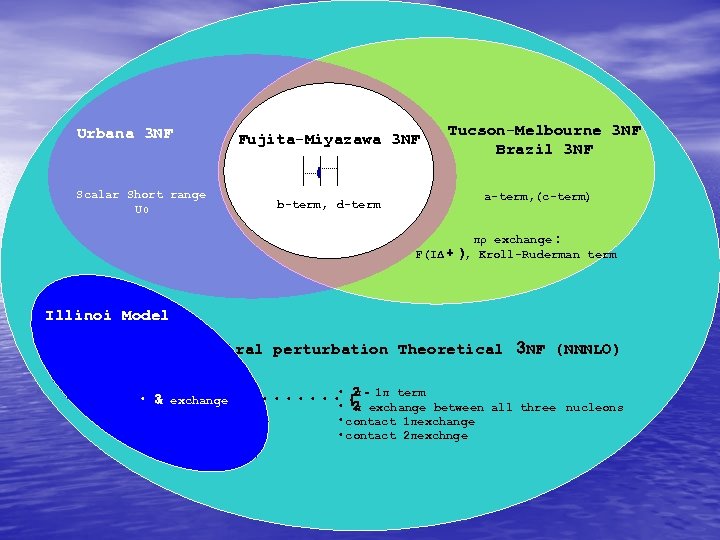
Urbana 3 NF Fujita-Miyazawa 3 NF Scalar Short range U 0 b-term, d-term Tucson-Melbourne 3 NF Brazil 3 NF a-term, (c-term) πρ exchange: F(IΔ+) Kroll-Ruderman term , Illinoi Model Chiral perturbation Theoretical 3 NF (NNNLO) ・3 exchange π ・2 1π term π- ・・・・・・・{ ・2 exchange between all three π nucleons ・ contact 1πexchange ・ contact 2πexchnge

NN, πNとリンクしている
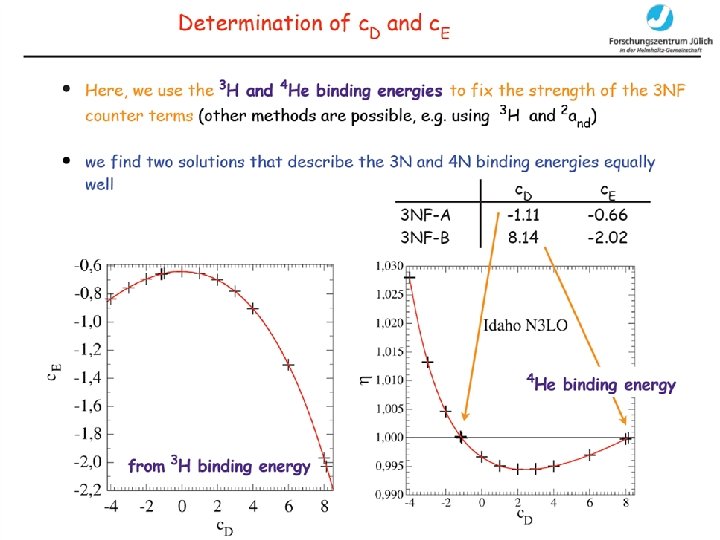

qについて、0次 1次 2次 1次 a-term∈NNLO b-term∈NNLO TM’ (c=0) c-term∈NNLO d-term∈NNLO c-term D-term アナログ a-term アナログ Few Body Syst. 30 (2001) 121
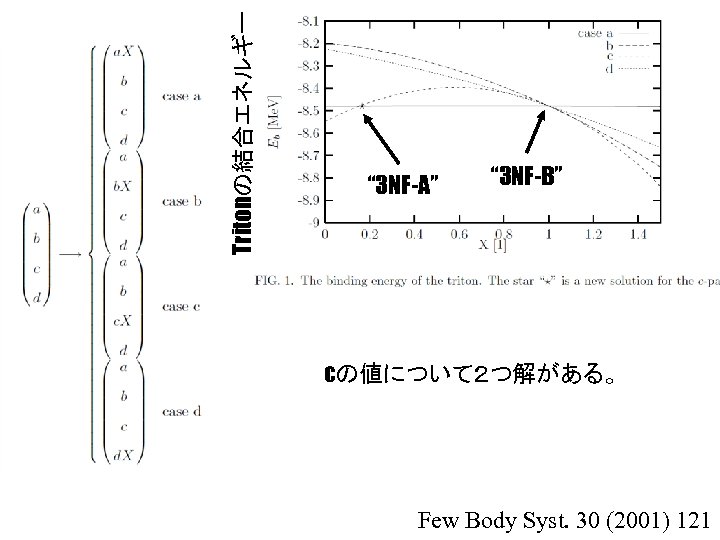
Tritonの結合エネルギー “ 3 NF-A” “ 3 NF-B” cの値について2つ解がある。 Few Body Syst. 30 (2001) 121

• N 3 LO(Idaho)+N 2 LO(FM+D-type+E-type) Triton, α粒子の結合エネルギーを与える解 が2つ。 “A”解、“B”解 。 Ep=250 Me. Vにおける陽子・重陽子散乱計算では、 どうなっているか?
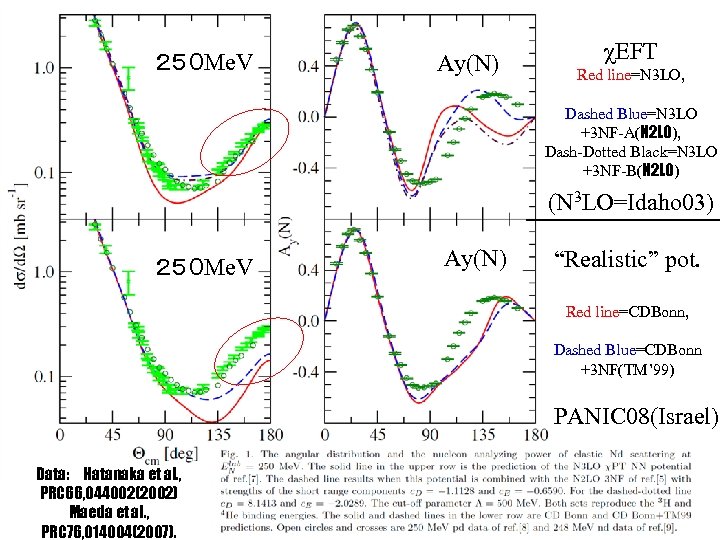
250 Me. V Ay(N) χEFT Red line=N 3 LO, Dashed Blue=N 3 LO +3 NF-A(N 2 LO), Dash-Dotted Black=N 3 LO +3 NF-B(N 2 LO) (N 3 LO=Idaho 03) 250 Me. V Ay(N) “Realistic” pot. Red line=CDBonn, Dashed Blue=CDBonn +3 NF(TM’ 99) PANIC 08(Israel) Data: Hatanaka et al. , PRC 66, 044002(2002) Maeda et al. , PRC 76, 014004(2007).
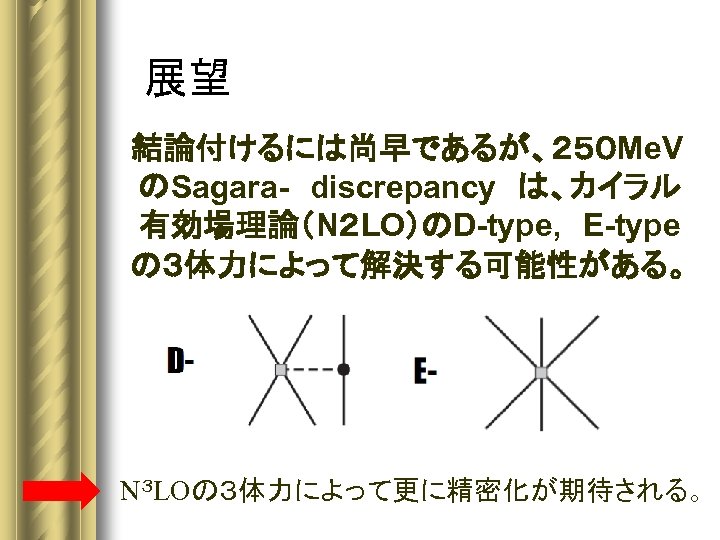
展望 結論付けるには尚早であるが、250 Me. V のSagara- discrepancy は、カイラル 有効場理論(N2 LO)のD-type, E-type の3体力によって解決する可能性がある。 N3 LOの3体力によって更に精密化が期待される。
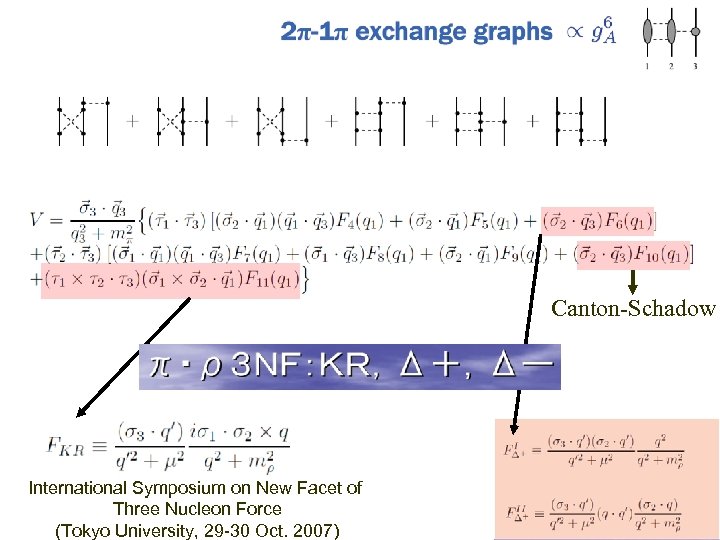
Canton-Schadow International Symposium on New Facet of Three Nucleon Force (Tokyo University, 29 -30 Oct. 2007)
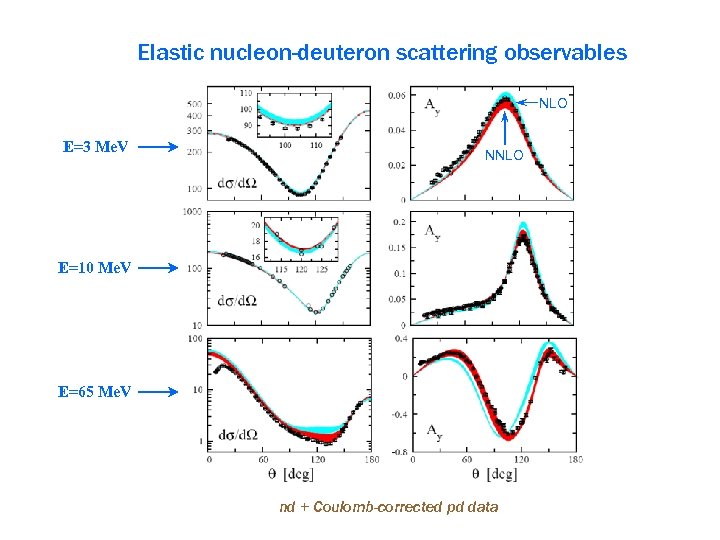
Elastic nucleon-deuteron scattering observables NLO E=3 Me. V NNLO E=10 Me. V E=65 Me. V nd + Coulomb-corrected pd data
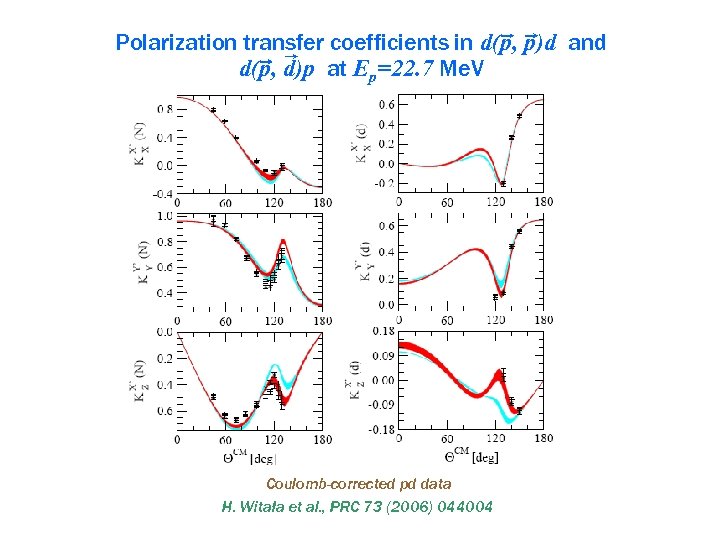
Polarization transfer coefficients in d(p, p)d and d(p, d)p at Ep=22. 7 Me. V Coulomb-corrected pd data H. Witała et al. , PRC 73 (2006) 044004
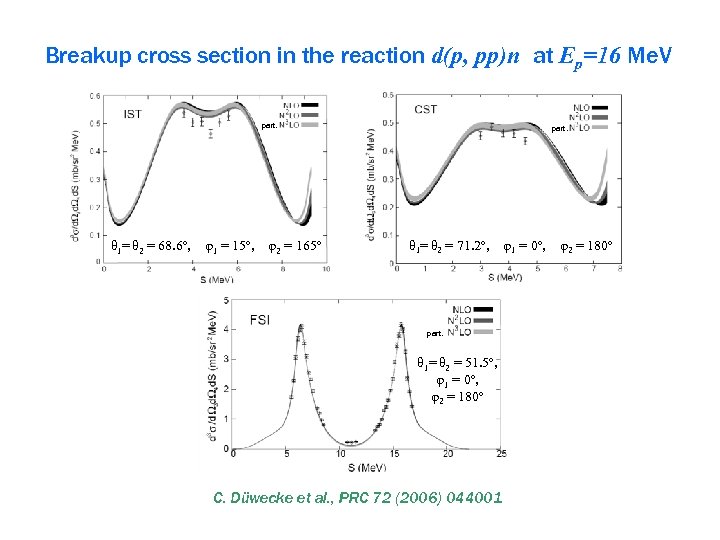
Breakup cross section in the reaction d(p, pp)n at Ep=16 Me. V part. θ 1= θ 2 = 68. 6º, φ1 = 15º, φ2 = 165º part. θ 1= θ 2 = 71. 2º, part. θ 1= θ 2 = 51. 5º, φ1 = 0º, φ2 = 180º C. Düwecke et al. , PRC 72 (2006) 044001 φ1 = 0º, φ2 = 180º
c77a447a1534478a7e99ca4a05bf764f.ppt