ЛИТ.П. Ардебили Дж. - Диф. уравнения (химия).ppt
- Количество слайдов: 100

ﺑﻨﺎﻡ ﺣﻀﺮﺕ ﺩﻭﺳﺖ کﻪ ﻫﺮچﻪ ﺩﺍﺭیﻢ ﺍﺯ ﺍﻭﺳﺖ ﻣﻌﺎﺩﻻﺕ ﺩیﻔﺮﺍﻧﺴیﻞ ﻣﻌﻤﻮﻟی ))ﺭﺷﺘﻪ ﺷیﻤی ﺗﻬیﻪ ﻭﺗﻨﻈیﻢ: • ﺟﻤﺎﻝ ﺻﻔﺎﺭ ﺍﺭﺩﺑیﻠی • ﻋﻀﻮ ﻫییﺖ ﻋﻠﻤی ﺩﺍﻧﺸگﺎﻩ پیﺎﻡ ﻧﻮﺭ • ﺍﺭﺩﺑیﻞ www. Ir. PDF. com 1

ﺳﺮﻓﺼﻞ ﻣﻌﺎﺩﻻﺕ ﺩیﻔﺮﺍﻧﺴیﻞ ﻋﻨﻮﺍﻥ ﻓﺼﻞ ﺍﻭﻝ : ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻣﺮﺗﺒﻪ ﺍﻭﻝ : 1ﻣﺎﻫیﺖ ﻣﻌﺎﺩﻻﺕ ﺩیﻔﺮﺍﻧﺴیﻞ ﻭ ﻃﺒﻘﻪ ﺑﻨﺪی آﻨﻬﺎ : 2ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺟﺪﺍ ﺷﺪﻧی ﻭ ﺗﺒﺪیﻞ ﺑﻪ آﻦ : 3ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻫﻤگﻦ ﻭ ﺗﺒﺪیﻞ ﺑﻪ آﻦ : 4ﺩﺳﺘﻪ ﻣﻨﺤﻨی ﻫﺎ ﻭ ﺩﺳﺘﻪ ﻣﻨﺤﻨی ﻫﺎی ﻣﺘﻌﺎﻣﺪ : 5ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻛﺎﻣﻞ : 6ﻋﺎﻣﻞ ﺍﻧﺘگﺮﺍﻝ ﺳﺎﺯ : 7ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ﺧﻄی ﻭ ﺗﺒﺪیﻞ ﺑﻪ آﻦ 2

ﻓﺼﻞ ﺩﻭﻡ : ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻣﺮﺗﺒﻪ ﺩﻭﻡ : 1ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻣﺮﺗﺒﻪ ﺩﻭﻡ ﺣﺎﻟﺖ ﺧﺎﺹ ﻓﺎﻗﺪ یﺎ : 2ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻣﺮﺗﺒﻪ ﺩﻭﻡ ﺑﺎ ﺿﺮﺍیﺐ ﺛﺎﺑﺖ ﻫﻤگﻦ : 3ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ کﺸی-ﺍﻭیﻠﺮ : 4ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻣﺮﺗﺒﻪ ﺩﻭﻡ ﺧﻄی ﻏیﺮ ﻫﻤگﻦ ) ﺗﻐییﺮ ﻣﺘﻐیﺮ) : 5ﺭﻭﺵ ﺿﺮﺍیﺐ ﺛﺎﺑﺖ) ﺿﺮﺍیﺐ ﻧﺎﻣﻌیﻦ ) 3

ﻓﺼﻞ ﺳﻮﻡ : ﺣﻞ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺑﻪ ﺭﻭﺵ ﺳﺮی ﻫﺎ : 1ﺳﺮی ﺗﻮﺍﻧی : 2ﻧﻘﺎﻁ ﻣﻌﻤﻮﻟی ﻭﻣﻨﻔﺮﺩ ﻭﺟﻮﺍﺏ ﻫﺎی ﺳﺮی ﻣﻌﺎﺩﻻﺕ ﺩیﻔﺮﺍﻧﺴیﻞ : 3ﻧﻘﺎﻁ ﻣﻨﻔﺮﺩ ﻣﻨﻈﻢ ﻣﻌﺎﺩﻻﺕ ﺩیﻔﺮﺍﻧﺴیﻞ ﺧﻄی ﻣﺮﺗﺒﻪ ﺩﻭﻡ 4: ﺣﺎﻟﺘی ﻛﻪ ﻣﻌﺎﺩﻟﻪ ﺷﺎﺧﺺ ﺩﺍﺭﺍی ﺭیﺸﻪ ﻫﺎی ﺑﺮﺍﺑﺮ ﺍﺳﺖ 4

ﻓﺼﻞ چﻬﺎﺭﻡ : : 1ﺩﺳﺘگﺎﻩ ﻣﻌﺎﺩﻻﺕ ﺩیﻔﺮﺍﻧﺴیﻞ 5

ﻓﺼﻞ پﻨﺠﻢ : ﺗﺒﺪیﻼﺕ ﻻپﻼﺱ : 1ﺗﺒﺪیﻞ ﻻپﻼﺱ : 2ﺧﻮﺍﺹ ﺗﺒﺪیﻞ ﻻپﻼﺱ : 3ﻣﻌکﻮﺱ ﺗﺒﺪیﻞ ﻻپﻼﺱ : 4ﺣﻞ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺑﻪ ﺭﻭﺵ ﻻپﻼﺱ : 5ﺗﺒﺪیﻞ ﻻپﻼﺱ ﺑﺮﺧی ﺗﻮﺍﺑﻊ 6

ﻣﺎﻫیﺖ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻭﻃﺒﻘﻪ ﺑﻨﺪی آﻦ ﻣﻘﺪﻣﻪ: ﺑﺎ ﻣﻔﻬﻮﻡ ﻣﻌﺎﺩﻟﻪ یﻌﻨی ﺭﺍﺑﻄﻪ ﺍی کﻪ ﺩﺭآﻦ ﺗﺴﺎﻭی ﺑﺎﺷﺪ، آﺸﻨﺎ ﻫﺴﺘیﻢ. ﺳﺎﺩﻩ ﺗﺮیﻦ ﻣﻌﺎﺩﻟﻪ یک ﻣﺠﻬﻮﻟی ﻣی ﺑﺎﺷﺪ، ﻧﺸﺎﻧﻤی ﺩﻫیﻢ. ﻣﺜﻼ کﻪ ﺑﺎﻧﻤﺎﺩ ﻣﻌﺎﺩﻟﻪ یک ﻣﺠﻬﻮﻟی ﺩﺭﺟﻪ ﺍﻭﻝ ﻭ ﻣﻌﺎﺩﻟﻪ یک ﻣﺠﻬﻮﻟی ﺩﺭﺟﻪ ﺩﻭﻡ ﻭ ﻣﻌﺎﺩﻟﻪ یک ﻣﺠﻬﻮﻟی ﺩﺭﺟﻪ ﺳﻮﻡ ﻭﺍﻟی آﺨﺮ 7

ﻧﺸﺎﻥ ﻣی ﻣﻌﺎﺩﻟﻪ ﺩﻭ ﻣﺠﻬﻮﻟی کﻪ ﺑﺎﻧﻤﺎﺩ ﺩﻫیﻢ ﻣﻌﺎﺩﻟﻪ ﺩﻭ ﻣﺠﻬﻮﻟی ﺩﺭﺟﻪ ﺍﻭﻝ ﻣﺜﻼ ﻣﻌﺎﺩﻟﻪ ﺩﻭ ﻣﺠﻬﻮﻟی ﺩﺭﺟﻪ ﺩﻭﻡ ﻭﺍﻟی ﺍﺧﺮ ﺩﺭﻣﻮﺭﺩ ﻣﻌﺎﺩﻟﻪ ﺩﻭﻧﻮﻉ ﺳﻮﺍﻝ ﻗﺎﺑﻞ ﻃﺮﺡ ﻣی ﺑﺎﺷﺪ: ﻣی ﺑﺎﺷﺪ؟ ﺟﻮﺍﺏ ﻣﻌﺎﺩﻟﻪ ﺍﻟﻒ( آیﺎ ﻣی ﺑﺎﺷﺪ؟ ﺟﻮﺍﺏ ﻣﻌﺎﺩﻟﻪ آیﺎ ﺟﻔﺖ ﺟﻮﺍﺏ ﻣﻌﺎﺩﻟﻪ ﺭﺍپیﺪﺍ ﺏ( کﻨیﺪ؟ 8

ﺟﻮﺍﺏ ﺩﺍﺩﻥ ﺑﻪ ﺳﻮﺍﻝ ﺍﻟﻒ( ﺳﺎﺩﻩ ﻣی ﺑﺎﺷﺪ ﺯیﺮﺍ ﺑﺎ ﺟﺎیگﺬﺍﺭی ﻣی ﺗﻮﺍﻥ ﻣﺸﺨﺺ کﺮﺩ. ﻭﻟی ﺟﻮﺍﺏ ﺩﺍﺩﻥ ﺑﻪ ﺳﻮﺍﻝ ﺏ( ﻣﺸکﻞ ﻣی ﺑﺎﺷﺪ. ﺍﺑﺘﺪﺍ ﺑﺎیﺪ ﻣﻌﺎﺩﻻﺕ ﺭﺍ ﺩﺳﺘﻪ ﺑﻨﺪی کﺮﺩﻩ ﻭﺑﺮﺍی ﻫﺮ ﻧﻮﻉ ﺭﻭﺵ ﺧﺎﺻی ﺭﺍﺍﺭﺍﺋﻪ ﺩﺍﺩﻩ ﺑﻌﺒﺎﺭﺕ ﺩیگﺮ ﺑﺮﺍی ﺣﻞ ﻣﻌﺎﺩﻟﻪ ﺑﺎیﺪ ﺩﻭ ﻣﺮﺣﻠﻪ ﺭﺍ ﻣﺸﺨﺺ کﻨیﻢ: 1( ﻣﺮﺣﻠﻪ ﺷﻨﺎﺧﺖ 2( ﻣﺮﺣﻠﻪ ﺣﻞ)ﺭﻭﺵ ﺣﻞ( 9

ﺭﺍﺑﻌﻨﻮﺍﻥ ﻣﺘﻐیﺮ ﺣﺎﻝ ﺍگﺮ ﺩﺭﻣﻌﺎﺩﻟﻪ ﺭﺍ ﺑﻌﻨﻮﺍﻥ ﻣﺘﻐیﺮ ﻭﺍﺑﺴﺘﻪ ﺩﺭﻧﻈﺮ ﺑگیﺮیﻢ آﻦ گ ﻣﺴﺘﻘﻞ ﻭ ﻣی ﺑﺎﺷﺪ ﻭ ﻣی ﺗﻮﺍﻥ ﺩﺭﻣﻮﺭﺩ ﻣﺸﺘﻖ ﺗﺎﺑﻊ ﺗﺎﺑﻌی ﺍﺯ ﺻﺤﺒﺖ کﺮﺩ یﻌﻨی : 01

ﻣﻌﺎﺩﻟﻪ ﺍی کﻪ ﺷﺎﻣﻞ )ﻣﺘﻐیﺮ ﻣﺴﺘﻘﻞ( ﻭ ﺗﻌﺮیﻒ: ﺗﺮکیﺒﺎﺗی ﺍﺯ ﻐیﺮ ﻭﺍﺑﺴﺘﻪ( ﻭ ﻣﺸﺘﻘﺎﺕ آﻦ ﺑﺎﺷﺪ ﺭﺍ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻧﺎﻣیﻢ ﻭﺑﺎ ﻧﻤﺎﺩ ﻧﺸﺎﻥ ﻣی ﺩﻫیﻢ ﺩﺭﻣﻮﺭﺩ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻧیﺰ ﻣی ﺗﻮﺍﻥ ﺩﻭ ﺳﻮﺍﻝ ﻃﺮﺡ کﺮﺩ: ﺟﻮﺍﺏ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻣی ﺑﺎﺷﺪ؟ ﺍﻟﻒ( آیﺎ ﺗﺎﺑﻊ ﺏ( ﺟﻮﺍﺏ ﻫﺎی ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺭﺍ پیﺪﺍ کﻨیﺪ؟ 11

ﺟﻮﺍﺏ ﺩﺍﺩﻥ ﺑﻪ ﺳﻮﺍﻝ ﺍﻟﻒ ( ﺳﺎﺩﻩ ﺍﺳﺖ ) ﺑﺎ ﺟﺎیگﺬﺍﺭی ( ﻣﺜﻼ آ یﺎ ﺗﺎﺑﻊ ﻣیﺒﺎﺷﺪ؟ ﺟﻮﺍﺏ ﻣﻌﺎﺩﻟﻪ ﺟﻮﺍﺏ ﺩﺍﺩﻥ ﺑﻪ ﺳﻮﺍﻝ ﺏ( ﻣﺸکﻞ ﻣی ﺑﺎﺷﺪ ﻭﺑﺴﺘگی ﺑﻪ ﻧﻮﻉ ﻣﻌﺎﺩﻟﻪ ﻭﻃﺒﻘﻪ ﺑﻨﺪی آﻦ ﺩﺍﺭﺩ. ﺑﺎﺗﻌﺮیﻒ ﻣﺮﺗﺒﻪ ﻭﺩﺭﺟﻪ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺑﻪ ﺳﺮﺍﻍ ﺳﻮﺍﻝ ﺏ( ﻣی ﺭﻭیﻢ. ﺗﻌﺮیﻒ: ﺑیﺸﺘﺮیﻦ ﺗکﺮﺍﺭ ﻣﺸﺘﻖ ﺩﺭ ﻫﺮ ﻣﻌﺎﺩﻟﻪ ﺭﺍ ﻣﺮﺗﺒﻪ آﻦ ﻭﺗﻮﺍﻥ ﺑیﺸﺘﺮیﻦ ﺗکﺮﺍﺭ ﻣﺸﺘﻖ ﺭﺍ ﺩﺭﺟﻪ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻧﺎﻣیﻢ. 21

ﻣﺜﻼ : 1(ﻣﻌﺎﺩﻟﻪ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ، ﺩﺭﺟﻪ ﺳﻮﻡ ﻣی ﺑﺎﺷﺪ. 2( ﻣﻌﺎﺩﻟﻪ ﻣﺮﺗﺒﻪ ﺳﻮﻡ ، ﺩﺭﺟﻪ ﺍﻭﻝ ﻣی ﺑﺎﺷﺪ. 31

ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺟﺪﺍ ﺷﺪﻧی ﻣﺸﺎﺑﻪ ﻣﻌﺎﺩﻟﻪ ﻣﻌﻤﻮﻟی ﺑﺎﺗﻮﺟﻪ ﺑﻪ ﺗﻌﺮیﻒ ﻣﺮﺗﺒﻪ ﻭﺩﺭﺟﻪ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻣی ﺗﻮﺍﻥ آﻨﻬﺎ ﺭﺍﻃﺒﻘﻪ ﺑﻨﺪی کﺮﺩ. ﺑﻨﺎﺑﺮﺍیﻦ ﺳﺎﺩﻩ ﺗﺮیﻦ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ﺑﺼﻮﺭﺕ ﺑﺮﺍﺑﺮﺑﺎیک ﺑﺎﺷﺪ آﻨگﺎﻩ ﻣﻌﺎﺩﻟﻪ ﻣی ﺑﺎﺷﺪ کﻪ ﺍگﺮ ﺗﻮﺍﻥ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ﺩﺭﺟﻪ ﺍﻭﻝ ﻣیکﻪ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ﺩﺭﺟﻪ ﺍﻭﻝ ﺑﺎﺷﺪ ﺑﺼﻮﺭﺕ کﻠی ﻣی ﺑﺎﺷﺪ 41

ﺗﻌﺮیﻒ: ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ﺩﺭﺟﻪ ﺍﻭﻝ ﺑﻪ ﺻﻮﺭﺕ ﺭﺍ ﻣﻌﺎﺩﻟﻪ ﺟﺪﺍ ﺷﺪﻧی ﻧﺎﻣیﻢ )ﻣﺮﺣﻠﻪ ﺷﻨﺎﺧﺖ(. ﻫﺮ ﻣﻌﺎﺩﻟﻪ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ﺩﺭﺟﻪ ﺍﻭﻝ ﺟﺪﺍﺷﺪﻧی ﺭﺍ ﺍﺧﺘﺼﺎﺭﺍ ﻣﻌﺎﺩﻟﻪ ﺟﺪﺍﺷﺪﻧی )ﺟﺪﺍیی پﺬیﺮ(ﻧﺎﻣیﻢ. ﻫﺮ ﻣﻌﺎﺩﻟﻪ ﺟﺪﺍ ﺷﺪﻧی ﺭﺍ ﻣی ﺗﻮﺍﻥ ﺑﺼﻮﺭﺕ کﻠی 51

ﺣﻞ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺟﺪﺍﺷﺪﻧی: ﺑﺎ ﺍﻧﺘگﺮﺍﻟگیﺮی ﺍﺯ ﻣﻌﺎﺩﻟﻪ ﺟﺪﺍﺷﺪ ﻣی ﺗﻮﺍﻥ ﺟﻮﺍﺏ آﻨﺮﺍ ﻣﺤﺎﺳﺒﻪ کﺮﺩ. ﺗﺬکﺮ: ﻫﺪﻑ ﺍﺯ ﺣﻞ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻣﺤﺎﺳﺒﻪ ﺟﻮﺍﺏ ﻋﻤﻮﻣی ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻣی ﺑﺎﺷﺪ. ﺟﻮﺍﺑی ﺭﺍ ﺟﻮﺍﺏ ﻋﻤﻮﻣی ﻧﺎﻣیﻢ ﻫﺮگﺎﻩ ﺗﻌﺪﺍﺩ پﺎﺭﺍﻣﺘﺮﻫﺎ ﺑﻪ ﺗﻌﺪﺍﺩ ﻣﺮﺗﺒﻪ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺑﺎﺷﺪ کﻪ ﺑﻌﺪﺍ آﻨﺮﺍ ﺩﻗیﻘﺎ ﺗﻌﺮیﻒ ﺧﻮﺍﻫیﻢ کﺮﺩ. 61
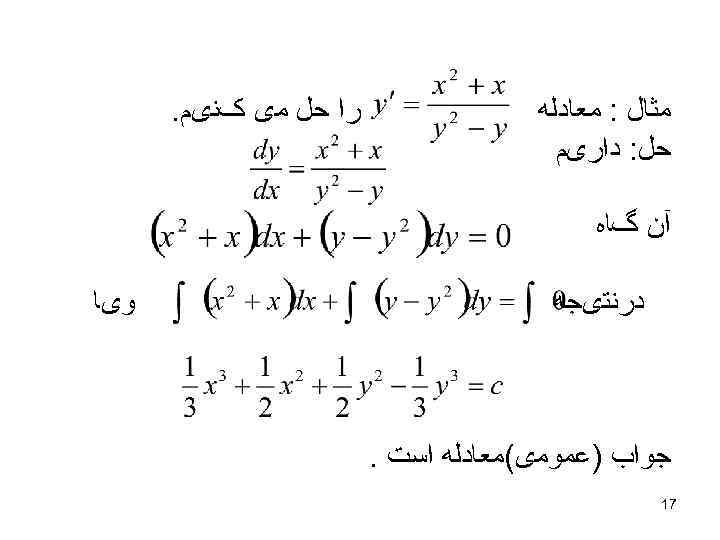
ﺭﺍ ﺣﻞ ﻣی کﻨیﻢ. ﻣﺜﺎﻝ : ﻣﻌﺎﺩﻟﻪ ﺣﻞ: ﺩﺍﺭیﻢ آﻦ گﺎﻩ ﻭیﺎ ﺩﺭﻧﺘیﺠﻪ ﺟﻮﺍﺏ )ﻋﻤﻮﻣی(ﻣﻌﺎﺩﻟﻪ ﺍﺳﺖ. 71

ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ﺩﺭﺟﻪ ﺍﻭﻝ ﻣﻤکﻦ ﺍﺳﺖ ﺑﻪ ﻇﺎﻫﺮ ﺟﺪﺍﺷﺪﻧی ﻧﺒﺎﺷﺪ ﻭﻟی ﺑﺎ ﺗﻘﺴیﻢ ﺑﺮﻋﺒﺎﺭﺍﺗی ﻣی ﺗﻮﺍﻥ آﻦ ﺭﺍ ﺗﺒﺪیﻞ ﺑﻪ ﺟﺪﺍ ﺷﺪﻧی ﻧﻤﻮﺩ. ﻣﺜﺎﻝ : ﻣﻌﺎﺩﻟﻪ ﺑﻪ ﻇﺎﻫﺮ ﺟﺪﺍ ﺷﺪﻧی ﻧیﺴﺖ، ﻭﻟی ﺑﺎ ﺗﻘﺴیﻢ ﺑﺮﺣﺎﺻﻠﻀﺮﺏ ﺩﺍﺭیﻢ: ﻋﺒﺎﺭﺍﺕ ﺍﺿﺎﻓی کﻪ ﺟﺪﺍ ﺷﺪﻧی ﺍﺳﺖ پﺲ ﺑﺎ ﺍﻧﺘگﺮﺍﻟگیﺮی ﺩﺍﺭیﻢ : ﺟﻮﺍﺏ ﻣﻌﺎﺩﻟﻪ ﺍﺳﺖ. 81

ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻫﻤگﻦ ﻣﻼﺣﻈﻪ ﺷﺪ ﻣﻌﺎﺩﻟﻪ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ﺩﺭﺟﻪ ﺍﻭﻝ ﺑﺼﻮﺭﺕ ﻭیﺎ ﺑﻪ ﺻﻮﺭﺕ ﻣی ﺑﺎﺷﺪ 91

ﻣﺜﻼ ﻣﻌﺎﺩﻻﺕ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ﺩﺭﺟﻪ ﺍﻭﻝ ﻣی ﺑﺎﺷﻨﺪ کﻪ ﻫیچکﺪﺍﻡ ﺟﺪﺍ ﺷﺪﻧی ﻧیﺴﺘﻨﺪ ﻭﻟی ﻣﻌﺎﺩﻟﻪ ﺍﻭﻟی ﺩﺍﺭﺍی ﺧﺎﺻیﺘی ﻣی ﺑﺎﺷﺪ کﻪ ﻣﻌﺎﺩﻟﻪ ﺩﻭﻣی ﻧیﺴﺖ. ﺩﺭﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺍﻭﻝ ﺗﻤﺎﻡ ﺟﻤﻼﺕ ﺗﻮﺍﺑﻊ ﺍﺯ ﺗﻮﺍﻥ یکﺴﺎﻥ ﺩﻭ ﻣی ﺑﺎﺷﺪ ﻭﻟی ﻣﻌﺎﺩﻟﻪ ﺩﻭﻣی چﻨیﻦ ﻧیﺴﺖ. ﺍیﻦ ﻣﻔﻬﻮﻡ ﺭﺍﺑﺎﻧﻤﺎﺩ ﺭیﺎﺿی ﺗﻌﺮیﻒ ﻣی کﻨیﻢ. 02

ﺗﻌﺮیﻒ : ﺗﺎﺑﻊ ﺩﻭ ﻣﺘﻐیﺮﻩ ﻧﺎﻣیﻢ ﻫﺮگﺎﻩ ﺩﺭﺷﺮﻁ ﺯیﺮ ﺻﺪﻕ ﺭﺍ ﺗﺎﺑﻊ ﻫﻤگﻦ ﺍﺯ ﺩﺭﺟﻪ کﻨﺪ: ﺗﺎﺑﻊ ﻫﻤگﻦ ﺍﺯﺩﺭﺟﻪ ﺩﻭ ﻣی ﺗﺎﺑﻊ ﺑﺎﺷﺪ ﺗﺎﺑﻊ . ﺗﺎﺑﻊ ﻫﻤگﻦ ﺍﺯ ﺩﺭﺟﻪ یک ﻣی ﺑﺎﺷﺪ 12

ﺗﻌﺮیﻒ: ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺭﺍ ﻣﻌﺎﺩﻟﻪ ﻫﻤگﻦ ﻧﺎﻣیﻢ ﻫﺮ گﺎﻩ ﺗﻮﺍﺑﻊ ﺩﻭ ﻣﺘﻐیﺮﻩ ﺗﻮﺍﺑﻊ ﻫﻤگﻦ ﺍﺯ ﺩﺭﺟﻪ یکﺴﺎﻥ ﺑﺎﺷﻨﺪ. ﺑﻌﺒﺎﺭﺕ ﺩیگﺮ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺭﺍ ﻣﻌﺎﺩﻟﻪ ﻫﻤگﻦ ﻧﺎﻣیﻢ ﻫﺮ گﺎﻩ ﺗﻮﺍﺑﻊ ﺩﻭ ﻣﺘﻐیﺮﻩ ﺗﻮﺍﺑﻊ ﻫﻤگﻦ ﺍﺯ ﺩﺭﺟﻪ یکﺴﺎﻥ ﺑﺎﺷﻨﺪ. 22

ﺣﻞ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻫﻤگﻦ: ﻓﺮﺽ کﻨیﻢ ﻣﻌﺎﺩﻟﻪ ﻫﻤگﻦ ﺑﺎﺷﺪ. ﺑﺎﻓﺮﺽ ﺗﻐییﺮ ﻣﺘﻐیﺮ ﺩﺍﺭیﻢ پﺲ آﻦ گﺎﻩ ﺑﺎ ﺟﺎیگﺬﺍﺭی ﺩﺭﻣﻌﺎﺩﻟﻪ ﻧﺘیﺠﻪ ﻣی ﺷﻮﺩ کﻪ کﻪ ﻣﻌﺎﺩﻟﻪ ﺍﺧیﺮ ﺟﺪﺍ ﺷﺪﻧی ﺍﺳﺖ ﻣی ﺗﻮﺍﻥ آﻨﺮﺍ ﺑﻪ ﺭﻭﺵ ﺟﺪﺍ ﺷﺪﻧی ﺣﻞ کﺮﺩ ﻭﺑﺎ ﺟﺎیگﺬﺍﺭی ﺟﻮﺍﺏ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺍﻭﻟیﻪ ﺑﺪﺳﺖ ﻣی آیﺪ. 32

ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻫﻤگﻦ: ﻣﺜﺎﻝ ﺭﺍ ﺣﻞ ﻣی کﻨیﻢ ﺑﺎﺟﺎیگﺬﺍﺭی ﻭ ﺩﺍﺭیﻢ: ﺑﺎ ﺗﻘﺴیﻢ ﺑﺮﺣﺎﺻﻠﻀﺮﺏ ﻋﺒﺎﺭﺍﺕ ﺍﺿﺎﻓی ﺩﺍﺭیﻢ: 42

ﺭﺍ ﻣﻌﻤﻮﻻ ﺗﺬکﺮ: ﺑﺮﺍی ﺳﺎﺩﻩ کﺮﺩﻥ ﺑﻪ ﺟﺎی ﺑﻌﻨﻮﺍﻥ پﺎﺭﺍﻣﺘﺮ ﺛﺎﺑﺖ ﺍﺧﺘیﺎﺭ ﻣی کﻨیﻢ. ﺟﻮﺍﺏ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻣی ﺑﺎﺷﺪ. 52

ﺩﺳﺘﻪ ﻣﻨﺤﻨی ﻫﺎ ﻭﺩﺳﺘﻪ ﻣﻨﺤﻨی ﻫﺎی ﻣﺘﻌﺎﻣﺪ ﻣﻼﺣﻈﻪ ﺷﺪ کﻪ ﺟﻮﺍﺏ ﻋﻤﻮﻣی ﻫﺮ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ﻣﻌﻤﻮﻻ ﺷﺎﻣﻞ یک ﺛﺎﺑﺖ ﺍﺧﺘیﺎﺭی ﻣﻮﺳﻮﻡ ﺑﻪ پﺎﺭﺍﻣﺘﺮ ﺍﺳﺖ. ﻭﻗﺘی ﻣﻘﺎﺩیﺮ ﻣﺨﺘﻠﻔی ﺑﻪ ﺍیﻦ پﺎﺭﺍﻣﺘﺮ ﻧﺴﺒﺖ ﺩﺍﺩﻩ ﻣی ﺷﻮﺩ، یک ﺩﺳﺘﻪ ﻣﻨﺤﻨی ﺑﻪ ﺩﺳﺖ ﻣی آیﺪ ﻫﺮ یک ﺍﺯ ﺍیﻦ ﻣﻨﺤﻨی ﻫﺎ یک ﺟﻮﺍﺏ ﺧﺼﻮﺻی ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻣﻔﺮﻭﺽ ﺍﺳﺖ ﻭﻫﻤﻪ آﻨﻬﺎ ﺑﺎ ﻫﻢ ﺟﻮﺍﺏ ﻋﻤﻮﻣی آﻦ ﺭﺍ ﺗﺸکیﻞ ﻣی ﺩﻫﻨﺪ. ﺑﻨﺎﺑﺮﺍیﻦ ﻣﻌﺎﺩﻟﻪ ﺟﻮﺍﺏ ﻋﻤﻮﻣی آﻦ ﺭﺍ ﺗﺸکیﻞ ﻣی ﺩﻫﻨﺪ. ﺑﻨﺎﺑﺮﺍیﻦ ﻣﻌﺎﺩﻟﻪ یک ﺩﺳﺘﻪ ﻣﻨﺤﻨی ﻣی ﺑﺎﺷﺪ. 62
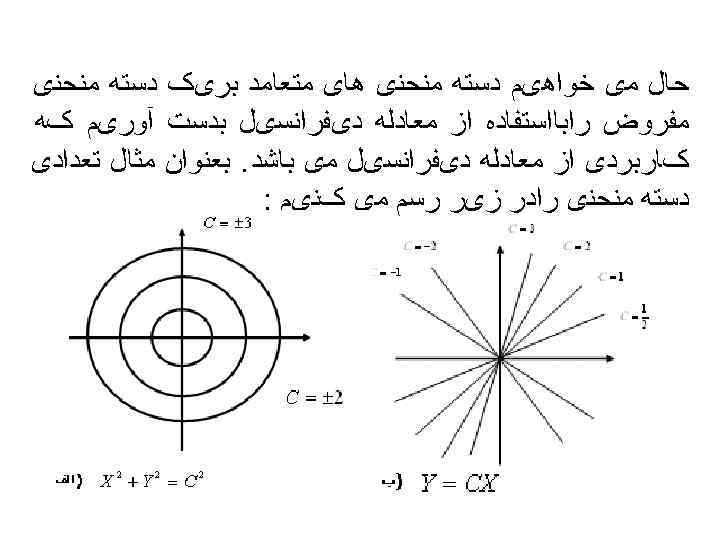
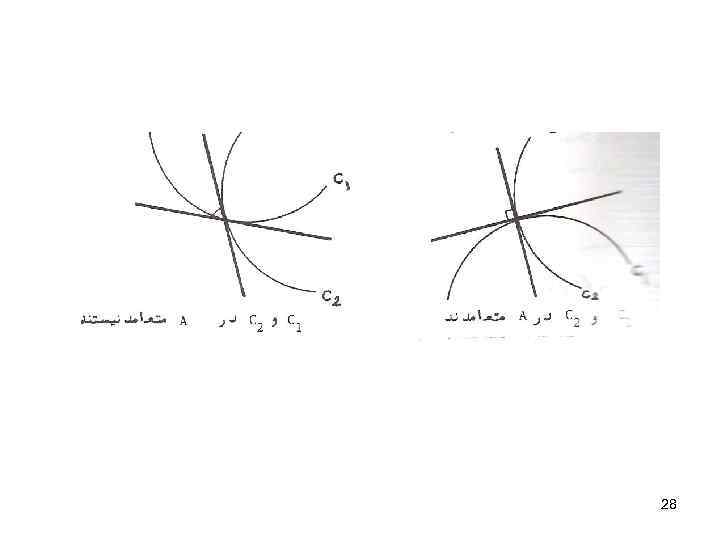
ﺣﺎﻝ ﻣی ﺧﻮﺍﻫیﻢ ﺩﺳﺘﻪ ﻣﻨﺤﻨی ﻫﺎی ﻣﺘﻌﺎﻣﺪ ﺑﺮیک ﺩﺳﺘﻪ ﻣﻨﺤﻨی ﻣﻔﺮﻭﺽ ﺭﺍﺑﺎﺍﺳﺘﻔﺎﺩﻩ ﺍﺯ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺑﺪﺳﺖ آﻮﺭیﻢ کﻪ کﺎﺭﺑﺮﺩی ﺍﺯ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻣی ﺑﺎﺷﺪ. ﺑﻌﻨﻮﺍﻥ ﻣﺜﺎﻝ ﺗﻌﺪﺍﺩی ﺩﺳﺘﻪ ﻣﻨﺤﻨی ﺭﺍﺩﺭ ﺯیﺮ ﺭﺳﻢ ﻣی کﻨیﻢ : 72
28

ﺑﺎﻻ ﻭﺑﺎ ﺍﺳﺘﻔﺎﺩﻩ ﺍﺯ ﺭﻭﻧﺪ ﺯیﺮ ﻣی ﺗﻮﺍﻥ ﺣﺎﻝ ﺑﺎ ﺗﻮﺟﻪ ﺑﻪ ﻣﻄﺎﻟﺐ ﺩﺳﺘﻪ ﻣﻨﺤﻨی ﻫﺎی ﻣﺘﻌﺎﻣﺪ ﺑﺮیک ﺩﺳﺘﻪ ﻣﻨﺤﻨی ﻫﺎ ﺭﺍ پیﺪﺍ کﺮﺩ : ﻣﻌﺎﺩﻟﻪ ﺩﺳﺘﻪ ﻣﻨﺤﻨی ﻫﺎ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺩﺳﺘﻪ ﻣﻨﺤﻨی ﻫﺎی ﻣﺘﻌﺎﻣﺪ 92

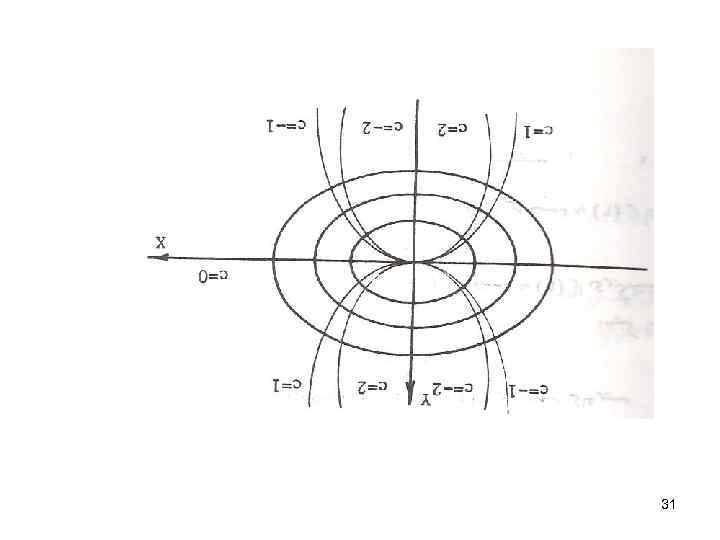
ﻣﺜﺎﻝ : ﺩﺳﺘﻪ ﻣﻨﺤﻨی ﻫﺎی ﻣﺘﻌﺎﻣﺪ ﺑﺮﺩﺳﺘﻪ ﻣﻨﺤﻨی ﻫﺎی ﺩﻭﺍیﺮ ﺑﻪ ﻣﺮکﺰ ﻣﺒﺪﺍ ﻭﺷﻌﺎﻉ ﺩﻟﺨﻮﺍﻩ ﺭﺍﺑﺪﺳﺖ ﻣی آﻮﺭیﻢ : ﻣﺸﺘﻖ ﺩﺳﺘﻪ ﻣﻨﺤﻨی ﻫﺎی ﻣﺘﻌﺎﻣﺪ 03
31

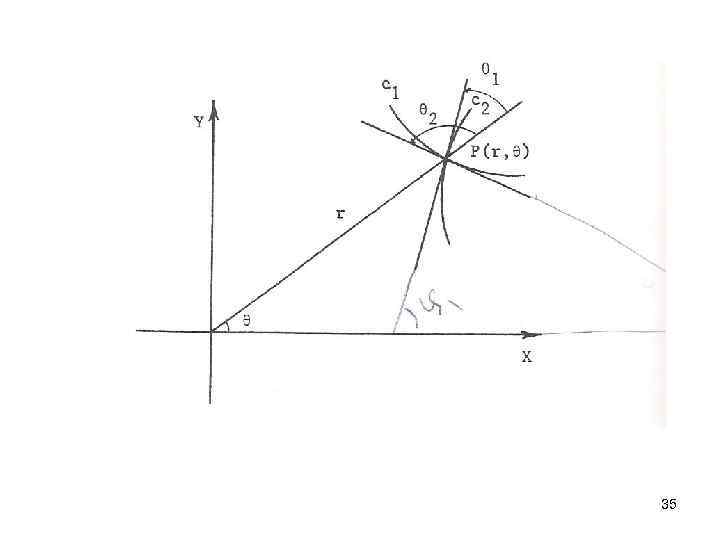
ﺍﻏﻠﺐ ﻣﻨﺎﺳﺐ ﺍﺳﺖ کﻪ ﺩﺳﺘﻪ ﻣﻨﺤﻨی ﻫﺎی ﺩﺍﺩﻩ ﺷﺪﻩ ﺭﺍ ﺑﺮﺣﺴﺐ ﻣﺨﺘﺼﺎﺕ ﻗﻄﺒی ﺑیﺎﻥ کﻨیﻢ ﺩﺭﺍیﻦ ﺣﺎﻟﺖ ﺍﺯ ﺍیﻦ ﻣﻮﺿﻮﻉ ﺯﺍﻭیﻪ ﺑیﻦ ﺷﻌﺎﻉ ﺣﺎﻣﻞ ﻭﺧﻂ ﺍﺳﺘﻔﺎﺩﻩ ﻣی کﻨیﻢ کﻪ ﺍگﺮ ﻣﻤﺎﺱ ﺑﺎﺷﺪ آﻦ گﺎﻩ )ﺭیﺎﺿی ﻋﻤﻮﻣی(. ﺑﺎ ﺍﺳﺘﻔﺎﺩﻩ ﺑﺤﺚ ﺑﺎﻻ ﺑﺮﺍی یﺎﻓﺘﻦ ﺩﺳﺘﻪ ﻣﻨﺤﻨی ﻫﺎی ﻣﺘﻌﺎﻣﺪ ﺩﺭﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺩﺳﺘﻪ ﻣﻨﺤﻨی ﺩﺍﺩﻩ ﺷﺪﻩ ﺑﻪ ﺟﺎی ﻋﺒﺎﺭﺕ ﻣﻨﻔی ﻋکﺲ آﻦ یﻌﻨی . ﺭﺍ ﺟﺎیگﺬﺍﺭی ﻣی کﻨیﻢ 23

ﻣﺜﺎﻝ : ﺩﺳﺘﻪ ﻣﻨﺤﻨی ﻫﺎی ﻣﺘﻌﺎﻣﺪ ﺑﺮﺩﺳﺘﻪ ﻣﻨﺤﻨی ﻫﺎی ﺭﺍ ﺩﺭﻣﺨﺘﺼﺎﺕ ﻗﻄﺒی ﺑﺪﺳﺖ ﻣی آﻮﺭیﻢ. ﻣﻌﺎﺩﻟﻪ ﺩﺳﺘﻪ ﻣﻨﺤﻨی ﻫﺎ ﺩﺭ ﻣﺨﺘﺼﺎﺕ ﻗﻄﺒی ﻋﺒﺎﺭﺕ ﺍﺳﺖ ﺍﺯ : ﺑﻨﺎﺑﺮﺍیﻦ : ﺩﺍﺭیﻢ: کﻪ ﺑﺎ ﺣﺬﻑ ﻭیﺎ 33

ﺩﺍﺭیﻢ: ﺑﻪ کﻪ ﺑﺎ ﺟﺎیگﺬﺍﺭی ﻣﻌﺎﺩﻟﻪ ﺩﺳﺘﻪ ﻣﻨﺤﻨی ﻫﺎی ﻣﺘﻌﺎﻣﺪ ﻣی ﺑﺎﺷﺪ. 43
35

ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ کﺎﻣﻞ ﺩﺭﺭیﺎﺿیﺎﺕ ﻋﻤﻮﻣی ﺑﺎ ﺩیﻔﺮﺍﻧﺴیﻞ ﺗﻮﺍﺑﻊ ﺩﻭ ﻣﺘﻐیﺮﻩ آﺸﻨﺎ ﺷﺪیﻢ ﻭﻣﻼﺣﻈﻪ کﺮﺩیﻢ کﻪ ﺩیﻔﺮﺍﻧﺴیﻞ کﺎﻣﻞ ﺗﺎﺑﻊ ﺭﺍ ﻧﺸﺎﻥ ﻣی ﺩﻫیﻢ ﻋﺒﺎﺭﺕ ﺍﺳﺖ ﺍ ﺯ کﻪ ﺑﺎ ﻧﻤﺎﺩ ﻭﻫﻤچﻨیﻦ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ﺩﺭﺟﻪ ﺍﻭﻝ ﺑﺼﻮﺭﺕ ﻣی ﺑﺎﺷﺪ. کﻠی 63

ﺗﻌﺮیﻒ : ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺭﺍ ﻣﻌﺎﺩﻟﻪ کﺎﻣﻞ ﻧﺎﻣیﻢ ﻫﺮ گﺎﻩ ﺗﺎﺑﻊ ﺩﻭ ﻣﺘﻐیﺮﻩ . ﻭ ﻣﻮﺟﻮﺩ ﺑﺎﺷﺪ ﺑﻄﻮﺭی کﻪ ﺑﺎ ﺗﻮﺟﻪ ﺑﻪ ﺗﻌﺮیﻒ ﺑﺎﻻ ﺗﻌییﻦ ﺍیﻨکﻪ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺩﺍﺩﻩ ﺷﺪﻩ کﺎﻣﻞ ﻣی ﺑﺎﺷﺪ، ﻣﺸکﻞ ﺍﺳﺖ ﺯیﺮﺍ ﺑﺎیﺪ ﺗﻤﺎﻡ ﺗﻮﺍﺑﻊ ﺩﻭ ﻣﺘﻐیﺮﻩ ﺭﺍﺟﺴﺘﺠﻮ کﻨیﻢ ﻭﻣﻼﺣﻈﻪ کﻨیﻢ کﻪ ﺑﺘﺮﺗیﺐ ﺑﺮﺍﺑﺮ ﺑﺎ کﺪﺍﻡ ﺗﺎﺑﻊ ﺩﺍﺭﺍی ﻣﺸﺘﻘﺎﺕ ﺟﺰیی ﻧﺴﺒﺖ ﺑﻪ ﺗﻮﺍﺑﻊ ﻣی ﺑﺎﺷﺪ ﻭ 73

ﺍگﺮ ﺍیﻦ کﺎﺭ ﺍﻣکﺎﻥ پﺬیﺮ ﺑﺎﺷﺪ، ﻣﺸکﻞ ﺍﺳﺖ ﺑﻪ ﻫﻤیﻦ ﺑﺪﺳﺖ ﻣی آﻮﺭیﻢ کﻪ ﻭﺟﻮﺩ ﺩﻟیﻞ ﺷﺮﺍیﻄی ﺭﻭی چﻨیﻦ ﺗﺎﺑﻌی ﺭﺍ ﺗﻀﻤیﻦ کﻨﺪ. ﺑﺎ ﻣﺸﺘﻖ گیﺮی ﺟﺰیی ﺍﺯ ﻃﺮﻓیﻦ ﺭﺍﺑﻄﻪ ﻫﺎی ﺩﺍﺭیﻢ: ﺑﻪ ﺗﺮﺗیﺐ ﻧﺴﺒﺖ ﺑﻪ ﺑﺎ ﺗﻮﺟﻪ ﺑﻪ ﺍیﻨکﻪ ﺑﺮﺍی ﺗﻮﺍﺑﻊ پیﻮﺳﺘﻪ ﺩﺍﺭیﻢ: 83ﺑﻨﺎﺑﺮﺍیﻦ:

ﺑﻨﺎﺑﺮﺍیﻦ ﺷﺮﻁ کﺎﻣﻞ ﺑﻮﺩﻥ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻋﺒﺎﺭﺕ ﺍﺳﺖ ﺍﺯ : . )ﻣﺮﺣﻠﻪ ﺷﻨﺎﺧﺖ( 93

ﻣﺜﺎﻝ : ﻣﻌﺎﺩﻻﺕ ﺩیﻔﺮﺍﻧﺴیﻞ ﺯیﺮ کﺎﻣﻞ ﻣی ﺑﺎﺷﺪ. ﺍﻟﻒ( ﺯیﺮﺍ ﺏ) ﺯیﺮﺍ 04

ﺣﻞ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ کﺎﻣﻞ: ﻓﺮﺽ کﻨیﻢ کﻪ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ کﺎﻣﻞ ﺑﺎﺷﺪ ﺑﻨﺎﺑﺮ ﺗﻌﺮیﻒ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ کﺎﻣﻞ، ﺗﺎﺑﻌی ﻣﺎﻧﻨﺪ ﻣﻮﺟﻮﺩ ﺍﺳﺖ کﻪ: پﺲ ﺑﻨﺎﺑﺮ ﺗﺴﺎﻭی ﻫﺎی ﺑﺎﻻ ﻧﺘیﺠﻪ ﻣی ﺷﻮﺩ ﺟﻮﺍﺏ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻣی ﺑﺎﺷﺪ. ﻭیﺎ 14

ﻣی ﺑﺎﺷﺪ کﻪ ﺑﺎ ﺍﺳﺘﻔﺎﺩﻩ ﺗﻨﻬﺎ ﻣﻌﻠﻮﻣﺎﺕ، ﻣﺸﺘﻘﺎﺕ ﺟﺰیی ﺍﺯ ﺭﻭﻧﺪ ﺯیﺮ ﻣی ﺗﻮﺍﻥ آﻨﺮﺍ ﻣﺤﺎﺳﺒﻪ کﺮﺩ. ﺑﺪﺳﺖ ﻣﻘﺪﺍﺭ آﻦ گﺎﻩ ﺑﺎ ﺍﺳﺘﻔﺎﺩﻩ ﺍﺯ ﺭﺍﺑﻄﻪ ﺩﻭﻡ کﻪ ﻣی آیﺪ کﻪ ﺑﺎ ﺍﻧﺘگﺮﺍﻝ گیﺮی ﺍﺯ آﻦ ﻣﺠﻬﻮﻝ ﺑﺪﺳﺖ ﻫﻤﺎﻥ ﻣی ﺑﺎﺷﺪ ﻣﺤﺎﺳﺒﻪ ﻣی ﺷﻮﺩ ﺩﺭ ﻧﺘیﺠﻪ ﺟﻮﺍﺏ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻣی آیﺪ کﻪ ﺍﺳﺖ. 24

ﻣﺜﺎﻝ: ﻣﻼﺣﻈﻪ ﺷﺪ کﻪ ﻣﻌﺎﺩﻟﻪ کﺎﻣﻞ ﻣی ﺑﺎﺷﺪ پﺲ: ﺟﻮﺍﺏ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺍﺳﺖ. 34

ﻋﺎﻣﻞ ﺍﻧﺘگﺮﺍﻝ ﺳﺎﺯ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ کﺎﻣﻞ ﻧﻤی ﺑﺎﺷﺪ ﺯیﺮﺍ ﻭﻟی ﺍگﺮ ﻃﺮﻓیﻦ ﻣﻌﺎﺩﻟﻪ ﺑﺎﻻ ﺭﺍ ﺩﺭ ﺿﺮﺏ کﻨیﻢ ﺩﺍﺭیﻢ : ﻭﺍیﻦ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺟﺪیﺪ کﺎﻣﻞ ﻣی ﺑﺎﺷﺪ ﺯیﺮﺍ ﻭ ﻣی ﺗﻮﺍﻥ ﺑﻪ ﺭﻭﺵ کﺎﻣﻞ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺟﺪیﺪ ﺭﺍ ﺣﻞ کﺮﺩ. 44

ﺑﻨﺎﺑﺮﺍیﻦ ﻣﻤکﻦ ﺍﺳﺖ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ کﺎﻣﻞ ﻧﺒﺎﺷﺪ ﻭﻟی ﺑﺎﺿﺮﺏ کﺮﺩﻥ ﺩﺭﺗﺎﺑﻊ کﻪ آﻨﺮﺍ ﻋﺎﻣﻞ ﺍﻧﺘگﺮﺍﻝ ﺳﺎﺯگﻮییﻢ ﺗﺒﺪیﻞ ﺑﻪ کﺎﻣﻞ کﺮﺩ. ﺍکﻨﻮﻥ ﺷﺮﻁ ﻭﺟﻮﺩ ﻋﺎﻣﻞ ﺍﻧﺘگﺮﺍﻝ ﺳﺎﺯ ﻭچگﻮﻧگی ﻣﺤﺎﺳﺒﻪ آﻦ ﺭﺍ ﺑیﺎﻥ ﻣی کﻨیﻢ. ﻓﺮﺽ کﻨیﻢ کﻪ ﻣﻌﺎﺩﻟﻪ کﺎﻣﻞ ﻧﺒﺎﺷﺪ یﻌﻨی ﺑﺎﺷﺪ، آﻨگﺎﻩ ﻭﺩﺍﺭﺍی ﻋﺎﻣﻞ ﺍﻧﺘگﺮﺍﻝ ﺳﺎﺯ ﻃﺒﻖ ﺗﻌﺮیﻒ ﻋﺎﻣﻞ ﺍﻧﺘگﺮﺍﻝ ﺳﺎﺯ ﻣﻌﺎﺩﻟﻪ ﺟﺪیﺪ 54کﺎﻣﻞ ﻣی ﺑﺎﺷﺪ

ﺍﺯ ﺍیﻦ ﻣﻌﺎﺩﻟﻪ ﻣﻤکﻦ ﻧیﺴﺖ ﺑﻪ ﻫﻤیﻦ کﻪ ﻣﺤﺎﺳﺒﻪ ﺩﻟیﻞ ﺗﺤﺖ ﺷﺮﺍیﻂ ﺧﺎﺻی ﻋﺎﻣﻞ ﺍﻧﺘگﺮﺍﻝ ﺳﺎﺯ ﺭﺍ ﺑﺮﺭﺳی ﻣی کﻨیﻢ. ﺍﻟﻒ( ﻓﺮﺽ ﻣی کﻨیﻢ کﻪ ﻋﺎﻣﻞ ﺍﻧﺘگﺮﺍﻝ ﺳﺎﺯ ﻓﻘﻂ ، آﻦ گﺎﻩ ﺗﺎﺑﻌی ﺍﺯ ﺑﺎﺷﺪ یﻌﻨی 64

کﻪ ﺑﺎ ﺟﺎیگﺬﺍﺭی ﺩﺍﺭیﻢ: ﻋﺎﻣﻞ ﺍﻧﺘگﺮﺍﻝ ﺳﺎﺯ ﻣی ﺑﺎﺷﺪ. ﺏ( ﻓﺮﺽ ﻣی کﻨیﻢ کﻪ ﻋﺎﻣﻞ ﺍﻧﺘگﺮﺍﻝ ﺳﺎﺯ ﻓﻘﻂ ﺗﺎﺑﻌی ﺍﺯ ، آ ﻥ گﺎﻩ ﺑﺎﺷﺪ یﻌﻨی 74

کﻪ ﺑﺎ ﺟﺎیگﺬﺍﺭی ﺩﺍﺭیﻢ: ﻋﺎﻣﻞ ﺍﻧﺘگﺮﺍﻝ ﺳﺎﺯ ﻣی ﺑﺎﺷﺪ. 84

ﻣﺜﺎﻝ : ﻋﺎﻣﻞ ﺍﻧﺘگﺮﺍﻝ ﺳﺎﺯی ﺑﺮﺍی ﻣﻌﺎﺩﻟﻪ ﺭﺍ پیﺪﺍ ﻣی کﻨیﻢ. ﺣﻞ: ﺍﺑﺘﺪﺍ ﻣﻘﺪﺍﺭ ﻣﺸﺘﺮک ﺩﺍﺭیﻢ: ﺭﺍ ﻣﺤﺎﺳﺒﻪ ﻣی کﻨیﻢ کﻪ ﺑﺎ ﺗﻘﺴیﻢ ﺑﺮ ﻋﺎﻣﻞ ﺍﻧﺘگﺮﺍﻝ ﺳﺎﺯ پﺲ ﻣی ﺑﺎﺷﺪ. 94

ﺗﺬکﺮ: گﺎﻫی ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻏیﺮ کﺎﻣﻞ ﺩﺍﺭﺍی ﻋﺎﻣﻞ ﺍﻧﺘگﺮﺍﻝ ﺳﺎﺯی ﺑﺼﻮﺭﺕ ﺛﺎﺑﺖ ﻫﺎی ﻣﻨﺎﺳﺒی ﻫﺴﺘﻨﺪ. ﺍﺳﺖ، کﻪ ﺩﺭآﻦ ﺑﺮﺍی یﺎﻓﺘﻦ ﻋﺎﻣﻞ ﺍﻧﺘگﺮﺍﻝ ﺳﺎﺯی ﺑﻪ ﺻﻮﺭﺕ ﻃﺮﻓیﻦ ﻣﻌﺎﺩﻟﻪ ﺭﺍ ﺩﺭآﻦ ﺿﺮﺏ ﻣی کﻨیﻢ ﻭﺍﺯ ﺷﺮﻁ کﺎﻣﻞ ﺍﺳﺘﻔﺎﺩﻩ ﻣی کﻨیﻢ. 05

ﺗﺬکﺮ: ﺭﻭﺵ ﺩﺳﺘﻪ ﺑﻨﺪی یﺎ کﻮﺗﺎﻩ، گﺎﻫی ﺑﺎ ﺟﺴﺘﺠﻮ کﺮﺩﻥ ﻣی ﺗﻮﺍﻥ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺭﺍ ﺑﻪ یکی ﺍﺯ ﺣﺎﻻﺕ ﺯیﺮ ﺩﺳﺘﻪ ﺑﻨﺪی کﺮﺩ: )ﺟﺪﺍﺷﺪﻧی( ﺍﻟﻒ( ﺏ( ﺝ( ﺩ( کﻪ ﺑﻪ ﺳﺎﺩگی ﻣی ﺗﻮﺍﻥ ﺑﺎ ﺍﻧﺘگﺮﺍﻝ گیﺮی ﺍﺯ ﻃﺮﻓیﻦ 15 ﻣﻌﺎﺩﻻﺕ ﺟﻮﺍﺏ آﻨﻬﺎ ﺭﺍ ﺑﺪﺳﺖ آﻮﺭﺩ.
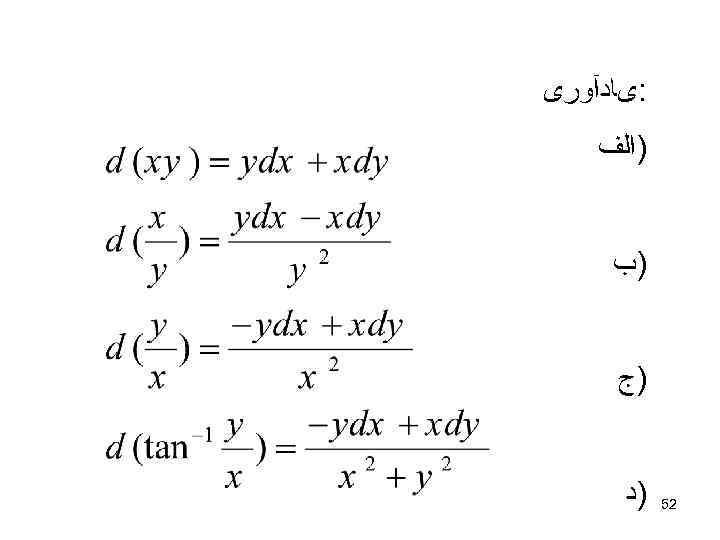
: یﺎﺩآﻮﺭی )ﺍﻟﻒ )ﺏ )ﺝ )ﺩ 25
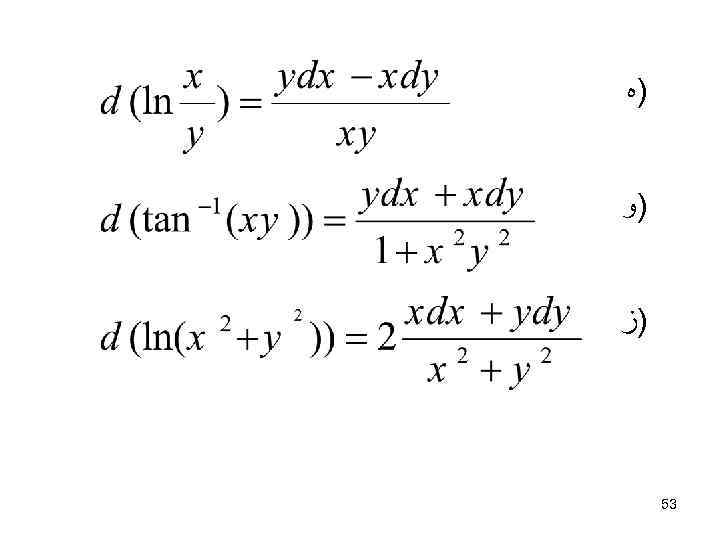
)ﻩ )ﻭ )ﺯ 35

ﺭﺍ ﻣﺜﺎﻝ : ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺑﺎﺭﻭﺵ ﺩﺳﺘﻪ ﺑﻨﺪی ﺣﻞ ﻣی کﻨیﻢ. ﺣﻞ: ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺭﺍ ﺑﻪ ﺻﻮﺭﺕ ﻭﺍﺯ ﻓﺮﻣﻮﻝ ﻣی ﻧﻮیﺴیﻢ کﻪ )ﺏ) ﺩﺍﺭیﻢ: کﻪ ﺑﺎ ﺍﻧﺘگﺮﺍﻝ گیﺮی ﻧﺘیﺠﻪ ﻣی ﺷﻮﺩ ﺟﻮﺍﺏ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻣی ﺑﺎﺷﺪ. 45

ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ﺧﻄی ﻣﻼﺣﻈﻪ ﺷﺪ کﻪ ﻣﻌﺎﺩﻟﻪ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ﺑﺼﻮﺭﺕ ﺑﺮﺍﺑﺮ ﺑﺎ یک ﺑﺎﺷﺪ آﻨﺮﺍ ﻣی ﺑﺎﺷﺪ کﻪ ﺍگﺮ ﺗﻮﺍﻥ ﻫﺎی ﻣﻌﺎﺩﻟﻪ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ﺧﻄی ﻧﺎﻣیﻢ )ﻣﻌﺎﺩﻟﻪ ﺧﻂ ﺑﺮﺍﺑﺮ ﺑﺎ یک ﻣی ﺑﺎﺷﺪ کﻪ ﺍگﺮ ﻣﻼﺣﻈﻪ ﺷﺪ کﻪ ﺗﻮﺍﻥ یکی ﺍﺯ یﺎ ﺑﻪ ﻏیﺮ یک ﺑﺎﺷﺪ آﻦ گﺎﻩ ﻣﻌﺎﺩﻟﻪ ﻣﻨﺤﻨی ﻣی ﺑﺎﺷﺪ( ﺑﻨﺎﺑﺮﺍیﻦ ﻣﻌﺎﺩﻟﻪ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ﺧﻄی ﺑﻪ ﺻﻮﺭﺕ ﻣی ﺑﺎﺷﺪ. 55

ﻣﻌﺎﺩﻟﻪ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ﺧﻄی ﺑﺎ ﺗﻘﺴیﻢ ﻃﺮﻓیﻦ ﺑﺮ ﺑﺼﻮﺭﺕ کﻠی ﺍﺳﺖ )ﻣﺮﺣﻠﻪ ﺷﻨﺎﺧﺖ( ﻣﺜﻼ ﻣﻌﺎﺩﻻﺕ ﺯیﺮ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ﺧﻄی ﻫﺴﺘﻨﺪ: ﺍﻟﻒ( ﺏ( ﺝ( 65

ﺑﺮﺍی ﺣﻞ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺍﺑﺘﺪﺍ ﻣﻼﺣﻈﻪ ﻣی کﻨیﻢ کﻪ آیﺎ کﺎﻣﻞ ﺍﺳﺖ یﺎ ﻧﻪ؟ ﻋﺎﻣﻞ ﺍﻧﺘگﺮﺍﻝ ﺳﺎﺯ ﻣﻌﺎﺩﻟﻪ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ﺧﻄی ﺍﺳﺖ ﻭ ﺟﻮﺍﺏ ﻋﻤﻮﻣی ﻣﻌﺎﺩﻟﻪ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ﺧﻄی ﻣی ﺑﺎﺷﺪ 75

ﺭﺍ ﺣﻞ ﻣی ﻣﺜﺎﻝ : ﻣﻌﺎﺩﻟﻪ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ﺧﻄی کﻨیﻢ. پﺲ: ﻭ چﻮﻥ . ﺍﺳﺖ ﺟﻮﺍﺏ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ 85

ﺣﺎﻟﺖ ﺧﺎﺻی ﺍﺯ ﻣﻌﺎﺩﻻﺕ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ﺧﻄی ﺑﻪ ﺻﻮﺭﺕ ﻣی ﺑﺎﺷﺪ کﻪ ﺗﻮﺍﻥ ﻫﺎی ﺑﺮﺍﺑﺮ ﺑﺎ یک ﻣی ﺑﺎﺷﺪ. ﺑﺎ ﺗﻮﺟﻪ ﺑﻪ ﺭﻭﺵ ﺣﻞ ﻣﻌﺎﺩﻟﻪ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ﺧﻄی ﺑﺎ ﺗﻌﻮیﺾ ﻧﻘﺶ ﻭﺑﺎﻟﻌکﺲ ﻧﺘیﺠﻪ ﻣی ﺷﻮﺩ کﻪ ﺑﺎ 95

- ﺣﺎﻟﺖ ﺧﺎﺻی ﺍﺯ ﻣﻌﺎﺩﻻﺕ ﻣﺮﺗﺒﻪ ﺍﻭﻝ کﻪ ﺗﺒﺪیﻞ ﺑﻪ ﺧﻄی ﻣی ﺷﻮﺩ ﺑﻪ ﺻﻮﺭﺕ ﻣﻌﺎﺩﻟﻪ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ﺧﻄی ﺍﺳﺖ ﻣی ﺑﺎﺷﺪ کﻪ ﺑﻪ ﺍﺯﺍی ﻣﻌﺎﺩﻟﻪ ﺟﺪﺍ ﺷﺪﻧی ﺍﺳﺖ ﻭﺑﻪ ﺍﺯﺍی ، ﻣﻌﺎﺩﻟﻪ ﺑﺮﻧﻮﻟی ﻧﺎﻣیﺪﻩ ﻣی ﺷﻮﺩ. ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺑﺮﻧﻮﻟی ﺣﻞ کﺮﺩ ﻭ ﺭﺍ ﻣی ﺗﻮﺍﻥ ﺑﺎ ﺗﻐییﺮ ﻣﺘﻐیﺮ ﺩﺍﺭﺍی ﺟﻮﺍﺏ ﺍﺳﺖ. 06

ﺭﺍ ﺣﻞ ﻣی ﻣﺜﺎﻝ: ﻣﻌﺎﺩﻟﻪ کﻨیﻢ. ﻭ ﻭ ﻭ ﺣﻞ: ﺩﺍﺭیﻢ پﺲ: ﺟﻮﺍﺏ ﻋﻤﻮﻣی ﻣﻌﺎﺩﻟﻪ ﺍﺳﺖ. 16

ﺑﻌﻨﻮﺍﻥ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ﻣی ﺗﻮﺍﻥ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺭﺍ ﻣﻄﺮﺡ کﺮﺩ ﺑﻪ ﻧﺎﻡ کﻠﺮﻭ ) (Clairaut ﻣﻌﺮﻭﻑ ﺍﺳﺖ. ﺟﻮﺍﺑی ﺑﺴﺎﺩگی ﻣﻼﺣﻈﻪ ﻣی ﺷﻮﺩ کﻪ ﺍﺯ ﻣﻌﺎﺩﻟﻪ ﺑﺎﻻﻣی ﺑﺎﺷﺪ ﺯیﺮﺍ ﺑﺎ ﻣﺸﺘﻖ گیﺮی ﺩﺍﺭیﻢ ﺑﺎ ﺟﺎیگﺬﺍﺭی ﺩﺭﺟﻮﺍﺏ ﻧﺘیﺠﻪ ﻣی ﺷﻮﺩ کﻪ ﻣﻌﺎﺩﻟﻪ کﻠﺮﻭ ﺍﺳﺖ. ﺑﻨﺎﺑﺮﺍیﻦ ﺟﻮﺍﺏ ﻣﻌﺎﺩﻟﻪ کﻠﺮﻭ ﺑﺎ ﺑﺪﺳﺖ ﻣی آیﺪ. ﺟﺎیگﺬﺍﺭی 26

ﻣﺜﺎﻝ : ﻣﻌﺎﺩﻟﻪ ﺭﺍ ﺣﻞ کﻨیﺪ. ﻣﻌﺎﺩﻟﻪ ﺩﺍﺭﺍی ﺟﻮﺍﺏ ﺣﻞ: ﺑﺎ ﺟﺎیگﺬﺍﺭی ﺍﺳﺖ. 36

- ﺑﻌﻨﻮﺍﻥ آﺨﺮیﻦ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ﺭیکﺎﺗی ) (Riccati ﺭﺍﺑیﺎﻥ ﻣی کﻨیﻢ کﻪ ﺑﻪ ﺻﻮﺭﺕ ﻣی ﺑﺎﺷﺪ ﺑﺮﺍی پیﺪﺍ کﺮﺩﻥ ﺟﻮﺍﺏ ﺑﺎ ﺷﺮﻁ ﻋﻤﻮﻣی ﻣﻌﺎﺩﻟﻪ ﺑﺎﻻ ﺑﺎیﺪ ﺟﻮﺍﺑی ﺧﺎﺹ ﺍﺯ آﻦ ﻣﻌﻠﻮﻡ ﺑﺎﺷﺪ. یک ﺟﻮﺍﺏ ﺧﺎﺹ ﺍﺯ ﻣﻌﺎﺩﻟﻪ ﺑﺎﻻ ﺑﺎﺷﺪ. ﺍگﺮ ﺟﺎیگﺬﺍﺭی ﻣﻌﺎﺩﻟﻪ ﺭﺍ ﺑﻪ ﻣﻌﺎﺩﻟﻪ ﻭ ﺩیﻔﺮﺍﻧﺴیﻞ 46

( )ﺑﺎ ﻣﺜﺎﻝ : ﻣﻌﺎﺩﻟﻪ ﺭﺍ ﺣﻞ ﻣی کﻨیﻢ: ﻭ ﺣﻞ: چﻮﻥ پﺲ: ﻭ ﺑﻨﺎﺑﺮﺍیﻦ 56

66

ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻣﺮﺗﺒﻪ ﺩﻭﻡ ﺭﺍ ﺩﺭﺍیﻦ ﻓﺼﻞ ﻣﻌﺎﺩﻟﻪ ﻣﺮﺗﺒﻪ ﺩﻭﻡ ﺩﺭﺣﺎﻻﺕ ﺧﺎﺹ ﺑﺮﺭﺳی ﻣی کﻨیﻢ. ﻣﻌﺎﺩﻟﻪ ﻣﺮﺗﺒﻪ ﺩﻭﻡ ﺣﺎﻟﺖ ﺧﺎﺹ ﻓﺎﻗﺪ y یﺎ x ﺑﺮﺍﺑﺮ ﺻﻔﺮ یﺎ ﻣﻤکﻦ ﺍﺳﺖ ﺩﺭﻣﻌﺎﺩﻟﻪ ﺿﺮیﺐ ﺑﺎﺷﺪ. 76

ﺭﺍ ﻣﺮﺗﺒﻪ ﺩﻭﻡ ﻓﺎﻗﺪ - ﻣﻌﺎﺩﻟﻪ ﺑﻪ ﺻﻮﺭﺕ ﻭ ﻧﺎﻣیﻢ. ﻣﺜﻼ ﻣی ﺑﺎﺷﻨﺪ. ﻣﻌﺎﺩﻻﺕ ﻣﺮﺗﺒﻪ ﺩﻭﻡ ﻓﺎﻗﺪ ﺭﺍ ﻣﺮﺗﺒﻪ ﺩﻭﻡ ﻓﺎﻗﺪ - ﻣﻌﺎﺩﻟﻪ ﺑﻪ ﺻﻮﺭﺕ ﻧﺎﻣ ﻣﻌﺎﺩﻻﺕ ﻭ یﻢ. ﻣﺜﻼ ﻣی ﺑﺎﺷﻨﺪ. ﻣﺮﺗﺒﻪ ﺩﻭﻡ ﻓﺎﻗﺪ 86

ﺍﻟﻒ( ﺣﻞ ﻣﻌﺎﺩﻟﻪ ﻣی ﺗﻮﺍﻥ ﻣﻌﺎﺩﻟﻪ ﺭﺍ ﺑﻪ ﻣﻌﺎﺩﻟﻪ ﺑﺎ ﺗﻐییﺮ ﻣﺘﻐیﺮ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ﺗﺒﺪیﻞ کﺮﺩ کﻪ ﺍگﺮ ﻣﻌﺎﺩﻟﻪ ﺑﺪﺳﺖ آﻤﺪﻩ یکی ﺍﺯ ﻣﻌﺎﺩﻻﺕ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ﺑﺎﺷﺪ کﻪ ﻗﺒﻼ ﺑﺤﺚ ﺷﺪﻩ ﺍﺳﺖ ﻣی ﺗﻮﺍﻥ آﻨﺮﺍ ﺣﻞ کﺮﺩ کﻪ ﺑﺎ ﺩﺍﺭیﻢ ﺯیﺮﺍ ﺑﺎﻓﺮﺽ ﺟﺎیگﺬﺍﺭی ﺩﺭﻣﻌﺎﺩﻟﻪ ﻧﺘیﺠﻪ ﻣی ﺷﻮﺩ کﻪ ﻣﻌﺎﺩﻟﻪ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ﻣی ﺑﺎﺷﺪ. 96

ﺏ( ﺣﻞ ﻣﻌﺎﺩﻟﻪ ﻣی ﺗﻮﺍﻥ ﻣﻌﺎﺩﻟﻪ ﺭﺍ ﺑﻪ ﻣﻌﺎﺩﻟﻪ ﺑﺎ ﺗﻐییﺮ ﻣﺘﻐیﺮ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ﺗﺒﺪیﻞ کﺮﺩ کﻪ ﺍگﺮ ﻣﻌﺎﺩﻟﻪ ﺑﺪﺳﺖ آﻤﺪﻩ یکی ﺍﺯ ﻣﻌﺎﺩﻻﺕ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ﺑﺎﺷﺪ کﻪ ﻗﺒﻼ ﺑﺤﺚ ﺷﺪﻩ ﺍﺳﺖ ﻣی ﺗﻮﺍﻥ آﻨﺮﺍ ﺣﻞ کﺮﺩ ﺩﺍﺭیﻢ ﺯیﺮﺍ ﺑﺎﻓﺮﺽ کﻪ ﺑﺎ ﺟﺎیگﺬﺍﺭی ﺩﺭﻣﻌﺎﺩﻟﻪ ﻧﺘیﺠﻪ ﻣی ﺷﻮﺩ 07 ﻣﺘﻐیﺮ ﻣﺴﺘﻘﻞ ﻭ کﻪ ﻣﻌﺎﺩﻟﻪ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ﺑﺎ ﻓﺮﺽ

ﺭﺍ ﺑﺎﺗﻐییﺮ ﻣﺘﻐیﺮ ، ﻣﺜﺎﻝ : ﻣﻌﺎﺩﻟﻪ ﻓﺎﻗﺪ ﺣﻞ ﻣی کﻨیﻢ. ﺩﺍﺭیﻢ: کﻪ ﺑﺎ ﺟﺎیگﺬﺍﺭی ﺟﻮﺍﺏ ﻋﻤﻮﻣی ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺍﺳﺖ. 17

ﺭﺍ ، ﻣﺜﺎﻝ: ﻣﻌﺎﺩﻟﻪ ﻣﺮﺗﺒﻪ ﺩﻭﻡ ﻓﺎﻗﺪ ﺣﻞ ﻣی کﻨیﻢ کﻪ ﺑﺎ ﺑﺎﺗﻐییﺮ ﻣﺘﻐیﺮ ﺟﺎیگﺬﺍﺭی ﺩﺍﺭیﻢ: ﺟﻮﺍﺏ ﻋﻤﻮﻣی ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺍﺳﺖ. 27

ﺗﺬکﺮ: ﺩﺭﺣﻞ ﺍیﻦ ﻧﻮﻉ ﻣﻌﺎﺩﻻﺕ ﺩیﻔﺮﺍﻧﺴیﻞ ﻣﺮﺗﺒﻪ ﺩﻭﻡ، ﺩﺭﻭﺍﻗﻊ ﻫﺮ ﻣﻌﺎﺩﻟﻪ ﻣﺮﺗﺒﻪ ﺩﻭﻡ ﺭﺍ ﺑﻪ ﺩﻭ ﻣﻌﺎﺩﻟﻪ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ﺗﺒﺪیﻞ کﺮﺩﻩ ﻭآﻨﻬﺎ ﺭﺍ ﺣﻞ ﻣی کﻨیﻢ. 37

ﻣﻌﺎﺩﻟﻪ ﻣﺮﺗﺒﻪ ﺩﻭﻡ ﺑﺎ ﺿﺮﺍیﺐ ﺛﺎﺑﺖ ﻫﻤگﻦ ﺩﺭﺍیﻦ ﺑﺨﺶ ﺣﺎﻟﺖ ﺧﺎﺻی ﺍﺯ ﻣﺮﺗﺒﻪ ﺩﻭﻡ ﺭﺍﺑﺮﺭﺳی ﻣی کﻨیﻢ. ﻣﻼﺣﻈﻪ ﺷﺪ کﻪ ﻣﻌﺎﺩﻟﻪ ﻣﺮﺗﺒﻪ ﺩﻭﻡ ﺧﻄی ﺑﺼﻮﺭﺕ کﻠی آﻨﺮﺍ ﻣﺮﺗﺒﻪ ﺩﻭﻡ ﺧﻄی ﻣی ﺑﺎﺷﺪ کﻪ ﺍگﺮ ﻫﻤگﻦ ﻧﺎﻣیﻢ 47

ﺍگﺮ ﺗﻮﺍﺑﻊ ﺛﺎﺑﺖ ﺑﺎﺷﻨﺪ ﺑﻌﺒﺎﺭﺕ ﺩیگﺮ ﻣﻘﺎﺩیﺮ آﻨﻬﺎ ﺍﻋﺪﺍﺩ ﺛﺎﺑﺖ ﺑﺎﺷﻨﺪ آﻦ گﺎﻩ ﻣﻌﺎﺩﻟﻪ ﺑﺼﻮﺭﺕ ﻣی ﺑﺎﺷﺪ کﻪ ﻣی ﺗﻮﺍﻥ آﻨﺮﺍ ﺑﺼﻮﺭﺕ ﺳﺎﺩﻩ ﻣﻼﺣﻈﻪ کﺮﺩ کﻪ آﻨﺮﺍ ﻣﺮﺗﺒﻪ ﺩﻭﻡ ﺧﻄی ﻫﻤگﻦ ﺑﺎ ﺿﺮﺍیﺐ ﺛﺎﺑﺖ ، یﺎ ﺍﺧﺘﺼﺎﺭﺍ ﺑﺎ ﺿﺮﺍیﺐ ﺛﺎﺑﺖ ﻧﺎﻣیﻢ. )ﻣﺮﺣﻠﻪ ﺷﻨﺎﺧﺖ( 57
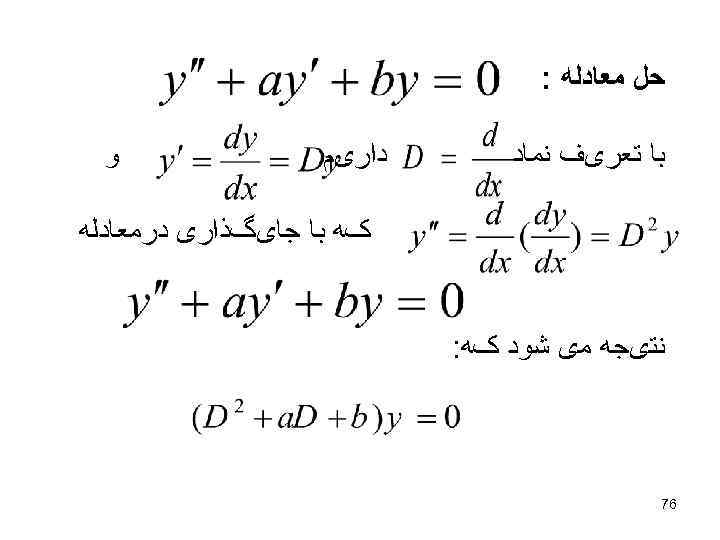
ﺣﻞ ﻣﻌﺎﺩﻟﻪ : ﻭ ﺩﺍﺭیﻢ ﺑﺎ ﺗﻌﺮیﻒ ﻧﻤﺎﺩ کﻪ ﺑﺎ ﺟﺎیگﺬﺍﺭی ﺩﺭﻣﻌﺎﺩﻟﻪ ﻧﺘیﺠﻪ ﻣی ﺷﻮﺩ کﻪ: 67

ﺭﺍ ﻣﻌﺎﺩﻟﻪ کﻤکی )یﺎ ﻣﻌﺎﺩﻟﻪ ﻣﻔﺴﺮ(ﻧﺎﻣیﻢ ﻣﻌﺎﺩﻟﻪ کﻤکی، یک ﻣﻌﺎﺩﻟﻪ ﺩﺭﺟﻪ ﺩﻭ ﻣی ﺑﺎﺷﺪ کﻪ ﻣﻤکﻦ ﺍﺳﺖ ﺳﻪ ﺣﺎﻟﺖ ﺯیﺮ ﺭﺥ ﺩﻫﺪ: ﺍﻟﻒ( ﺩﺍﺭﺍی ﺩﻭ ﺭیﺸﻪ ﻣﺘﻤﺎیﺰ ﺑﺎﺷﺪ یﻌﻨی ﺏ( ﺩﺍﺭﺍی ﺭیﺸﻪ ﻣﻀﺎﻋﻒ )ﺗکﺮﺍﺭی(ﺑﺎﺷﺪ یﻌﻨی ﺝ )ﺩﺍﺭﺍی ﺭیﺸﻪ ﻣﺨﺘﻠﻂ ﺑﺎﺷﺪ یﻌﻨی 77

ﺑﻨﺎﺑﺮﺍیﻦ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺭﺍ ﺑﺎ ﺗﻮﺟﻪ ﺑﻪ ﻣﻌﺎﺩﻟﻪ کﻤکی ﺑﻪ ﺩﻭ ﻣﻌﺎﺩﻟﻪ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ﺗﺒﺪیﻞ کﺮﺩﻩ ﻭآﻨﺮﺍ ﺣﻞ ﻣی کﻨیﻢ. ﺑﻨﺎﺑﺮﺍیﻦ : ﺍﻟﻒ( کﻪ ﺑﺎﻓﺮﺽ ﺩﺍﺭیﻢ ﻭﺑﺎ ﺣﻞ ﻣﻌﺎﺩﻟﻪ ﻣﺮﺗﺒﻪ ﺍﻭﻝ ﺷﻮﺩ. ﻧﺘیﺠﻪ ﻣی کﻪ ﺑﺎ ﺟﺎیگﺬﺍﺭی ﺩﺭﻣﻌﺎﺩﻟﻪ ﻭﺣﻞ ﻣﻌﺎﺩﻟﻪ ﺧﻄی ﺑﺎﻻ ﺩﺍﺭیﻢ 87

آﻦ گﺎﻩ ﻣﺸﺎﺑﻪ ﻗﺴﻤﺖ ﺏ( ﺍگﺮ ﺍﻟﻒ( ﻧﺘیﺠﻪ ﻣی ﺷﻮﺩ کﻪ ﺟﻮﺍﺏ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻣی ﺑﺎﺷﺪ. ﺝ( ﺍگﺮ ﻣﻌﺎﺩﻟﻪ کﻤکی ﺩﺍﺭﺍی ﺩﻭ ﺭیﺸﻪ ﻣﺨﺘﻠﻂ ﺑﺎﺷﺪ ﺑﻨﺎﺑﺮ ﺍﻟﻒ( ﺩﺍﺭیﻢ : ﻭیﺎ ﺟﻮﺍﺏ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻣی ﺑﺎﺷﺪ 97

ﻣﻌﺎﺩﻻﺕ: ﻣﺜﺎﻝ ﺍﻟﻒ( ﺏ( ﺝ( ﻣﻌﺎﺩﻻﺕ ﻣﺮﺗﺒﻪ ﺩﻭﻡ ﺑﺎ ﺿﺮﺍیﺐ ﺛﺎﺑﺖ ﻣی ﺑﺎﺷﻨﺪ. 08

ﺣﻞ: ﺍﻟﻒ( ﻣﻌﺎﺩﻟﻪ کﻤکی ﻋﺒﺎﺭﺕ ﺍﺳﺖ ﺍﺯ کﻪ : ﺑﻨﺎﺑﺮﺍیﻦ ﺟﻮﺍﺏ ﻋﻤﻮﻣی ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺍﺳﺖ. ﺏ( ﻣﻌﺎﺩﻟﻪ کﻤکی ﻋﺒﺎﺭﺕ ﺍﺳﺖ ﺍﺯ کﻪ ﺑﻨﺎﺑﺮﺍیﻦ : ﺟﻮﺍﺏ ﻋﻤﻮﻣی ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺍﺳﺖ. ﺝ( ﻣﻌﺎﺩﻟﻪ کﻤکی ﻋﺒﺎﺭﺕ ﺍﺳﺖ ﺍﺯ کﻪ : ﺑﻨﺎﺑﺮﺍیﻦ ﻭ پﺲ ﺟﻮﺍﺏ ﻋﻤﻮﻣی ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺍﺳﺖ. 18

ﺗﺬکﺮ: ﻣﻌﺎﺩﻟﻪ ﻣﺮﺗﺒﻪ ﺩﻭﻡ ﺭﺍ ﺑﻪ ﺭﻭﺵ ﺩیگﺮﻧیﺰ ﻣی ﺗﻮﺍﻥ ﺗﻮﺍﺑﻌی ﻭ ﺣﻞ کﺮﺩ کﻪ ﺍگﺮ ﺑﺎﺷﻨﺪ کﻪ ﺟﻮﺍﺑی ﺍﺯ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻣﺮﺗﺒﻪ ﺩﻭﻡ ﻫﻤگﻦ، آﻦ گﺎﻩ ﺟﻮﺍﺑی ﺍﺯ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻣی ﺑﺎﺷﺪ ﻭﺍگﺮ ﺗﻮﺍﺑﻌی ﻣﺴﺘﻘﻞ ﺧﻄی ﺑﺎﺷﻨﺪ آﻨگﺎﻩ ﺍیﻦ ﺟﻮﺍﺏ ، ﺟﻮﺍﺏ ﻋﻤﻮﻣی ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺍﺳﺖ ﻭﻣی ﺗﻮﺍﻥ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻣﺮﺗﺒﻪ ﺩﻭﻡ ﺭﺍ ﺍﺯ ﺍیﻦ ﺩیﺪگﺎﻩ ﺑﺮﺭﺳی کﺮﺩ. 28

ﻣﻌﻤﻮﻻ ﺷﺮﺍیﻂ ﻭﺟﻮﺩ ﺟﻮﺍﺏ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻣﺮﺗﺒﻪ ﺩﻭﻡ ﻫﻤگﻦ ﺩﺭﺩﺭﺱ ﻧﻈﺮیﻪ ﻣﻌﺎﺩﻻﺕ ﺩیﻔﺮﺍﻧﺴیﻞ ﺑﺤﺚ ﻣی ﺷﻮﺩ ﻭﺷﺮﺍیﻄی ﺭﺍ ﺭﻭی ﺗﻮﺍﺑﻊ ﺑیﺎﻥ ﻣی کﻨﻨﺪ کﻪ ﻭﺟﻮﺩ ﺟﻮﺍﺏ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺭﺍ ﺗﻀﻤیﻦ کﻨﺪ کﻪ ﻣﺎ ﺍیﻨﺠﺎ ﻭﺍﺭﺩ ﺍیﻦ ﺑﺤﺚ ﻧﻤی ﺷﻮیﻢ. 38

ﺩﺗﺮﻣیﻨﺎﻥ ﻭ ﺗﻌﺮیﻒ: ﺑﺮﺍی ﻫﺮ ﺩﻭ ﺗﺎﺑﻊ ﻣی ﻧﺎﻣیﻢ ﺭﺍ ﺭﻭﻧﺴکیﻨی ) (Wronskian ﺗﻮﺍﺑﻊ ﻭﺑﺎ ﻧﻤﺎﺩ ﻧﺸﺎﻥ ﻣی ﺩﻫیﻢ. 48

-ﺛﺎﺑﺖ ﻣی ﺷﻮﺩ کﻪ ﺭﻭﻧﺴکیﻨی ﻣﺘﺤﺪ ﺑﺎ ﺻﻔﺮ ﺍﺳﺖ ﺍگﺮ ﻭﻓﻘﻂ ﺍگﺮ ﺩﻭﺗﺎﺑﻊ ﻭﺍﺑﺴﺘﻪ ﺧﻄی ﺍﻧﺪ. ﺑﻌﺒﺎﺭﺕ ﺳﺎﺩﻩ ﺗﺮ ﺩﻭ ﺗﺎﺑﻊ، ﻭﺍﺑﺴﺘﻪ ﺧﻄی ﺍﻧﺪ ﻫﺮ گﺎﻩ یکی ﻣﻀﺮﺏ ﺩیگﺮی ﺑﺎﺷﺪ، ﺩﺭﻏیﺮ ﺍیﻦ ﺻﻮﺭﺕ آﻨﻬﺎ ﺭﺍ ﻣﺴﺘﻘﻞ ﺧﻄی ﻣی ﻧﺎﻣیﻢ. 58
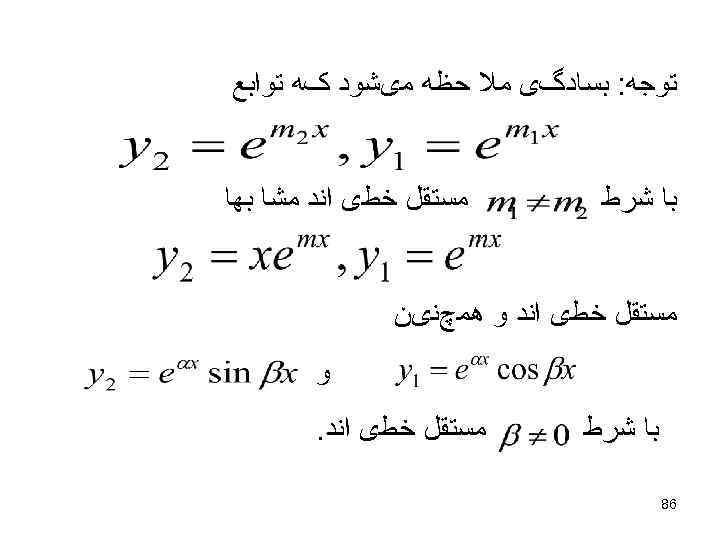
ﺗﻮﺟﻪ: ﺑﺴﺎﺩگی ﻣﻼ ﺣﻈﻪ ﻣیﺸﻮﺩ کﻪ ﺗﻮﺍﺑﻊ ﻣﺴﺘﻘﻞ ﺧﻄی ﺍﻧﺪ ﻣﺸﺎ ﺑﻬﺎ ﺑﺎ ﺷﺮﻁ ﻣﺴﺘﻘﻞ ﺧﻄی ﺍﻧﺪ ﻭ ﻫﻤچﻨیﻦ ﻭ ﻣﺴﺘﻘﻞ ﺧﻄی ﺍﻧﺪ. ﺑﺎ ﺷﺮﻁ 68

ﺗﺬکﺮ: ﻧﺘﺎیﺞ ﺑﺎﻻ ﺭﺍ ﺑﺮﺍی ﻣﻌﺎﺩﻻﺕ ﺩیﻔﺮﺍﻧﺴیﻞ ﺑﺎ ﺿﺮﺍیﺐ ﺛﺎﺑﺖ ﻣﺮﺗﺒﻪ ﺑﺎﻻﻧیﺰﻣی ﺗﻮﺍﻥ ﺗﻌﻤیﻢ کﺮﺩ. یﻌﻨی ﺍگﺮ ﻣﻌﺎﺩﻟﻪ کﻤکی ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺩﺍﺭﺍی ﺭیﺸﻪ ﻫﺎی ﺣﻘیﻘی ﻣﺘﻤﺎیﺰ ﻭﻣﻀﺎﻋﻒ ﻭﻣﺨﺘﻠﻂ ﺩﺍﺷﺘﻪ ﺑﺎﺷﺪ. آﻦ گﺎﻩ ﺟﻮﺍﺏ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺗﺮکیﺒی ﺍﺯ ﺟﻮﺍﺏ ﻫﺎی ﺑیﺎﻥ ﺷﺪﻩ ﺍﺳﺖ. 78

ﻣﺜﺎﻝ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺩﺍﺭﺍی ﻣﻌﺎﺩﻟﻪ کﻤکی ﻣی ﺑﺎﺷﺪ کﻪ ﺭیﺸﻪ ﻫﺎی آﻦ ﻋﺒﺎﺭﺕ ﺍﺳﺖ ﺍﺯ: ﺑﻨﺎﺑﺮﺍیﻦ ﺟﻮﺍﺏ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺍﺳﺖ. 88

ﻣﻌﺎﺩﻟﻪ کﺸی-ﺍﻭیﻠﺮ ﻣﻌﺎﺩﻟﻪ ﻣﺮﺗﺒﻪ ﺩﻭﻡ ﺧﻄی ﻫﻤگﻦ ﺍﻋﺪﺍﺩ ﺛﺎ ﺑﺖ ﺍﻧﺪ ﻣﻌﺎﺩﻟﻪ کﺸی- ﺭﺍکﻪ ﺩﺭآﻦ ﺍﻭیﻠﺮ) (Cauchy-Euler ﻣی ﻧﺎﻣیﻢ. ﻣﺜﺎﻝ ﻣﻌﺎﺩﻻﺕ ﺩیﻔﺮﺍﻧﺴیﻞ ﺯیﺮ ﻣﻌﺎﺩﻟﻪ ﻫﺎی کﺸی – ﺍﻭیﻠﺮ ﻣی ﺑﺎﺷﻨﺪ. ﺍﻟﻒ( ﺏ( 98

ﺣﻞ ﻣﻌﺎﺩﻟﻪ کﺸی – ﺍﻭیﻠﺮ ﻣی ﺗﻮﺍﻥ ﺑﻪ ﺍیﻦ ﻣﻌﺎﺩﻟﻪ ﺭﺍ ﺑﺎ ﺗﻐییﺮ ﻣﺘﻐیﺮ ﻣﻌﺎﺩﻟﻪ ﻣﺮﺗﺒﻪ ﺩﻭﻡ ﺑﺎ ﺿﺮیﺐ ﺛﺎﺑﺖ ﺗﺒﺪیﻞ کﺮﺩ ﺯیﺮﺍ : ﻭ ﻧﺸﺎﻥ ﻧﺴﺒﺖ ﺑﻪ ﺭﺍ ﺑﺎ ﺍگﺮ ﻣﺸﺘﻖ ﻫﺎی ﺩﻫیﻢ، ﻣﻌﺎﺩﻟﻪ ﺗﺒﺪیﻞ ﺑﻪ ﻣی ﺷﻮﺩ کﻪ ﻣﻌﺎﺩﻟﻪ ﺑﺎ ﺿﺮﺍیﺐ ﺛﺎﺑﺖ ﺍﺳﺖ. 09

ﻣﺜﺎﻝ: ﻣﻌﺎﺩﻟﻪ کﺸی – ﺍﻭیﻠﺮ ﺯیﺮ ﺭﺍ ﺣﻞ ﻣی کﻨیﻢ: ﺩﺍﺭیﻢ: ﺣﻞ: ﺑﺎ ﻓﺮﺽ ﺍﺳﺖ پﺲ ﻣﻌﺎﺩﻟﻪ کﻤکی ﺩﺍﺭﺍی ﺭیﺸﻪ ﻫﺎی ﺑﻨﺎﺑﺮﺍیﻦ: ( ﻧﺘیﺠﻪ ﻣی )یﺎ ﺑﺎ ﺟﺎیگﺬﺍﺭی ﺷﻮﺩ: 19ﺟﻮﺍﺏ ﻣﻌﺎﺩﻟﻪ کﺸی – ﺍﻭیﻠﺮ ﺍﺳﺖ.

ﺗﺬکﺮ : ﻧﺘﺎیﺞ ﺑﺎﻻ ﺭﺍ ﺑﺮﺍی ﻣﻌﺎﺩﻻﺕ ﺩیﻔﺮﺍﻧﺴیﻞ کﺸی – ﺍﻭیﻠﺮ ﻣﺮﺗﺒﻪ ﺑﺎﻻ ﻧیﺰ ﻣی ﺗﻮﺍﻥ ﺗﻌﻤیﻢ ﺩﺍﺩ. ﻣﺜﻼ ﻣﻌﺎﺩﻟﻪ کﺸی – ﺍﻭیﻠﺮ ﻣﺮﺗﺒﻪ ﺳﻮﻡ ﺗﺒﺪیﻞ ﺑﻪ ﻣﻌﺎﺩﻟﻪ : ﺭﺍ ﻣی ﺗﻮﺍﻥ ﺑﺎ ﺗﻐییﺮ ﻣﺘﻐیﺮ ﻧﻤﻮﺩ ﻭآﻨﺮﺍ ﺑﺎ ﺭﻭﺵ ﺿﺮﺍیﺐ ﺛﺎﺑﺖ ﺣﻞ کﺮﺩ. 29

ﻣﺜﺎﻝ : ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ کﺸی – ﺍﻭیﻠﺮ ﺯیﺮ ﺭﺍ ﺣﻞ ﻣی کﻨیﻢ: ﺩﺍﺭیﻢ : ﺣﻞ: ﺑﺎ ﻓﺮﺽ ﺑﻨﺎﺑﺮﺍیﻦ : 39

ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻣﺮﺗﺒﻪ ﺩﻭﻡ ﺧﻄی ﻏیﺮ ﻫﻤگﻦ ﻣﻼﺣﻈﻪ ﺷﺪ کﻪ ﻣﻌﺎﺩﻟﻪ ﻣﺮﺗﺒﻪ ﺩﻭﻡ ﺧﻄی ﺑﺎ ﺿﺮﺍیﺐ ﺛﺎﺑﺖ ﻣی ﻏیﺮ ﻫﻤگﻦ ﺑﺼﻮﺭﺕ آﻨﺮﺍ ﻣﻌﺎﺩﻟﻪ ﻣﺮﺗﺒﻪ ﺩﻭﻡ ﺧﻄی ﺑﺎ ﺑﺎﺷﺪ کﻪ ﺍگﺮ ﺿﺮﺍیﺐ ﺛﺎﺑﺖ ﻫﻤگﻦ ﻧﺎﻣیﻢ یﻌﻨی : ﻣی ﻭﺩﺍﺭﺍی ﺟﻮﺍﺑی ﺑﺼﻮﺭﺕ ﺑﺎﺷﺪ. 49

ﺟﻮﺍﺏ ﻋﻤﻮﻣی ﻣﻌﺎﺩﻟﻪ ﻫﻤگﻦ ﺣﺎﻝ ﺍگﺮ ﺟﻮﺍﺑی ﺧﺎﺹ ﺍﺯ ﻣﻌﺎﺩﻟﻪ ﻏیﺮ ﻫﻤگﻦ ﻭ ﺑﺎﺷﺪ آﻦ گﺎﻩ ﺟﻮﺍﺏ ﻋﻤﻮﻣی ﻣﻌﺎﺩﻟﻪ ﻏیﺮ ﻫﻤگﻦ ﻣی ﺑﺎﺷﺪ. 59

ﺭﺍ ﺗﻌﺮیﻒ : ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﺑﺎ ﺿﺮﺍیﺐ ﺛﺎﺑﺖ ﻭﺍﺑﺴﺘﻪ ﻣﻌﺎﺩﻟﻪ ﺩیﻔﺮﺍﻧﺴیﻞ ﻧﺎﻣیﻢ. ﻫﺪﻑ ﺍﺯ ﺍیﻦ ﻗﺴﻤﺖ ﺩﺭﺱ پیﺪﺍ کﺮﺩﻥ ﺟﻮﺍﺏ ﺧﺎﺹ ﻣﻌﺎﺩﻟﻪ ﻏیﺮ ﻫﻤگﻦ ﺍﺭﺍﺋﻪ ﻣی ﺑﺎﺷﺪ کﻪ ﺩﻭ ﺭﻭﺵ ﺑﺮﺍی پیﺪﺍ کﺮﺩﻥ ﺩﻫیﻢ. 69

ﺍﻟﻒ(ﺭﻭﺵ ﺗﻐییﺮ پﺎﺭﺍﻣﺘﺮ : ﺩﺭﺍیﻦ ﺭﻭﺵ ﻓﺮﺽ ﻣی کﻨیﻢ کﻪ ﺟﻮﺍﺏ ﺧﺎﺹ ﺑﺼﻮﺭﺕ ﺟﻮﺍﺏ ﻫﻤگﻦ ﺑﺎ ﺷﺪ کﻪ چﻮﻥ ﺑﻪ ﺗﻮﺍﺑﻊ ﻣی ﺑﺎﺷﺪ ﻭﺑﺎ ﺗﻐییﺮ پﺎﺭﺍﻣﺘﺮﻫﺎی ﺑﺪﺳﺖ آﻤﺪﻩ ﺍﺳﺖ، ﺑﻪ ﻫﻤیﻦ ﺩﻟیﻞ ﺍیﻦ ﻭ ﺭﻭﺵ ﺭﺍ ﺗﻐییﺮ پﺎﺭﺍﻣﺘﺮ ﻧﺎﻣیﻢ. 79

ﺣﺎﻝ ﺑﺎ ﺗﻮﺟﻪ ﺑﻪ ﻣﻌﻠﻮﻡ ﺑﻮﺩﻥ ﻇﺎﻫﺮ ﺟﻮﺍﺏ ﺧﺎﺹ کﺎﻓی ﺍﺳﺖ ﺩﺭآﻦ ﺻﺪﻕ ﻣی کﻨﻨﺪ ﺭﺍ پیﺪﺍ ﺭﻭﺍﺑﻄی کﻪ ﺗﻮﺍﺑﻊ کﻨیﻢ. ﺑﻨﺎﺑﺮﺍیﻦ ﺩﺍﺭیﻢ: ﺻﺪﻕ چﻮﻥ ﺑﺎیﺪ ﺩﺭﻣﻌﺎﺩﻟﻪ ﻫﻤگﻦ کﻨﺪ، ﺑﻨﺎﺑﺮﺍیﻦ 89

کﻪ ﺩﺳﺘگﺎﻩ ﺩﻭ ﻣﻌﺎﺩﻟﻪ ﺩﻭ ﻣﺠﻬﻮﻟی ﻣی ﺑﺎﺷﺪ ﻭﻣی ﺗﻮﺍﻥ ﺭﺍ ﻣﺤﺎﺳﺒﻪ کﺮﺩﻩ ﻭ ﺑﺎ ﺍﻧﺘگﺮﺍﻝ ﺍﺯ آﻦ ﻣﻘﺎﺩیﺮ گیﺮی ﻣﺤﺎﺳﺒﻪ ﻣی ﺷﻮﺩ ﻭﺍﺯ آﻦ ﺟﺎ ﺑﺪﺳﺖ ﻣی آیﺪ. ﺑﺎ یک ﻣﺜﺎﻝ ﺗﻮﺿیﺢ ﻣی ﺩﻫیﻢ 99

ﺭﺍ ﻣﺜﺎﻝ : ﻣﻌﺎﺩﻟﻪ ﻏیﺮ ﻫﻤگﻦ ﺣﻞ ﻣی کﻨیﻢ: ﺩﺍﺭﺍی ﺟﻮﺍﺏ ﺣﻞ : ﻣﻌﺎﺩﻟﻪ ﻭﺍﺑﺴﺘﻪ پﺲ: ﻭ ﺍﺳﺖ ﺑﻨﺎﺑﺮﺍیﻦ ﻭ ﺟﻤﻊ ﻃﺮﻓیﻦ ﺩﻭﻣﻌﺎﺩﻟﻪ ﺑﺎﻻ ﺑﺎ ﺿﺮﺏ ﻣﻌﺎﺩﻟﻪ ﺍﻭﻝ ﺩﺭ ﺩﺍﺭیﻢ: ﺩﺭﻣﻌﺎﺩﻟﻪ ﺍﻭﻝ ﺩﺍﺭیﻢ: ﺑﺎ ﺟﺎیگﺬﺍﺭی 001
ЛИТ.П. Ардебили Дж. - Диф. уравнения (химия).ppt