암호 시스템 CRYPTO SYSTEM 200310110 신효철 암호학

Зарегистрируйтесь, чтобы просмотреть полный документ!

암호 시스템 (CRYPTO SYSTEM) 200310110 신효철

암호학 기밀성과 인증을 해결하기 위한 수학적 연구 기밀성(Privacy) ○ 공개된 채널을 통해 정보의 누출 없이 문서를 안전하게 상대방에 게 전달 ○ 대칭키 알고리즘을 주로 이용 인증(Authentication) ○ 신분확인, 전자서명, 메시지 인증 등 ○ 공개키(비대칭키)알고리즘을 주로 이용

대칭키 알고리즘 가정 통신하려는 A, B는 공개되지 않은 같은키 공유 암호문을 만드는 알고리즘은 공개 암호문은 공개 목표 키를 모르고 공개된 알고리즘과 암호문 만으로는 평문 을 알 수가 없음 문제점 어떻게 서로 같은 키를 공유할 것인가? ○ 비공개 채널로 전송 ○ 공개키 알고리즘, 공개 키 분배 알고리즘

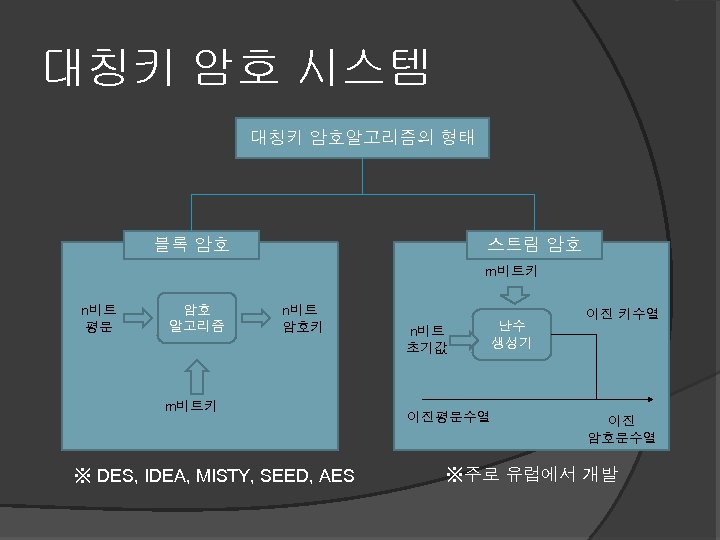
대칭키 암호 시스템 대칭키 암호알고리즘의 형태 블록 암호 스트림 암호 m비트키 n비트 평문 암호 알고리즘 n비트 암호키 m비트키 ※ DES, IDEA, MISTY, SEED, AES n비트 초기값 이진평문수열 난수 생성기 이진 키수열 이진 암호문수열 ※주로 유럽에서 개발

공개키 알고리즘 가정 키 Ex 와 Dx 를 직접 만들어서 Dx 는 감추고 Ex 는 공개 함 암호알고리즘과 암호문이 공개 목표 Ex 암호 알고리즘과 암호문으로 평문을 알 수가 없음 문제점 안전을 위해서는 키 길이가 길고 암호문 작성 시간도 비 밀키에 비해 100 – 1000배 정도 느림 장점 키 분배용으로 사용 할 수 있음 인증등에 적합

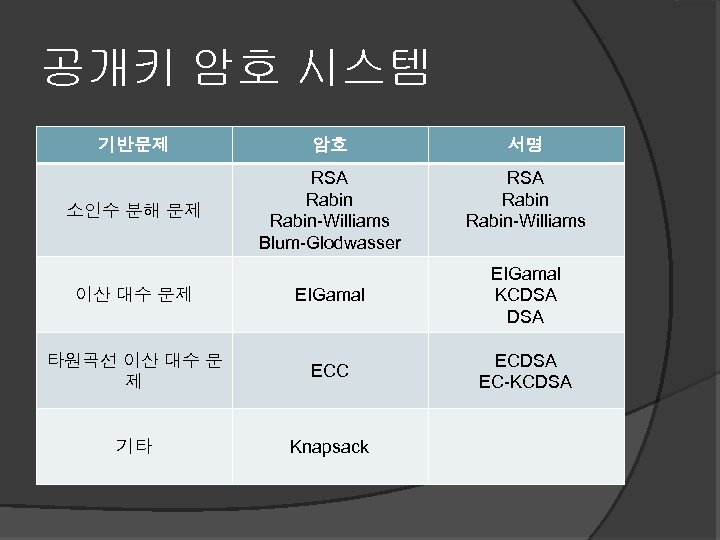
공개키 암호 시스템 기반문제 암호 서명 소인수 분해 문제 RSA Rabin-Williams Blum-Glodwasser RSA Rabin-Williams 이산 대수 문제 EIGamal KCDSA 타원곡선 이산 대수 문 제 ECC ECDSA EC-KCDSA 기타 Knapsack

공개키 종류 RSA(Rivest Shamir Adleman) 공개키와 개인키를 세트로 만들어서 암호화와 복호 화를 하는 인터넷 암호화 및 인증 시스템 ○ (암호화)공개키 (복호화)개인키 특정한 상대만 가능한 복호화, 특정상대에게 메세지전달 ○ (암호화)개인키 (복호화)공개키 상대방에게 자신임을 증명. Ex) 전자서명 두 소수를 가지고 비밀키, 암호키를 생성 ○ 공개키 두 소수의 곱으로 생성 ○ 비밀키 두 소수의 곱을 소인수분해 해서 생성 두 소수의 크기가 클수록 보안성이 커짐 두 소수의 크기가 커질수록 복호화 시간도 늘어남

공개키 종류 ECC(Elliptic Curve Cryptosystem) 타원곡선 시스템을 이용한 공개키 암호방식 짧은 키 사이즈로 높은 안전성 서명할 때의 계산을 고속 스마트카드(IC카드) 등의 정보처리능력이 그다지 높지 않은 기기에서 이용하기에 적합한 암호화 방식

공개키종류 KCDSA(Korea Certification-based Digital Signature Algori ) 이산대수 문제의 어려움에 기반을 둔 전자서명 알고리즘 한국통신정보보호학회의 주관 하에 우리 나라의 주요 암호 학자들이 주축이 되어 1996년 11월에 개발 ECKCDSA(Certificate-based Digital Signature Algorithm using Elliptic Curves) KCDSA 전자서명을 타원곡선을 이용한 전자서명 알고리즘 으로 변형한 것 공개키 시스템의 키 길이에 비해서 훨씬 짧은 키를 사용하 여도 동일한 안전도를 제공하므로 스마트 카드, 무선 통신 등과 같이 메모리와 처리능력이 제한된 분야에서 매우 효 과

대칭키 vs 공개키 암호시스템 항목 ＼ 암호시스템 대칭키 공개키 키의 상호관계 암호화키 = 복호화키 암호화키 ≠ 복호화키 암호화키 비밀 공개 복호화키 비밀 비밀 암호알고리즘 비밀/공개 공개 대표적인예 DES, IDEA, SEED RSA, EIGamal, ECC 비밀키 전송 필요 불필요 키의 개수 n(n-1)/2 2 n 안전한 인증 곤란 용이 암호화 속도 고속 저속 경제성 高低 전자서명 복잡 간단

Скачать презентацию 암호 시스템 CRYPTO SYSTEM 200310110 신효철 암호학

224ea6a6f66e9fca7c1437b37e342786.ppt

Количество слайдов: 10