dc5154523c2907b01895280bc11eac71.ppt
- Количество слайдов: 105

第 9章 晶体化学基础

主要内容 q q q 原子结构和周期表 原子和离子半径 密堆积原理 配位数和配位多面体 化学键和晶格类型

原子结构 q q q 原子是由运动着的粒子组成的复杂的微观体系 它由带正电的原子核和绕核运动的带负电的电 子(e)组成 原子核=质子(p) +中子(n) 粒子 质子 中子 电子 符号 p n e 质量(克) 1. 673× 10 -24 1. 675× 10 -24 9. 109× 10 -28 电荷量(静电单位) + 4. 803× 10 -10 0 - 4. 803× 10 -10
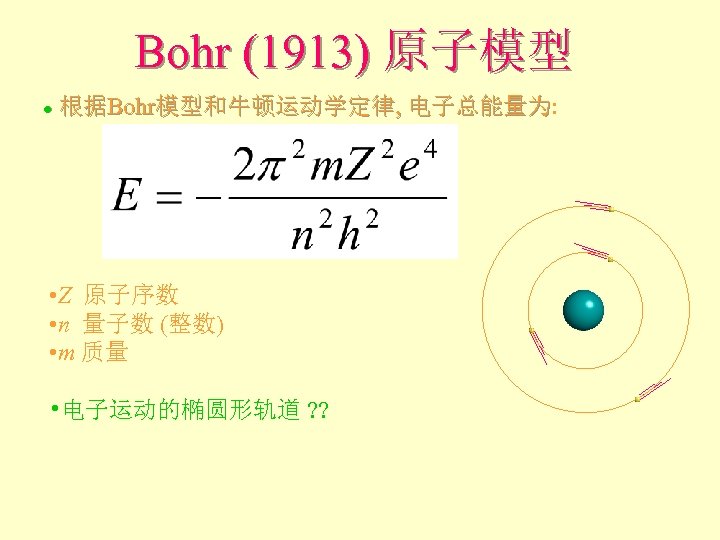
Bohr (1913) 原子模型 根据Bohr模型和牛顿运动学定律, 电子总能量为: 电子总能量为 l • Z 原子序数 • n 量子数 (整数) • m 质量 • 电子运动的椭圆形轨道 ? ?
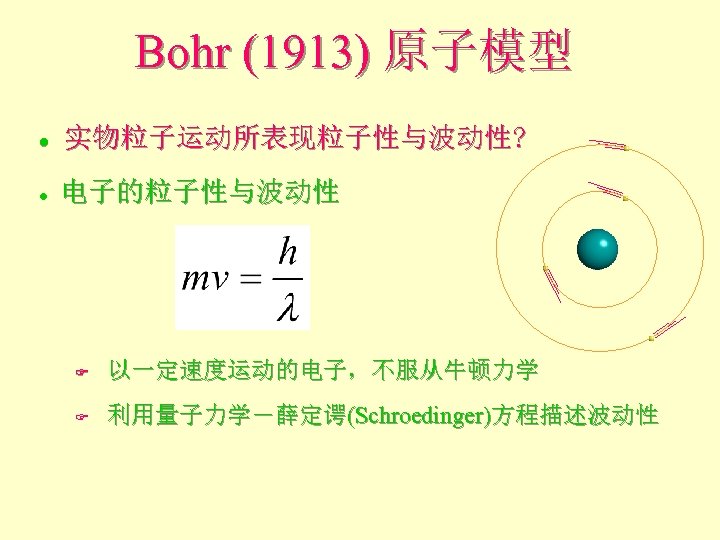
Bohr (1913) 原子模型 l 实物粒子运动所表现粒子性与波动性? l 电子的粒子性与波动性 F 以一定速度运动的电子,不服从牛顿力学 F 利用量子力学-薛定谔(Schroedinger)方程描述波动性

电子运动的波动性 F F 量子力学的假设运动的电子可用一个坐标函数Ψ(x, y, z), 即波函数来描述。此波函数没有明显的物理意义, 但波 函数的平方|Ψ(x, y, z, t)|2则 表示在某坐标处单 位体积 内找 到粒子的几率, 即电子在空间分布的几率密度与之成正 比 运动的电子,其波函数服从Schroedinger方程 x, y, z为坐标, m为电子质量, E为体系的总能量, V为电子的势能

量子数和轨道 主量子数 n (= 1, 2, 3, …) l F 决定体系能量,也表示电子运动时所占据的有效体积。通常用大写 字母K、L、M、N等主层符号来表示其轨道 角量子数 l (= 0, 1, 2…, (n-1)) l F 决定体系的角动量和电子云形状,同时也标志着轨道的分层数(亚 层轨道),一般用小写字母s、p、d、f等来表示 磁量子数 m (= 0, l, 2, 3, . . . , l) l F 决定电子云的方向和轨道角动量在磁场方向的分量 自旋量子数 s (= 1/2) 它主量子数 n (= 1, 2, 3, …) l F 标志着电子的自旋方向相反的运动状态

原子能级 l F 能级主要取决于主量子数n F 如果主量子数相同, 则轨道能级决定于角量子数l F 当n = 3以后,由于屏蔽效应,使得能量次序有颠倒的现象 核外电子在各个轨道排布遵循的规则 l F 能量最低原理 F 保利(Pouli)不相容原理 F 洪德(Hund)规则

原子能级 主层 电子数 亚层 (n = 1) 2 e s (n = 2) 8 e s, p M 外 层 K L 最内层 (n = 3) 18 e s, p, d N (n = 4) 32 e s, p, d, f (generally higher E)
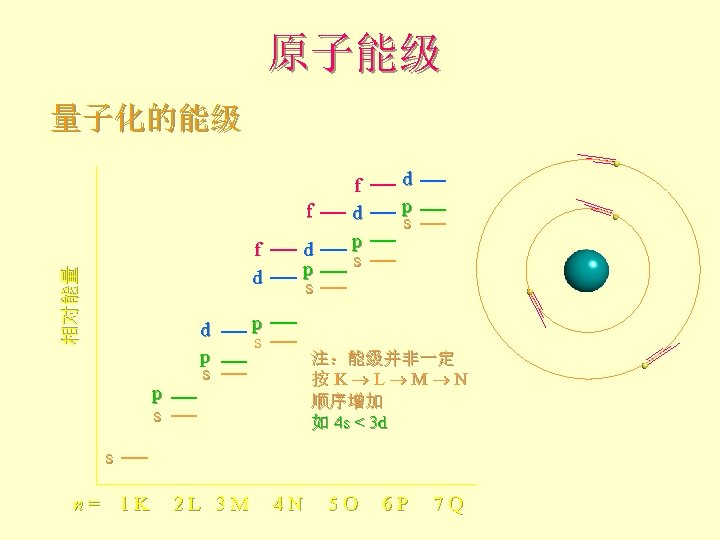
原子能级 量子化的能级 f 相对能量 f d p s p s d p s f d p s 注:能级并非一定 按 K L M N 顺序增加 如 4 s < 3 d s n = 1 K 2 L 3 M 4 N 5 O 6 P 7 Q
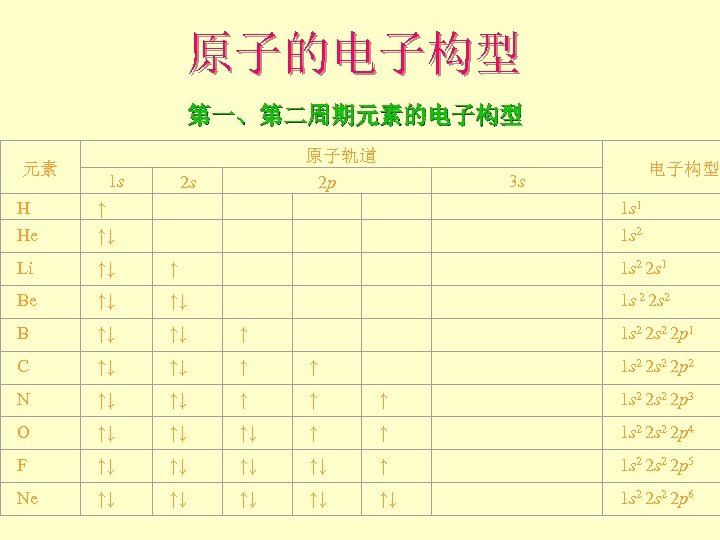
原子的电子构型 第一、第二周期元素的电子构型 H He ↑ ↑↓ 原子轨道 2 p Li ↑↓ ↑ 1 s 2 2 s 1 Be ↑↓ ↑↓ 1 s 2 2 s 2 B ↑↓ ↑↓ ↑ 1 s 2 2 p 1 C ↑↓ ↑↓ ↑ ↑ 1 s 2 2 p 2 N ↑↓ ↑↓ ↑ ↑ ↑ 1 s 2 2 p 3 O ↑↓ ↑↓ ↑↓ ↑ ↑ 1 s 2 2 p 4 F ↑↓ ↑↓ ↑ 1 s 2 2 p 5 Ne ↑↓ ↑↓ ↑↓ 1 s 2 2 p 6 元素 1 s 2 s 电子构型 3 s 1 s 1 1 s 2
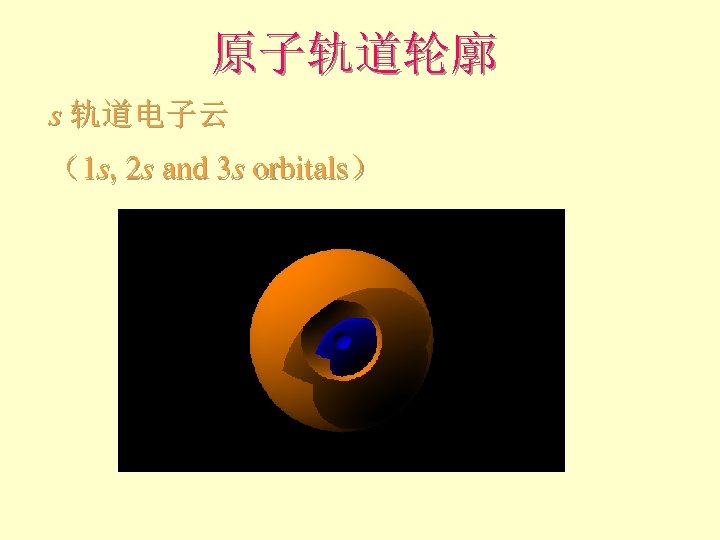
原子轨道轮廓 s 轨道电子云 (1 s, 2 s and 3 s orbitals)
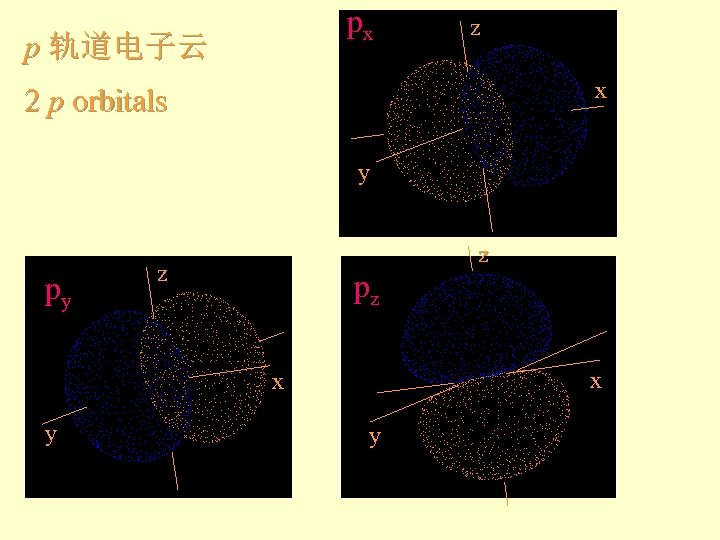
px p 轨道电子云 z x 2 p orbitals y py z z pz x x y y
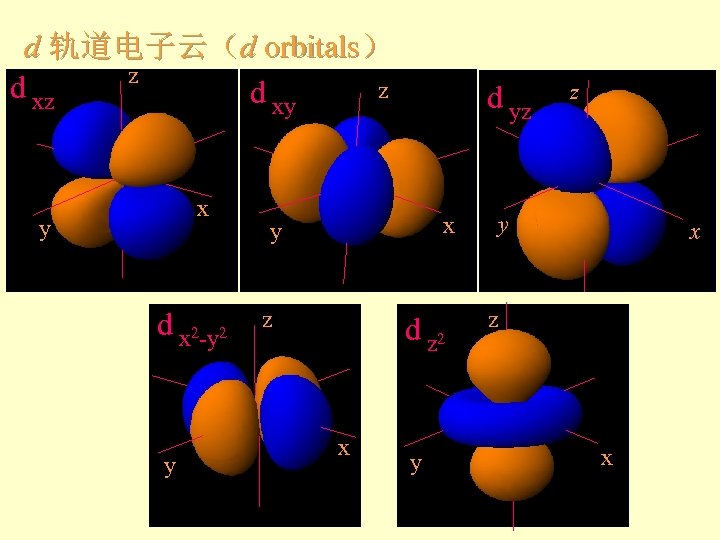
d 轨道电子云(d orbitals) z d xz z d xy x y d x 2 -y 2 y d yz x y z d z 2 x y z y x z x

The Periodic Table
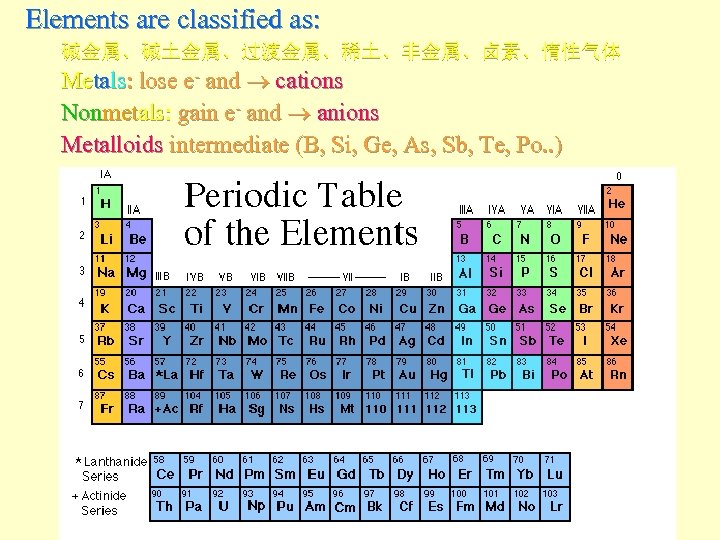
Elements are classified as: 碱金属、碱土金属、过渡金属、稀土、非金属、卤素、惰性气体 Metals: lose e- and cations Nonmetals: gain e- and anions Metalloids intermediate (B, Si, Ge, As, Sb, Te, Po. . )
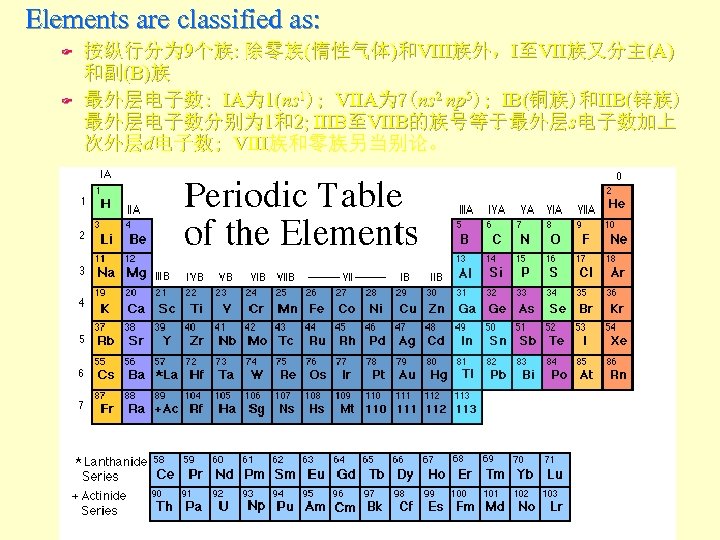
Elements are classified as: F F 按纵行分为 9个族: 除零族(惰性气体)和VIII族外,I至VII族又分主(A) 和副(B)族 最外层电子数: IA为 1(ns 1); VIIA为 7(ns 2 np 5); IB(铜族)和IIB(锌族) 最外层电子数分别为 1和2; IIIB至VIIB的族号等于最外层s电子数加上 次外层d电子数; VIII族和零族另当别论。

Atomic and Ionic Radii 原子和离子半径

Atomic and Ionic Radii l l 不能绝对测量(不可能确切知道e-的运动状况, 即运动 速度和位置) 如果将电子云的分布空间(体积)视为球形,则球的半 径就是原子或离子的半径 = 理论半径 以键长数据为基础,由实验方法得到的原子或离子半 径称为原子或离子的有效半径 对应于不同的化学键,也有离子半径、共价半径及金 属原子半径的区别
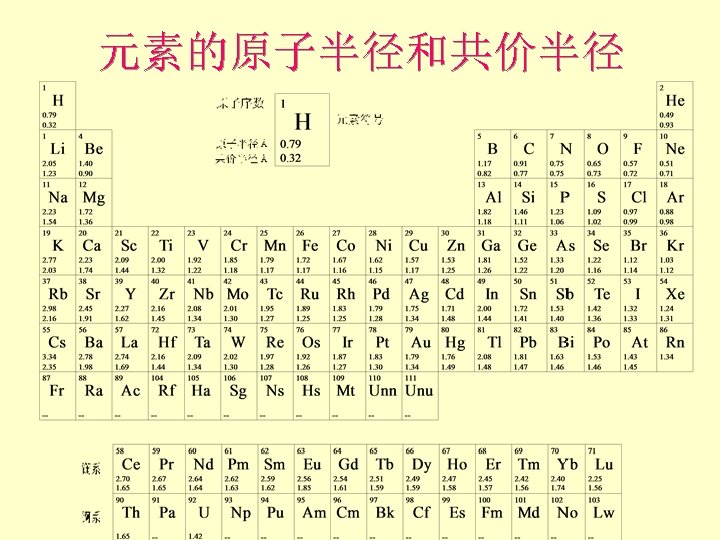
元素的原子半径和共价半径

Atomic and Ionic Radii 周期表中的规律: l 同种元素原子半径: 共价半径 < 金属原子半径 l 同种元素离子半径: rcation < ranion l 同族元素: 原子和离子半径随周期数增加而增大 l 同一周期元素: 原子和离子半径随Z的增加而减小 l 从周期表左上到右下对角线上,阳离子半径近于相等 l 镧系和锕系: 阳离子半径随Z增加而略有减小 l Generally, 阳离子半径都小于阴离子半径。阳离子半 径在 0. 5~ 1. 2 Å的范围内,而阴离子半径则在 1. 2~ 2. 2 Å之间
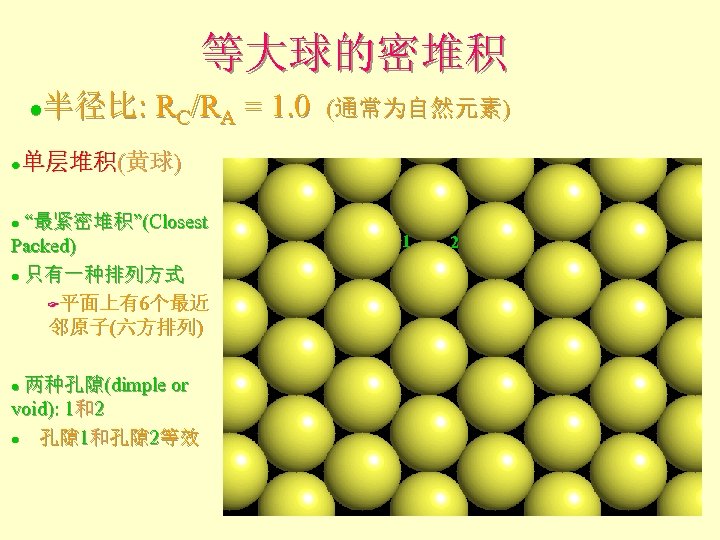
等大球的密堆积 半径比: RC/RA = 1. 0 (通常为自然元素) l 单层堆积(黄球) l “最紧密堆积”(Closest Packed) l 只有一种排列方式 F平面上有6个最近 邻原子(六方排列) l 两种孔隙(dimple or void): 1和2 l 孔隙 1和孔隙 2等效 l 1 2
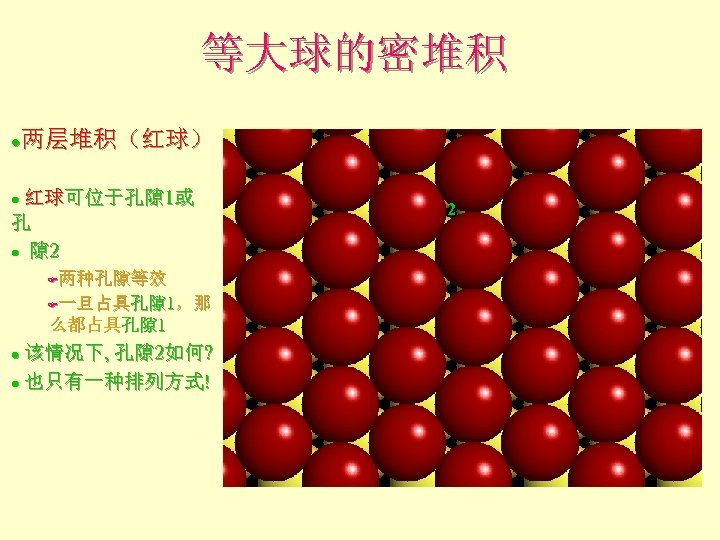
等大球的密堆积 两层堆积(红球) l 红球可位于孔隙 1或 孔 l 隙 2 l F两种孔隙等效 F一旦占具孔隙 1,那 么都占具孔隙 1 该情况下, 孔隙 2如何? l 也只有一种排列方式! l 2
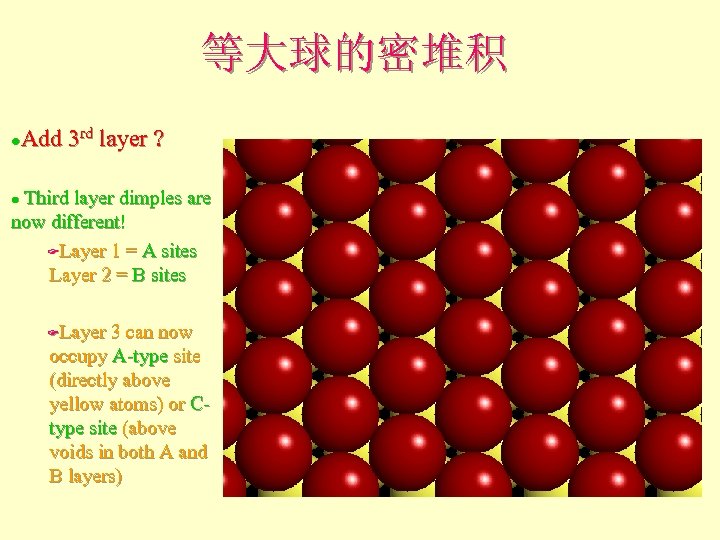
等大球的密堆积 Add 3 rd layer ? l Third layer dimples are now different! FLayer 1 = A sites Layer 2 = B sites l Layer 3 can now occupy A-type site (directly above yellow atoms) or Ctype site (above voids in both A and B layers) F

等大球的密堆积 Add 3 rd layer (yellow) l If occupy A-type site Fthe layer ordering becomes ABAB… and creates a hexagonal closest packed structure (hcp) l Coordination number (nearest or touching neighbors) = 12 F 6 coplanar F
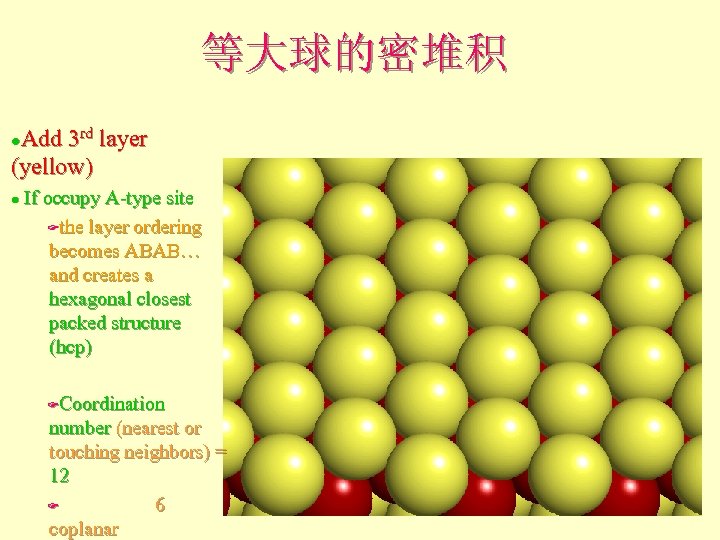
等大球的密堆积 Add 3 rd layer (yellow) l If occupy A-type site Fthe layer ordering becomes ABAB… and creates a hexagonal closest packed structure (hcp) l Coordination number (nearest or touching neighbors) = 12 F 6 coplanar F
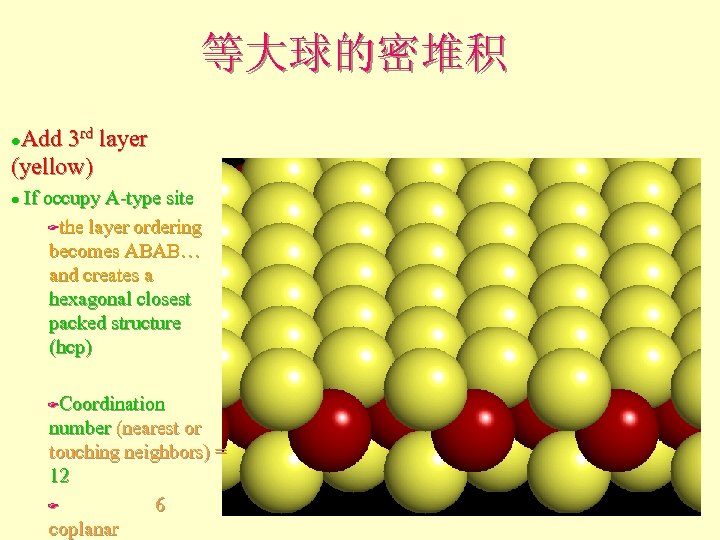
等大球的密堆积 Add 3 rd layer (yellow) l If occupy A-type site Fthe layer ordering becomes ABAB… and creates a hexagonal closest packed structure (hcp) l Coordination number (nearest or touching neighbors) = 12 F 6 coplanar F
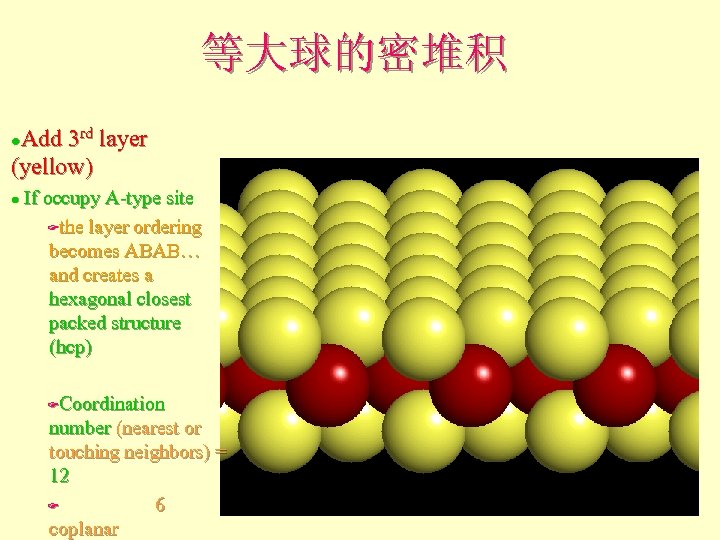
等大球的密堆积 Add 3 rd layer (yellow) l If occupy A-type site Fthe layer ordering becomes ABAB… and creates a hexagonal closest packed structure (hcp) l Coordination number (nearest or touching neighbors) = 12 F 6 coplanar F
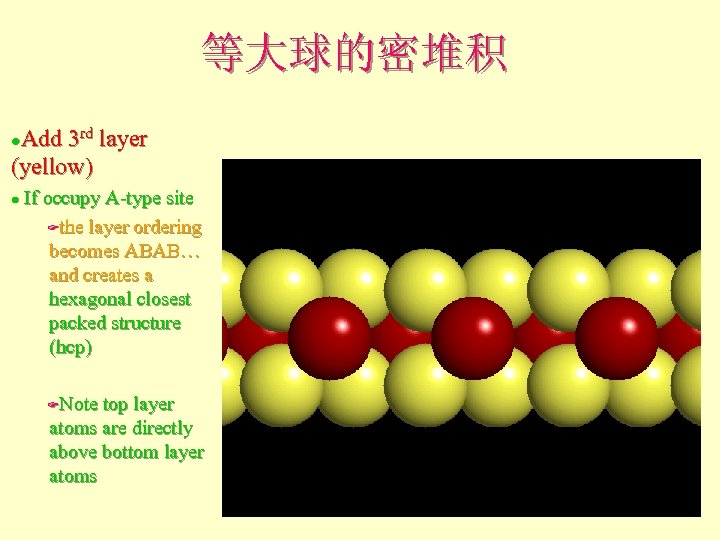
等大球的密堆积 Add 3 rd layer (yellow) l If occupy A-type site Fthe layer ordering becomes ABAB… and creates a hexagonal closest packed structure (hcp) l Note top layer atoms are directly above bottom layer atoms F
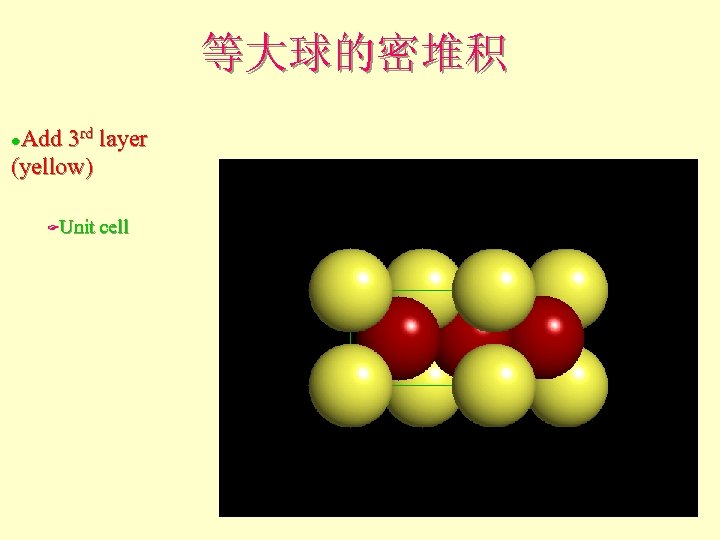
等大球的密堆积 Add 3 rd layer (yellow) l Unit cell F
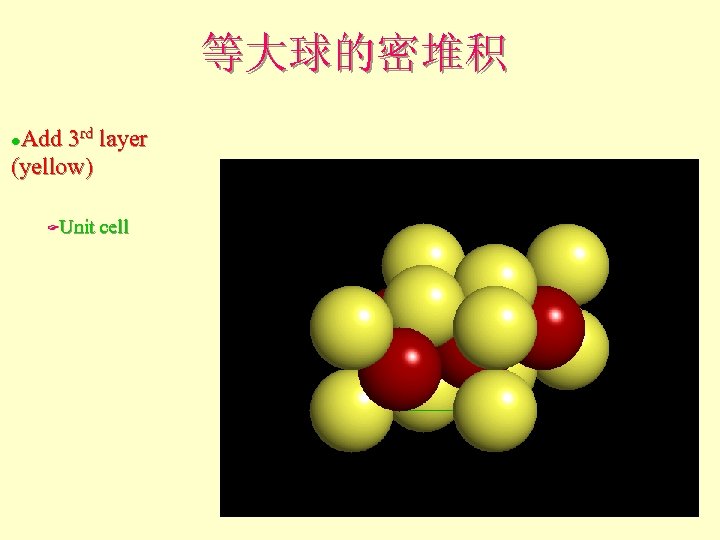
等大球的密堆积 Add 3 rd layer (yellow) l Unit cell F
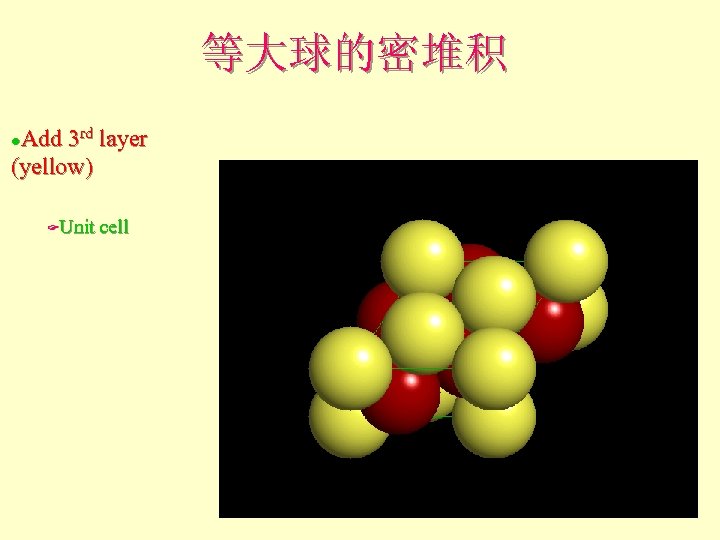
等大球的密堆积 Add 3 rd layer (yellow) l Unit cell F
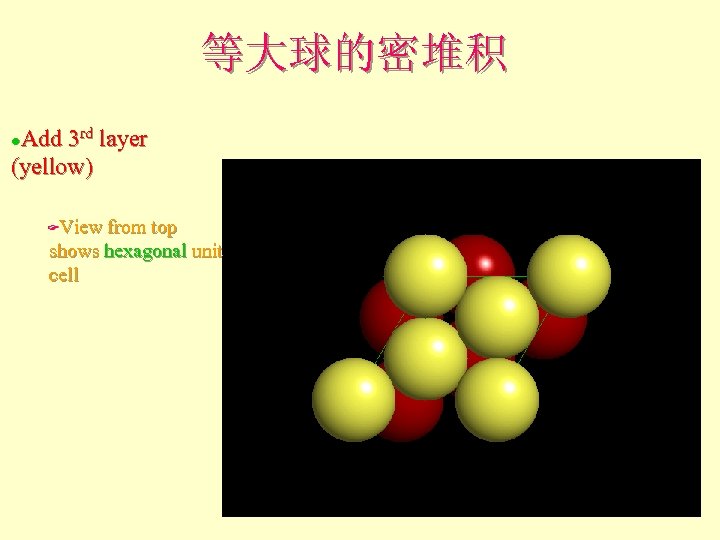
等大球的密堆积 Add 3 rd layer (yellow) l View from top shows hexagonal unit cell F
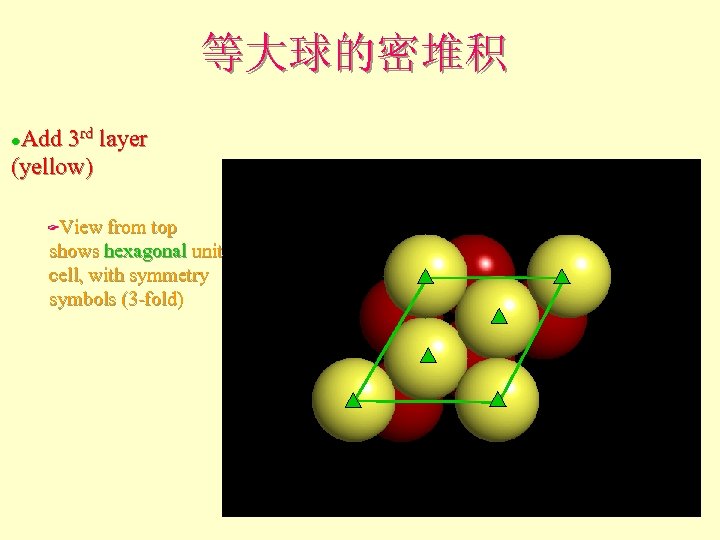
等大球的密堆积 Add 3 rd layer (yellow) l View from top shows hexagonal unit cell, with symmetry symbols (3 -fold) F

等大球的密堆积 Alternatively, we could place third layer in the C-type site (above voids in both A and B layers) l

等大球的密堆积 Third layer: F If occupy C-type site the layer ordering is ABCABC… and creates a cubic closest packed structure (ccp) F Blue layer atoms are now in a unique position above voids between atoms in layers A and B l
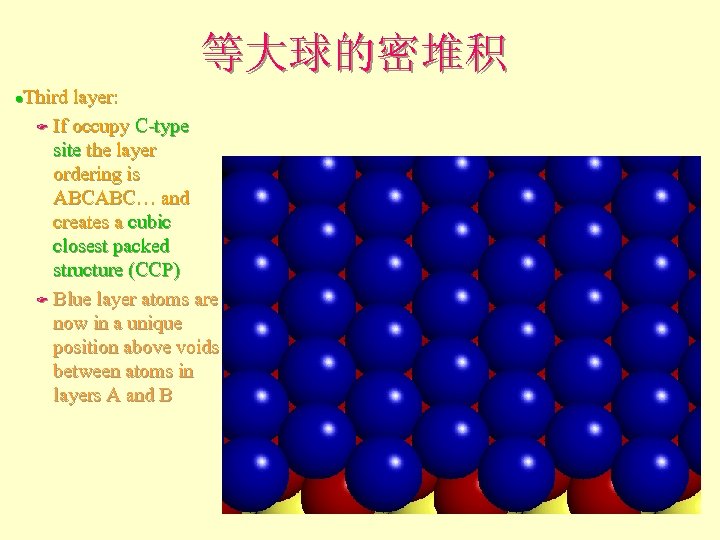
等大球的密堆积 Third layer: F If occupy C-type site the layer ordering is ABCABC… and creates a cubic closest packed structure (CCP) F Blue layer atoms are now in a unique position above voids between atoms in layers A and B l

等大球的密堆积 Third layer: F If occupy C-type site the layer ordering is ABCABC… and creates a cubic closest packed structure (CCP) F Blue layer atoms are now in a unique position above voids between atoms in layers A and B l

等大球的密堆积 Third layer: F If occupy C-type site the layer ordering is ABCABC… and creates a cubic closest packed structure (CCP) F Blue layer atoms are now in a unique position above voids between atoms in layers A and B l

等大球的密堆积 Third layer: F If occupy C-type site the layer ordering is ABCABC… and creates a cubic closest packed structure (CCP) F Blue layer atoms are now in a unique position above voids between atoms in layers A and B l
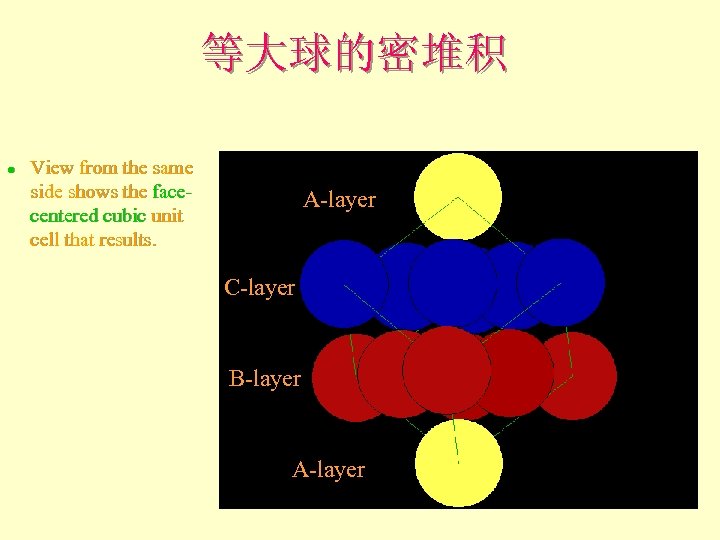
等大球的密堆积 l View from the same side shows the facecentered cubic unit cell that results. A-layer C-layer B-layer A-layer

等大球的密堆积 l Rotating toward a top view
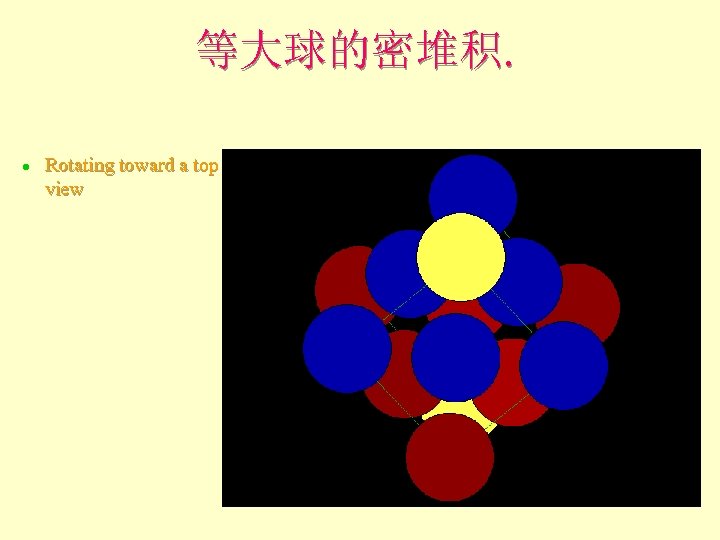
等大球的密堆积. l Rotating toward a top view

等大球的密堆积 l You are looking at a top yellow layer A with a blue layer C below, then a red layer B and a yellow layer A again at the bottom
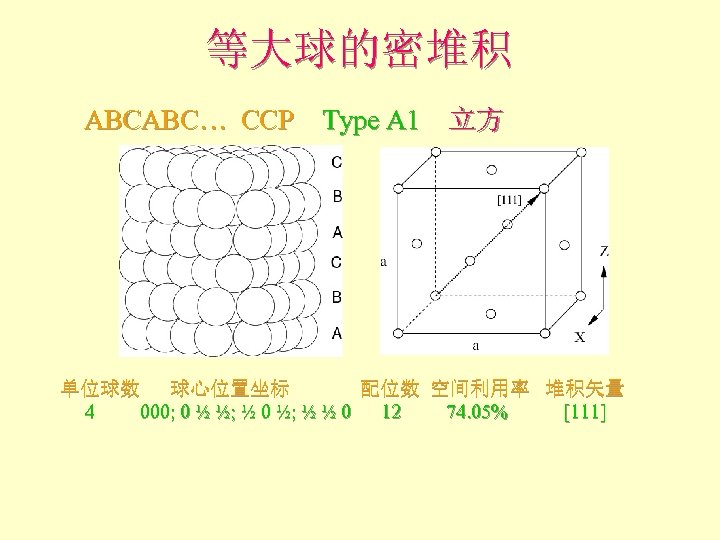
等大球的密堆积 ABCABC… CCP Type A 1 立方 单位球数 球心位置坐标 配位数 空间利用率 堆积矢量 4 000; 0 ½ ½; ½ 0 ½; ½ ½ 0 12 74. 05% [111]
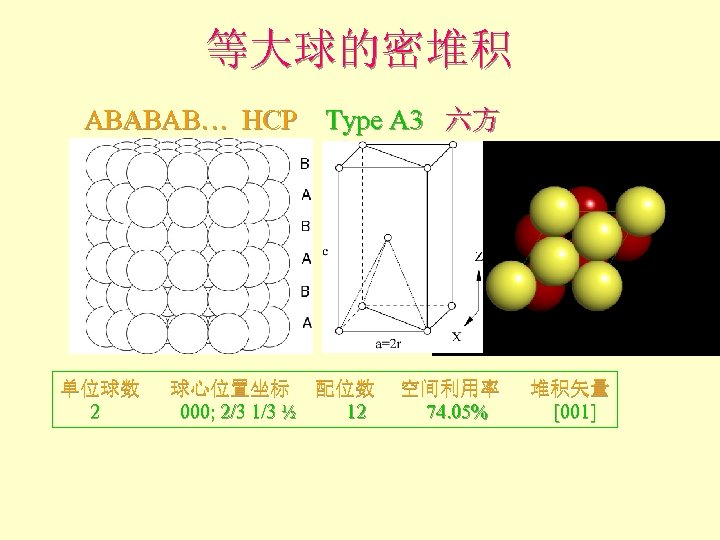
等大球的密堆积 ABABAB… HCP Type A 3 六方 单位球数 球心位置坐标 配位数 空间利用率 堆积矢量 2 000; 2/3 1/3 ½ 12 74. 05% [001]
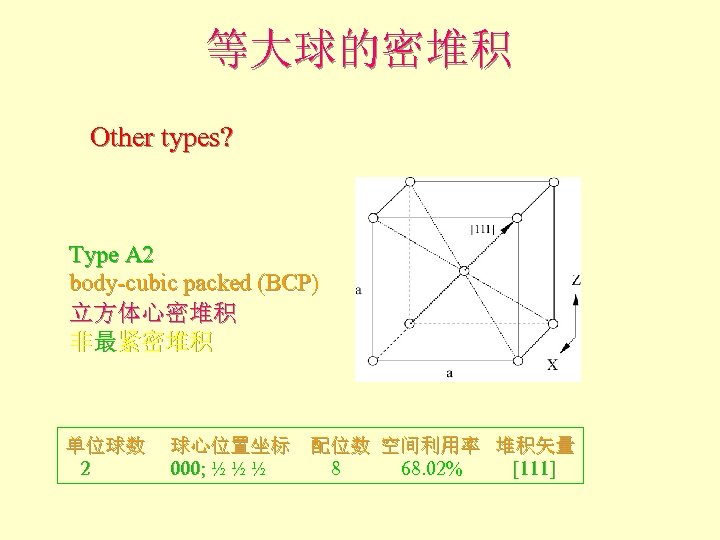
等大球的密堆积 Other types? Type A 2 body-cubic packed (BCP) 立方体心密堆积 非最紧密堆积 单位球数 球心位置坐标 配位数 空间利用率 堆积矢量 2 000; ½ ½ ½ 8 68. 02% [111]
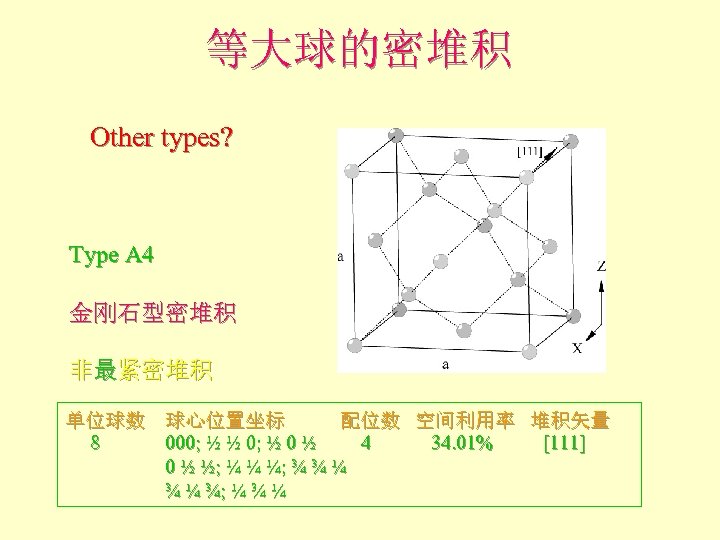
等大球的密堆积 Other types? Type A 4 金刚石型密堆积 非最紧密堆积 单位球数 球心位置坐标 配位数 空间利用率 堆积矢量 8 000; ½ ½ 0; ½ 0 ½ 4 34. 01% [111] 0 ½ ½; ¼ ¼ ¼; ¾ ¾ ¼ ¾ ¼ ¾; ¼ ¾ ¼
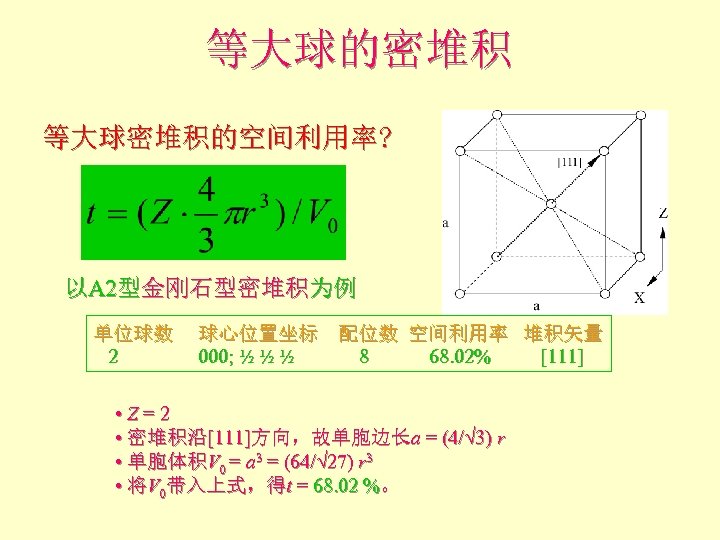
等大球的密堆积 等大球密堆积的空间利用率? 以A 2型金刚石型密堆积为例 单位球数 球心位置坐标 配位数 空间利用率 堆积矢量 2 000; ½ ½ ½ 8 68. 02% [111] • Z = 2 • 密堆积沿[111]方向,故单胞边长a = (4/√ 3) r • 单胞体积V 0 = a 3 = (64/√ 27) r 3 • 将V 0带入上式,得t = 68. 02 %。
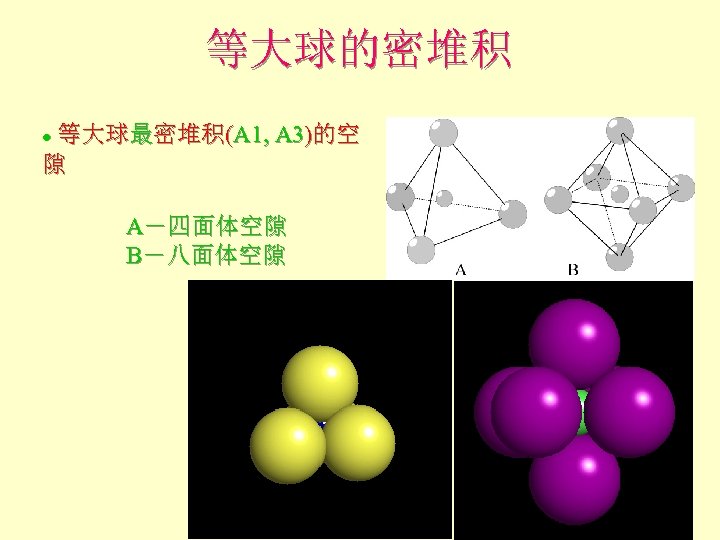
等大球的密堆积 等大球最密堆积(A 1, A 3)的空 隙 l A-四面体空隙 B-八面体空隙
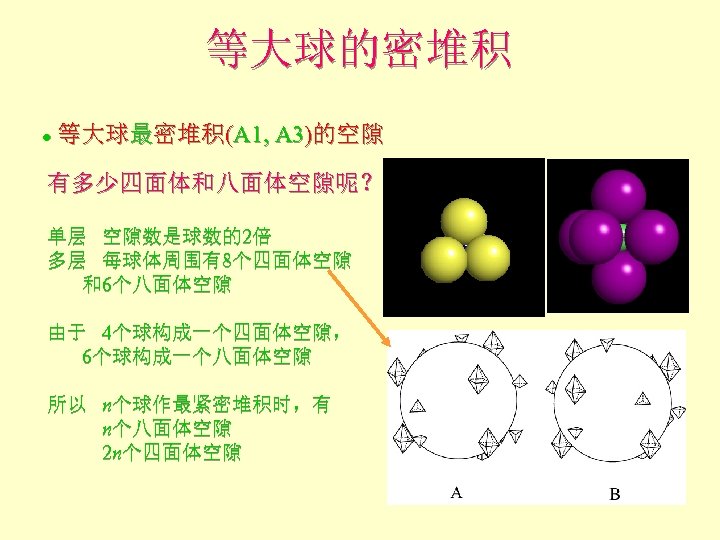
等大球的密堆积 等大球最密堆积(A 1, A 3)的空隙 l 有多少四面体和八面体空隙呢? 单层 空隙数是球数的2倍 多层 每球体周围有8个四面体空隙 和6个八面体空隙 由于 4个球构成一个四面体空隙, 6个球构成一个八面体空隙 所以 n个球作最紧密堆积时,有 n个八面体空隙 2 n个四面体空隙
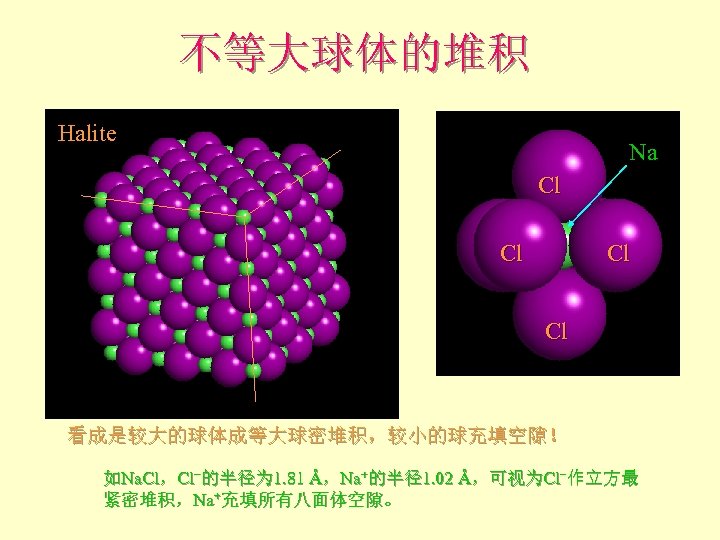
不等大球体的堆积 Halite Na Cl Cl 看成是较大的球体成等大球密堆积,较小的球充填空隙! 如Na. Cl,Cl−的半径为 1. 81 Å,Na+的半径1. 02 Å,可视为Cl−作立方最 紧密堆积,Na+充填所有八面体空隙。
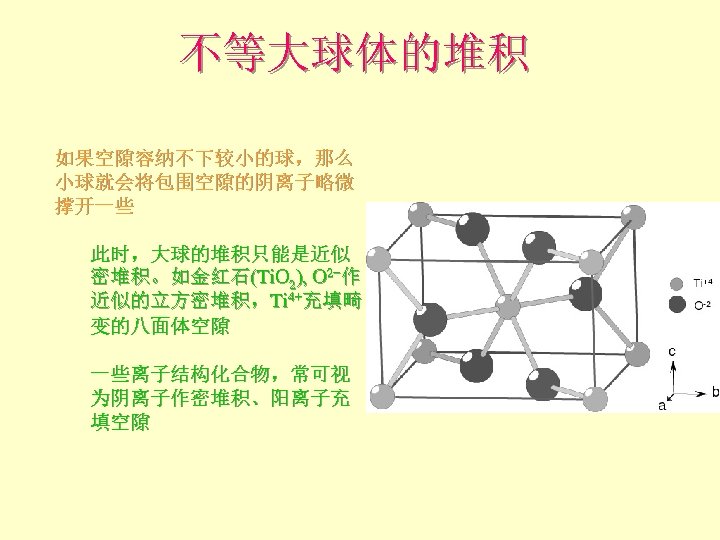
不等大球体的堆积 如果空隙容纳不下较小的球,那么 小球就会将包围空隙的阴离子略微 撑开一些 此时,大球的堆积只能是近似 密堆积。如金红石(Ti. O 2), O 2−作 近似的立方密堆积,Ti 4+充填畸 变的八面体空隙 一些离子结构化合物,常可视 为阴离子作密堆积、阳离子充 填空隙
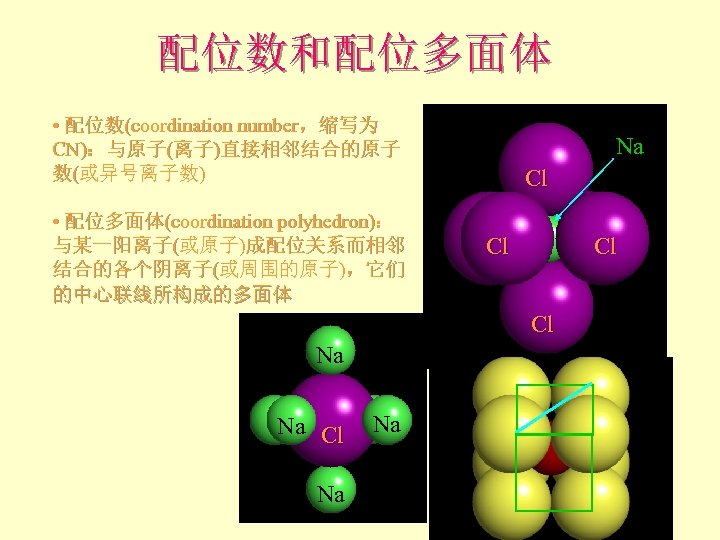
配位数和配位多面体 • 配位数(coordination number,缩写为 CN):与原子(离子)直接相邻结合的原子 数(或异号离子数) • 配位多面体(coordination polyhedron): 与某一阳离子(或原子)成配位关系而相邻 结合的各个阴离子(或周围的原子),它们 的中心联线所构成的多面体 Na Cl Cl Na Na

配位数和配位多面体 • 配位数和配位多面体由多种因素决定 化学键类型、质点相对大小、堆积的紧密程度… 金属键:最紧密堆积,CN = 12。如Cu,Au等,A 1型密堆积;非最 紧密堆积,CN要减低。如a-Fe,CN = 8, A 2型密堆积 共价键:共价键具方向性和饱和性,配位数取决于成键个数,不受 球体密堆积规律的支配。如金刚石中碳原子形成四个共价键,CN = 4;石墨中碳原子形成三个共价键,CN = 3
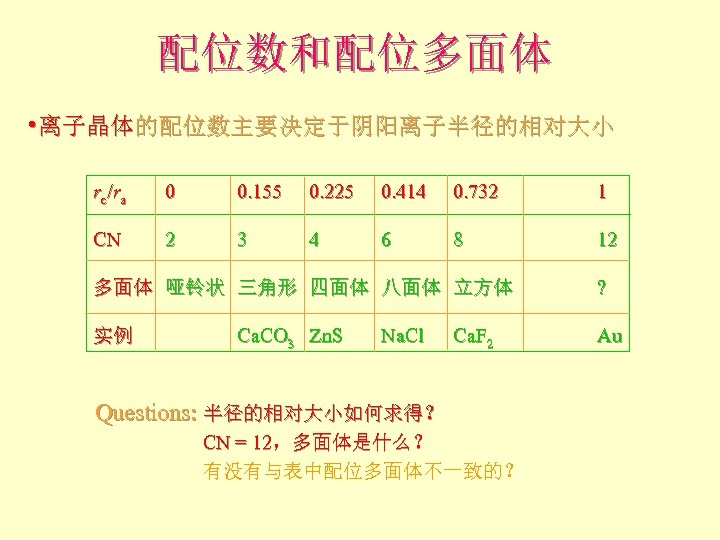
配位数和配位多面体 • 离子晶体的配位数主要决定于阴阳离子半径的相对大小 rc / ra 0 0. 155 0. 225 0. 414 0. 732 1 CN 2 3 4 6 8 12 多面体 哑铃状 三角形 四面体 八面体 立方体 实例 Ca. CO 3 Zn. S Na. Cl Ca. F 2 Questions: 半径的相对大小如何求得? CN = 12,多面体是什么? 有没有与表中配位多面体不一致的? ? Au
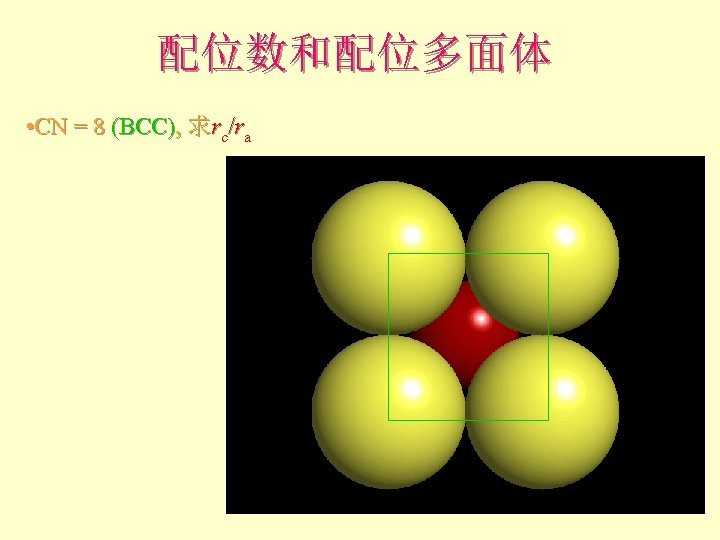
配位数和配位多面体 • CN = 8 (BCC), 求rc/ra
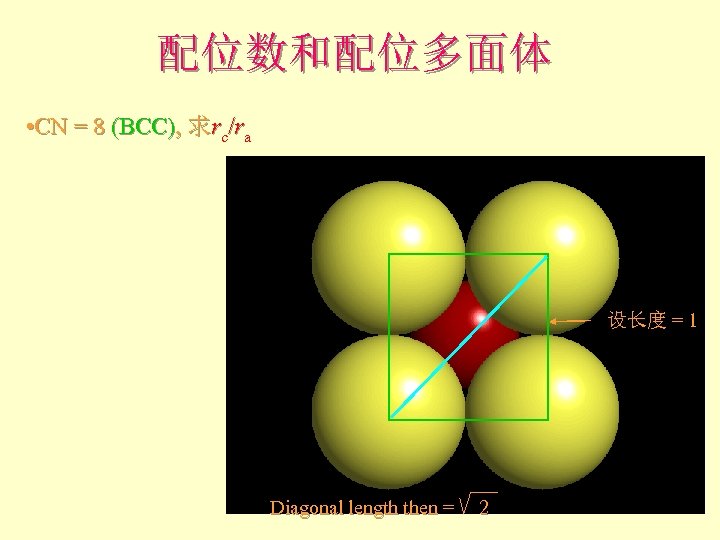
配位数和配位多面体 • CN = 8 (BCC), 求rc/ra 设长度 = 1 Diagonal length then = 2
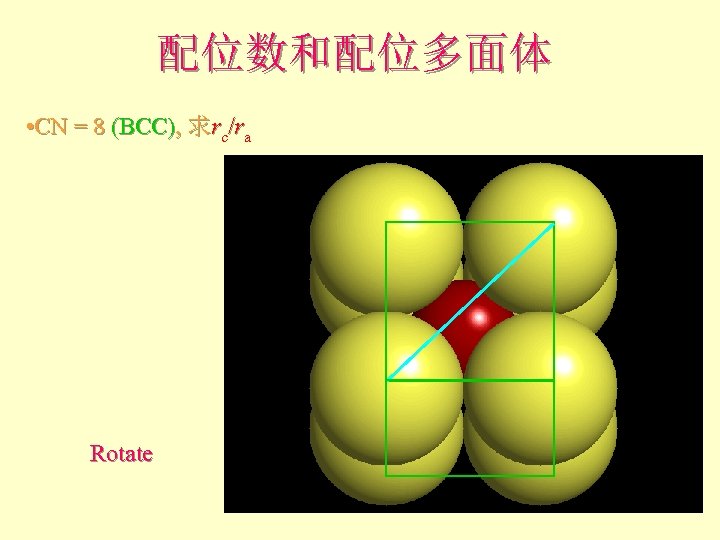
配位数和配位多面体 • CN = 8 (BCC), 求rc/ra Rotate
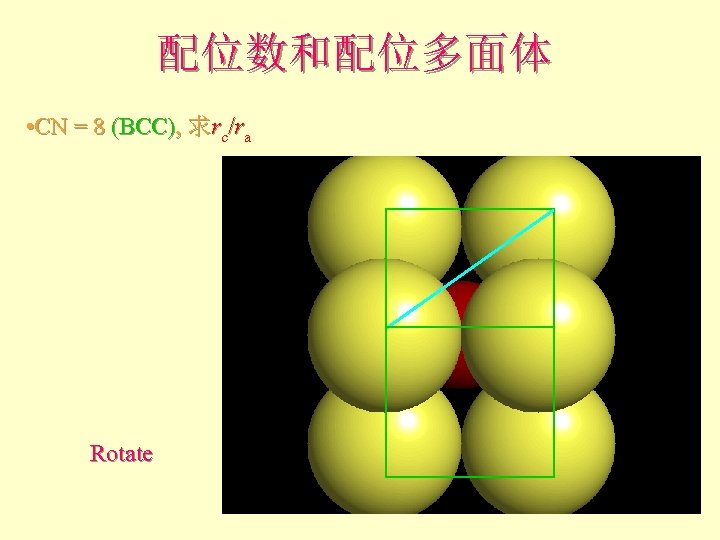
配位数和配位多面体 • CN = 8 (BCC), 求rc/ra Rotate
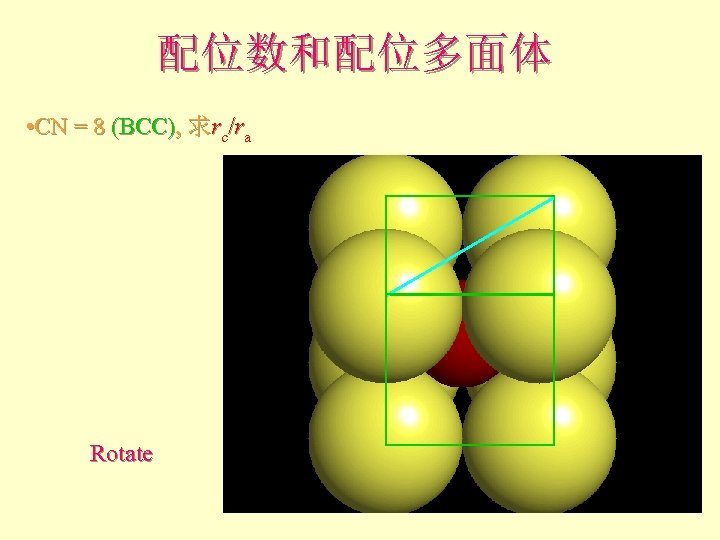
配位数和配位多面体 • CN = 8 (BCC), 求rc/ra Rotate
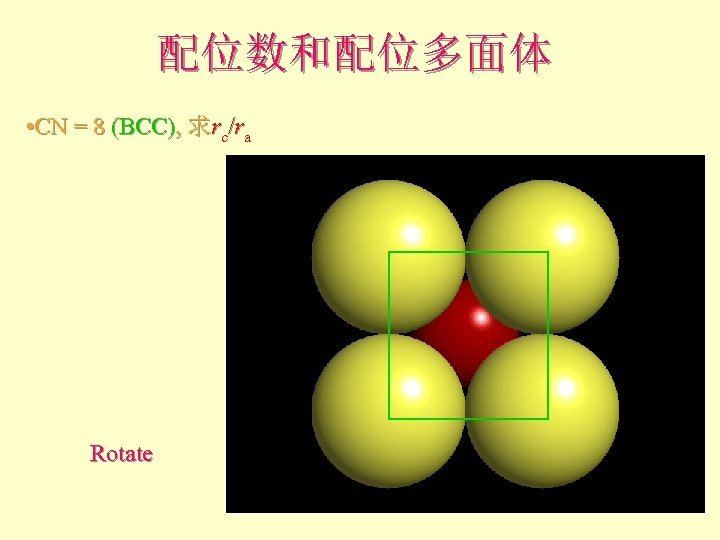
配位数和配位多面体 • CN = 8 (BCC), 求rc/ra Rotate
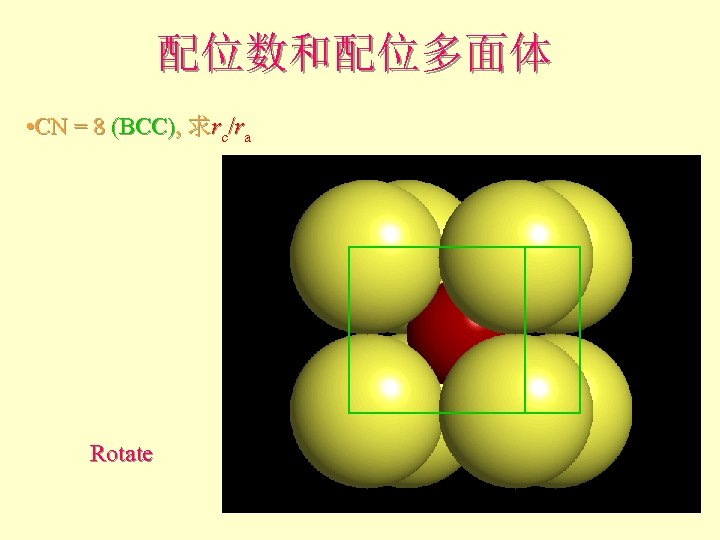
配位数和配位多面体 • CN = 8 (BCC), 求rc/ra Rotate
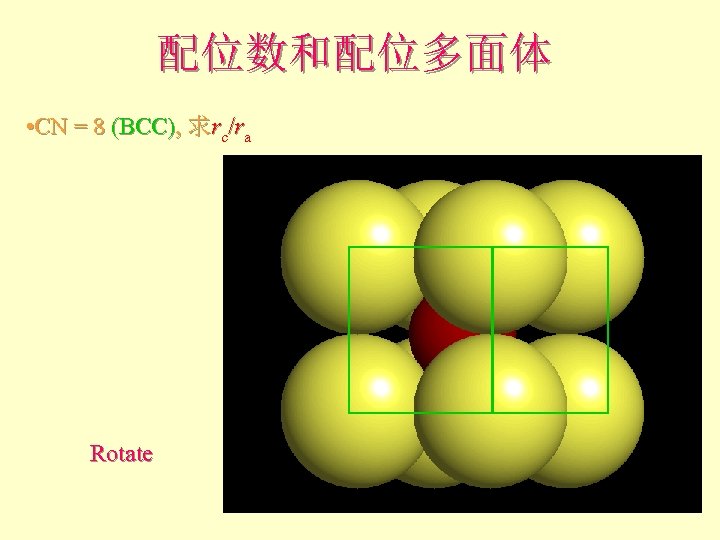
配位数和配位多面体 • CN = 8 (BCC), 求rc/ra Rotate
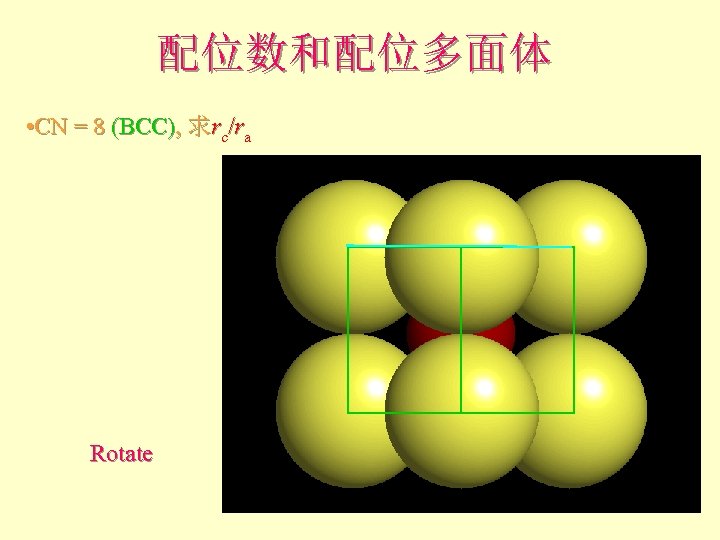
配位数和配位多面体 • CN = 8 (BCC), 求rc/ra Rotate
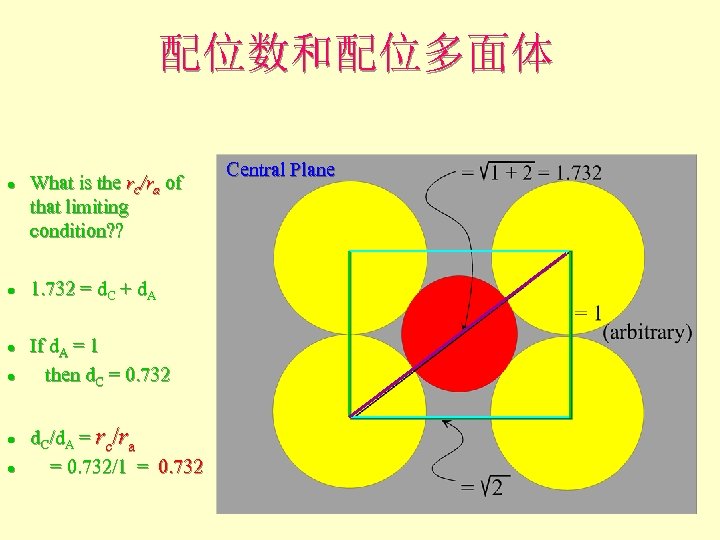
配位数和配位多面体 l l l What is the rc/ra of that limiting condition? ? 1. 732 = d. C + d. A If d. A = 1 then d. C = 0. 732 d. C/d. A = rc/ra = 0. 732/1 = 0. 732 Central Plane
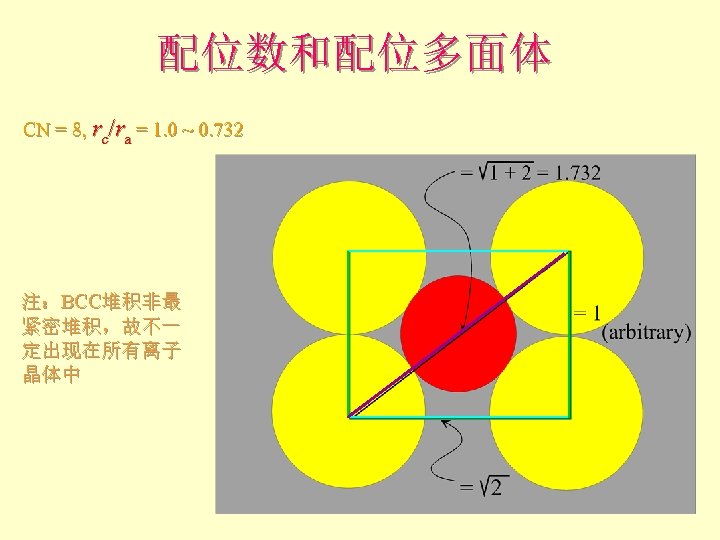
配位数和配位多面体 CN = 8, rc/ra = 1. 0 ~ 0. 732 注:BCC堆积非最 紧密堆积,故不一 定出现在所有离子 晶体中

配位数和配位多面体 l 当rc/ra 小于0. 732,阳离子配位数要降低为 6 What is the rc/ra of l that limiting condition? ? l l l 1. 414 = d. C + d. A If d. A = 1 then d. C = 0. 414 d. C/d. A = rc/ra = 0. 414/1 = 0. 414

配位数和配位多面体 l l 当rc/ra 小于0. 414,阳离子配位数要降低为 4 What is the rc/ra of the limiting condition? ? l 中心到角顶的距离 = 0. 6124 l rc = 0. 612 - 0. 5 = 0. 1124 l l rc / ra = 0. 1124/0. 5 = 0. 225

配位数和配位多面体 l 当rc/ra 小于0. 225,阳离子配位数要降低为 3 l What is the rc/ra of the limiting condition? ? l cos 60 = 0. 5/y y = 0. 577 l rc = 0. 577 - 0. 5 = 0. 077 l rc/ra = 0. 077/0. 5 = 0. 155
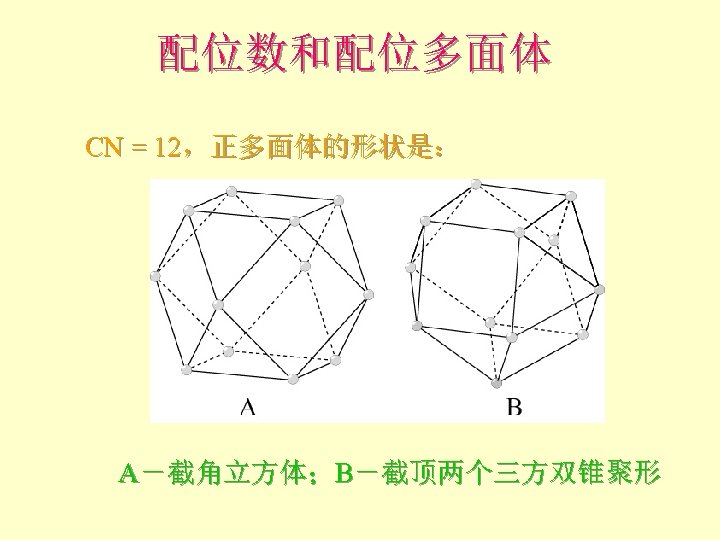
配位数和配位多面体 CN = 12,正多面体的形状是: A-截角立方体;B-截顶两个三方双锥聚形

化学键 l 键 bond 原子(离子、分子)之间的维系力,称为键 F 维系力是化学结合力,则为化学键 F 典型的化学键 F s s 离子键 共价键 金属键 分子键
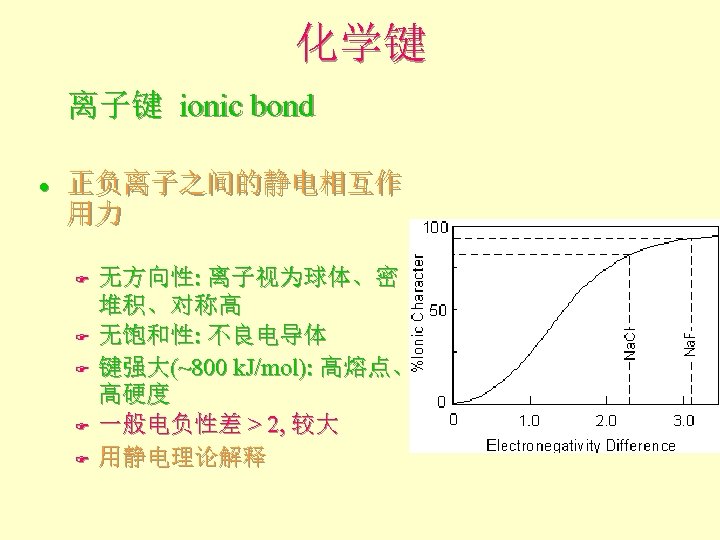
化学键 离子键 ionic bond l 正负离子之间的静电相互作 用力 F F F 无方向性: 离子视为球体、密 堆积、对称高 无饱和性: 不良电导体 键强大(~800 k. J/mol): 高熔点、 高硬度 一般电负性差 > 2, 较大 用静电理论解释
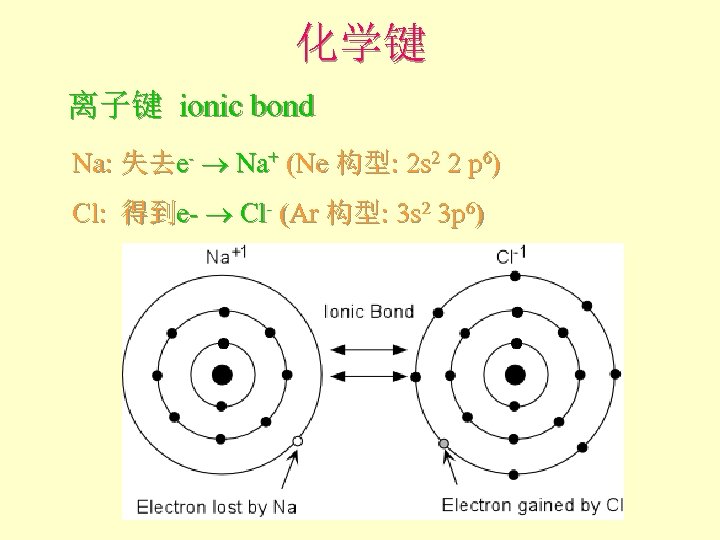
化学键 离子键 ionic bond Na: 失去e- Na+ (Ne 构型: 2 s 2 2 p 6) Cl: 得到e- Cl- (Ar 构型: 3 s 2 3 p 6)

化学键 共价键 covalent bond l 以共用电子对的方式所成的化学键 F F F 具有方向性、饱和性: 低配位数、非密堆积、低密度 无电子和离子: 不导电 键强较大(~400 k. J/mol): 高熔点、高硬度 具有单键、双键、叁键等 一般电负性差小 用量子力学理论、键价理论或分子轨道理论

化学键 共价键 covalent bond F 键能:气态原子A、B生成气态分子AB所释放的能量 A + B AB F F 单位:k. J/mol (+值为释放的能量) 典型的共价键及其键能、键长 共价键 H-H O=O Cl-Cl C-C C=C 键能 432 400 240 345. 6 602 835 键长 0. 74 1. 21 1. 99 1. 53 1. 34 1. 20
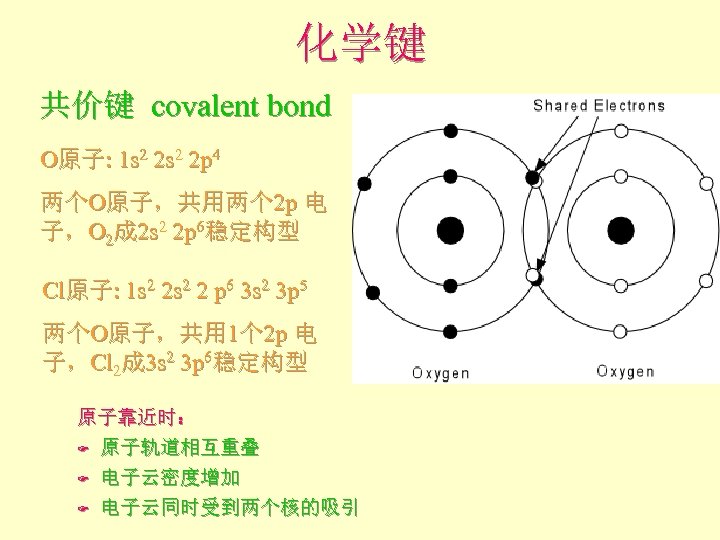
化学键 共价键 covalent bond O原子: 1 s 2 2 p 4 两个O原子,共用两个 2 p 电 子,O 2成 2 s 2 2 p 6稳定构型 Cl原子: 1 s 2 2 p 6 3 s 2 3 p 5 两个O原子,共用 1个 2 p 电 子,Cl 2成 3 s 2 3 p 6稳定构型 原子靠近时: F 原子轨道相互重叠 F 电子云密度增加 F 电子云同时受到两个核的吸引
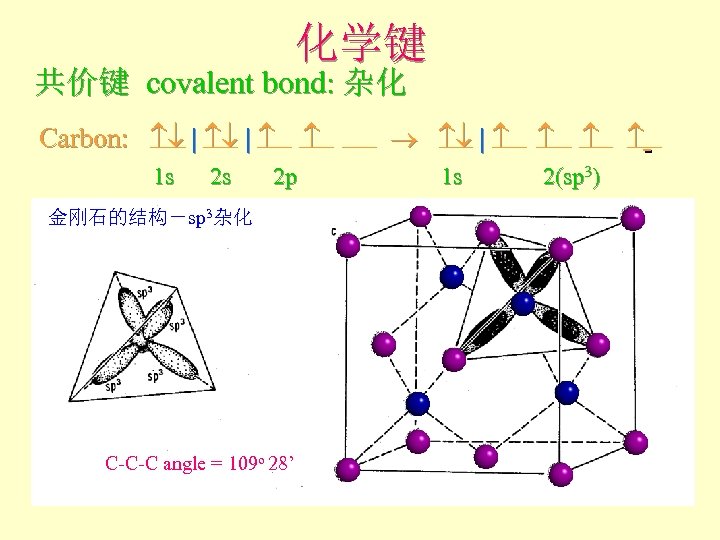
化学键 共价键 covalent bond: 杂化 Carbon: | | 1 s 2 s 2 p 金刚石的结构-sp 3杂化 C-C-C angle = 109 o 28’ 1 s 2(sp 3)

化学键 共价键 covalent bond: 杂化 Carbon: | | 1 s 2 s 2 p 1 s 2(sp 3) • 2 s轨道上1个e-被激发至 2 p轨道: 体系能量增加 4. 16 e. V • 2 p轨道每增加 1个C-C键:能量降低4. 29 e. V
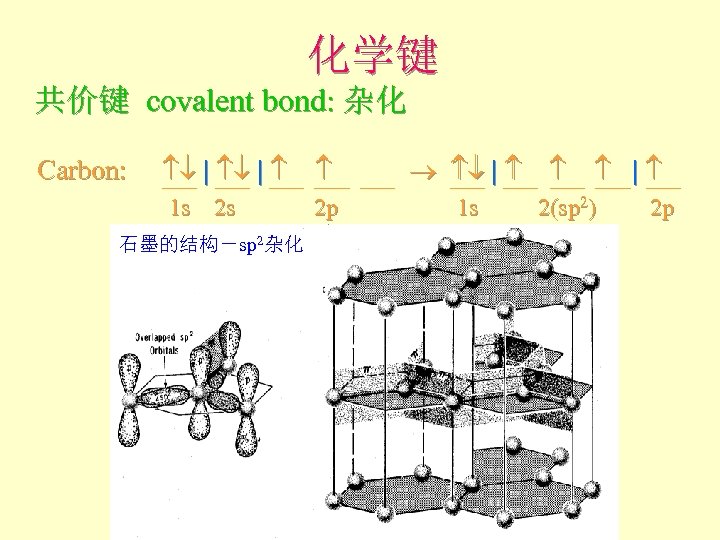
化学键 共价键 covalent bond: 杂化 Carbon: | | 1 s 2 s 2 p 石墨的结构-sp 2杂化 1 s 2(sp 2) 2 p
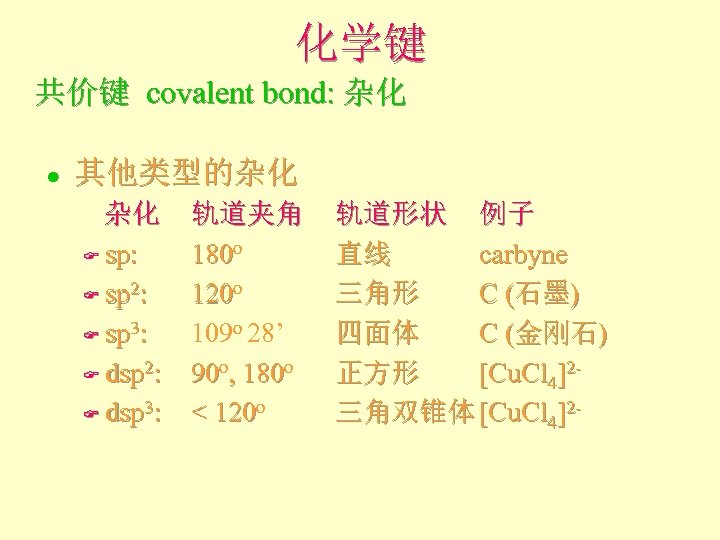
化学键 共价键 covalent bond: 杂化 l 其他类型的杂化 杂化 F sp: F sp 2: F sp 3: F dsp 2: F dsp 3: 轨道夹角 180 o 120 o 109 o 28’ 90 o, 180 o < 120 o 轨道形状 例子 直线 carbyne 三角形 C (石墨) 四面体 C (金刚石) 正方形 [Cu. Cl 4]2三角双锥体 [Cu. Cl 4]2 -
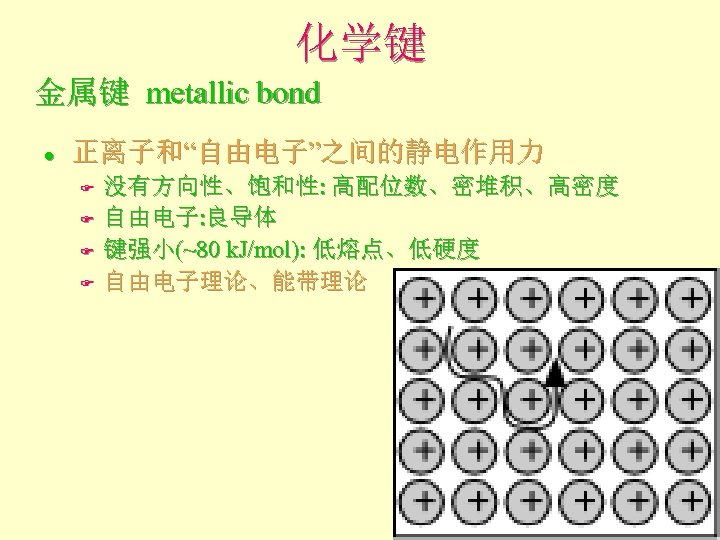
化学键 金属键 metallic bond l 正离子和“自由电子”之间的静电作用力 F F 没有方向性、饱和性: 高配位数、密堆积、高密度 自由电子: 良导体 键强小(~80 k. J/mol): 低熔点、低硬度 自由电子理论、能带理论
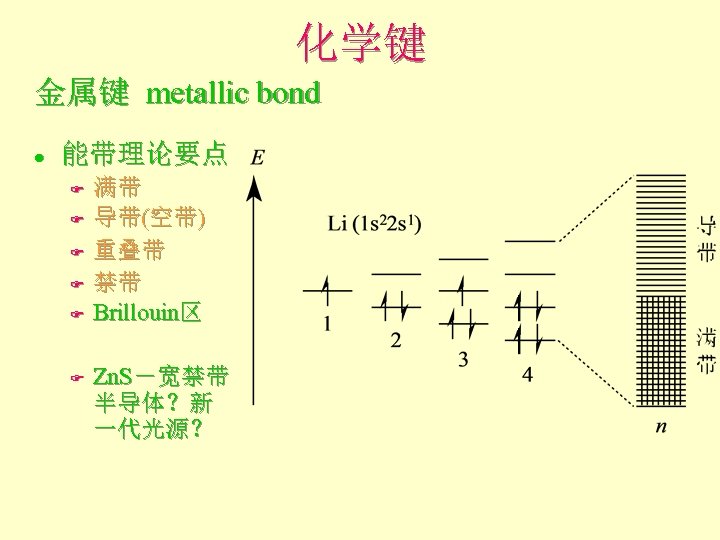
化学键 金属键 metallic bond l 能带理论要点 F F F 满带 导带(空带) 重叠带 禁带 Brillouin区 Zn. S-宽禁带 半导体?新 一代光源?
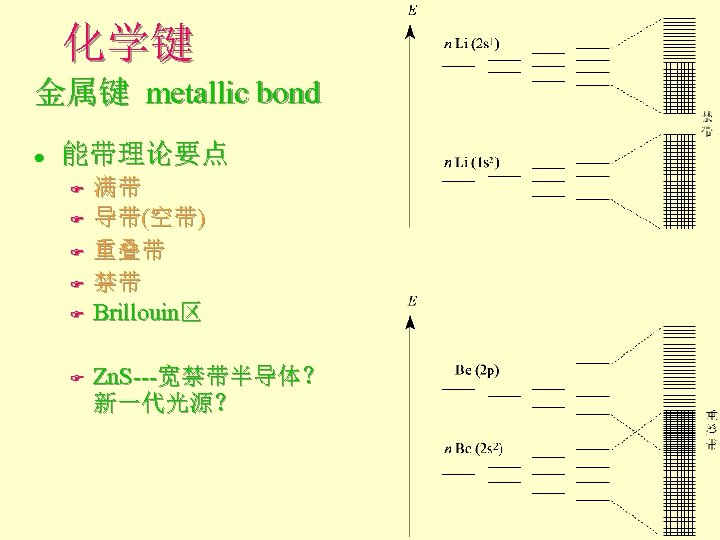
化学键 金属键 metallic bond l 能带理论要点 F F F 满带 导带(空带) 重叠带 禁带 Brillouin区 Zn. S---宽禁带半导体? 新一代光源?
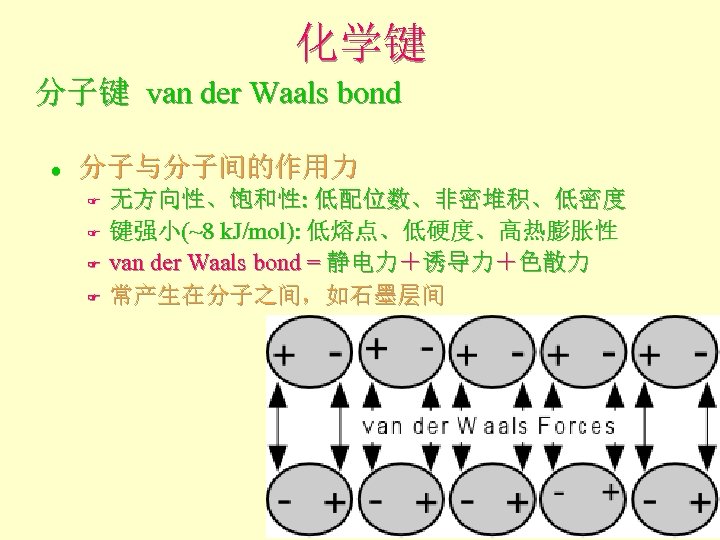
化学键 分子键 van der Waals bond l 分子与分子间的作用力 F F 无方向性、饱和性: 低配位数、非密堆积、低密度 键强小(~8 k. J/mol): 低熔点、低硬度、高热膨胀性 van der Waals bond = 静电力+诱导力+色散力 常产生在分子之间,如石墨层间
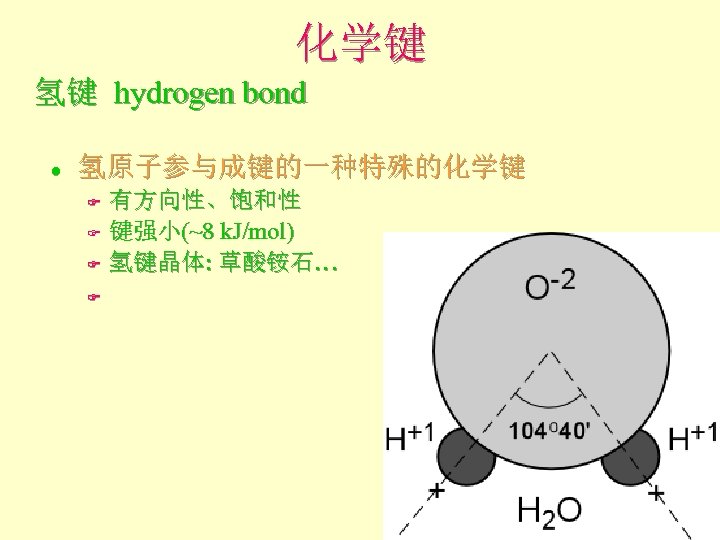
化学键 氢键 hydrogen bond l 氢原子参与成键的一种特殊的化学键 F F 有方向性、饱和性 键强小(~8 k. J/mol) 氢键晶体: 草酸铵石…
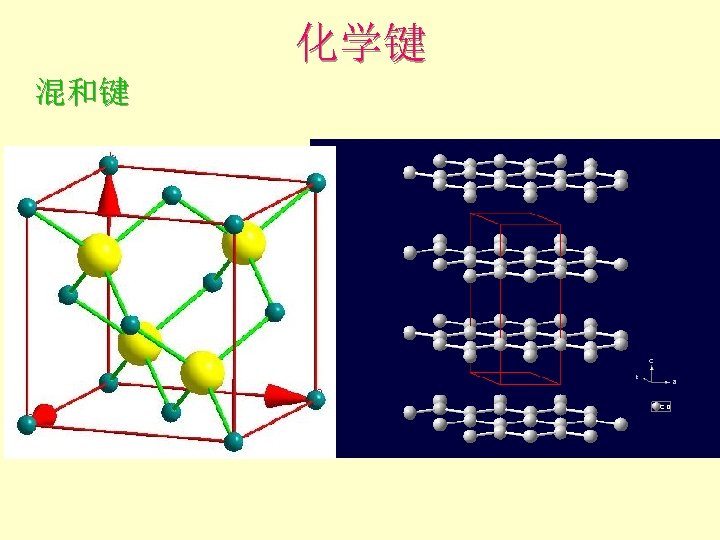
化学键 混和键

离子晶体 Ionic Crystals F F 近似地认为: s 阴离子做密堆积 s 阳离子充填空隙 i 具有不同类型的空隙 i 阳离子占据某一类空隙 i 保持电中性 离子晶体的晶格能U A+(气) + B-(气) AB(晶体) + U F 离子半径及其与CN以及配位多面体的关系

离子晶体 Goldschmidt定律 晶体结构决定于结构基元的相对数量、相对大小和极化性能 l 半径比(r. C/r. A) 离子极化程度 CN 结构 大 弱 8 Cs. Cl Ca. F 2 6 Na. Cl Ti. O 2 小 强 4 Zn. Cl Si. O 2

离子晶体 Pauling规则 1 st Rule l The cation-anion distance = radii Can use RC/RA to determine the coordination number of the cation 半径规则:围绕阳离子形成一个阴离子配位多面体, 阴阳离子间距取决于它们的半径和,配位数取决于其 半径比。

离子晶体 Pauling规则 2 nd Rule 概念:静电键强度(the strength of an electrostatic bond) = valence / CN Cl 如Na. Cl中Na+和Cl-为VI配位, 故Na+的静电键强度 = + 1/6 Cl+的静电键强度 = - 1/6 Cl Cl Cl Na

离子晶体 Pauling规则 • 2 nd Rule: the electrostatic valence principle An ionic structure will be stable to the extent that the sum of the strengths of the electrostatic bonds that reach an ion equal the charge on that ion. l 电价规则:稳定离子结构的离子电价等于 与其相邻异号离子的各静电键强度的总和
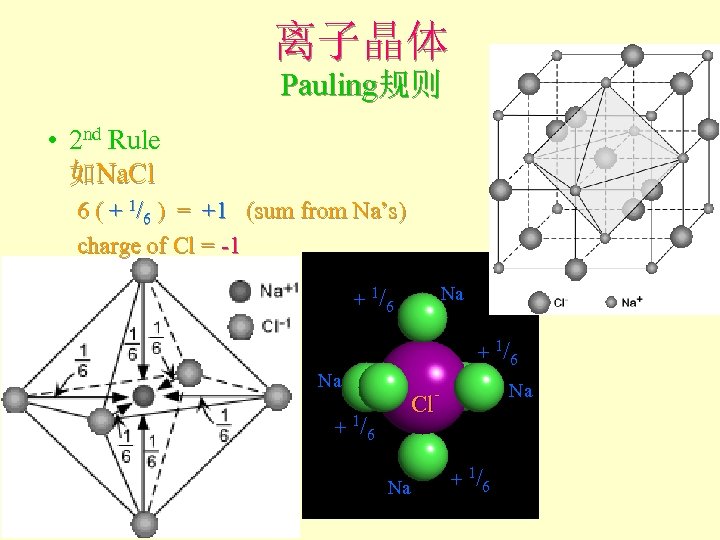
离子晶体 Pauling规则 • 2 nd Rule 如Na. Cl 6 ( + 1/6 ) = +1 (sum from Na’s) charge of Cl = -1 Na + 1/6 Na - Cl. Na + 1/6
![离子晶体 Pauling规则 • 2 nd Rule 如 [CO 3]-2 • C+4的CN = 3,静电键强=4/3 • 离子晶体 Pauling规则 • 2 nd Rule 如 [CO 3]-2 • C+4的CN = 3,静电键强=4/3 •](https://present5.com/presentation/dc5154523c2907b01895280bc11eac71/image-94.jpg)
离子晶体 Pauling规则 • 2 nd Rule 如 [CO 3]-2 • C+4的CN = 3,静电键强=4/3 • 每一个O 2 -贡献 4/3即平衡 • 每一个O 2 -剩下2/3电荷,所 以[CO 3]-2
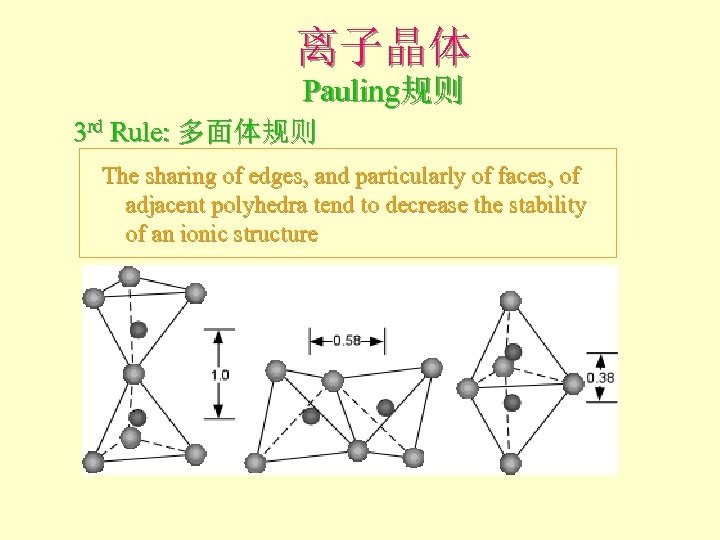
离子晶体 Pauling规则 3 rd Rule: 多面体规则 The sharing of edges, and particularly of faces, of adjacent polyhedra tend to decrease the stability of an ionic structure

离子晶体 Pauling规则 3 rd Rule: 多面体规则 Shared edges, and particularly faces of two anion polyhedra in a crystal structure decreases its stability cc = 1. 0; cc = 0. 72; cc = 0. 58
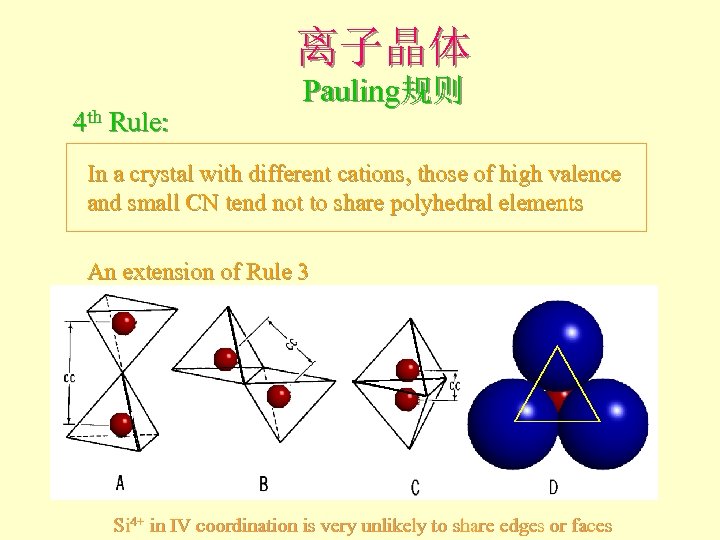
离子晶体 4 th Rule: Pauling规则 In a crystal with different cations, those of high valence and small CN tend not to share polyhedral elements An extension of Rule 3 Si 4+ in IV coordination is very unlikely to share edges or faces

离子晶体 Pauling规则 5 th Rule: 最简规则 The number of different kinds of constituents in a crystal tends to be small. This means that there are only a few different types of cation and anion sites in a crystal. Even though a crystal may have tetrahedral sites, octahedral sites, and cubic sites, most crystals will be limited to this small number of sites, although different elements may occupy similar sites.
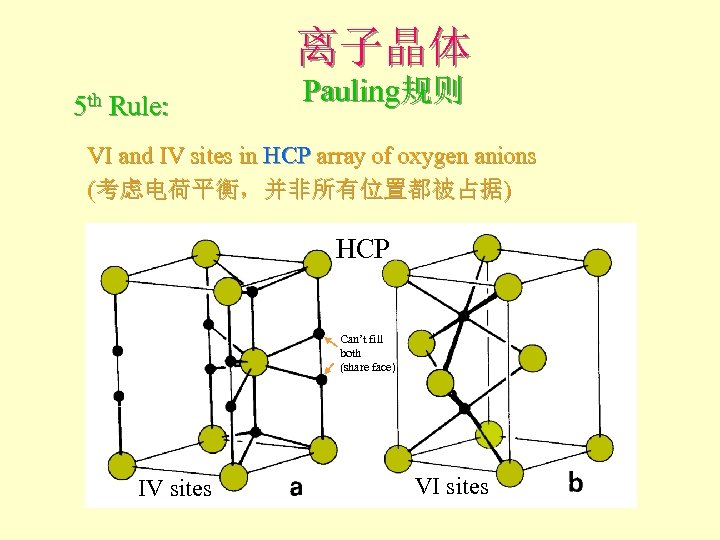
离子晶体 5 th Rule: Pauling规则 VI and IV sites in HCP array of oxygen anions (考虑电荷平衡,并非所有位置都被占据) HCP Can’t fill both (share face) IV sites VI sites
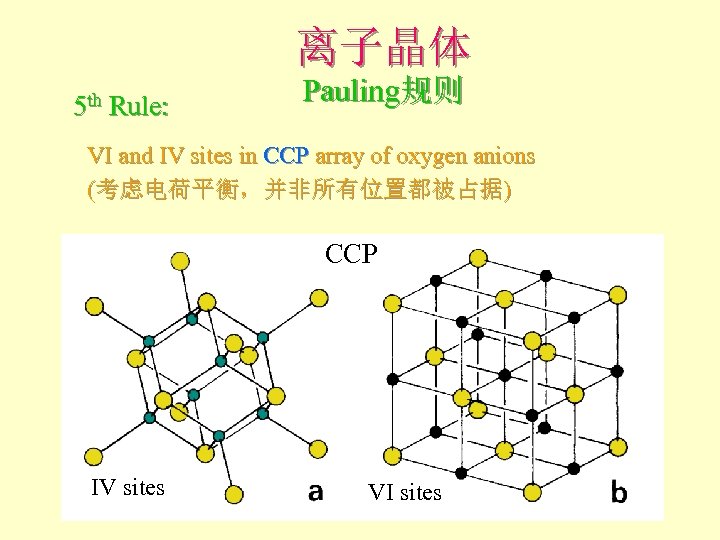
离子晶体 5 th Rule: Pauling规则 VI and IV sites in CCP array of oxygen anions (考虑电荷平衡,并非所有位置都被占据) CCP IV sites VI sites

离子晶体 5 th Rule: Pauling规则 尖晶石结构 (A 2+)IV(B 3+)2 VIO 4 Note CCP O 2 -: ABCABC… 白球:VI sites 蓝球:IV sites
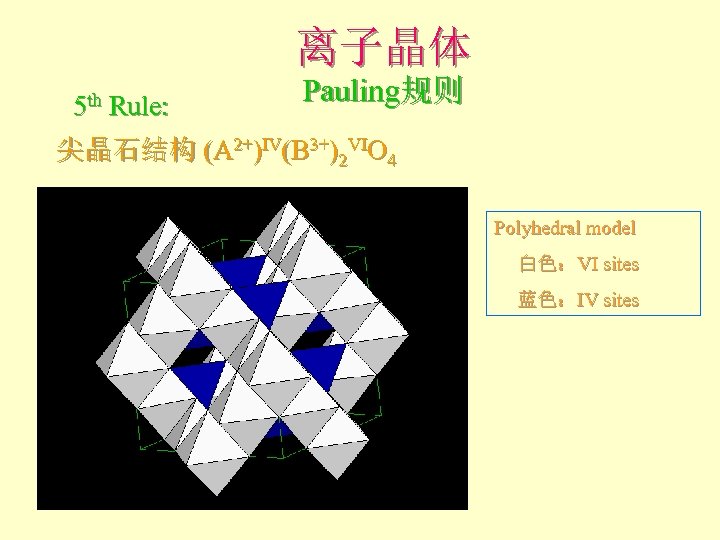
离子晶体 5 th Rule: Pauling规则 尖晶石结构 (A 2+)IV(B 3+)2 VIO 4 Polyhedral model 白色:VI sites 蓝色:IV sites

离子晶体 5 th Rule: Pauling规则 尖晶石结构 (A 2+)IV(B 3+)2 VIO 4 旋转一定角度观察: Not all are occupied: 1/8 of IV sites 1/2 of VI sites
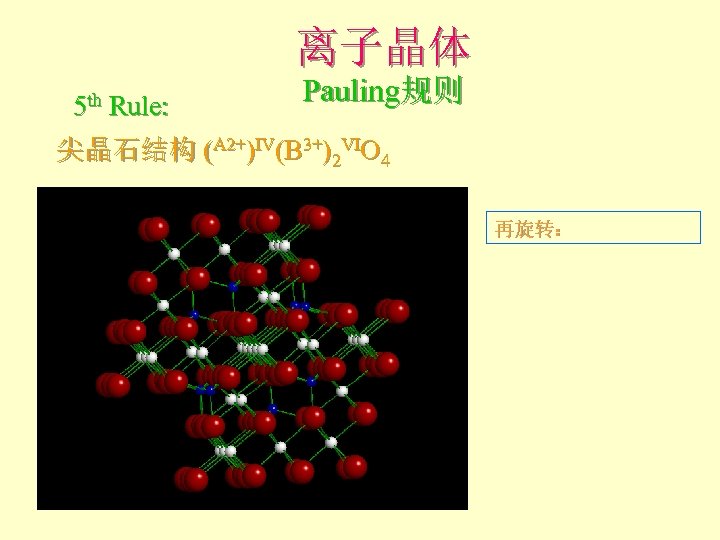
离子晶体 5 th Rule: Pauling规则 尖晶石结构 (A 2+)IV(B 3+)2 VIO 4 再旋转:
![离子晶体 5 th Rule: Pauling规则 尖晶石结构 (A 2+)IV(B 3+)2 VIO 4 旋转至沿[010]观察 The order 离子晶体 5 th Rule: Pauling规则 尖晶石结构 (A 2+)IV(B 3+)2 VIO 4 旋转至沿[010]观察 The order](https://present5.com/presentation/dc5154523c2907b01895280bc11eac71/image-105.jpg)
离子晶体 5 th Rule: Pauling规则 尖晶石结构 (A 2+)IV(B 3+)2 VIO 4 旋转至沿[010]观察 The order becomes apparent
dc5154523c2907b01895280bc11eac71.ppt