第 4章 4 1 概述 4 2 决策树分类方法

第 4章 4. 1 概述>> 4. 2 决策树分类方法>> 4. 3 朴素贝叶斯分类方法>> 4. 4 最近邻KNN分类方法>> 4. 5 集成分类器>> 4. 6 分类方法评价>> 4. 7 综合例子>> 分类

开篇案例（1）一家著名高尔夫俱乐部的经理，被每天需要的雇员数量问题所困扰。因为某些天很多人都来玩高尔夫，以至于所有员都忙得团团转还是应付不过来，而有些天不知道什么原因却一个人也不来，俱乐部因为雇员数量不合适而浪费了不少资金。经理希望通过下周天气预报寻找什么时候人们会打高尔夫，以适时调整雇员数量。因此首先他必须了解人们决定是否打球的原因。在 2周时间内他们记录了每天的天气信息以及顾客是否光顾俱乐部的信息: 天气状况有晴、云和雨；气温用华氏温度表示；相对湿度用百分比；还有有无风。当然还有顾客是否在这些日子光顾俱乐部。最终他得到了14列 5行的数据表格，如表 4 -1。如何通过分析顾客 2周的历史数据，判断在什么情况下会有人来打打高尔夫？这是一个典型的决策树分类问题。使用决策树在该数据集上建立分类预测模型，可以发现如下的分类模式：（1）如果天气是多云，人们总是选择玩高尔夫，而只有少数很着迷的甚至在雨天也会玩；（2）顾客不喜欢湿度高于70%的天气；（3）如果雨天还有风的话，就不会有人打了。最后David（老板）在晴天，潮湿的天气或者刮风的雨天解雇了大部分员，因为这种天气不会有人打高尔夫，而其他的天气会有很多人打高尔夫，因此可以雇用一些临时员来作。这种利用已有观测数据建立决策树，并用决策树来确定新的对象的类别的方法就是分类要研究的问题。

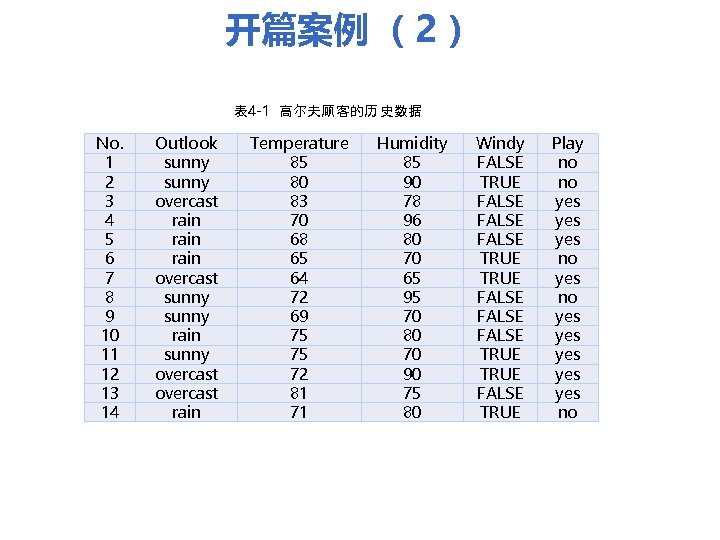
开篇案例（2）表 4 -1 高尔夫顾客的历史数据 No. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Outlook sunny overcast rain overcast sunny rain sunny overcast rain Temperature 85 80 83 70 68 65 64 72 69 75 75 72 81 71 Humidity 85 90 78 96 80 70 65 95 70 80 70 90 75 80 Windy FALSE TRUE FALSE FALSE TRUE FALSE TRUE Play no no yes yes yes no

4. 1 概述（1） 4. 1. 1 基于决策树的分类方法 4. 1. 2 贝叶斯分类方法 4. 1. 3 k-最近邻分类方法 4. 1. 4 神经网络方法

4. 1 概述（2） l l l 分类是对数据集进行学习并构造一个拥有预测功能的分类模型，用于预测未知样本的类标号，把类标号未知的样本映射到某个预先给定的类标号中。或者说，分类就是利用训练数据中学习到的规律来确定未知样本的类别。例如，根据银行客户信用贷款的历史数据，使用分类可以构造‘拖欠贷款’和‘非拖欠贷款’两类客户的模型，对于将要申请信用贷款的客户，可以根据分类模型和该客户的特征来预测该客户是否会拖欠贷款，从而决定是否同意给该客户贷款。分类方法已被广泛应用于各行各业，如在金融市场预测、信用评估、医疗诊断、市场营销等诸多实际应用领域。在证券市场中，分类器被用于预测股票未来的走向；在银行、保险等领域中，利用已有数据建立分类模型，评估客户的信用等级；在市场营销中，利用历史的销售数据，预测某些商品是否可以销售、预测广告应该投放到哪个区域、预测某客户是否会成为商场客户从而实施定点传单投放等。

4. 1 概述（3）分类过程一般包括三个环节：（1）将数据集划分为训练集和测试集两部分；（2）通过分析训练集的特点来构建分类模型；（3）对测试集用建立的分类模型进行分类，评估分类准确度，通常使用分类准确度高的分类模型对类标号未知的样本数据进行分类。 l l l 为建立模型而被分析的数据集称为训练数据集，其中单个元组称为训练样本。每个训练样本包括多个属性，其中有一个属性决定该元组属于一个预定义的类，该属性称为类标号属性（class label attribute）或目标属性，其他属性称为预测属性。分类的目的就是对训练样本进行分析，根据其预测属性特征，得出一个精确的分类模型，据此对目标属性未知的元组进行类归属判断。分类方法有很多，本章主要介绍决策树分类方法，贝叶斯分类方法，最近邻分类方法和集成分类方法。

4. 2 决策树分类方法 4. 2. 1 决策树的基础概念 4. 2. 2 决策树的构建 4. 2. 3 Hunt算法 4. 2. 4 C 4. 5分类算法 4. 2. 5 CART算法 4. 2. 6 C 4. 5与CART算法的区别 4. 2. 7 决策树分类算法的优点

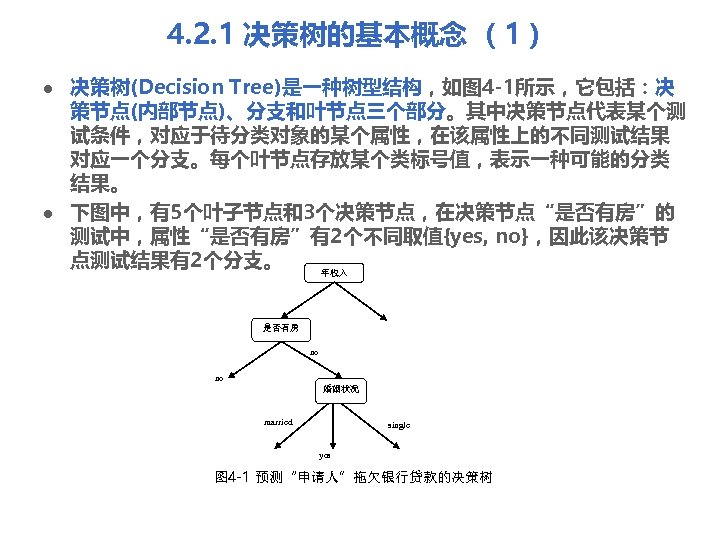
4. 2. 1 决策树的基本概念（1） l l 决策树(Decision Tree)是一种树型结构，如图 4 -1所示，它包括：决策节点(内部节点)、分支和叶节点三个部分。其中决策节点代表某个测试条件，对应于待分类对象的某个属性，在该属性上的不同测试结果对应一个分支。每个叶节点存放某个类标号值，表示一种可能的分类结果。下图中，有5个叶子节点和3个决策节点，在决策节点“是否有房”的测试中，属性“是否有房”有2个不同取值{yes, no}，因此该决策节点测试结果有2个分支。年收入是否有房 no no 婚姻状况 married single yes 图 4 -1 预测“申请人”拖欠银行贷款的决策树

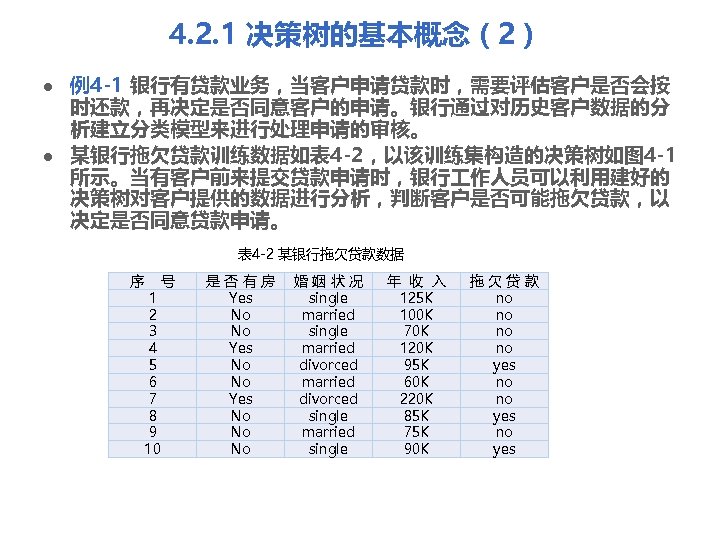
4. 2. 1 决策树的基本概念（2） l l 例4 -1 银行有贷款业务，当客户申请贷款时，需要评估客户是否会按时还款，再决定是否同意客户的申请。银行通过对历史客户数据的分析建立分类模型来进行处理申请的审核。某银行拖欠贷款训练数据如表 4 -2，以该训练集构造的决策树如图 4 -1 所示。当有客户前来提交贷款申请时，银行作人员可以利用建好的决策树对客户提供的数据进行分析，判断客户是否可能拖欠贷款，以决定是否同意贷款申请。表 4 -2 某银行拖欠贷款数据序 1 2 3 4 5 6 7 8 9 10 号是否有房 Yes No No No 婚姻状况 single married divorced single married single 年收入 125 K 100 K 70 K 120 K 95 K 60 K 220 K 85 K 75 K 90 K 拖欠贷款 no no yes

4. 2. 2 决策树的构建 (1) 在构建决策树过程中关键要解决 2个问题：（1）如何选择合适的属性作为决策树的节点去划分训练样本；（2）在什么时候（情况）停止划分，从而得到大小合适的决策树。 l （1）决策树的属性选择 l 属性选择是决策树算法中重要的步骤，每次选择最有利于分类的属性或最重要的属性，或分类能力最强的属性。通常需要最大限度地增加样本集纯度，而且不要产生样本数量太少的分支。如果数据均匀地分布于各个类中，则数据的不纯度就大，反之，数据的不纯度就小。根据某个属性的不同值划分数据时，会导致数据不纯度的减少。 l 常见的属性选择标准包括熵（entropy）、信息增益（information gain）、信息增益率（information ga in ratio）和Gini系数。 l 在决策树算中，C 4. 5使用信息增益率作为决策树构建时属性的选择标准，CART使用Gini系数作为决策树构建时属性的选择标准。

4. 2. 2 决策树的构建 (2) （a）信息熵 l熵（entropy, 也称信息熵）是数据集中的不确定性、突发性或随机性程度的度量。假定S为训练集，S的目标属性C具有m个可能的类标号值， C={C 1, C 2, …, Cm}，Ci在所有样本中出现的频率为 (i=1, 2, 3, …, m)，则该训练集S所包含的信息熵定义为： l熵越小表示样本对目标属性的分布越纯，特别地熵为 0则意味着所有样本的目标属性取值相同。反之，熵越大表示样本对目标属性分布越混乱。

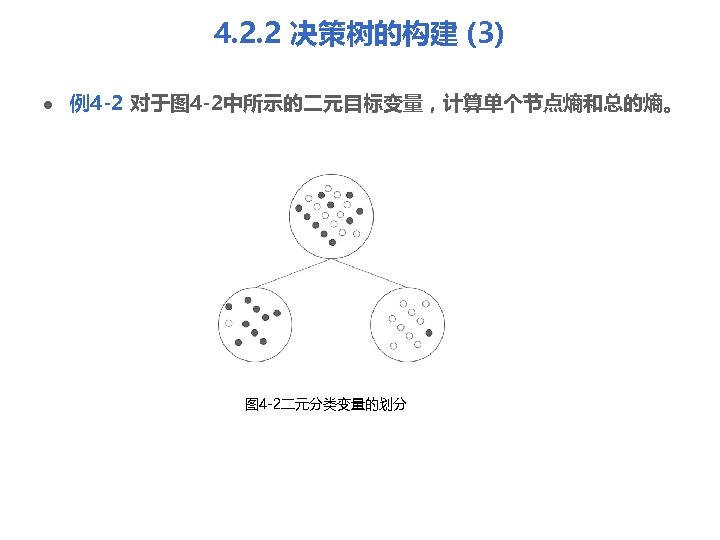
4. 2. 2 决策树的构建 (3) l 例4 -2 对于图 4 -2中所示的二元目标变量，计算单个节点熵和总的熵。图 4 -2二元分类变量的划分

4. 2. 2 决策树的构建 (4) l l 解：划分前：对于划分前单个节点的熵，计算如下：在这个例子中，暗点(dark)和亮点(light)都是 10个，各占一半，即 p(dark)=p(light)=0. 5，将其代入上述公式中得：划分后：划分成两个节点，其中一个节点有1个暗点和9个亮点，而另一个节点有 9个暗点和1个亮点。显然，它们具有相同的熵为：为计算划分后的熵的总和，用每个节点的熵乘以到达该节点的记录的比例，并把它们求和得到平均值。在本例中，每个新节点接收了一半记录，因此划分后总熵为： 0. 5× 0. 47+0. 5× 0. 47=0. 47。

4. 2. 2 决策树的构建 (5) l l （b）信息增益是划分前样本数据集的不纯程度（熵）和划分后样本数据集的不纯程度（熵）的差值。假设划分前样本数据集为S，并用属性A来划分样本集S，则按属性A划分S的信息增益Gain(S, A)为样本集S的熵减去按属性A划分S后的样本子集的熵：按属性A划分S后的样本子集的熵定义如下：假定属性A有k个不同的取值，从而将S划分为k个样本子集{S 1, S 2, …, Sk}，则按属性A划分S后的样本子集的信息熵为: 信息增益越大或划分后的信息熵越小，说明使用属性A划分后的样本子集越纯，越有利于分类。信息增益是决策树常用的划分属性选择准则，在树的每个结点上选择具有最高信息增益的属性作为当前结点的划分属性。

4. 2. 2 决策树的构建 (6) （c）信息增益率 l使用信息熵或信息增益来选择分裂属性时，它容易倾向于选择具有大量不同取值的属性，从而产生许多小而纯的子集，那么产生的决策树具有非常多的分支，且每个分支产生的子集的熵均接近于0。显然，这样的决策树是没有实际意义的。因此，Quinlan提出使用信息增益率来选择划分属性。 l假设划分前样本数据集为S，并用属性A来划分样本集S，则按属性A划分S的信息增益率定义为： l按属性A划分S后的样本子集的定义如下：假定属性A有k个不同的取值，从而将S划分为k个样本子集{S 1, S 2, …, Sk}，则定义为:

4. 2. 2 决策树的构建 (7) l l 例4 -3 对于表 4 -2所示的数据集S，计算按照婚姻状况属性进行分裂的信息增益率。解： “婚姻状况”属性将数据集S划分为三个子集，与 single, married, divorced对应的三个子集的目标属性（yes/no）分布为： 2/2，0/4，1/1。于是：那么，

4. 2. 2 决策树的构建 (8) （4）Gini系数 l. Gini系数是另一种度量数据不纯度的函数，如果数据均匀地分布于各个类中，则数据的不纯度就大，反之，数据的不纯度就小。根据某个属性的不同值划分数据时，会导致数据不纯度的减少。设t为决策树中的某个节点，Gini系数的计算公式如下： l其中，m为当前属性下测试输出的类别数，为节点t中样本测试输出取类别j的概率。对节点t而言，G(t)越小，意味着该节点中所包含的样本越集中在某一类上，即该节点越纯。当节点样本的测试输出均取同一类别值时，输出变量取值的差异性最小，Gini系数为 0，而当各类别取概率值相等，测试输出取值的差异性最大，Gini系数为

4. 2. 2 决策树的构建 (9) （e）连续属性的信息熵和Gini系数计算 l在以上关于信息熵、信息增益和Gini系数的计算中，都是使用分类属性作为划分进行说明。对于连续属性，信息熵和Gini系数的计算方法与分类属性具有很大的不同。 u首先对连续属性值进行递增排序，将每对相邻值的中点看作可能的分裂点，而将数据集分为两组； u对于每个可能的分裂点，计算信息熵和Gini系数； u最后选取信息熵或Gini系数最小的分裂点为最佳分裂点。

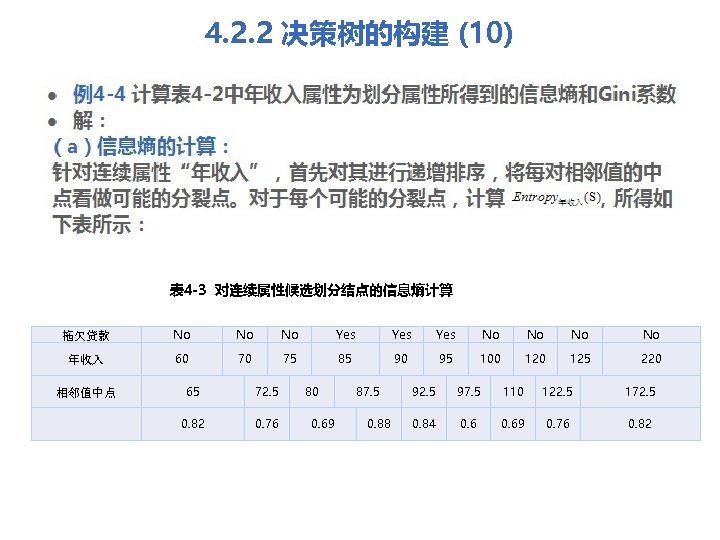
4. 2. 2 决策树的构建 (10) 例4 -4 计算表 4 -2中年收入属性为划分属性所得到的信息熵和Gini系数 l 解：（a）信息熵的计算：针对连续属性“年收入”，首先对其进行递增排序，将每对相邻值的中点看做可能的分裂点。对于每个可能的分裂点，计算，所得如下表所示： l 表 4 -3 对连续属性候选划分结点的信息熵计算拖欠贷款 No No No Yes Yes No No 年收入 60 70 75 85 90 95 100 125 220 相邻值中点 65 72. 5 0. 82 0. 76 80 0. 69 87. 5 0. 88 92. 5 97. 5 110 122. 5 172. 5 0. 84 0. 69 0. 76 0. 82

4. 2. 2 决策树的构建 (11) 以中点 87. 5为例，计算。年收入小于87. 5的记录中，yes对应 1条，no对应 3条；年收入大于87. 5的记录中，yes对应 2条，no对应 4 条。选择值最小的分裂点即 97. 5作为年收入属性的最佳分裂点。划分前所有数据的信息熵为，信息增益值为：此为可能分裂点的最大信息增益。

4. 2. 2 决策树的构建 (12) （b）Gini系数的计算 l 对于连续属性Gini系数的计算，同样对数据按升序排序，将每对相邻值的中间值作为可能的分裂点，取差异性损失值最大的分裂点分隔属性。 l下面仅介绍以 92. 5作为分裂点时属性年收入划分节点分组的差异性损失计算，其它分裂点的分组划分计算留给读者自己完成。当前表示年收入小于92. 5的样本，表示年收入大于等于92. 5的样本。划分前所有数据的 Gini系数为： l划分后差异性损失为：表 4 -4 对年收入属性候选划分结点的Gini系数计算拖欠贷款年收入相邻值中点差异性损失 No 60 65 0. 02 No 70 72. 5 0. 045 No 75 80 0. 077 Yes 85 Yes No No No 90 95 100 125 87. 5 92. 5 97. 5 110 122. 5 0. 003 0. 02 0. 12 0. 077 0. 045 No 220 172. 5 0. 02

4. 2. 2 决策树的构建 (13) （2）获得大小合适的树 l决策树学习的目的是希望生成能够揭示数据集结构并且预测能力强的一棵树，在树完全生长的时候有可能预测能力反而降低，为此通常需要获得大小合适的树。 l一般来说有两种获取方法: u 一种为定义树的停止生长条件, 常见条件包括最小划分实例数、划分阈值和最大树深度等。 u 另一种方法是对完全生长决策树进行剪枝，方法是对决策树的子树进行评估，若去掉该子树后整个决策树表现更好，则该子树将被剪枝。

4. 2. 2 决策树的构建 (14) l 决策树剪枝(pruning)的原则是去除对未知样本预测准确度低的子树，建立复杂度较低且容易理解的树。通常有预剪枝(prepruning)和后剪枝(postpruning)两种基本方法来简化决策树。预剪枝的目标是控制决策树充分生长，通过事先指定一些控制参数来完成：（1）决策树最大深度：如果决策树的层数已经达到指定深度，则不再进行划分。 (2)树中父节点和子节点所包含的最少样本量或比例：如果节点所包(2)含的样本量已低于最少样本量或比例，则不再划分；如果划分后生成的某个子节点所包含的样本量低于最小样本量或比例，则不再进行划分。 (3)树节点中测试输出结果的最小差异减少量：如果划分后所产生的测试输出结果(如信息熵、Gini系数等度量)差异性变化量小于指定的阈值，则不再进行划分。 l

4. 2. 2 决策树的构建 (15) l l 后剪枝首先生成一棵完全生长的树，然后根据一定的规则，剪去决策树中不具有代表性的叶节点或子树，以创建一个更稳定的模型。剪枝方法是对决策树的子树进行评估，若去掉该子树后整个决策树表现更好(误分类率或模型复杂性降低)，则该子树将被剪枝。基本过程：从树的叶节点开始，检查每个非叶节点，如果以某叶节点或其子节点中使用频率最高的子节点替换该非叶节点后，将使得整个决策树的误分类率降低，则做相应剪枝。图 4 -3在复杂树的内部，有更简单、稳定的树

4. 2. 3 Hunt算法 l l Hunt算法是许多经典决策树算法如ID 3、C 4. 5的基础. Hunt算法对决策树的建立过程描述如下，假定Dt是与结点t相关联的训练记录集，C={C 1, C 2, …, Cm}是类标号，Hunt算法的递归定义如下： (1)如果Dt中所有记录都属于同一个类Ci(1≤i≤m), 那么t是叶结点，用类标号Ci进行标记。 (2)如果Dt包含属于多个类的记录, 则选择一个属性测试条件，将记录划分为更小的子集。对于测试条件的每个输出，创建一个子女节点，并根据测试结果将Dt中的记录分布到子女节点中，然后对每个子女节点递归调用该算法。

4. 2. 4 C 4. 5分类算法（1） l C 4. 5是Quinlan 1993年在ID 3算法的基础上提出的改进算法。（1）分裂属性选择 l C 4. 5以信息增益率作为属性选择标准，通过属性的分裂信息调节信息增益，不仅考虑信息增益的大小程度，还考虑为获得信息增益所付出的“代价”。这样如果某个属性有较多的分类取值，则它的信息熵会偏大，但信息增益率由于考虑了分裂信息而降低，进而消除了属性取值数目所带来的影响。

4. 2. 4 C 4. 5分类算法（2）对缺失数据的处理 l. C 4. 5算法采用概率的方法，为缺失值的每个可能值赋予一个概率，而不是将最常见的值替代该缺失值。改进对信息增益、分裂信息的计算方法，使得算法能够继续依据信息增益率来选择决策树中非叶节点的划分属性。 l方法基本描述如下：假定S为训练集，属性A在样本集中存在部分缺失值，属性A的信息增益计算方法改为 l在属性A的分裂信息的定义中，将属性A未知的样本子集作为额外的子集 Sunkown，即将缺失值看成一个类别，分裂信息按照公式进行计算。

4. 2. 4 C 4. 5分类算法（3） (3) C 4. 5算法描述 l. C 4. 5决策树的建立过程可以分为两个过程，首先使用训练集数据依据 C 4. 5树生长算法构建一棵完全生长的决策树，然后对树进行剪枝，最后得到一棵最优决策树。C 4. 5决策树的算法步骤： a)如果训练集全部属于同一个类别，那么创建一个叶结点； b)否则计算训练集中每个属性的信息增益率，选择增益率最大的属性为决策属性，并以该决策属性创建结点； c)对第二步中决策属性结点的每个取值都添加一个分支； d)对于每个分支的训练集，转第一步。

4. 2. 4 C 4. 5分类算法（4） C 4. 5决策树的剪枝处理算法描述如下： a)计算待剪子树中叶结点的加权估计误差； b)如果待剪子树是一个叶子结点，则结束； c)否则，计算其子树误差和所有的分支误差； d)如果叶结点误差小于子树误差和最大的分支误差，则剪枝，设置待剪子树的根节点为叶结点； e)如果最大的分支误差小于叶结点误差和子树误差，则剪枝，以误差最大的分支体会待剪子树； f)否则，不剪枝。

4. 2. 4 C 4. 5分类算法（5） l l l C 4. 5只适合于能够驻留于内存的数据集，当训练集大得无法在内存容纳时，程序将无法运行。为适应大规模数据集，在C 4. 5后出现有SLIQ和SPRINT算法。 C 4. 5后续发展为商用的C 5. 0，它在C 4. 5的基础上做了一些改进，如使用提升技术，生成一系列决策树然后集体投票决定分类结果；支持新的数据类型，如日期等；规则集没有先后顺序，而是所有匹配规则进行投票，更易解释。 C 4. 5在进行属性选择时，上一层次用过的属性不再考虑，而C 5. 0在进行属性选择时，每次都要考虑所有属性。

4. 2. 4 C 4. 5分类算法（6）例4 -5 根据C 4. 5算法对表 4 -2数据集进行训练，建立一棵C 4. 5决策树。解：(a)首先计算样本集S的信息熵 (b)计算各属性对样本集的信息熵和信息增益。这里仅列举属性 “是否有房”对样本的信息熵，先分别计算该属性“yes”, “no”所包含的信息熵。“是否有房”属性值“yes”对应 3 条记录，其中“是否拖欠贷款”为“yes”的有0条，“no” 的有3条。“是否有房”属性值“no”对应 7条记录，其中“ 是否拖欠贷款”为“yes”的有3条，“no”的有4条。

4. 2. 4 C 4. 5分类算法（7） (c)同样的方法算出 (d)针对数值属性“年收入”。由例4 -2可知，97. 5作为年收入属性的最佳分裂点。

4. 2. 4 C 4. 5分类算法（8） (e)计算各个属性的分裂信息和信息增益率, 对于“是否有房”属性，取值为yes的有3条，取值为no有7条，因此有对于“婚姻状况”属性，取值为Single的有4条，取值为 Married的有4条，取值为Divorced的有2条，因此有：

4. 2. 4 C 4. 5分类算法（9） l l 对于“年收入”属性，分裂点 97. 5将年收入值划分为两个区间，大于97. 5的有4条记录，小于97. 5的有6条记录，因此有：可以看出，“年收入”属性的信息增益率是最大的，所以选择 “年收入”属性作为决策树的根结点，产生 2个分支，对每个分支重复进行上面的运算过程，即可生成整个决策树，结果如图 4 -4所示。

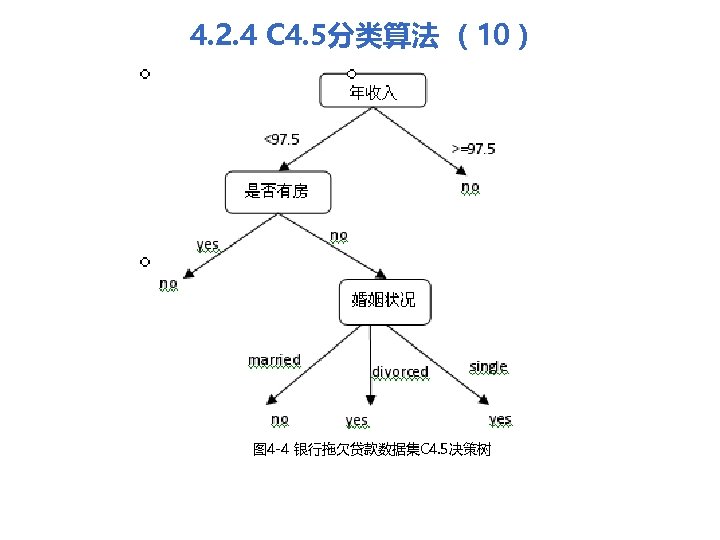
4. 2. 4 C 4. 5分类算法（10）图 4 -4 银行拖欠贷款数据集C 4. 5决策树

4. 2. 5 CART算法（1） l CART决策树采用的是二元递归划分方法，能够处理连续属性和分类属性作为预测变量和输出变量下的分类，当输出变量是分类属性数据时，所建立的为分类树，用于分类的预测。当输出变量为数值型变量时，所建立的决策树称为回归树，用于数值的预测。 (1) CART算法的基本概念 l l 分类回归树的建树过程是对训练集的反复划分的过程，涉及如何从多个属性中选择当前最佳划分属性的问题。在分类回归树的建树过程中，针对每个属性都要进行相应的计算以确定最佳划分属性，另外针对 CART的分类树和回归树，它们的计算方法有所不同，数值型和分类型属性变量的计算法方法也存在差异。设训练样本集S={A 1, A 2, …, Am，Y}，其中A 1到Am称为属性向量，Y 称为类标号向量。当Y是连续型数据时，称为回归树，当Y是离散型数据时，称为分类树。

4. 2. 5 CART算法（2） (a)分类树的属性选择 l对于CART分类树的分裂属性选择，分类型属性和数值型属性处理得方法有所不同。 l对于分类树使用Gini系数来度量对某个属性变量测试输出的两组取值的差异性。由于CART只能建立二叉树，对于取多个值的属性变量，需要将多类别合并成两个类别，形成“超类”，然后计算两“超类”下样本测试输出取值的差异性。 l对于数值型属性，方法是将数据按升序排序，然后从小到大依次以相邻数值的中间值作为分隔，将样本分为两组，并计算所得组中样本测试输出取值的差异性。 l理想的分组是使两组中样本测试输出取值的差异性总和达到最小，即“ 纯度”最大，也就是使两组输出变量取值的差异性下降最快，“纯度”增加最快。

4. 2. 5 CART算法（3） (b)回归树的属性选择 l 回归树确定当前最佳分裂属性的策略与分类树不同在于度量节点测试输出值差异性的指标。由于回归树的测试输出为数值型，以方差作为差异性的指标，其定义为： l l 其中，t为节点，N为节点t所含的样本个数，yi(t)为节点t中测试输出变量值，为节点t中测试输出变量的平均值。于是，差异性损失的度量指标为方差的减少量，其定义为：其中，R(t)为分组前输出变量的方差，、和、分别为分组后右子树的方差和样本量以及左子树的方差和样本量。使达到最大的属性变量为当前最佳划分属性变量。

4. 2. 5 CART算法（4） (2)CART算法的步骤 a) b) c) 如果训练集属于同一个类别，则创建一个叶结点，结束；否则计算训练集中每个属性划分的差异性损失，以差异性损失最大的属性为决策属性，并创结点；以第二步中的决策属性将训练集划分为两个子集，分别以这两个子集为训练集递归调用第一步。

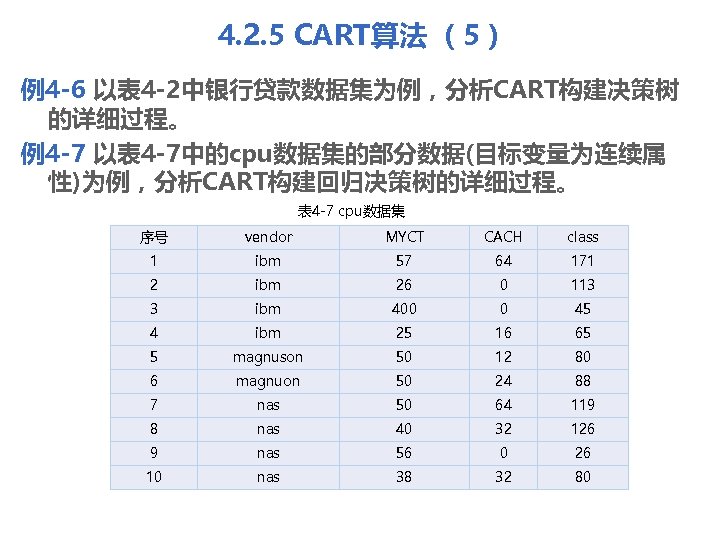
4. 2. 5 CART算法（5）例4 -6 以表 4 -2中银行贷款数据集为例，分析CART构建决策树的详细过程。例4 -7 以表 4 -7中的cpu数据集的部分数据(目标变量为连续属性)为例，分析CART构建回归决策树的详细过程。表 4 -7 cpu数据集序号 vendor MYCT CACH class 1 ibm 57 64 171 2 ibm 26 0 113 3 ibm 400 0 45 4 ibm 25 16 65 5 magnuson 50 12 80 6 magnuon 50 24 88 7 nas 50 64 119 8 nas 40 32 126 9 nas 56 0 26 10 nas 38 32 80

4. 2. 6 C 4. 5 与CART算法的区别 l C 4. 5算法和CART算法的主要区别如下： (a) C 4. 5构造的是多叉树，而CART构造的是二叉树，如果目标属性是离散型的，并且具有两个以上的类别，则CART将目标类别合并成两个超类别。 (b) C 4. 5使用信息增益率作为变量的不纯度量，而CART使用Gini系数。 (c)C 4. 5的目标变量只能是离散型，而CART中的目标变量可以是离散型也可以是数值型，如果目标变量是数值型，则CART算法找出一组基于树的回归方程来预测目标变量。 (d)对决策树的剪枝方法不同，C 4. 5通过启发式地调整在训练集样本上估计出的误差率，使用调整的误差率以找到使评分函数最大化的树。而CART采用的是代价复杂度模型，通过交叉验证来估计对测试样本集的误分类损失，产生最小交叉验证误分类估计的树。

4. 2. 7 决策树分类算法的优点 l 决策树的分类算法的具有以下优点： (1) 构造决策树的代价低； (2) 在分类未知记录时非常快； (3) 对于一些比较小的树非常容易解释； (4) 在许多简单数据集上测试发现，决策树分类技术其准确率和其它分类技术相当。

4. 3 朴素贝叶斯分类方法 4. 3. 1 朴素贝叶斯算法的相关概念 4. 3. 2 零条件概率问题的处理 4. 3. 3 朴素贝叶斯算法的优缺点

4. 3. 1 朴素贝叶斯算法的相关概念（1） l l 贝叶斯分类方法的分类原理是，利用贝叶斯公式通过对象的先验概率计算出其后验概率，即对象属于某一类的概率，选择具有最大后验概率的类作为对象所属的类。朴素贝叶斯算法的相关概念 (1)设数据集为D，其所对应的属性集为：U={A 1, A 2, …, An, C}，其中 A 1, A 2, …, An是样本的属性变量，C是有m个值C 1, C 2, . . , Cm的类标号属性变量。数据集D中的每个样本X可以表示为：X={x 1, x 2, …, xn, Ci}，描述n个属性A 1, A 2, …, An的观测值以及所属的类标号值。 (2)给定一个类标号未知的样本X，朴素贝叶斯分类将预测X属于具有最大后验概率P(Ci|X)的类(Ci是C 1, C 2, . . , Cm中的某个值)。朴素贝叶斯分类器将未知的样本X分配给类Ci当且仅当：

4. 3. 1 朴素贝叶斯算法的相关概念（2） (3)贝叶斯定理: l由于P(X)对所有类为常数，只需要最大，即最大化后验概率 P(Ci|X)可转化为最大化概率的计算。一般地，类的先验概率可以用来估计，其中是数据集D中属于类的样本个数，是数据集D 的样本总数。

4. 3. 1 朴素贝叶斯算法的相关概念（3） (4)朴素贝叶斯算法 l朴素贝叶斯算法基于各属性之间相互独立以及连续属性的条件概率服从正态分布两个假设。这样： l如果属性Ak是分类属性，则：，其中是D中 Ak的值为xk的Ci类的样本个数，是D中属于Ci类的样本个数。 l如果属性Ak是连续属性，假设服从正态分布。该分布有两个参数，均值和方差，类别Ci下属性xk的类条件概率近似为：其中和分别是数据集中属于类的样本属性Ak的平均值和方差。

4. 3. 2 零条件概率问题的处理 l l 朴素贝叶斯方法通过在全部事件中观察某事件出现的比例来估计概率，当此比例为 0时，在将来的查询中包含此事件时其概率将均为 0。为避免这一问题，条件概率为零时一般采用Laplace-估计来解决这个问题。 Laplace-估计定义如下：其中n是类中的实例总数，是类的训练样例中取值为的样例数， m是等价样本大小的参数，而p是用户指定的参数。如果没有训练集(即 n=0)，则。因此p可以看作是在类的记录中观察属性值的先验概率。等价样本大小决定先验概率p和观测概率之间的概率。其中p通常取为 1/m。

4. 3. 3 朴素贝叶斯算法的优缺点 l 朴素贝叶斯算法的优点是容易实现；面对孤立的噪声点，朴素贝叶斯分类器是健壮的；面对无关属性，该分类器是健壮的。 l 朴素贝叶斯算法的缺点是相关属性可能会降低朴素贝叶斯分类器的性能，因为对这些属性，条件独立的假设已不成立。 l 朴素贝叶斯分类假定类条件独立，即给定样本的类标号，属性的值相互条件独立。当假定成立时，与其它所有分类算法相比，朴素贝叶斯分类是最精确的。然而，在实际应用中，变量之间可能存在依赖关系，相关属性可能会降低朴素贝叶斯分类器的性能。贝叶斯信念网络(Bayesian belief network)说明联合条件的概率分布，它允许在变量的子集间定义类条件独立性。它提供一种因果关系的网络图形，这种网络也被称作信念网络、贝叶斯网络或概率网络。

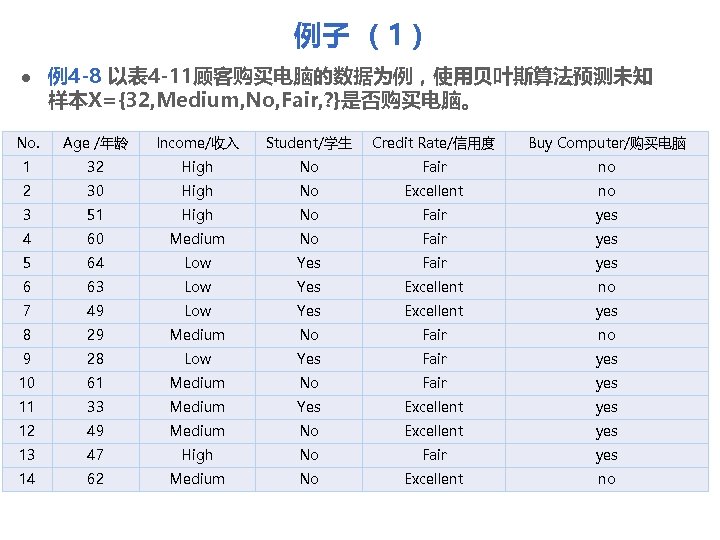
例子（1） l 例4 -8 以表 4 -11顾客购买电脑的数据为例，使用贝叶斯算法预测未知样本X={32, Medium, No, Fair, ? }是否购买电脑。 No. Age /年龄 Income/收入 Student/学生 Credit Rate/信用度 Buy Computer/购买电脑 1 32 High No Fair no 2 30 High No Excellent no 3 51 High No Fair yes 4 60 Medium No Fair yes 5 64 Low Yes Fair yes 6 63 Low Yes Excellent no 7 49 Low Yes Excellent yes 8 29 Medium No Fair no 9 28 Low Yes Fair yes 10 61 Medium No Fair yes 11 33 Medium Yes Excellent yes 12 49 Medium No Excellent yes 13 47 High No Fair yes 14 62 Medium No Excellent no

例子（3）同样方法，计算: P(购买电脑=no|X)=P(X|购买电脑=no)×P(购买电脑=no) =P(x 1|购买电脑=no)×P(x 2|购买电脑=no)×P(x 3|购买电脑=no) ×P(x 4|购买电脑=no)×P(购买电脑=no) 先计算P(x 1|购买电脑=yes)：数据集中购买电脑为no 的样本中，属性年龄的值的平均值，样本方差： P(x 3|购买电脑= no)= P(年龄=32|购买电脑= no) 计算P(x 2|购买电脑= no)： P(x 2|购买电脑= no)= P(收入=Medium|购买电脑= no)=2/5；计算P(x 3|购买电脑=yes)： P(x 3|购买电脑= no)= P(学生=No|购买电脑= no)=4/5；计算P(x 4|购买电脑=yes)： P(x 4|购买电脑= no)= P(信用度=Fair|购买电脑= no)=2/5；因此P(购买电脑= no |X)=0. 020× 2/5× 4/5× 2/5× 5/14=0. 00183；根据计算结果，P(购买电脑=yes|X) > P(购买电脑=no|X) 所以，样本X={32, Medium, No, Fair, ? }的购买电脑类标号值预测为yes。

4. 4 最近邻KNN分类方法 4. 4. 1 最近邻分类的基本概念 4. 4. 2 KNN算法描述 4. 4. 3 KNN算法优缺点 4. 4. 4 KNN的扩展

4. 4 最近邻KNN分类方法 (2) l 如果它走路象鸭子，叫声象鸭子，则它可能是一个鸭子 l 当面对新形势时，人们很自然地被过去曾经经历的类似情形的记忆所引导，这就是基于实例推理的基础。 l K最近邻（k Nearest Neighbors，简称KNN）方法正是基于这种“相似性”概念，它是一种基于已有样本进行推理的算法，通过对已有训练样本集和新进的未知样本的比较，得出与新进的未知样本最相似的K个样本，K 是用户定义的最近邻邻居样本数。最后通过对这K个样本的类标号投票得出该测试样本的类别，即如果一个样本的k个最相似的样本中的大多数属于某一个类别，则该样本也属于这个类别。

4. 4. 1 最近邻KNN分类的基本概念（1） (1)选择距离函数 l 距离是最近邻分类方法测量相似性的一个手段。对于样本的距离测量，从样本A到样本B的距离，记为d(A，B)。欧式距离是最常用的距离度量，距离测量的一般介绍见3. 2节。 (2)选择组合函数 l 距离函数用来决定哪条记录可以包含在邻居中。通过组合不同邻居的数据做出预测的方法。 (a)民主投票 l 一个通常的组合函数是由k个最近邻居投票给出一个最终的类别，每个邻居都会把票投给自己的类，从赞成每个类的票数比例可以估计新记录属于某个相应类的可能性。当任务是分配一个单一类别时，新记录就属于有最多票的那个类。 l 当只有两个类时，所选的邻居数应为奇数以避免出现平局。有一个经验法则，当有c个类时，至少要使用c+1个邻居以保证某一分类有一个相对多数。

4. 4. 1 最近邻KNN分类的基本概念（2） (b)加权投票 l 加权投票与民主投票类似，不过邻居并不是完全平等的。选票的比重与距新样本的距离成反比关系。因此，近的邻居比远的邻居有更高的比重。加权投票能够避免出现平局。 (3)选择邻居的数目 l 选择合适的K值是很重要的。如果K太小，则最近邻分类器容易受到由于训练数据中的噪声而产生的过分拟合的影响；相反，如果K太大，最近邻分类器可能会误分类测试样本，因为最近邻列表中可能包含远离其近邻的数据点。

4. 4. 2 KNN算法描述（1） l 算法步骤 (a)令K是最近邻数目，D是训练样例的集合； (b)对于每个测试样本z=(x’, y’)，计算z和D中的每个训练样例(x, y)的距离d(x’, x)； (c)选择离z最近的K个训练样例的集合Dz D； (d)样例z的类别为Dz 中出现次数最多的样本。一旦得到最近邻列表，测试样本就根据最近邻中的多数类(民主投票)进行分类： l 多数表决：其中，v是类标号，是一个最近邻的类标号，I(. )是指示函数，如果其参数为真，则返回 1，否则返回 0。

4. 4. 2 KNN算法描述（2） l 在多数表决方法中，每个近邻对分类的影响都一样，这使得算法对k的选择很敏感。降低k的影响的一种途径就是根据每个最近邻的距离不同对其作用加权：，结果使得远离z的训练样本对分类的影响要比那些靠近z的训练样本弱一些。使用距离加权表决方案，类标号可以由下面的公式确定：

4. 4. 3 KNN算法优缺点 l l KNN 算法是一种非参数化方法, 适合于概率密度函数的参数形式未知的场合。存在的缺点是： (1) 很难找到最优的K值，通常采用试探法对不同的K值进行实验以决定取哪个值较好; (2) 对大规模数据集的分类效率低。由于KNN存放所有的训练样本，不需要事先建立模型，直到有新的样本需要分类时才建立分类，因此当训练样本数量很大时，该学习算法的时间开销很大。

4. 4. 3 KNN的扩展 l u u 对KNN的改进主要从提高分类的速度和准确度两个方面进行。如先对训练样本中的每一类样本集进行聚类，然后用聚类后形成的子类代替属于该子类的所有样本集，从而大大减少了训练样本的数量，提高了分类计算速度。也可以先对未知样本集进行预分类，划分出训练集和测试集，然后采用KNN分类器进行分类，从而提高分类进度并降低时间复杂度。

例题例4 -9 以表 4 -2银行贷款数据为例，使用KNN算法预测未知样本 X=(no, married, 80 k, ? )是否拖欠贷款，其中k=3。(使用 3. 3中ksummary算法的距离公式度量邻近性)。解：第一步，计算未知样本X与第i个训练样本Pi间的距离d(X, Pi)： d(X, P 1)=1+1+45=47 d(X, P 2)=0+0+20=20 d(X, P 3)=0+1+10=11 d(X, P 4)=1+0+40=41 d(X, P 5)=0+1+15=16 d(X, P 6)=0+0+20=20 d(X, P 7)=1+1+140=142 d(X, P 8)=0+1+5=6 d(X, P 9)=0+0+5=5 d(X, P 10)=0+1+10=11 第二步，选择与X最邻近的3个训练样本，即样本 3、样本 8和样本 9。第三步，多类表决。由数据表可知，样本 3和样本 9的类别都为no，而样本 8 的类别为yes，因此样本X将划分到类别no中。

4. 5 集成分类器 4. 5. 1 构建集成分类器的过程描述 4. 5. 2 构建集成分类器的方法 4. 5. 3 集成分类器方法优缺点

4. 5. 1 构建集成分类器的过程描述（1） l 集成学习法（Ensemble learning）通过将多个分类学习方法聚集在一起来提高分类准确率和模型的稳定性。集成学习法由训练数据构建一组基分类器（base classifier），然后通过对每个基分类器的预测进行投票来实现分类。

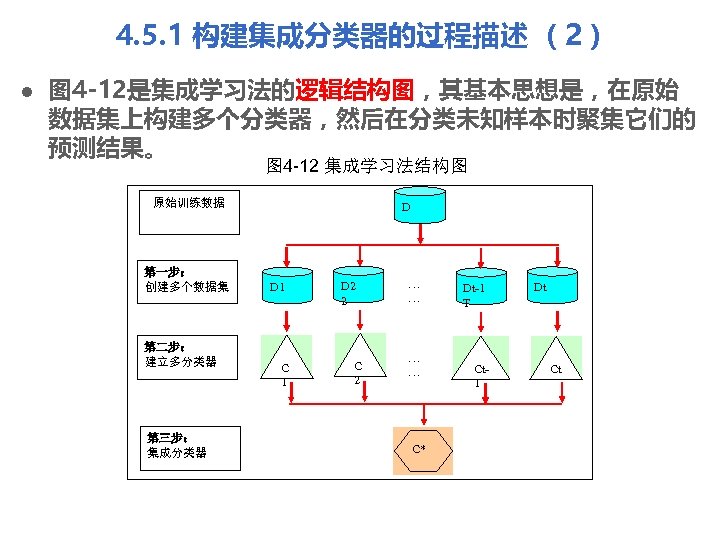
4. 5. 1 构建集成分类器的过程描述（2） l 图 4 -12是集成学习法的逻辑结构图，其基本思想是，在原始数据集上构建多个分类器，然后在分类未知样本时聚集它们的预测结果。图 4 -12 集成学习法结构图原始训练数据第一步：创建多个数据集第二步：建立多分类器第三步：集成分类器 D D 1 C 1 D 2 2 C 2 … … C* Dt-1 T- Ct 1 Dt Ct

4. 5. 1 构建集成分类器的方法（1） l l l 集成分类方法并不是简单地将数据集在多个不同分类器上重复训练，而是对数据集进行扰动，另外，一个分类训练中的错误还可以被下一个分类器利用。分类器预测错误原因之一就是未知的实例与所学习的实例的分布有所区别，通过扰动，分类器能学习到更一般的模型，从而消除单个分类器所产生的偏差，得到更为精准的模型。集成学习法(Ensemble learning)通过将多个分类学习方法聚集在一起来提高分类准确率，提高模型的稳定性。通常一个集成分类器的分类性能会好于单个分类器。集成学习法由训练数据构建一组基分类器(base classifier)，然后通过对每个基分类器的预测进行投票来实现分类。在构建分类器的过程中，一般有两种集成方法，一种是使用训练集的不同子集训练得到不同的基分类器。另一种方法是使用同一个训练集的不同属性子集训练得到不同的基分类器。

4. 5. 1 构建集成分类器的方法（2）构建集成分类器的方法如下4种： (a)通过处理训练数据集 l l 这种方法根据某种抽样分布，通过对原始数据进行再抽样来得到多个训练集然后使用特定的学习算法为每个训练集建立一个分类器。典型的处理训练数据集的组合方法有装袋(bagging)和提升(boosting)。 (b)通过处理输入特征 l 在这种方法中，通过选择输入特征的子集来形成每个训练集。一些研究表明，对那些含有大量冗余特征的数据集，这种方法的性能非常好。随机森林(Random forest)就是一种处理输入特征的组合方法。

4. 5. 1 构建集成分类器的方法（3） (c)通过处理类标号 l 这种方法适用于类数足够多的情况。通过将类标号随机划分成两个不相交的子集A 0 和A 1，把训练数据变换为二类问题。类标号属于子集A 0 的训练样本指派到类 0，而那些类标号属于子集A 1的训练样本指派到类 1。然后，使用重新标记过的数据来训练一个基分类器。重复重新标记类和构建模型步骤多次，就得到一组基分类器。当遇到一个检验样本时，使用每个基分类器Ci预测它的类标号。如果检测样本被预测为类 0，则所有属于A 0 的类都得到一票。相反，如果它被预测为类 1，则所有属于A 1 的都得到一票。最后统计选票，将检验样本指派到得票最高的类。 (d)通过处理学习算法 l 在同一个训练集上执行不同算法而得到不同的模型。

4. 5. 3 集成分类器方法优缺点 l l 集成分类器方法优点：集成分类器的应用，克服了单一分类器的诸多缺点，如对样本的敏感性，难以提高分类精度等等。集成分类器方法缺点：集成分类器的性能优于单个分类器，必须满足基分类器之间完全独立，但实践上很难保证基分类器之间完全独立。

4. 6 分类方法评价（1） l 比较不同的分类器时，需要参照的关键性能指标有： (1)分类准确率，指模型正确地预测新的或先前未见过的数据的类标号的能力。通常分类算法寻找的是分类准确率高的分类模型，分类准确率在一般情况下可以满足分类器模型的比较。 (2)计算复杂度，计算复杂度决定着算法执行的速度和占用的资源，它依赖于具体的实现细节和软硬件环境。由于数据挖掘中的操作对象是海量的数据库，因而空间和时间的复杂度将是非常重要的问题。 (3)可解释性，分类结果只有可解释性好，容易理解，才能更好地用于决策支持。结果的可解释性越好，算法受欢迎的程度越高。 (4)可伸缩性，一个模型是可伸缩的，是指在给定内存和磁盘空间等可用的系统资源的前提下，算法的运行时间应当随数据库大小线性增加。 (5)强壮性或鲁棒性，是指在数据集中含有噪声和缺失值的情况下，分类器正确分类数据的能力。

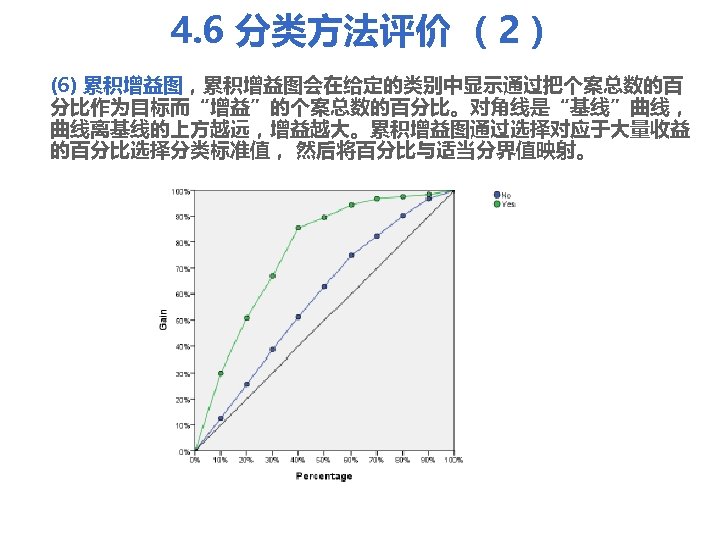
4. 6 分类方法评价（2） (6) 累积增益图，累积增益图会在给定的类别中显示通过把个案总数的百分比作为目标而“增益”的个案总数的百分比。对角线是“基线”曲线，曲线离基线的上方越远，增益越大。累积增益图通过选择对应于大量收益的百分比选择分类标准值，然后将百分比与适当分界值映射。

4. 6 分类方法评价（3） (7) 不平衡数据分类。所谓不平衡数据是指训练样本数量在类间分布不平衡，具体地说就是在同一数据集中某些类的样本数远大于其它类的样本数，其中样本少的类为少数类(以下称为正类) ，样本多的类为多数类(以下称为负类)。具有不平衡类分布的数据集出现在许多实际应用中，很多重要信息隐藏在少数类中。在不平衡数据分类中，少数类的正确分类比多数类的正确分类更有价值，仅用准确率评价分类模型并不合适。例如，如果 1%的信用卡交易是欺诈行为，则预测每个交易都合法的模型具有99%的准确率，尽管它检测不到任何欺骗交易。

4. 6 分类方法评价（4） p 表 4 -12通过混淆矩阵描述对象分类情况，在混淆矩阵中，主对角线上分别是被正确分类的正例个数(TP个)和被正确分类的负例个数(TN个)，次对角线上依次是被错误分类的负例个数(FN个)和被错误分类的正例个数 (FP个)。实际正例数(P)=TP+FN，实际负例数(N)=FP+TN，实例总数 (C)=P+N。在不平衡数据分类问题中，并不关注正确分类的负例。表 4 -12 两类问题的混合矩阵预测类别 + - + 正确的正例(TP) 错误的负例(FN) - 错误的正例(FP) 正确的负例(TN) 实际类别

4. 6 分类方法评价（5）通过上表，可以定义以下五种分类评估方法： (1)分类准确度(Accuracy)表示对测试集分类时，分类正确样本的百分比，其定义如下： l (2)错误率(Error rate)为错误分类的测试样本个数占测试样本总数的比例： (3)精度(Precision)或真负率定义为正确分类的正例个数占分类为正例的样本个数的比例：

4. 6 分类方法评价（6） (4)召回率(Recall)或真正率定义为正确分类的正例个数占实际正例个数的比例： (5) 度量, 表示精度和召回率的调和平均值：量趋向于接近精度和召回率中的较小者。，度 l精度和召回率是评价不平衡数据分类模型的两个常用度量。可以构造一个基线模型，最大化其中一个度量。例如，将每一个记录都声明为正类的模型具有完美的召回率，但它的精度却很差；相反，将匹配训练集中任何一个正记录都指派为正类的模型具有很高的精度，但召回率很低。度量可以起到平衡两个度量的效果，高的度量值确保精度和召回率都比较高。

4. 8 综合例子 l 例4 -10 银行信贷员需要能够找到预示有可能拖欠贷款的人的特征，然后使用这些特征来识别信用风险的高低。假设 850名以往客户和潜在客户的信息包含在 bankloan. sav 中。前700个个案是以前曾获得贷款的客户。将其中的700个default有值的样本拆分为训练集 (67%)和测试集(33%)，并通过多种分类方法(C 5. 0， C&R Tree，Bayes. Net，Neural. Net，SVM， Logistic)创建分类模型，而留出其余客户用于验证分析。然后使用每个模型将150名潜在客户按高或低信用风险分类。最后选择性能最好的一个模型作为该数据的分类器. 数据集的属性说明如下表所示。 age 客户年龄 ed 受教育程度 emplo y addre ss income debtin c Creddeb t 职业家庭地址家庭收入(千元) 债务收入比率信用卡债务(千元) othdebt 其它债务 default 是否违约

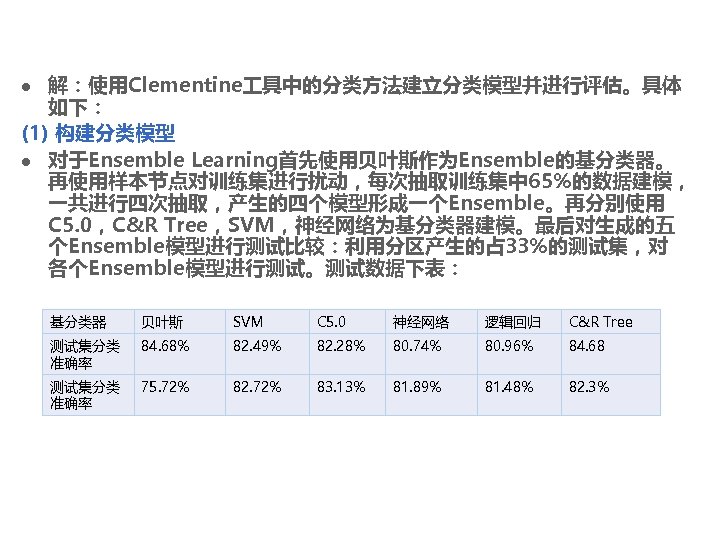
解：使用Clementine 具中的分类方法建立分类模型并进行评估。具体如下： (1) 构建分类模型 l 对于Ensemble Learning首先使用贝叶斯作为Ensemble的基分类器。再使用样本节点对训练集进行扰动，每次抽取训练集中 65%的数据建模，一共进行四次抽取，产生的四个模型形成一个Ensemble。再分别使用 C 5. 0，C&R Tree，SVM，神经网络为基分类器建模。最后对生成的五个Ensemble模型进行测试比较：利用分区产生的占 33%的测试集，对各个Ensemble模型进行测试。测试数据下表： l 基分类器贝叶斯 SVM C 5. 0 神经网络逻辑回归 C&R Tree 测试集分类准确率 84. 68% 82. 49% 82. 28% 80. 74% 80. 96% 84. 68 测试集分类准确率 75. 72% 82. 72% 83. 13% 81. 89% 81. 48% 82. 3%

根据测试结果可知，以C 5. 0作为基分类器在测试集上分类效果最好, SVM，C&R Tree, 神经网络次之。所以使用以C 5. 0作为基分类器构建的Ensemble模型。 (2) 评估模型 l Ensemble_1: 由贝叶斯网络，C 5. 0，C&R Tree，SVM，神经网络和Logistic组成的Ensemble。 l Ensemble_2: 由第一步得到的以C 5. 0为基分类器组成的 Ensemble。 l 使用测试集来评估建立的分类模型，得到如下表示结果。 l

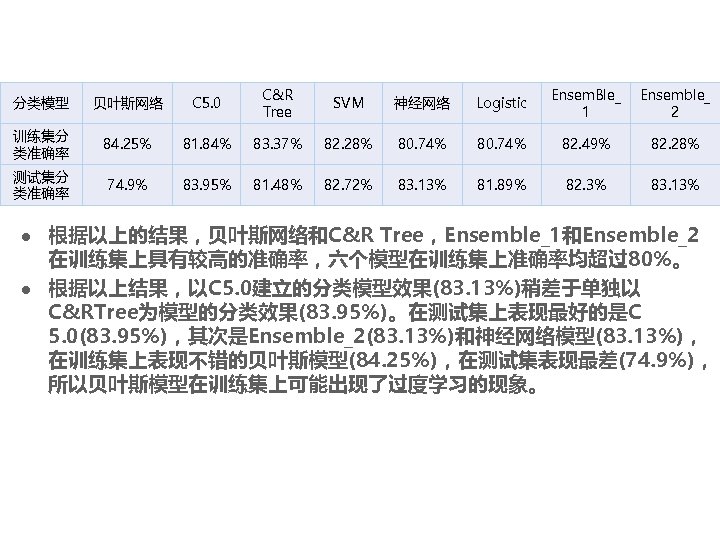
分类模型贝叶斯网络 C 5. 0 C&R Tree SVM 神经网络 Logistic Ensem. Ble_ 1 Ensemble_ 2 训练集分类准确率 84. 25% 81. 84% 83. 37% 82. 28% 80. 74% 82. 49% 82. 28% 测试集分类准确率 74. 9% 83. 95% 81. 48% 82. 72% 83. 13% 81. 89% 82. 3% 83. 13% l l 根据以上的结果，贝叶斯网络和C&R Tree，Ensemble_1和Ensemble_2 在训练集上具有较高的准确率，六个模型在训练集上准确率均超过80%。根据以上结果，以C 5. 0建立的分类模型效果(83. 13%)稍差于单独以 C&RTree为模型的分类效果(83. 95%)。在测试集上表现最好的是C 5. 0(83. 95%)，其次是Ensemble_2(83. 13%)和神经网络模型(83. 13%)，在训练集上表现不错的贝叶斯模型(84. 25%)，在测试集表现最差(74. 9%)，所以贝叶斯模型在训练集上可能出现了过度学习的现象。

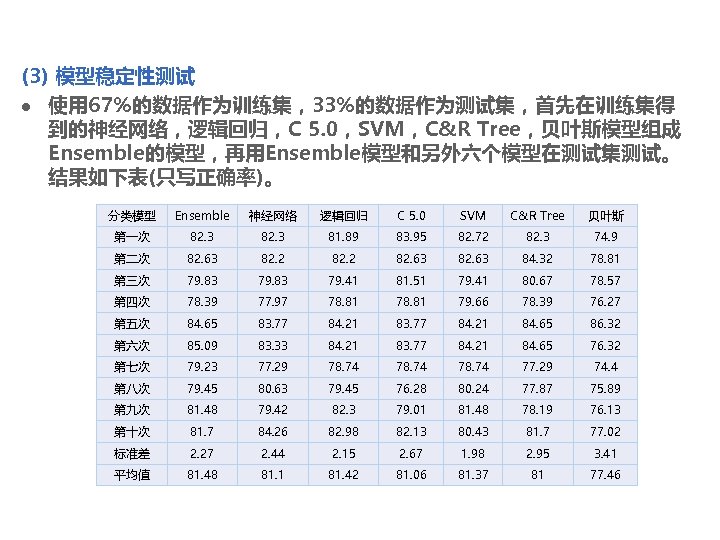
(3) 模型稳定性测试 l 使用 67%的数据作为训练集，33%的数据作为测试集，首先在训练集得到的神经网络，逻辑回归，C 5. 0，SVM，C&R Tree，贝叶斯模型组成 Ensemble的模型，再用Ensemble模型和另外六个模型在测试集测试。结果如下表(只写正确率)。分类模型 Ensemble 神经网络逻辑回归 C 5. 0 SVM C&R Tree 贝叶斯第一次 82. 3 81. 89 83. 95 82. 72 82. 3 74. 9 第二次 82. 63 82. 2 82. 63 84. 32 78. 81 第三次 79. 83 79. 41 81. 51 79. 41 80. 67 78. 57 第四次 78. 39 77. 97 78. 81 79. 66 78. 39 76. 27 第五次 84. 65 83. 77 84. 21 84. 65 86. 32 第六次 85. 09 83. 33 84. 21 83. 77 84. 21 84. 65 76. 32 第七次 79. 23 77. 29 78. 74 77. 29 74. 4 第八次 79. 45 80. 63 79. 45 76. 28 80. 24 77. 87 75. 89 第九次 81. 48 79. 42 82. 3 79. 01 81. 48 78. 19 76. 13 第十次 81. 7 84. 26 82. 98 82. 13 80. 43 81. 7 77. 02 标准差 2. 27 2. 44 2. 15 2. 67 1. 98 2. 95 3. 41 平均值 81. 48 81. 1 81. 42 81. 06 81. 37 81 77. 46

l 根据这七种分类模型在十次分类结果中的准确率计算出它们各自的平均值以及标准差。从中可以看出，以Ensemble模型， SVM模型，逻辑回归是较为稳定的三种模型。另外，贝叶斯分类模型的标准差是七种分类模型中最大的，而且十次分类的准确率平均值为七个中最小，由此可以推出贝叶斯分类模型是七种分类模型中准确率较低而且最不稳定的。

4. 9 本章小结 l l 分类是一种重要的数据挖掘技术，广泛应用于电信、金融、医学等领域中。分类的目的是对有类标号的数据集进行学习并构造一个拥有预测功能的分类模型(也常常称作分类器)，该模型能把未知类别的样本映射到给定的某一个类别中，从而实现并对未知类别的数据的预测。分类过程通常包含两个基本步骤：首先建立一个描述已知数据集类别或概念的模型；然后利用所获得的模型进行分类操作。本章对多种经典的分类方法的原理和算法过程进行详细地介绍，这些算法基于不同的分类思想，主要包括基于决策树的方法、贝叶斯方法、最近邻方法和集成分类方法，并使用样本数据说明这些分类方法的计算过程。

l 作业：P 88： 4. 1, 4. 2，4. 4