33513a9e07c62a00b179d3f94f871879.ppt
- Количество слайдов: 40

第2回 知識表現 mutty@ics. kagoshima-u. ac. jp 第2回 知識表現 1

第2回 知識表現 mutty@ics. kagoshima-u. ac. jp 知識表現の分類 -1 知識を計算機システムで利用するための記述法・枠組み 問題解決に必要な情報、特に問題領域に固有の情報 n 対象概念 - 対象物概念: 名詞 ~事実(~は~だ) - 事象概念:述語 ~part-of 、 is-a 例)part-of(roof, house), is-a-father(Sigeo, Kazushige) n n 推論知識: 事実を操作する方法 メタ知識: 知識の性質や知識の使い方 2

第2回 知識表現 mutty@ics. kagoshima-u. ac. jp 知識表現の分類 -2 n 手続き的(procedural)知識: How n 宣言的(declarative)知識: What 3

第2回 知識表現 mutty@ics. kagoshima-u. ac. jp 知識表現の分類 -3 n n 浅い(shallow)知識: 過去の問題解決に基づく経験的知識 効率○ 正当性? 柔軟性× 深い(deep)知識: 問題に関する理論的、基礎的知識 ~法則 4

第2回 知識表現 mutty@ics. kagoshima-u. ac. jp 知識表現の要件 n 表現能力の妥当性: 現実世界の知識を必要十分に表現できること n 推論の正当性: 問題解決過程において正しい推論結果を得るための操 作を行えること n 推論の効率: 組合せ爆発防止 n 知識獲得の効率: 人間が理解し易くモジュール性が高い、自動学習機構を 組込み易い、など 5

第2回 知識表現 mutty@ics. kagoshima-u. ac. jp 知識表現法の要件(2) n n n 広い知識の表現能力 ~ 構造有、不完全、知識の利用法(メタ知識) モジュール性 ~ 追加、修正、段階的発展 管理の容易さ ~ 矛盾、冗長、誤りの検出 人間にとってのわかり易さ 効率的推論との組合せ 6
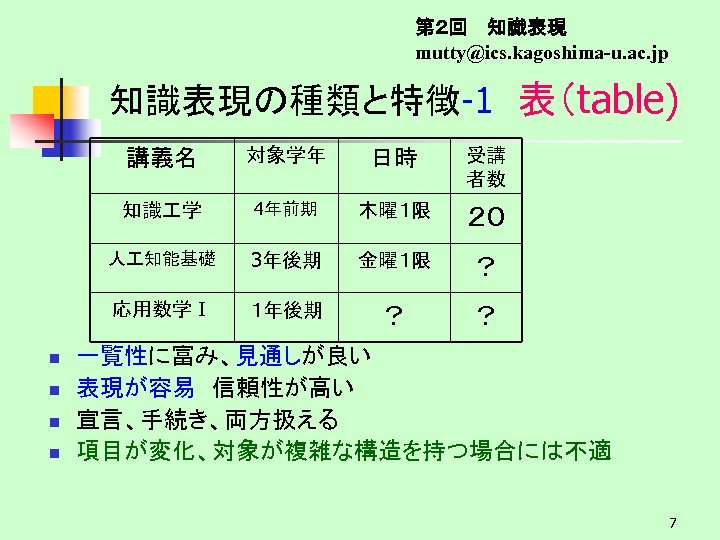
第2回 知識表現 mutty@ics. kagoshima-u. ac. jp 知識表現の種類と特徴-1 表(table) 講義名 n 4年前期 木曜1限 20 3年後期 金曜1限 ? 応用数学Ⅰ n 受講 者数 人 知能基礎 n 日時 知識 学 n 対象学年 1年後期 ? ? 一覧性に富み、見通しが良い 表現が容易 信頼性が高い 宣言、手続き、両方扱える 項目が変化、対象が複雑な構造を持つ場合には不適 7
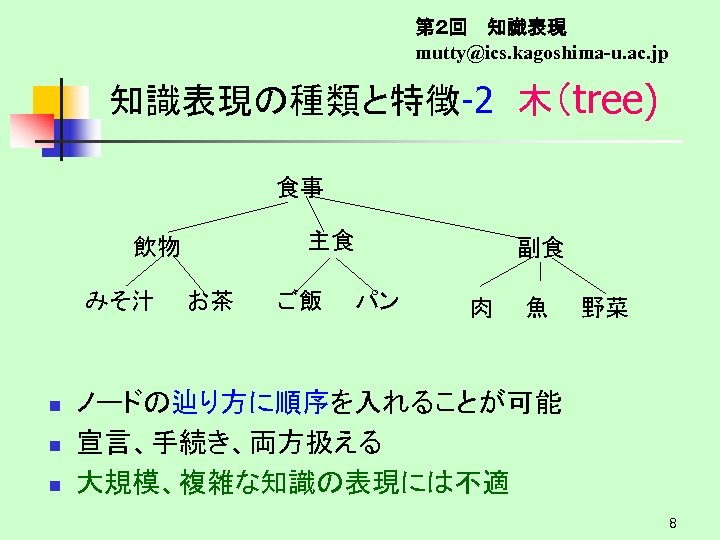
第2回 知識表現 mutty@ics. kagoshima-u. ac. jp 知識表現の種類と特徴-2 木(tree) 食事 飲物 みそ汁 お茶 n n n 主食 ご飯 パン 副食 肉 魚 野菜 ノードの辿り方に順序を入れることが可能 宣言、手続き、両方扱える 大規模、複雑な知識の表現には不適 8

第2回 知識表現 mutty@ics. kagoshima-u. ac. jp 知識表現の種類と特徴-3 数式 S=cxn+t S: 成績、c:定数、n: 出席回数、t:試験の点数 n n 表現可能な場合は非常に効率的 表現能力が限定(手続き的表現のみ) 9

第2回 知識表現 mutty@ics. kagoshima-u. ac. jp 知識表現の種類と特徴-4 プロダクション規則(production rule) ~ CMU/A.Newell (1960年代前半) IF 前提 THEN 結論または行動 n n n 前件部、条件部 後件部、結論部 複数の条件の組合せ(AND, OR)が可能 変数の導入が可能 確信度(CF: certain factor)の導入が可能 例) IF 円高が進む THEN 景気が悪くなる (CF=0.6) n 表現能力が限定(手続き的表現のみ) 10

第2回 知識表現 mutty@ics. kagoshima-u. ac. jp プロダクションシステム プロダクション規則を利用した問題解決システム n n n 単純で素人にも理解し易い モジュール性が高く、新しい知識の獲得、修正、 削除が容易 ルール間の関係が不明確 ~ 誤った結論を導いたとき、 - ルール不足か? 誤りがあったのか? - どのルールが誤りの原因か? といったことを特定するのが困難 11
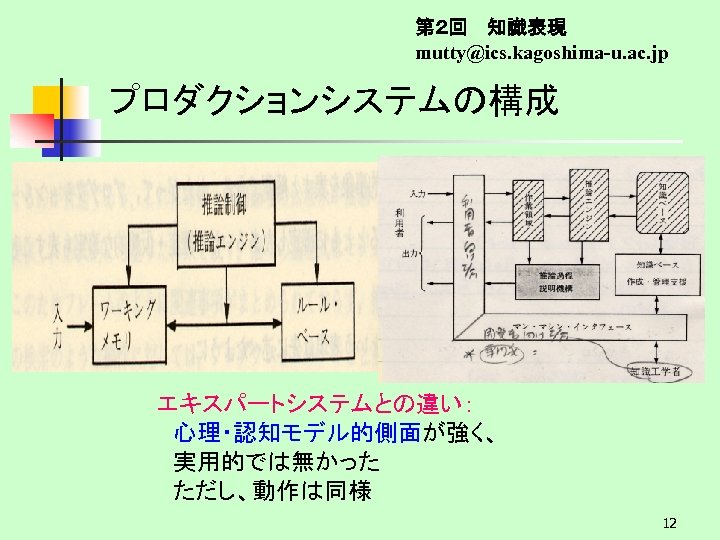
第2回 知識表現 mutty@ics. kagoshima-u. ac. jp プロダクションシステムの構成 エキスパートシステムとの違い: 心理・認知モデル的側面が強く、 実用的では無かった ただし、動作は同様 12

第2回 知識表現 mutty@ics. kagoshima-u. ac. jp 知識表現の種類と特徴-5 意味ネットワーク(semantic network) ~ R.Quillian (1967年) オブジェクト(物、事柄、概念)をノード、オブジェ クト間の関係・属性をアークとする有向グラフ構 造 n n 直感性に優れ、ネットワークを辿ることによる知 識の獲得が容易(継承) 機能の異なる記述(階層構造、動作、・・)が混在 → 推論処理が複雑 13
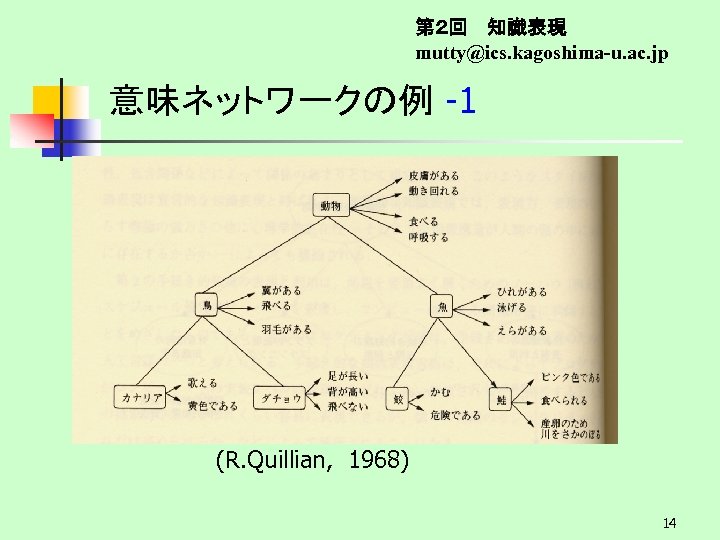
第2回 知識表現 mutty@ics. kagoshima-u. ac. jp 意味ネットワークの例 -1 (R. Quillian, 1968) 14
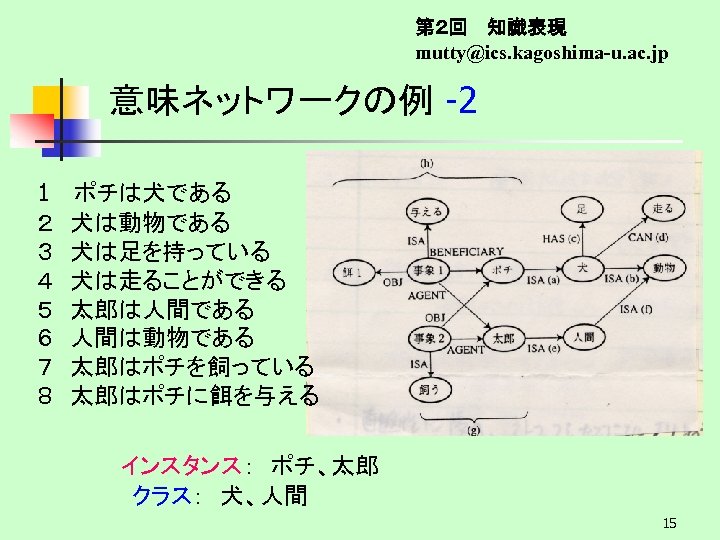
第2回 知識表現 mutty@ics. kagoshima-u. ac. jp 意味ネットワークの例 -2 1 ポチは犬である 2 犬は動物である 3 犬は足を持っている 4 犬は走ることができる 5 太郎は人間である 6 人間は動物である 7 太郎はポチを飼っている 8 太郎はポチに餌を与える インスタンス: ポチ、太郎 クラス: 犬、人間 15

第2回 知識表現 mutty@ics. kagoshima-u. ac. jp 意味ネットワークの特色 n n n 関係性を重視 vs プロダクション規則 2項関係で記述 - Is-a 関係: 継承機能付与 ~ 冗長性排除、整合性保持 - has-a 関係: 継承機能無し 図的表示による知識の表現 vs 自然言語理解における 概念依存構造(Schunck) 16
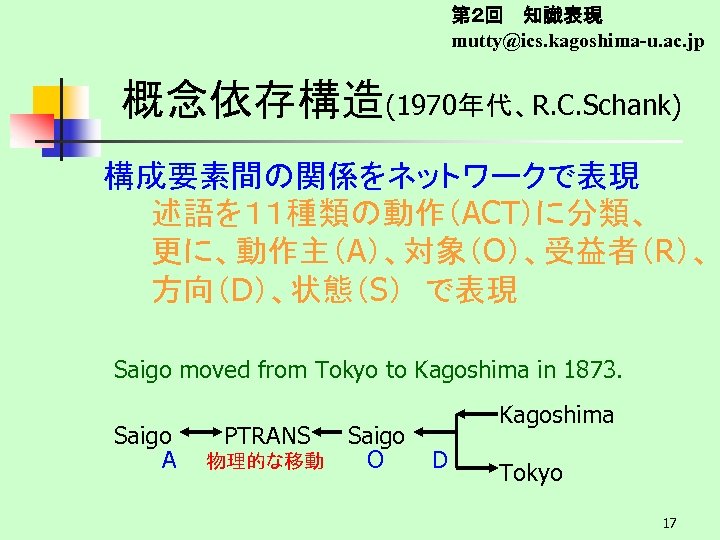
第2回 知識表現 mutty@ics. kagoshima-u. ac. jp 概念依存構造(1970年代、R. C. Schank) 構成要素間の関係をネットワークで表現 述語を11種類の動作(ACT)に分類、 更に、動作主(A)、対象(O)、受益者(R)、 方向(D)、状態(S) で表現 Saigo moved from Tokyo to Kagoshima in 1873. Saigo A PTRANS Saigo 物理的な移動 O D Kagoshima Tokyo 17

第2回 知識表現 mutty@ics. kagoshima-u. ac. jp 知識表現の種類と特徴 -6 フレーム(frame) ~ MIT・M.Minsky “A Framework for Representing Knowledge” (1975年) 「人 知能や心理学で扱う基本単位は、概してあ まりにも小さく局所的で非構造的なため、人間の 常識的思考の効率の良さを説明する役には立た ない。・・・・・フレームとは、居室にいるとか、子供 の誕生パーティに行くとかいうような、型に嵌った 状況を表現するためのデータ構造である。・・」 18

第2回 知識表現 mutty@ics. kagoshima-u. ac. jp フレームの構造と意味ネットワークとの違い n n ファセットを用いて、値の種類を明示的に定められる ~ VALUE(通常値), REQUIRE(制約), DEFAULT(暗黙値) スロットの値として、手続きを埋め込める ~ IF-Needed(値の導出時に起動), IF-Added(値の追加時に起動 ). . 19

第2回 知識表現 mutty@ics. kagoshima-u. ac. jp フレームの特徴 n 強力な表現能力 n モジュール性が低い ~ 手続きがフレーム内に埋め込まれている ため、推論過程と知識が一体化している → 獲得・修正が困難 20

第2回 知識表現 mutty@ics. kagoshima-u. ac. jp 知識表現の種類と特徴-7 述語論理(predicate calculus, logic) 知識を記号の式として数学的に表現 cf)述語: 真偽判定可能な叙述 例) (∀X)(elephant(X) → color(X, gray)) n n n 理論的基盤が保証されている 導出原理(resolution principle)による推論 人間の持つ曖昧性を組み込むことが困難 21

第9回 一階述語論理 mutty@ics. kagoshima-u. ac. jp 命題論理の限界 個体への言及不可 ~記述の最小単位:命題 例)・p: 「全ての日本人は人間」 ・q: 「太郎は日本人」 → r: 「太郎は人間」 が導出できない ~ (p∧q)→rは恒真命題でない n 22
![第9回 一階述語論理 mutty@ics. kagoshima-u. ac. jp 命題論理の述語論理への拡張 個体に注目し,「個体について何が述べられてい るか」という観点から命題の内部構造を記述 対象領域: 議論の対象となる個体の集合 ・∀x[J(x)→M(x)] ・J(a) a: 第9回 一階述語論理 mutty@ics. kagoshima-u. ac. jp 命題論理の述語論理への拡張 個体に注目し,「個体について何が述べられてい るか」という観点から命題の内部構造を記述 対象領域: 議論の対象となる個体の集合 ・∀x[J(x)→M(x)] ・J(a) a:](https://present5.com/presentation/33513a9e07c62a00b179d3f94f871879/image-23.jpg)
第9回 一階述語論理 mutty@ics. kagoshima-u. ac. jp 命題論理の述語論理への拡張 個体に注目し,「個体について何が述べられてい るか」という観点から命題の内部構造を記述 対象領域: 議論の対象となる個体の集合 ・∀x[J(x)→M(x)] ・J(a) a: 太郎 n → M(a) 一階述語論理: 個体についてのみ変数を認める述語論理 ~ 完全な演繹体系 α|=β → α|-β 23

述語論理表現に用いる記号 n n n 定数 変数 関数記号: plus(X, Y) 述語記号: red(X)、study(x, school, English) 論理結合子: -連言(conjunction): ∧ 選言(disjunction): ∨ -否定(negation): ¬ 含意(implication): → 束縛(量)記号: -全称記号: ∀ 存在記号: ∃ 24

不確実な事実・知識の表現法 例外(非単調性)に起因する不確実性: - 閉世界仮説に基づくサーカムスクリプション - デフォルト推論(様相非単調論理) n 曖昧さに起因する不確実性: - 信頼性係数(CF:Certainty Factor) - ファジィ理論 - ベイズ確率 - Dempster-Shafer(DS)理論 n 25

第11回 信念管理(2) mutty@ics. kagoshima-u. ac. jp 閉世界仮説(closed world assumption) P(x)が証明できなければ~P(x)は真とする ~ 与えられた情報が世界の全てで,それ以上 の情報が後から新たに得られることはない (真であることは全て言及されている) ●実世界では不成立、人間の通常の推論過程 知識ベースに含まれていないことは偽 (書かれていない知識は否定される) 26
![第11回 信念管理(2) mutty@ics. kagoshima-u. ac. jp サーカムスクリプション(極小限定) 述語P(x)に関する命題A(P)が成立している場合, Pを全て任意の述語φで置き換えた論理式をA(φ) とすると,Pのサーカムスクリプション: A(φ)∧(∀x)[φ(x) → P(x)] → (∀x) 第11回 信念管理(2) mutty@ics. kagoshima-u. ac. jp サーカムスクリプション(極小限定) 述語P(x)に関する命題A(P)が成立している場合, Pを全て任意の述語φで置き換えた論理式をA(φ) とすると,Pのサーカムスクリプション: A(φ)∧(∀x)[φ(x) → P(x)] → (∀x)](https://present5.com/presentation/33513a9e07c62a00b179d3f94f871879/image-27.jpg)
第11回 信念管理(2) mutty@ics. kagoshima-u. ac. jp サーカムスクリプション(極小限定) 述語P(x)に関する命題A(P)が成立している場合, Pを全て任意の述語φで置き換えた論理式をA(φ) とすると,Pのサーカムスクリプション: A(φ)∧(∀x)[φ(x) → P(x)] → (∀x) [P(x) →φ(x)] ~命題Aを満足するものは述語Pのみ(制限) 考慮する対象はそこに述べられているものだけに言及す る(推論規則) 27
![第11回 信念管理(2) mutty@ics. kagoshima-u. ac. jp 閉世界仮説とサーカムスクリプションの例 P≡BLOCK: (∀x)[BLOCK(x)→(x=a∨x=b∨x=c)]: 閉世界仮説 A(φ)∧(∀x)[φ(x) → BLOCK(x)] → (∀x) 第11回 信念管理(2) mutty@ics. kagoshima-u. ac. jp 閉世界仮説とサーカムスクリプションの例 P≡BLOCK: (∀x)[BLOCK(x)→(x=a∨x=b∨x=c)]: 閉世界仮説 A(φ)∧(∀x)[φ(x) → BLOCK(x)] → (∀x)](https://present5.com/presentation/33513a9e07c62a00b179d3f94f871879/image-28.jpg)
第11回 信念管理(2) mutty@ics. kagoshima-u. ac. jp 閉世界仮説とサーカムスクリプションの例 P≡BLOCK: (∀x)[BLOCK(x)→(x=a∨x=b∨x=c)]: 閉世界仮説 A(φ)∧(∀x)[φ(x) → BLOCK(x)] → (∀x) [BLOCK(x) →φ(x)] ここでφ(x) ≡ (x=a ∨x=b ∨ x=c)とすれば、 (∀x)[(x=a ∨x=b ∨ x=c) → BLOCK(x)] → (∀x)→[BLOCK(x)(x=a ∨x=b ∨ x=c)] φ(x)≡RED (x)とすれば、 [RED(a)∧RED(b)∧RED(c)] ∧(∀x)[RED(x) →(∀x) [BLOCK(x) →RED(x)] → BLOCK(x)] 28

第11回 信念管理(2) mutty@ics. kagoshima-u. ac. jp 様相非単調論理 命題p,様相オペレータMから 信念Mpを生成: 「pであると信じることは,自分が持っている 他の信念と矛盾しない」 例) (∀x)[鳥(x) ∧M飛ぶ(x) → 飛ぶ(x)] ~ 任意の鳥xについて,xが飛ぶと仮定して 矛盾が生じない限り,xは飛ぶ 29

第11回 信念管理(2) mutty@ics. kagoshima-u. ac. jp 様相記号を用いた知識表現 Pが成立ち、~Qが証明されていなければ、 Rが成立つ; P:MQ R P:前提 Q:仮定 R:帰結 M:様相記号 正規デフォルト規則(Q=R): P:MQ Q 拡張: 公理系に推論規則を適用することにより 論理式の集合(定理群)を得ること - 多重拡張 ~ 拡張結果が複数通り出現 - 演繹結果が規則の適用順序に依存 30

第11回 信念管理(2) mutty@ics. kagoshima-u. ac. jp 様相記号を用いた知識表現の例 閉世界仮説: :M~P ~P ~(~P)=P 恒温動物(x) ∧~飛ぶ(x):M哺乳類(x) 31

第1 2回 不確実性の取り扱い mutty@ics. kagoshima-u. ac. jp 信頼性係数 n n n 血液感染症診断支援・MYCINで最初に導 入 後向き推論の効率化に有効 理論的裏付けに乏しい 32

第1 2回 不確実性の取り扱い mutty@ics. kagoshima-u. ac. jp 信頼性係数:MYCINにおける知識の例 n n 事実型: ・培養基の場所は血液である(1. 0) ・培養基の菌は好気性である(0. 25) ・培養基の菌は大腸菌である(0. 75) (): 確信度 プロダクションルール型: もし 感染症の種類が一次敗血症であり、 培養基の場所が無菌の場所であり、 培養された菌の入口が胃腸管と推定される ならば、 その菌はバクテロイドである兆候がある(0. 7) 33

第1 2回 不確実性の取り扱い mutty@ics. kagoshima-u. ac. jp ファジイ理論 n 米・L. A. Zadehが提案 (1965) 確からしさを 0~1の実数値で表現:主観 n membership(所属度)関数による連続表現 n μ(f(x)∧g(y))=min{μ(f(x)), μ(g(y)) } μ(f(x)∨g(y))=max{μ(f(x)), μ(g(y)) } 34

第1 2回 不確実性の取り扱い mutty@ics. kagoshima-u. ac. jp ベイズネットワーク ベイズの定理に基づく不確実な情報の表現 確率変数間の依存関係に関する知識を グラフとして保持・更新 ・ノード: 確率変数 ・アーク: ノード間の因果関係の存在 35

第1 2回 不確実性の取り扱い mutty@ics. kagoshima-u. ac. jp ベイズの定理 Fi が互いに独立(素),かつ F 1∪F2 ∪・・ ∪Fk= Ω P(E) = P(E/F 1)P(F 1)+ P(E/F2)P(F2) +・・・ + P(E/Fk)P(Fk) ベイズの定理: P(Fi/E) = P(E/Fi)・P(Fi) / P(E) = P(E/Fi)・P(Fi) / {P(E/F 1)P(F 1)+ P(E/F2)P(F2) +・・・+ P(E/Fk)P(Fk) } 36

第1 2回 不確実性の取り扱い mutty@ics. kagoshima-u. ac. jp ベイジアンネットの性質 n n n ネットワークにおける全ての変数に対し,その親 に条件付けされた各ノードの結合確率を規定す るだけでOK 以上で規定された条件付き確率は大域的に無矛 盾であることが保証 各ノードにおける条件付き確率の集合は ネットワークにおける全てのノードの唯一の結合 確率分布を規定 確率変数:{真,偽} 37
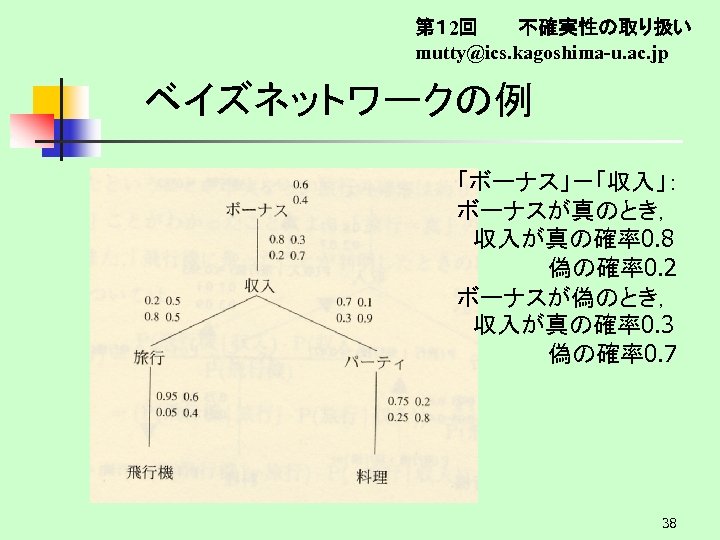
第1 2回 不確実性の取り扱い mutty@ics. kagoshima-u. ac. jp ベイズネットワークの例 「ボーナス」-「収入」: ボーナスが真のとき, 収入が真の確率0. 8 偽の確率0. 2 ボーナスが偽のとき, 収入が真の確率0. 3 偽の確率0. 7 38

第1 2回 不確実性の取り扱い mutty@ics. kagoshima-u. ac. jp Dempster-Shafer理論 n ベイズの枠組みでは以下の事象の区別が不能 (1)X=aと予想できる強い根拠があるが, X=bと予想できる同様の強い根拠がある (2) X≠aと予想できる強い根拠があるが, X ≠ bと予想できる同様の強い根拠がある (3)X=aまたはbであるか皆目わからない ⇒ 事前確率:P(a) = P(b) = 0. 5 n 無知量を表現できるよう,ベイズの枠組みを拡張 39

画像・映像における知識表現 n n n パターン自体: 抽出・蓄積が容易 vs 冗長,本質的? パターンから抽出された特徴: パターン自体よりは本質的 vs 特徴の選択,抽出法? 記号表現: 従来の知識処理との親和性大 vs 情報の大幅欠落 40
33513a9e07c62a00b179d3f94f871879.ppt