圓的弦線 A 圓的弦線定理1 p 124 由圓心至弦的垂必平分該弦

Зарегистрируйтесь, чтобы просмотреть полный документ!

РЕГИСТРАЦИЯ

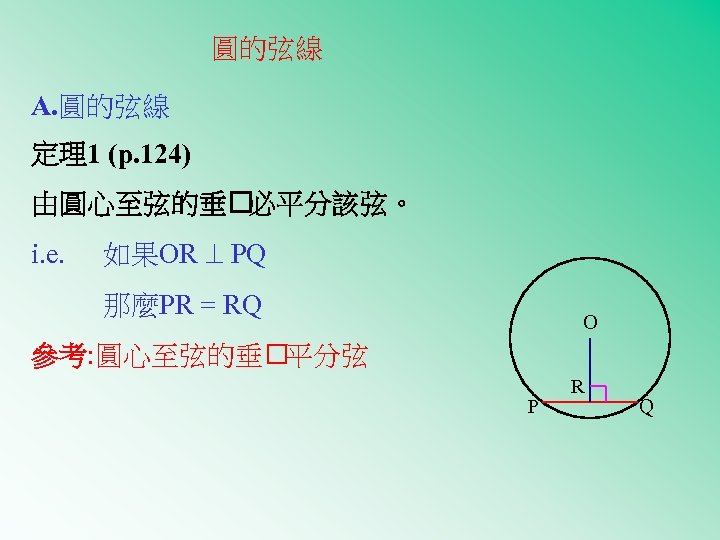
圓的弦線 A. 圓的弦線定理1 (p. 124) 由圓心至弦的垂必平分該弦。 i. e. 如果OR PQ 那麼PR = RQ O 參考: 圓心至弦的垂平分弦 P R Q

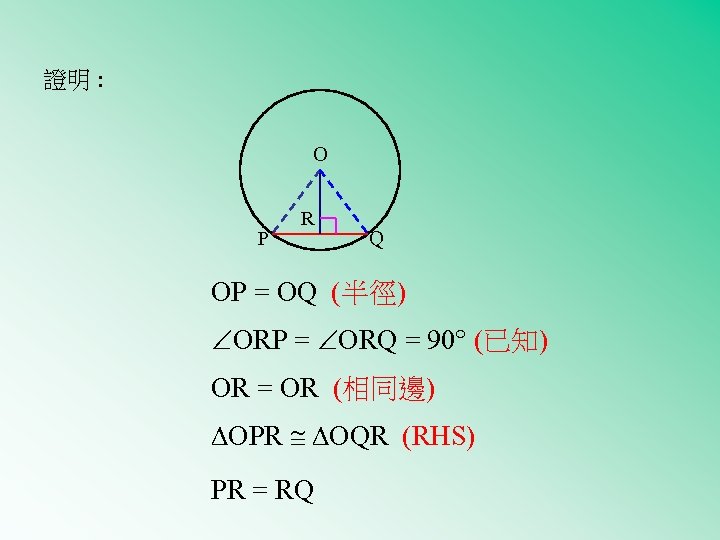
證明 : O P R Q OP = OQ (半徑) ORP = ORQ = 90 (已知) OR = OR (相同邊) OPR OQR (RHS) PR = RQ

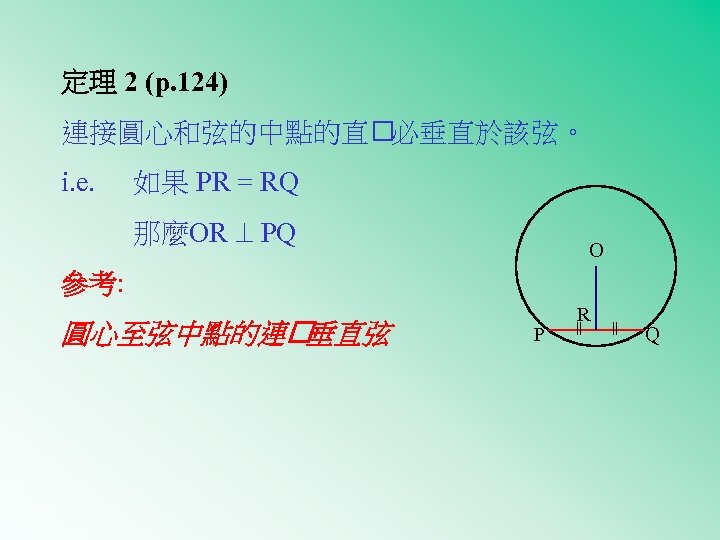
定理 2 (p. 124) 連接圓心和弦的中點的直必垂直於該弦。 i. e. 如果 PR = RQ 那麼OR PQ O 參考: P = = 圓心至弦中點的連垂直弦 R Q

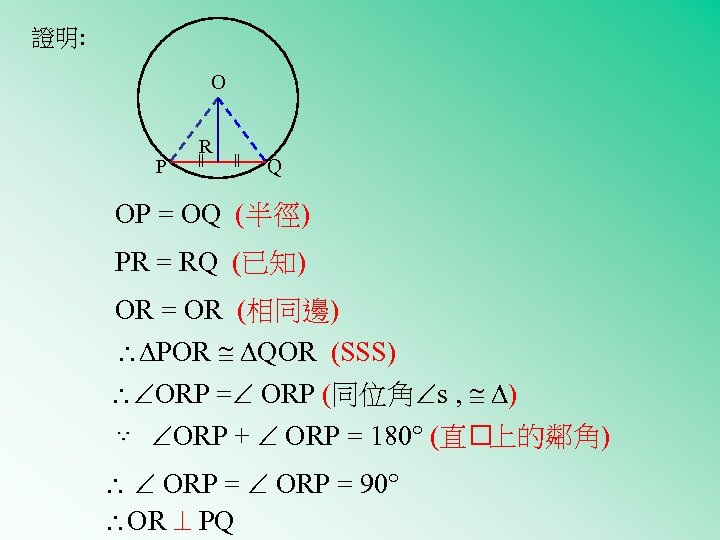
證明: O = = P R Q OP = OQ (半徑) PR = RQ (已知) OR = OR (相同邊) POR QOR (SSS) ORP = ORP (同位角 s , ) ORP + ORP = 180 (直上的鄰角) ORP = 90 OR PQ

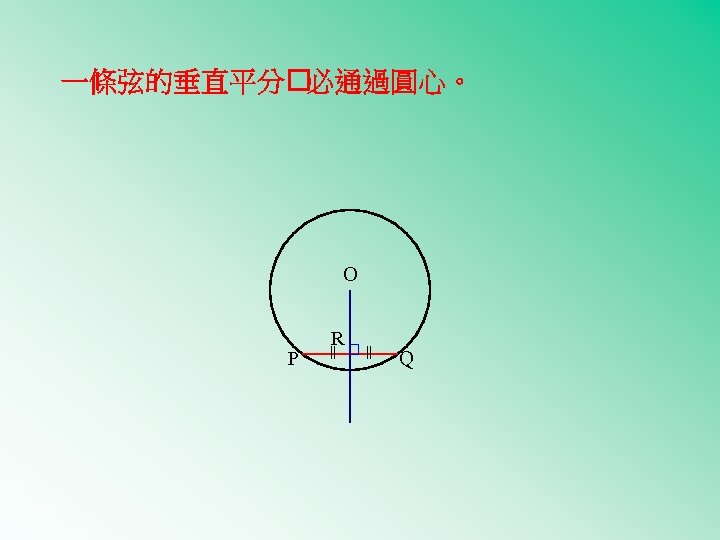
一條弦的垂直平分必通過圓心。 O = = P R Q

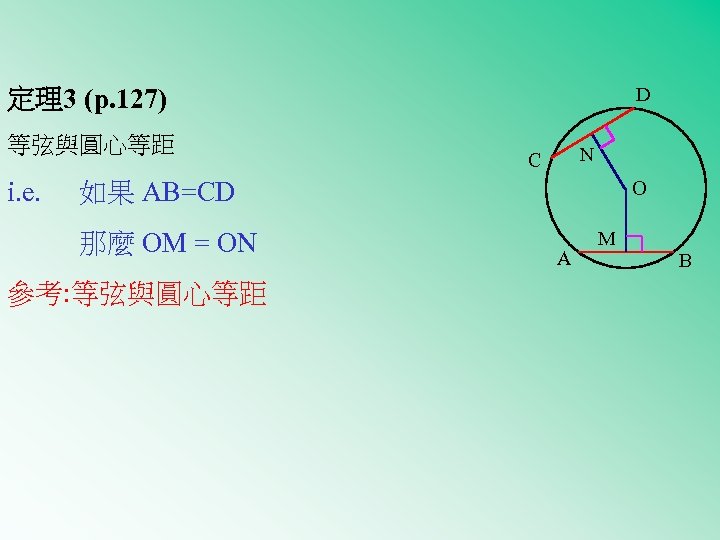
定理3 (p. 127) 等弦與圓心等距 i. e. D N C 如果 AB=CD 那麼 OM = ON 參考: 等弦與圓心等距 O A M B

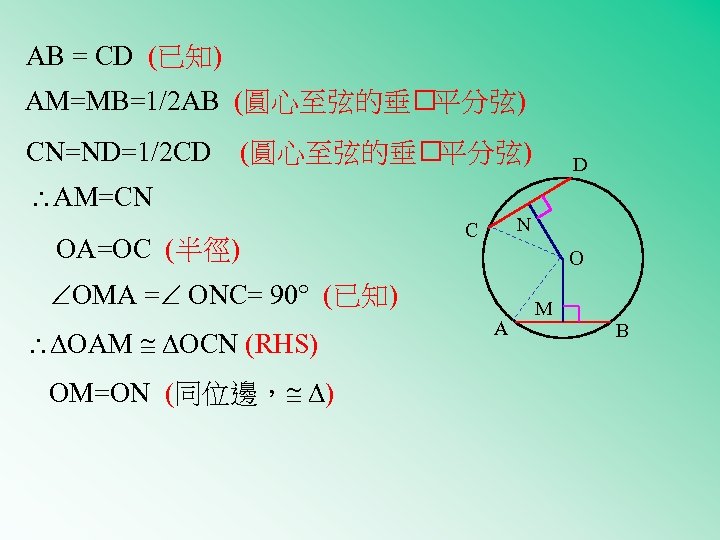
AB = CD (已知) AM=MB=1/2 AB (圓心至弦的垂平分弦) CN=ND=1/2 CD (圓心至弦的垂平分弦) D AM=CN OA=OC (半徑) N C O OMA = ONC= 90 (已知) OAM OCN (RHS) OM=ON (同位邊， ) A M B

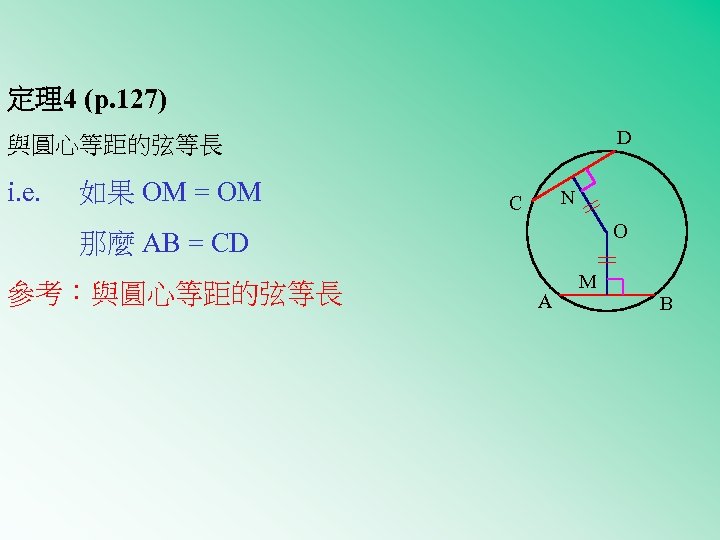
定理4 (p. 127) D 與圓心等距的弦等長 i. e. 如果 OM = OM N C O 那麼 AB = CD 參考：與圓心等距的弦等長 A M B

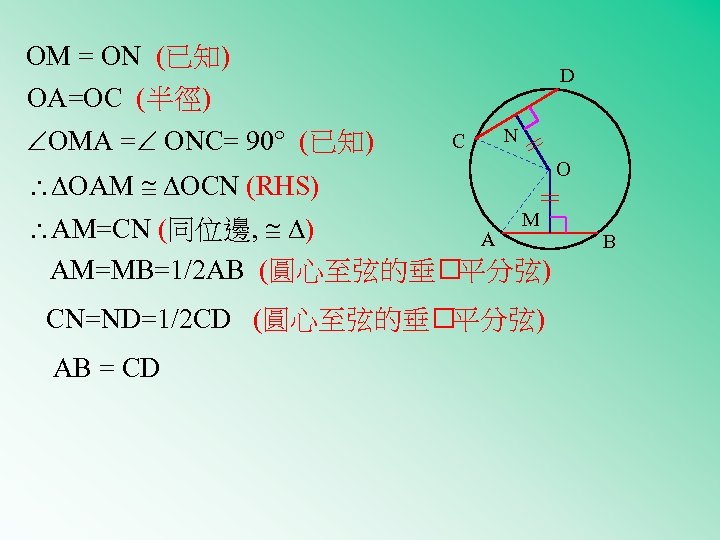
OM = ON (已知) D OA=OC (半徑) OMA = ONC= 90 (已知) C N OAM OCN (RHS) M AM=CN (同位邊, ) A AM=MB=1/2 AB (圓心至弦的垂平分弦) CN=ND=1/2 CD (圓心至弦的垂平分弦) AB = CD O B

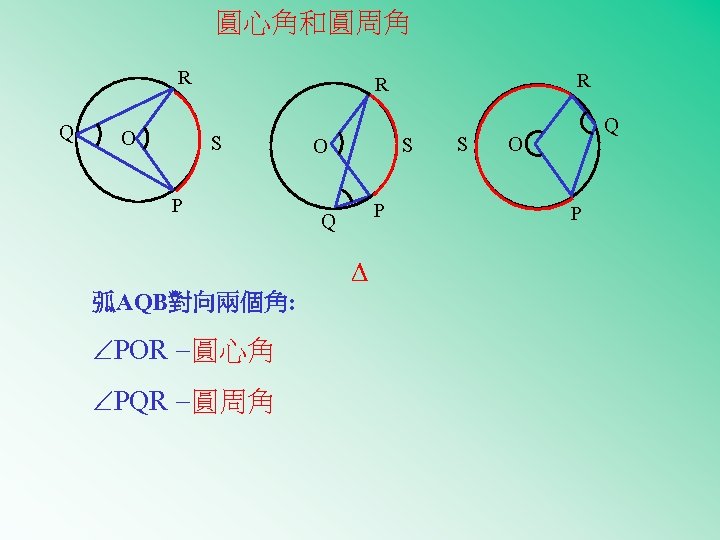
圓心角和圓周角 R Q O R R S P S O P Q 弧AQB對向兩個角: POR -圓心角 PQR -圓周角 S Q O P

定理 5 (p. 132) 圓心角兩倍於圓周角 i. e. 2 a = b 參考圓心角兩倍於圓周角 R Q a. O b S P

OQ = OR (半徑) OQR = ORQ = x (等腰底角) m =2 x ( 外角) 相似地, n = 2 y a = n+ m = 2 x +2 y = 2 b POR = 2 PQR R Q x. O m y n P

OQ = OR (半徑) OQR = ORQ = x (等腰內角) m =2 x ( 外角) 相似地, n = 2 y a = n+ m = 2 x +2 y = 2 b POR = 2 PQR R S m O n x y P Q

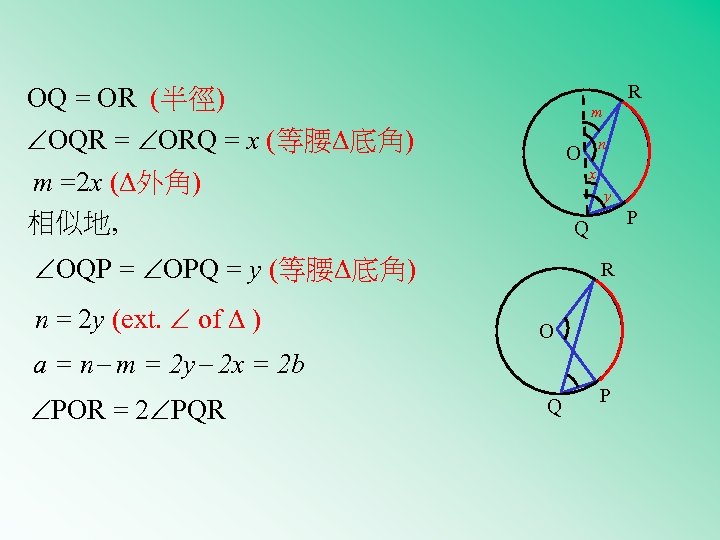
R OQ = OR (半徑) m OQR = ORQ = x (等腰底角) m =2 x ( 外角) 相似地, x y P Q OQP = OPQ = y (等腰底角) n = 2 y (ext. of ) n O R O a = n- m = 2 y- 2 x = 2 b POR = 2 PQR Q P

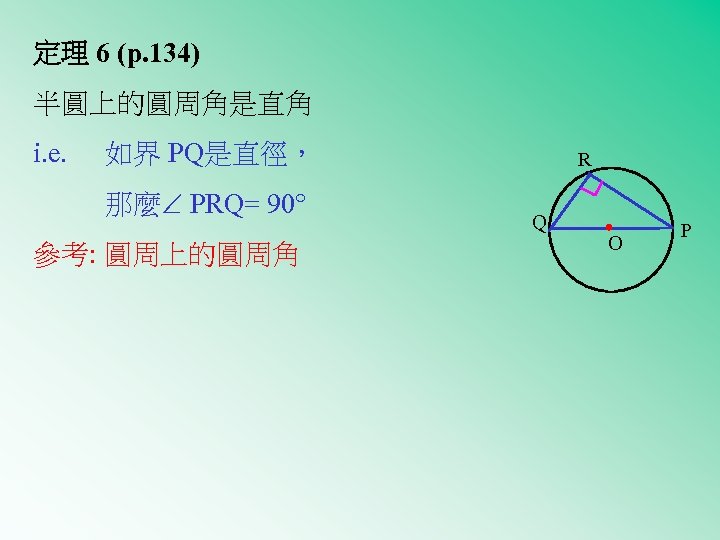
定理 6 (p. 134) 半圓上的圓周角是直角 i. e. 如界 PQ是直徑，那麼 PRQ= 90 參考: 圓周上的圓周角 R Q O P

C x A 陰影部份ACB -主要弓形 x -弓形ACB上的角 x , y -在同一弓形上的角 y B

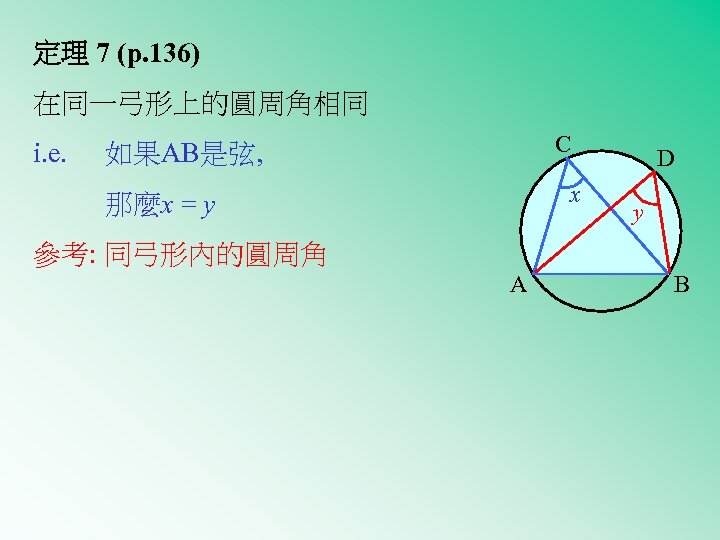
定理 7 (p. 136) 在同一弓形上的圓周角相同 i. e. C 如果AB是弦, x 那麼x = y D y 參考: 同弓形內的圓周角 A B

Скачать презентацию 圓的弦線 A 圓的弦線定理1 p 124 由圓心至弦的垂必平分該弦

088a1d4ea7aac2f6802b8234175c6d6f.ppt

Количество слайдов: 17

圓的弦線 A 圓的弦線 定理1 p 124 由圓心至弦的垂 必平分該弦

圓的弦線 A 圓的弦線定理1 p 124 由圓心至弦的垂必平分該弦