• ДИСКРЕТНАЯ МАТЕМАТИКА • Регулярные

• ДИСКРЕТНАЯ МАТЕМАТИКА

• Регулярные языки и конечные автоматы

• Множество всех слов, распознаваемых автоматом, мы назвали языком.

Автоматный язык • Грамматика типа 3 – имеют правила вида А a. B, либо A b, где А, В N; a, b T. • Здесь A, B, a, b – одиночные символы (не цепочки) соответствующих словарей. • A, B - состояния автомата, a, b - входные символы

. • Суммой языков L и L´ называется язык, который обозначается L + L´ и получается объединением множеств L и L´, т. е. • L + L´ = • Сумма языков состоит из слов, принадлежащих хотя бы одному из языков L и L´. Поэтому L + L´ = L´ + L.

. • Далее конкатенацией (или соединением) слов w и w´ будем называть слово ww´, полученное приписываем справа слова w´ к слову w. • Например, конкатенацией слов ba и cba будет слово bacba. • Из этих же слов можно получить слово cbaba, которое является конкатенацией cba и ba. • В общем случае конкатенации ww´ и w´w различаются.

• Произведением языков L и L´ называется язык, который обозначается L·L´ и получается в результате конкатенации всех возможных слов w и w´, где w принадлежит языку L, а w´ – языку L´, • Пример 1. Пусть L = {a, cb}, L´ = {ab, bсb}. Тогда • L·L´ = {aab, abcb, cbab, cbbcb}, • L´·L = {aba, abcb, bcba, bcbcb}. • Слово abcb принадлежит обоим языкам L·L´ и L´·L.

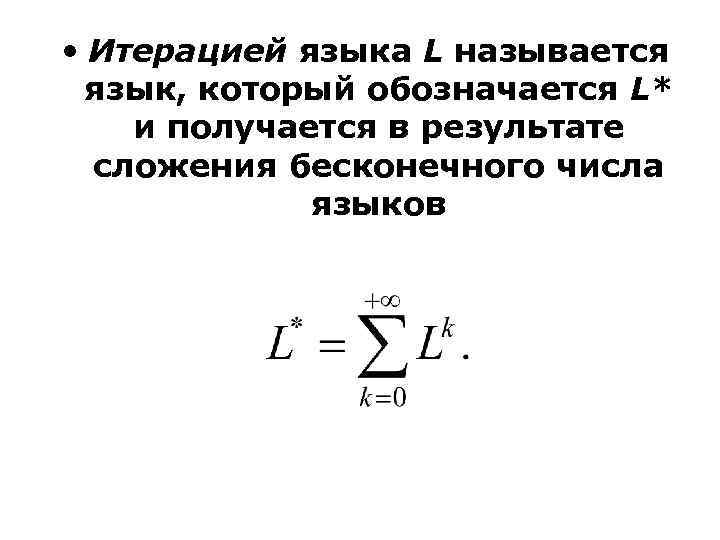• Итерацией языка L называется язык, который обозначается L* и получается в результате сложения бесконечного числа языков

• Пусть имеется алфавит • А = {а 1, а 2, …, аs}. Одноэлементные языки а 1, а 2, …, аs, а также язык, содержащий только пустое слово Λ, будем называть элементарными языками.

• Регулярным языком называется такой язык, который можно получить из элементарных языков с помощью конечного числа операций сложения, умножения и итерации.

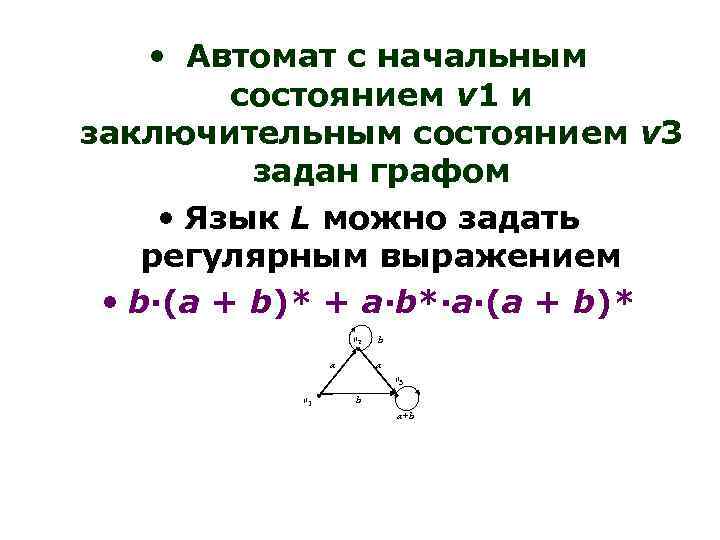• Автомат с начальным состоянием v 1 и заключительным состоянием v 3 задан графом • Язык L можно задать регулярным выражением • b·(a + b)* + a·b*·а·(a + b)* v 2 b a a v 3 v 1 b a+b

• ТЕОРЕМА КЛИНИ (основная теорема теории автоматов). • Язык L распознается конечным детерминированным автоматом тогда и только тогда, когда L – регулярный язык.

Stephen C Kleene-19091994. США.

Хомский, Аврам Ноам

• Это теоретическая основа многих информационных технологий, таких как разработка математического обеспечения вычислительных систем, проектирование компиляторов и синтаксических анализаторов для языков программирования, создание лингвистических структур для баз данных и знаний

• 3. Коллективы автоматов

• Коллективы автоматов - множество взаимодействующих для решения общей задачи автоматов.

• Системы распределенной обработки информации представляют собой воплощение идеи создания так называемых однородных сред (клеточных автоматов), предложенных в 60 е годы 20 века. • Предполагалось в начале, что элементы таких сред - элементарные конечные автоматы.

Эта область связана с именем М. Л. Цетлина. Михаил Львович Цетлин ( 1924 — 1966)

32 -битный транспьютерный чип IMST 414 B (1989)

Клеточный автомат • (КА) — набор клеток, образующих некоторую периодическую решетку с заданными правилами перехода, определяющими состояние клетки в следующий момент времени через состояние клеток, находящимися от нее на расстоянии не больше некоторого, в текущий момент времени.

Клеточный автомат • Как правило, рассматриваются автоматы, где состояние определяется самой клеткой и ближайшими соседями. • В качестве решетки обычно рассматривается кубическая решетка. • Один из самых интересных примеров клеточного автомата — игра «Жизнь» .

«Жизнь»

• Каждая клетка может находиться в двух состояниях: быть живой или быть мёртвой. • Клетка имеет восемь соседей. • Распределение живых клеток в начале игры называется первым поколением.

• Каждое следующее поколение рассчитывается на основе предыдущего по таким правилам: • пустая (мёртвая) клетка ровно с тремя живыми клетками-соседями оживает; • если у живой клетки есть две или три живые соседки, то эта клетка продолжает жить; • в противном случае (если соседок меньше двух или больше трёх) клетка умирает (от «одиночества» или от «перенаселённости» ).

• Игрок не принимает прямого участия в игре, а лишь расставляет «живые» клетки, которые взаимодействуют согласно правилам уже без его участия. • Эти простые правила приводят к огромному разнообразию форм, которые могут возникнуть в игре

John Horton Conway; род. 26 декабря 1937, Ливерпуль) — английский математик, создатель клеточного автомата Игра «Жизнь» .

Нейроавтоматы Нейроматематика

Минский, Марвин Ли • (англ. Marvin Lee Minsky, род. 9 августа 1927) — американский учёный в области искусственного интеллекта

Marvin Minsky • Написал книгу «Персептроны» (с Сеймуром Папертом), ставшая фундаментальной работой для последующих разработок в области искусственных нейронных сетей.

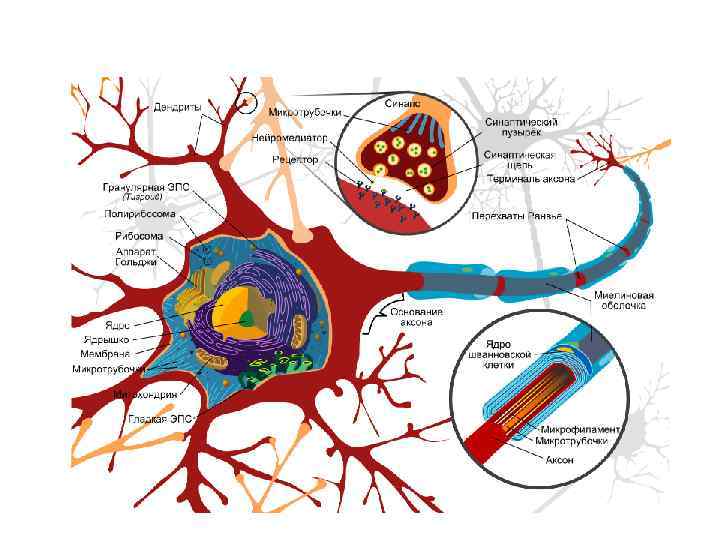
• Нейрон (от др. -греч. — волокно, нерв) — это структурно-функциональная единица нервной системы. • Эта клетка имеет сложное строение, высоко специализирована и по структуре содержит ядро, тело клетки и отростки.

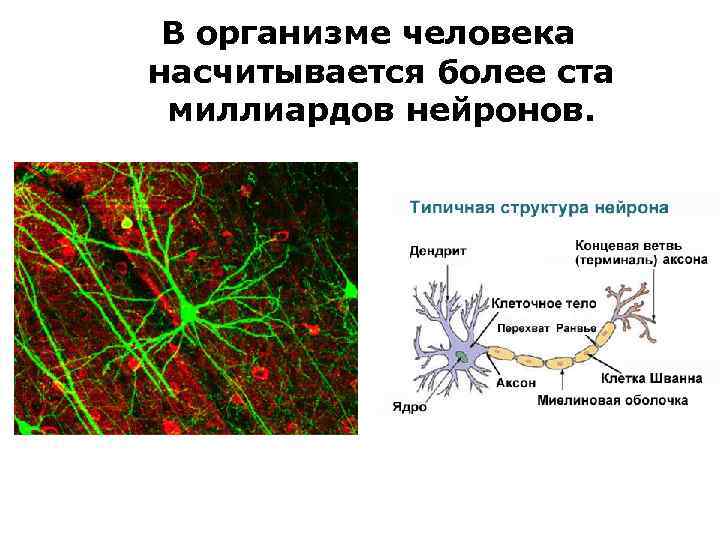В организме человека насчитывается более ста миллиардов нейронов.

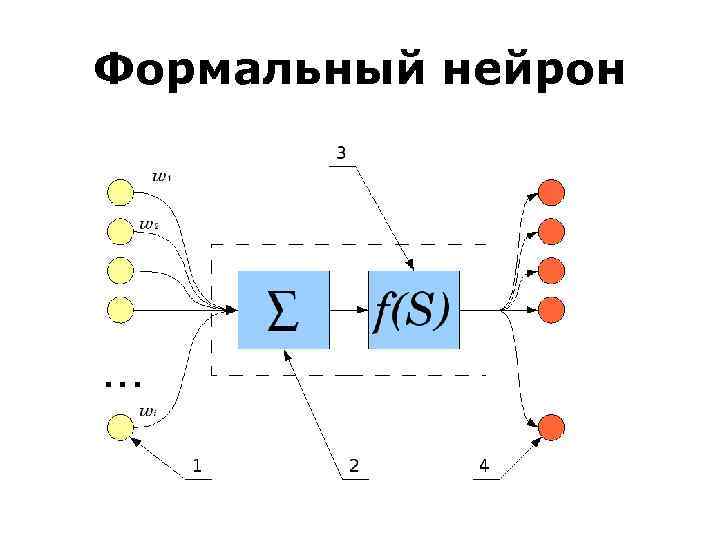Формальный нейрон

• 1. Нейроны, выходные сигналы которых поступают на вход данному 2. Сумматор входных сигналов 3. Вычислитель передаточной функции 4. Нейроны, на входы которых подаётся выходной сигнал данного 5. wi — веса входных сигналов

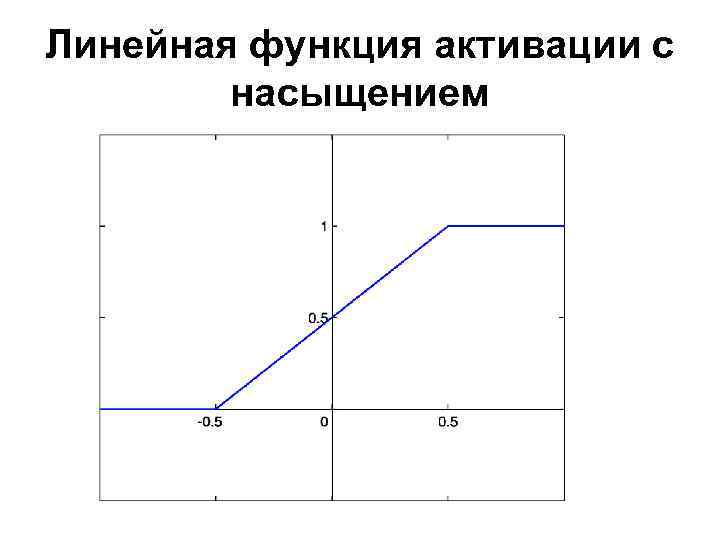Линейная функция активации с насыщением

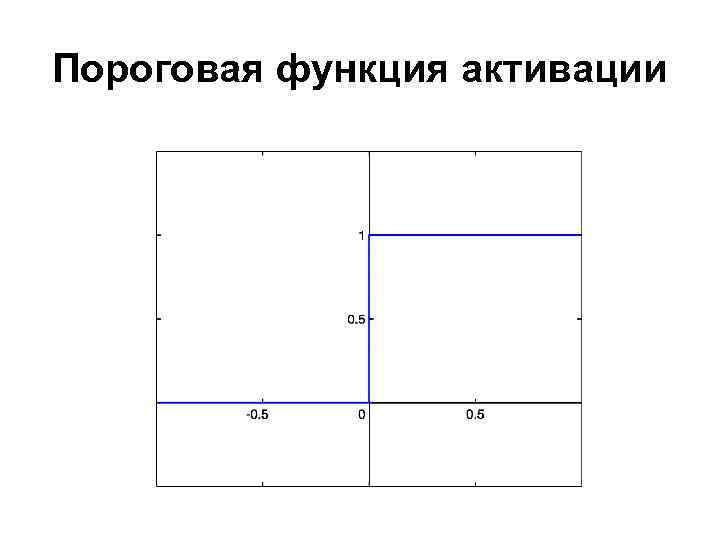Пороговая функция активации

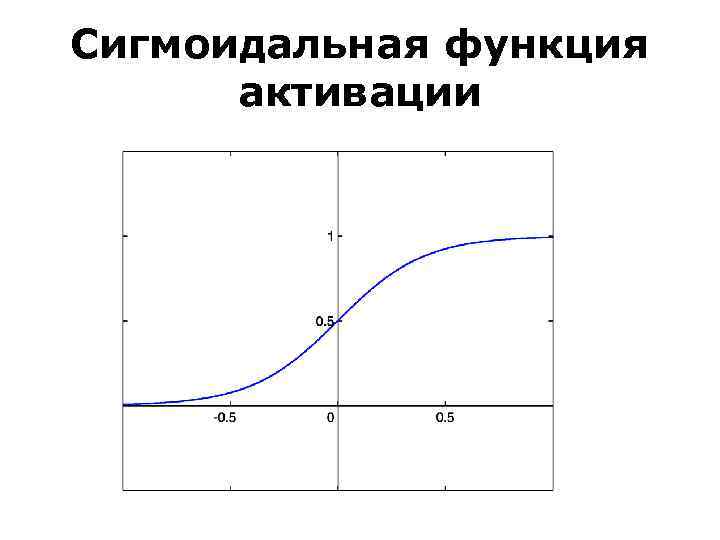Сигмоидальная функция активации

Нейрокомпьютер • Нейрокомпьютер - вычислительная система, в которой • - упрощен до уровня нейрона процессорный элемент однородной структуры; • - резко усложнены связи между элементами; • - программирование заключается в изменении весовых связей между элементами. • Нейроматематика решает математические задачи в нейросетевом логическом базисе.

Нейронная сеть • Нейронная сеть - это сеть с конечным числом слоев из однотипных элементов - аналогов нейронов с различными типами связей между слоями нейронов. • При этом количество нейронов в слоях выбирается необходимым для обеспечения заданного качества решения задачи, а число слоев нейронов - как можно меньшим для уменьшения времени решения задачи. • По существу, нейронная сеть - тоже однородная среда с высокой степенью регулярности

Примеры использования нейросетей • - контроль кредитных карточек (диагностика принадлежности хозяину карточки с настройкой нейронной сети в пространстве признаков покупаемых товаров; • - скрытое обнаружение веществ с помощью устройств на базе тепловых нейронов и нейрокомпьютера на заказных цифровых нейрочипах;

Примеры использования нейросетей • подобная система эксплуатируется во многих аэропортах США при досмотре багажа для выявления наркотиков, взрывчатых веществ, ядерных материалов и т. д. ; • - обработка изображений, например, выделение на изображении движущихся целей, поиск и распознавание объектов заданной формы

Пороговая логика • В 1943 г. Уоррен Мак –Каллок и Уолтер Питтс предложили модель формального нейрона как переключательной функции • Каждый вход (синапс) хi учитывается с некоторым весом w i

• Нейрон возбуждается в случае • ∑w i хi≥ Т & • (00): ∑ =w 1 х1+ w 2 х2=0

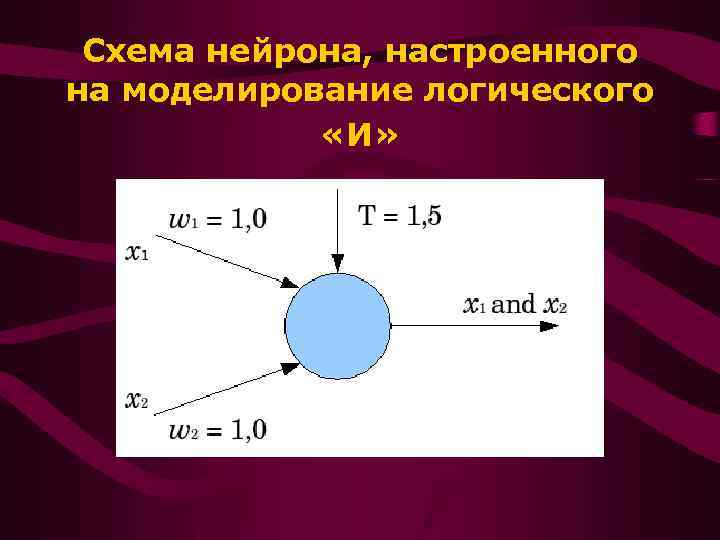Схема нейрона, настроенного на моделирование логического «И»

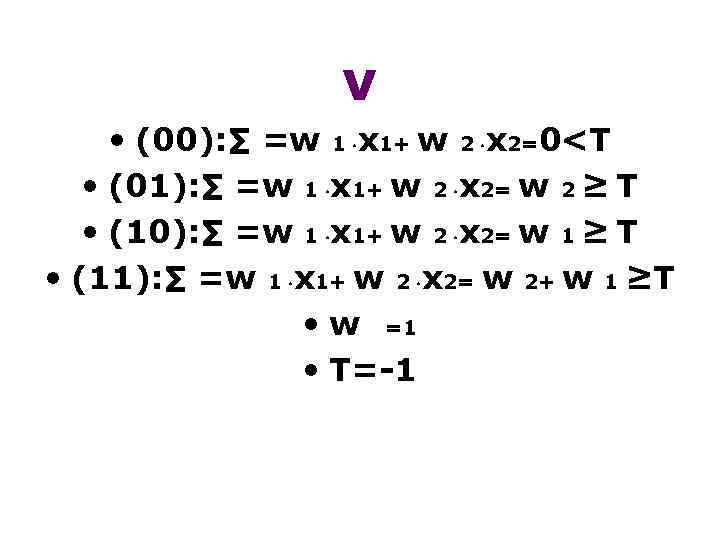ν • (00): ∑ =w 1 х1+ w 2 х2=0

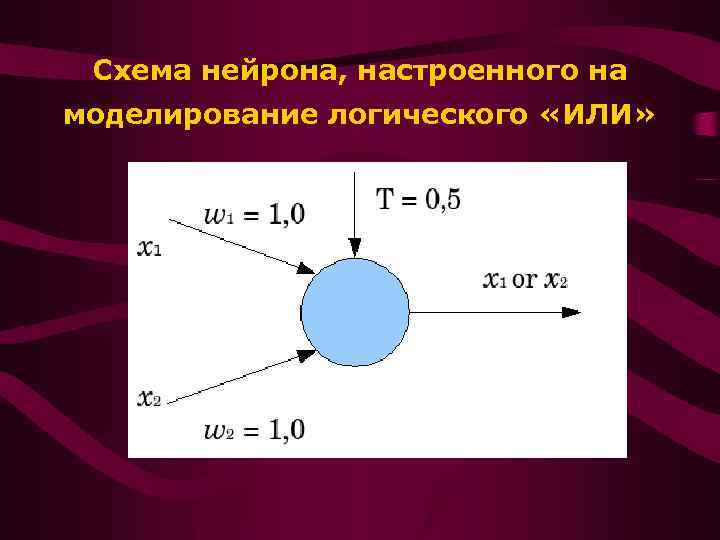Схема нейрона, настроенного на моделирование логического «ИЛИ»

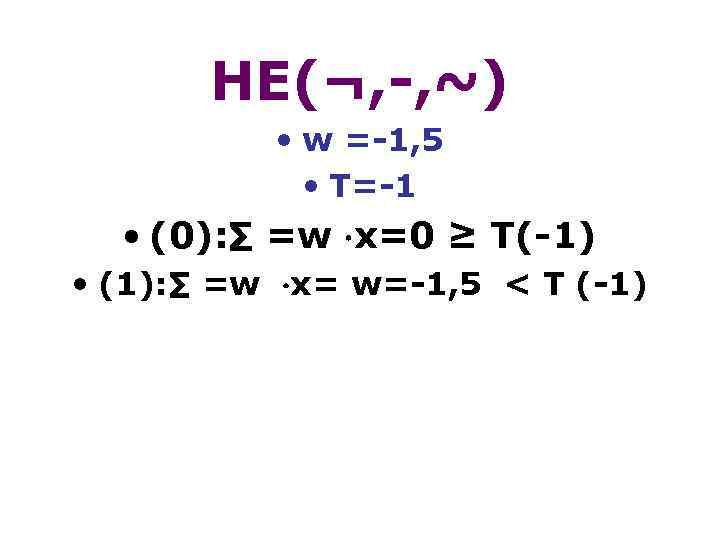НЕ(¬, -, ~) • w =-1, 5 • T=-1 • (0): ∑ =w х=0 ≥ T(-1) • (1): ∑ =w х= w=-1, 5 < T (-1)

Схема нейрона, настроенного на моделирование логического «НЕ»

• Системный анализ

Метод анализа иерархий • Томас Саати (Thomas Saaty). • Electronic Mail: saaty@vms. cis. pitt. edu

• Метод анализа иерархий — МАИ (the analytic hierarchy process — AHP)

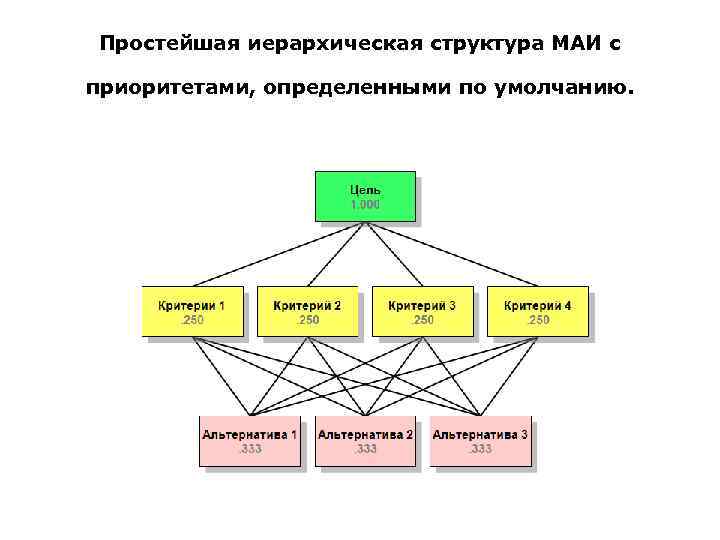Простейшая иерархическая структура МАИ с приоритетами, определенными по умолчанию.

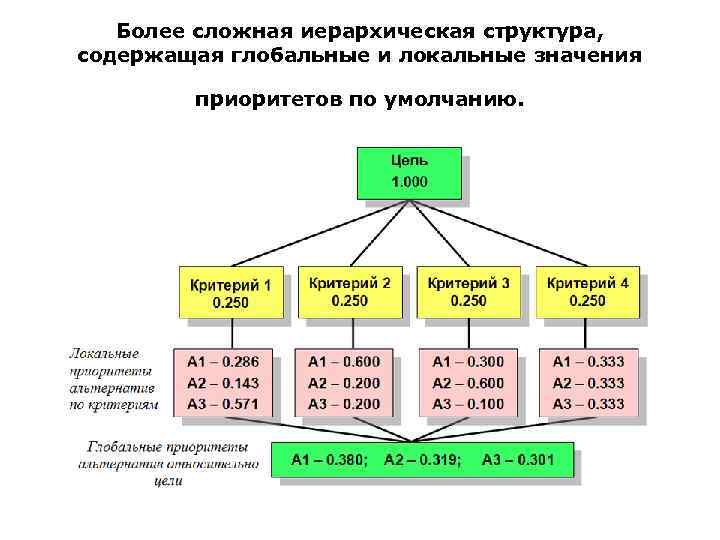Более сложная иерархическая структура, содержащая глобальные и локальные значения приоритетов по умолчанию.

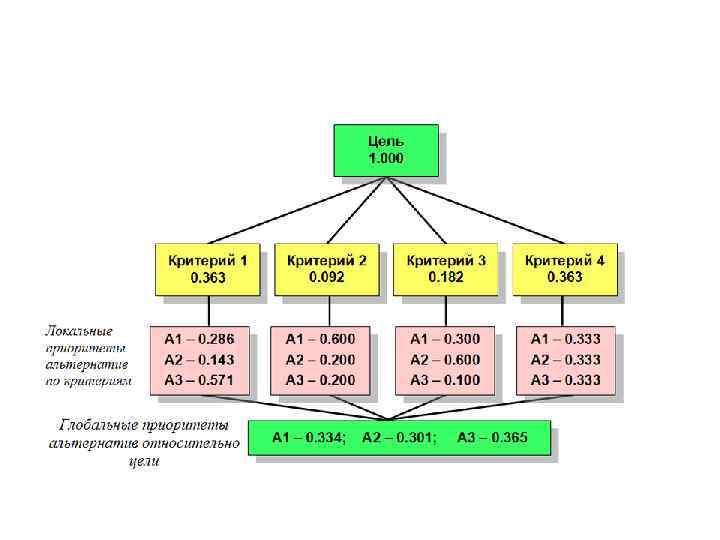
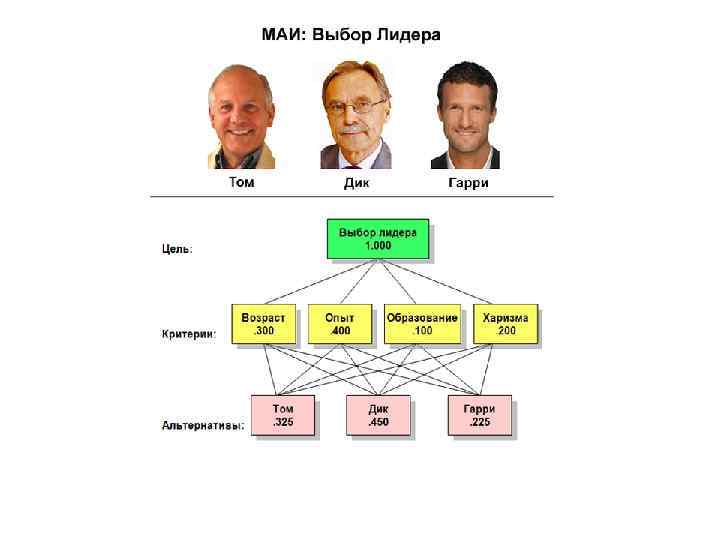
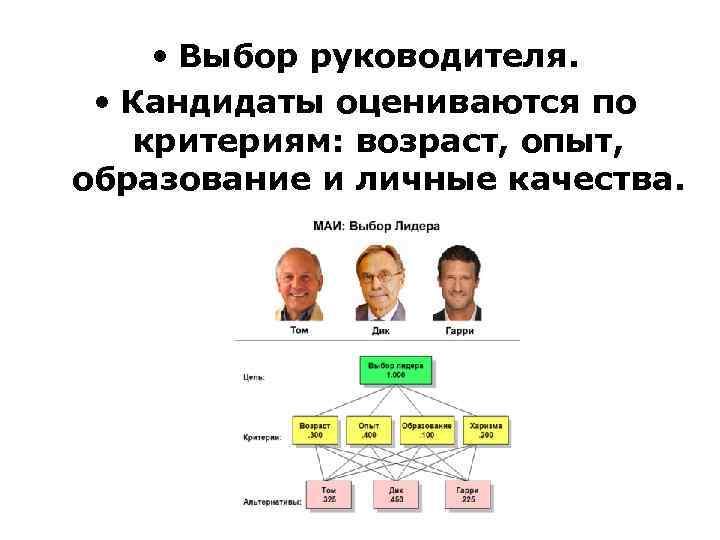• Выбор руководителя. • Кандидаты оцениваются по критериям: возраст, опыт, образование и личные качества.

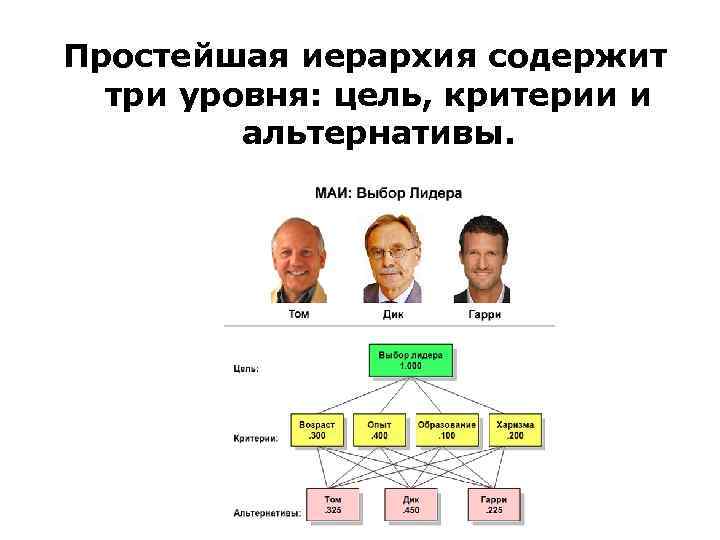Простейшая иерархия содержит три уровня: цель, критерии и альтернативы.

• Числа на рисунке показывают приоритеты элементов иерархии с точки зрения цели, которые вычисляются в МАИ на основе парных сравнений элементов каждого уровня относительно связанных с ними элементами вышерасположенного уровня.

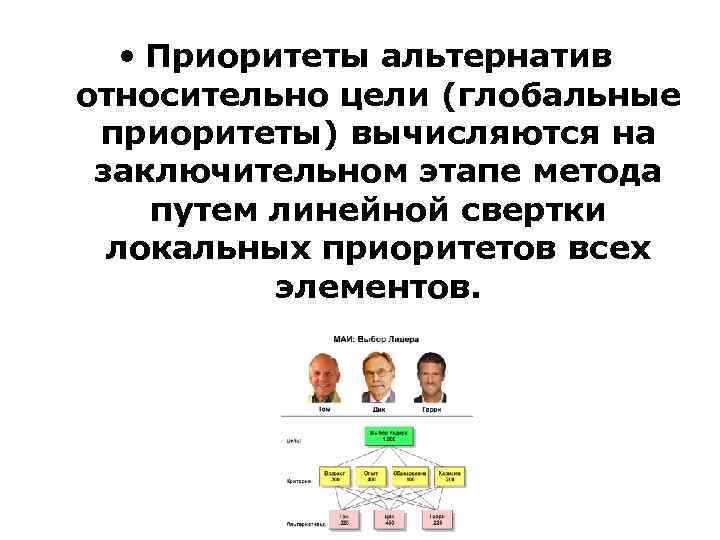• Приоритеты альтернатив относительно цели (глобальные приоритеты) вычисляются на заключительном этапе метода путем линейной свертки локальных приоритетов всех элементов.

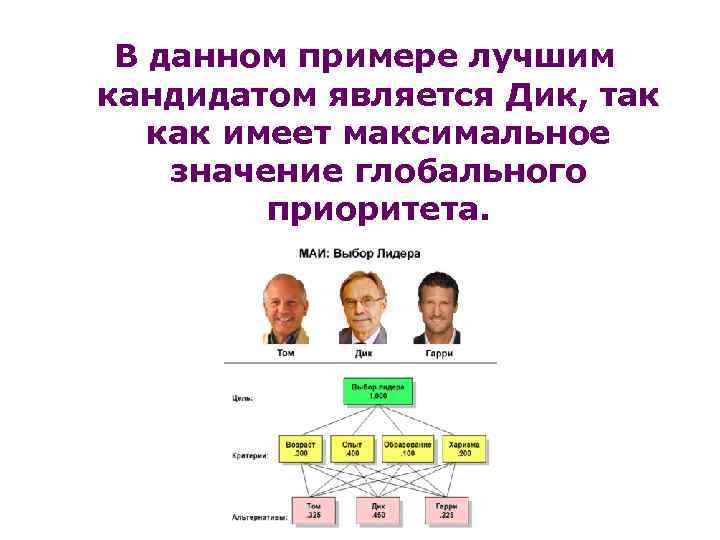В данном примере лучшим кандидатом является Дик, так как имеет максимальное значение глобального приоритета.

Основы теории игр • Теория игр это математическая теория конфликтов. • Конфликт – ситуация, в которой сталкиваются интересы сторон, происходит борьба интересов. Война – конфликт. Говорят «военный конфликт» .