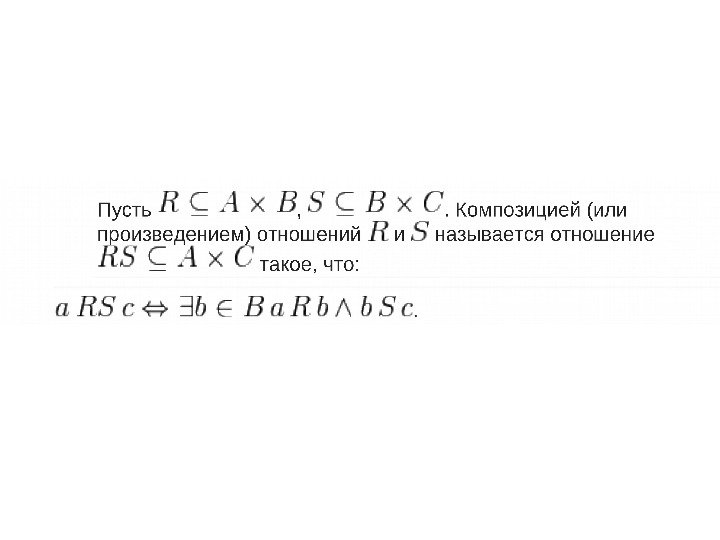• Д. э. н. Л. В. Кальянов















































































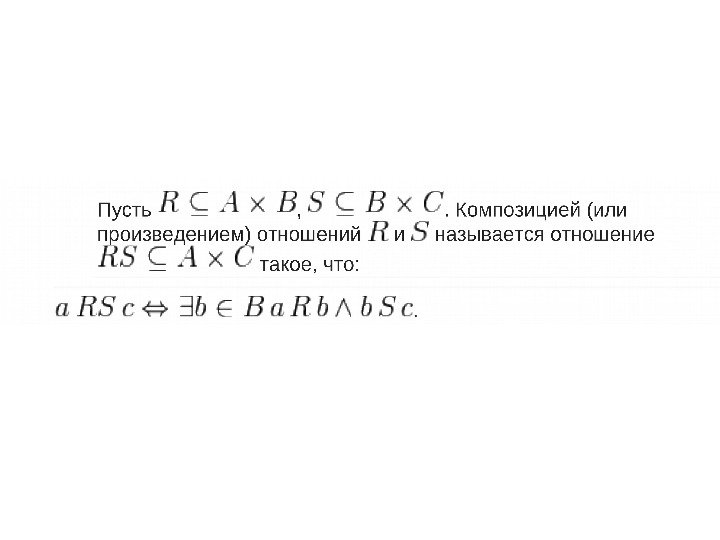


















teriya_mnoghestv.pptx
- Размер: 6.5 Мб
- Автор:
- Количество слайдов: 109
Описание презентации • Д. э. н. Л. В. Кальянов по слайдам
 • Д. э. н. Л. В. Кальянов
• Д. э. н. Л. В. Кальянов


 • В данном курсе можно выделить три главные линии. • Во-первых, в курсе изучаются так называемые основания математики (теория множеств и математическая логика). • Во-вторых– теоретические основы современной информатики(теория алгоритмов и вычислимых функций, теория кодирования, алгебра логики). • В третьих– те факты, методы и конструкции дискретной математики, которые применяются в экономико-математических моделях.
• В данном курсе можно выделить три главные линии. • Во-первых, в курсе изучаются так называемые основания математики (теория множеств и математическая логика). • Во-вторых– теоретические основы современной информатики(теория алгоритмов и вычислимых функций, теория кодирования, алгебра логики). • В третьих– те факты, методы и конструкции дискретной математики, которые применяются в экономико-математических моделях.




 • Часто для обозначения булеана множества M используется выражение. • А для мощности булеана выражение •
• Часто для обозначения булеана множества M используется выражение. • А для мощности булеана выражение •


 • В общем случае, множество A по схеме свертывания определяется как множество, которое содержит все элементы из K, обладающие свойством F. • A = {x| x обладает свойством F}.
• В общем случае, множество A по схеме свертывания определяется как множество, которое содержит все элементы из K, обладающие свойством F. • A = {x| x обладает свойством F}.
 • Применяя сокращение F(x) для обозначения того, что элемент x обладает свойством F, будем писать • A= {x| F(x)}. • Очевидно, что F(x) {0, 1}. • F(x) называется предикатом. • Предик таа (лат. praedicatum — заявленное, упомянутое, сказанное) — это то, что утверждается о субъекте. Субъектом высказывания называется то, о чём делается утверждение.
• Применяя сокращение F(x) для обозначения того, что элемент x обладает свойством F, будем писать • A= {x| F(x)}. • Очевидно, что F(x) {0, 1}. • F(x) называется предикатом. • Предик таа (лат. praedicatum — заявленное, упомянутое, сказанное) — это то, что утверждается о субъекте. Субъектом высказывания называется то, о чём делается утверждение.
 • Неограниченное применение схемы свертывания ведет к противоречиям. Например, можно получить «множество всех множеств» : • M= {x| x– множество}. • Если считать M множеством, то получаем M M. ∈ • Рассмотрим парадокс Рассела, открытый в 1902 году.
• Неограниченное применение схемы свертывания ведет к противоречиям. Например, можно получить «множество всех множеств» : • M= {x| x– множество}. • Если считать M множеством, то получаем M M. ∈ • Рассмотрим парадокс Рассела, открытый в 1902 году.
 • Назовем множество правильным, если оно не является своим элементом, и неправильным в противном случае. Определим множество R как множество всех правильных множеств. Более формально: • R= {x| x R}. ∉
• Назовем множество правильным, если оно не является своим элементом, и неправильным в противном случае. Определим множество R как множество всех правильных множеств. Более формально: • R= {x| x R}. ∉
 • В соответствии с определением для любого множества A справедливо утверждение: • A R тогда и только тогда, когда A A. ∈ ∉ • В частности, если считать R множеством, то его само можно взять в качестве A, но тогда мы придем к противоречию: • R R тогда и только тогда, когда R R. ∈ ∉
• В соответствии с определением для любого множества A справедливо утверждение: • A R тогда и только тогда, когда A A. ∈ ∉ • В частности, если считать R множеством, то его само можно взять в качестве A, но тогда мы придем к противоречию: • R R тогда и только тогда, когда R R. ∈ ∉
 • Более подробно. Если R правильное, то есть не является своим элементом, то оно должно находиться в R, то есть быть своим элементом. • Если же R неправильное, то оно является своим элементом, то есть содержится в R, но R содержит только правильные множества. • Таким образом, R не может быть ни правильным, ни неправильным.
• Более подробно. Если R правильное, то есть не является своим элементом, то оно должно находиться в R, то есть быть своим элементом. • Если же R неправильное, то оно является своим элементом, то есть содержится в R, но R содержит только правильные множества. • Таким образом, R не может быть ни правильным, ни неправильным.




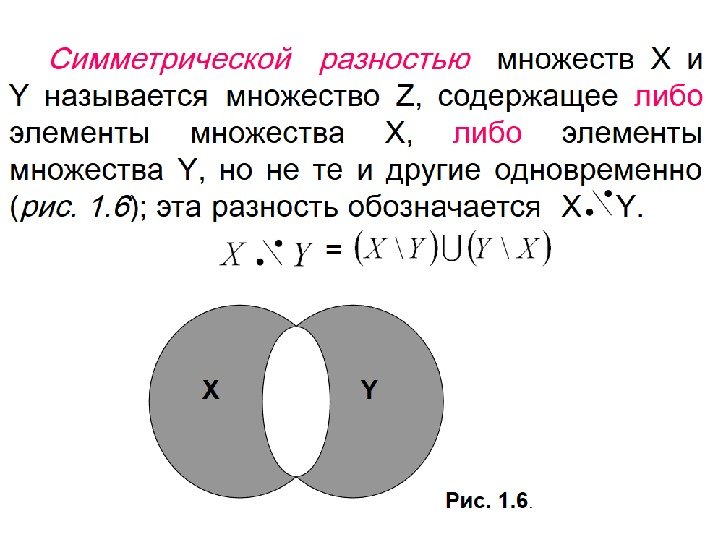
 • Часто для обозначения симметрической разности используется обозначение • •
• Часто для обозначения симметрической разности используется обозначение • •























 • Для обозначения бинарного отношения R на множестве M, будем использовать как обозначение • (a, b) R, • так и обозначение • a. Rb, • где a M, b M
• Для обозначения бинарного отношения R на множестве M, будем использовать как обозначение • (a, b) R, • так и обозначение • a. Rb, • где a M, b M







 Пусть — отнош ение эквивалентност и на м ножестве и . Множествовсехэлем ентов , эквивалентных , т. е. м ножество , называют классом эквивалентностипоотнош ению иобозначают . Отм етим , чтовсилурефлексивностидлялюбого элем ента класс эквивалентностинепуст, так как .
Пусть — отнош ение эквивалентност и на м ножестве и . Множествовсехэлем ентов , эквивалентных , т. е. м ножество , называют классом эквивалентностипоотнош ению иобозначают . Отм етим , чтовсилурефлексивностидлялюбого элем ента класс эквивалентностинепуст, так как .
 Т е о р е м а 1. 1. Дл ял ю б о г оо т н о ш е н и я экви ва л е н т н о с т и н ам н о же с т в е м но же с т вокл а с с о в экви ва л е н т н о с т и о б р а зу е тр а зб и е н и ем н о же с т в а . О б р а т н о , л юб о ер а зб и е ни ем н о же с т ва за да е тн а н е м о т н о ш е н и еэкви ва л е н т н о с т и, дл яко т о р о г о кл а с с ы экви ва л е н т н о с т и с о вп а да ю тсэл е м е н т а м и р а зб и е н и я.
Т е о р е м а 1. 1. Дл ял ю б о г оо т н о ш е н и я экви ва л е н т н о с т и н ам н о же с т в е м но же с т вокл а с с о в экви ва л е н т н о с т и о б р а зу е тр а зб и е н и ем н о же с т в а . О б р а т н о , л юб о ер а зб и е ни ем н о же с т ва за да е тн а н е м о т н о ш е н и еэкви ва л е н т н о с т и, дл яко т о р о г о кл а с с ы экви ва л е н т н о с т и с о вп а да ю тсэл е м е н т а м и р а зб и е н и я.
 Покажем, что отношениеэквивал ентности на м ножестве определяет некотороеразбиениеэтого м ножества. Убедим сявначале, чтолюбыедвакласса эквивалентности поотнош ению либонепересекаются, либо совпадают.
Покажем, что отношениеэквивал ентности на м ножестве определяет некотороеразбиениеэтого м ножества. Убедим сявначале, чтолюбыедвакласса эквивалентности поотнош ению либонепересекаются, либо совпадают.
 Пустьдваклассаэквивалентностииим еютобщ ий элем ент. Тогдаи. Всилу сим м етричностиотнош енияим еем, и тогдаи. Всилутранзитивности отнош енияполучим. Пусть, тогда. Так как, тои, следовательно, .
Пустьдваклассаэквивалентностииим еютобщ ий элем ент. Тогдаи. Всилу сим м етричностиотнош енияим еем, и тогдаи. Всилутранзитивности отнош енияполучим. Пусть, тогда. Так как, тои, следовательно, .
 Обратно, если , товсилу сим м етричности получим и всилу транзитивности — , тоесть . Таким образом , .
Обратно, если , товсилу сим м етричности получим и всилу транзитивности — , тоесть . Таким образом , .












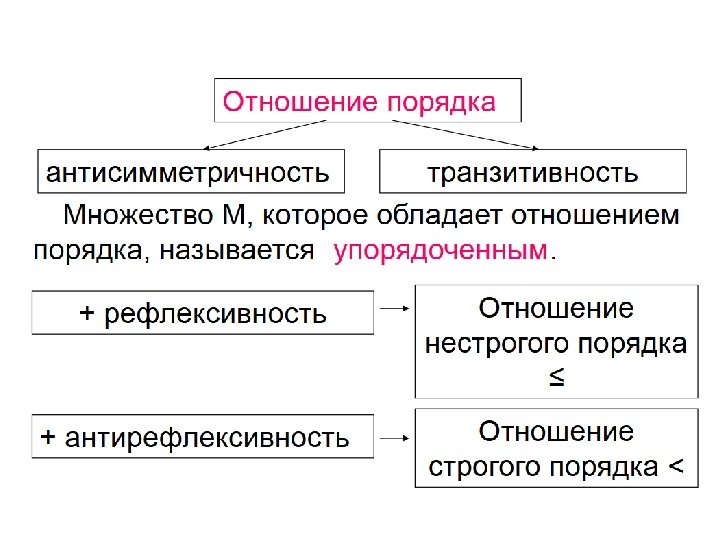
 Отношение порядка. • Пусть А– непустое множество. • Определение. Отношение Р А ⊆ называется предпорядком (квази-порядком), если оно рефлексивно и транзитивно.
Отношение порядка. • Пусть А– непустое множество. • Определение. Отношение Р А ⊆ называется предпорядком (квази-порядком), если оно рефлексивно и транзитивно.
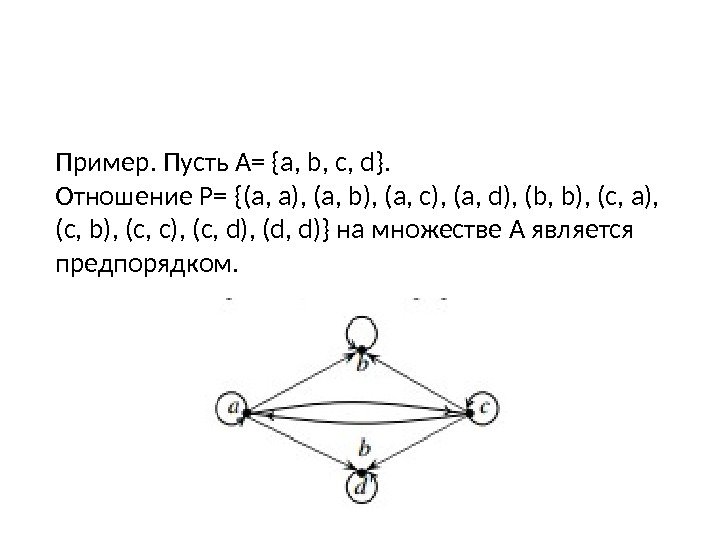
 Пример. Пусть А= {a, b, c, d}. Отношение Р= {(a, a), (a, b), (a, c), (a, d), (b, b), (c, a), (c, b), (c, c), (c, d), (d, d)} на множестве А является предпорядком.
Пример. Пусть А= {a, b, c, d}. Отношение Р= {(a, a), (a, b), (a, c), (a, d), (b, b), (c, a), (c, b), (c, c), (c, d), (d, d)} на множестве А является предпорядком.
 • Определение. Отношение Р А ⊆ называется частичным порядком, если оно рефлексивно, транзитивно и антисимметрично. Таким образом, частичный порядок представляет собой антисимметричный предпорядок. Частичный порядок обозначается символом ≤.
• Определение. Отношение Р А ⊆ называется частичным порядком, если оно рефлексивно, транзитивно и антисимметрично. Таким образом, частичный порядок представляет собой антисимметричный предпорядок. Частичный порядок обозначается символом ≤.
 • Определение. Отношение < А ⊆ называется строгим порядком, если оно определяется по следующему правилу: ( ∀ x, y A) х < у х ≤ у и х ≠ у. ∈ ⇔ • Отношение строгого порядка не является частичным порядком, так как оно не рефлексивно.
• Определение. Отношение < А ⊆ называется строгим порядком, если оно определяется по следующему правилу: ( ∀ x, y A) х < у х ≤ у и х ≠ у. ∈ ⇔ • Отношение строгого порядка не является частичным порядком, так как оно не рефлексивно.
 • Определение. Пусть ≤ А и х, у А. ⊆ ∈ Элементы х и у называются несравнимыми, если нельзя сказать, что х ≤ у или у ≤ х. • Пример. Пусть А= {a, b, c, d}. Отношение включения на булеане P(A) является ⊆ частичным порядком. Элементы B= {a, c} и C= {b, d} из P(A) • являются несравнимыми, так как(B, C) ∉ ⊆ и(C, B) . ∉ ⊆
• Определение. Пусть ≤ А и х, у А. ⊆ ∈ Элементы х и у называются несравнимыми, если нельзя сказать, что х ≤ у или у ≤ х. • Пример. Пусть А= {a, b, c, d}. Отношение включения на булеане P(A) является ⊆ частичным порядком. Элементы B= {a, c} и C= {b, d} из P(A) • являются несравнимыми, так как(B, C) ∉ ⊆ и(C, B) . ∉ ⊆
 • Определение. Частичный порядок ≤ А ⊆ называется линейным порядком, если( х, ∀ у А) х ≤ у или у ≤ х. ∈ • Определение. Пусть А ≠ и ≤– ∅ частичный(линейный) порядок на А. • Упорядоченная пара называется частично(линейно) упорядоченным множеством.
• Определение. Частичный порядок ≤ А ⊆ называется линейным порядком, если( х, ∀ у А) х ≤ у или у ≤ х. ∈ • Определение. Пусть А ≠ и ≤– ∅ частичный(линейный) порядок на А. • Упорядоченная пара называется частично(линейно) упорядоченным множеством.
 • Пример. Пара , где ≤– отношение делимости на множестве Z, является частичным, но не линейным порядком. • Пары , с обычными отношениями ≤ образуют линейно упорядоченные множества.
• Пример. Пара , где ≤– отношение делимости на множестве Z, является частичным, но не линейным порядком. • Пары , с обычными отношениями ≤ образуют линейно упорядоченные множества.
 • Определение. Элемент а А частично ∈ упорядоченного множества называется максимальным(минимальным), если( х А) а ≤ х(х ≤ а) х = а. ∀ ∈ ⇒ • Определение. Элемент а А частично ∈ упорядоченного множества называется наибольшим(наименьшим), если( х А) х ≤ а(а ≤ х). ∀ ∈
• Определение. Элемент а А частично ∈ упорядоченного множества называется максимальным(минимальным), если( х А) а ≤ х(х ≤ а) х = а. ∀ ∈ ⇒ • Определение. Элемент а А частично ∈ упорядоченного множества называется наибольшим(наименьшим), если( х А) х ≤ а(а ≤ х). ∀ ∈
 • Наибольший(наименьший) элемент частично упорядоченного множества • (если он существует) обозначается через max A (min А).
• Наибольший(наименьший) элемент частично упорядоченного множества • (если он существует) обозначается через max A (min А).
 • Теорема. Пусть является частично упорядоченным множеством, где А– непустое и конечное множество. Тогда содержит хотя бы один минимальный элемент, и если он является единственным, то он также является и наименьшим. Аналогично, содержит хотя бы один максимальный элемент, и если он является единственным, то он также является наибольшим.
• Теорема. Пусть является частично упорядоченным множеством, где А– непустое и конечное множество. Тогда содержит хотя бы один минимальный элемент, и если он является единственным, то он также является и наименьшим. Аналогично, содержит хотя бы один максимальный элемент, и если он является единственным, то он также является наибольшим.
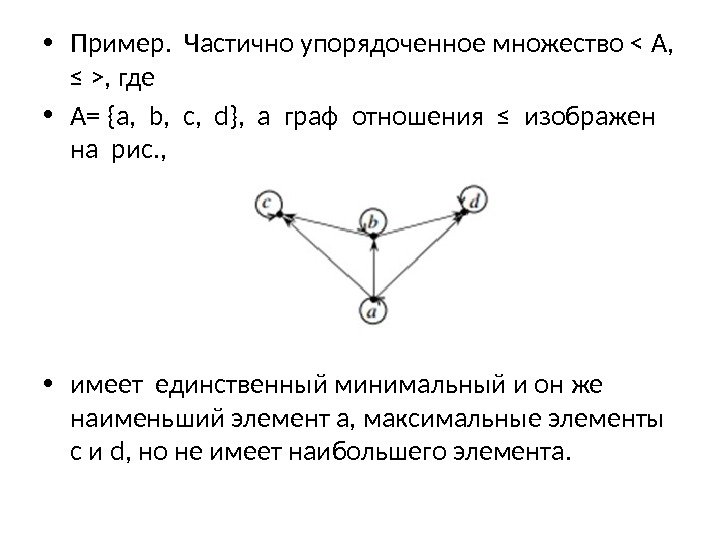
 • Пример. Частично упорядоченное множество , где • А= {a, b, c, d}, а граф отношения ≤ изображен на рис. , • имеет единственный минимальный и он же наименьший элемент a, максимальные элементы c и d, но не имеет наибольшего элемента.
• Пример. Частично упорядоченное множество , где • А= {a, b, c, d}, а граф отношения ≤ изображен на рис. , • имеет единственный минимальный и он же наименьший элемент a, максимальные элементы c и d, но не имеет наибольшего элемента.
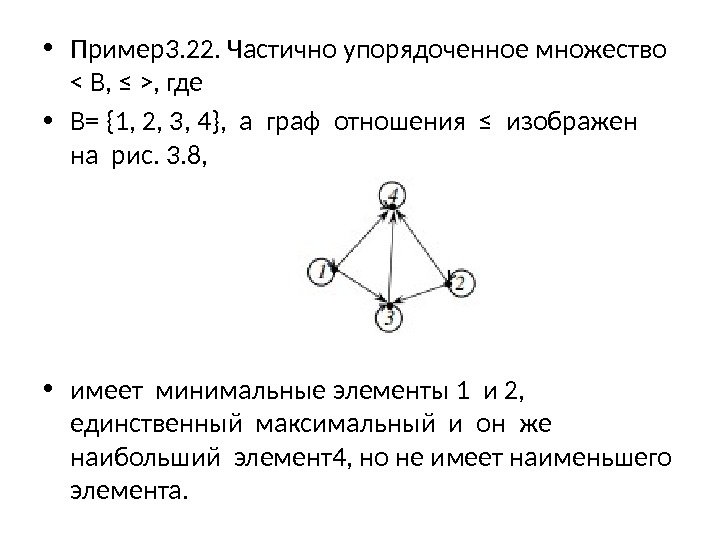
 • Пример3. 22. Частично упорядоченное множество , где • B= {1, 2, 3, 4}, а граф отношения ≤ изображен на рис. 3. 8, • имеет минимальные элементы 1 и 2, единственный максимальный и он же наибольший элемент4, но не имеет наименьшего элемента.
• Пример3. 22. Частично упорядоченное множество , где • B= {1, 2, 3, 4}, а граф отношения ≤ изображен на рис. 3. 8, • имеет минимальные элементы 1 и 2, единственный максимальный и он же наибольший элемент4, но не имеет наименьшего элемента.
 • Замечание. Всякий наибольший элемент частично упорядоченного множества является максимальным, а всякий наименьший элемент – минимальным. Обратное утверждение, вообще говоря, неверно.
• Замечание. Всякий наибольший элемент частично упорядоченного множества является максимальным, а всякий наименьший элемент – минимальным. Обратное утверждение, вообще говоря, неверно.



 Операции над отношениями • Так как отношения, заданные на фиксированной паре множеств являются подмножества A B, то можно определить операции объединения, пересечения и дополнения отношений.
Операции над отношениями • Так как отношения, заданные на фиксированной паре множеств являются подмножества A B, то можно определить операции объединения, пересечения и дополнения отношений.

 • Часто вместо объединения, пересечения и дополнения отношений говорят об их дизъюнкции, конъюнкции и отрицании.
• Часто вместо объединения, пересечения и дополнения отношений говорят об их дизъюнкции, конъюнкции и отрицании.