הטכניון — מכון טכנולוגי לישראל TECHNION

הטכניון - מכון טכנולוגי לישראל TECHNION - ISRAEL INSTITUTE OF TECHNOLOGY הפקולטה להנדסת חשמל המעבדה לבקרה ורובוטיקה בקרת Sliding Mode של מערכת עקיבה סטודנטים : ניר שחם הילה מרדכי מנחה : ולדיסלב זסלבסקי

מבנה המצגת • תיאור הפרויקט ומטרתו. • תיאור המערך המעבדתי. • תיאור שיטת Sliding Mode Control ובניית הבקר. • הצגת סימולציות והרצות על המערך המעבדתי.

מבנה המצגת )המשך( • השוואה לבקר . PD • תיאור שיטת . Global Sliding Mode Control • סיכום ומסקנות.

תיאור הפרויקט ומטרתו תכנון בקר Sliding Mode עבור מערכת של זרוע גמיש המונעת ע"י מנוע . DC בשלב הראשון תכנון עבור המערכת המופשטת הכוללת מנוע DC בלבד. בשלב השני תכנון עבור המערכת המלאה הכוללת מנוע DC וזרוע גמיש. כמו כן תיבדק האפשרות לתכן בקר בשיטת . Global Sliding Mode

תיאור המערך המעבדתי המערכת מורכבת מהחלקים הבאים: 1. מערכת סרוו 20 - : SRV . מנוע DC מוזן על ידי מתח ישר של זווית הרוטור נמדדת בעזרת פוטנציומטר.

תיאור המערך המעבדתי )המשך I ( 2. יחידת ה- : (Rotary Flexible Joint) , RFJ מורכבת מגוף ומעומס. זווית סטיית הזרוע נמדדת בעזרת פוטנציומטר, חיבור גמיש מיוצג על ידי שני קפיצים זהים שנעגנים הן לגוף והן לעומס.

תיאור המערך המעבדתי )המשך II 3. תוכנת ה- ( : Win. Con מיועדת למימוש בקר בעזרת מחשב, להפעלת מערכת בקרה בזמן אמת ולהצגת הביצועים.

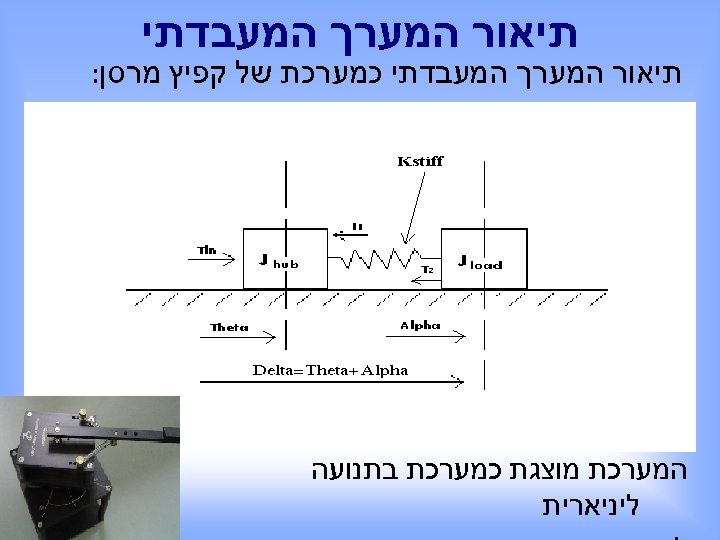
תיאור המערך המעבדתי כמערכת של קפיץ מרסן: המערכת מוצגת כמערכת בתנועה ליניארית

תיאור משוואות הדינמיקה לאחר פיתוח המשוואות המתארות את המערכת נקבל: . )1( . )2( המערכת המובאת כאן היא ללא ריסון למרות שקיים ריסון אך הוא זניח

תיאור משוואות הדינמיקה )המשך ( I עבור המערכת המופשטת )הכוללת רק את ( נקבל:

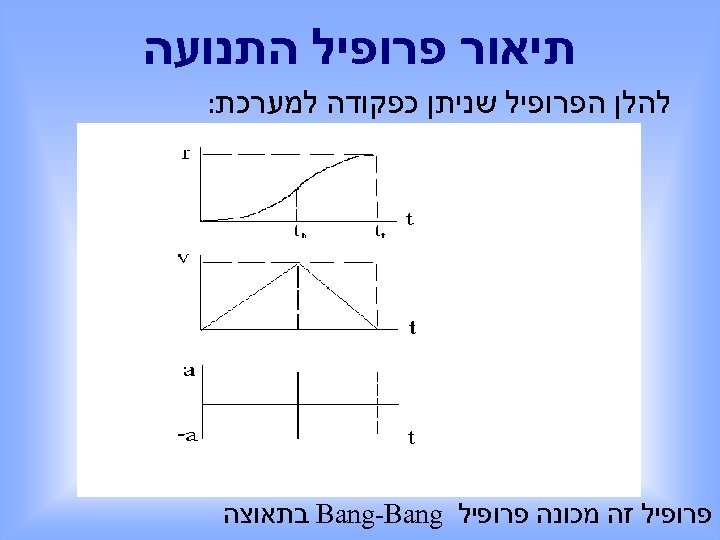
תיאור פרופיל התנועה להלן הפרופיל שניתן כפקודה למערכת: פרופיל זה מכונה פרופיל Bang-Bang בתאוצה

תיאור פרופיל התנועה )המשך I ( ההגדרות עבור המשתנים הן כדלקמן: ערך סופי זוויתי של הפקודה. משתנה המצב הזוויתי. פרופיל תנועה זוויתית רצויה. חצי מזמן ההגעה הסופי. זמן הגעה סופי. הפרופיל שאנו מעוניינים בו נבנה עפ"י הדרישות הבאות:

תיאור שיטת Sliding Mode עקרון מנחה : החלפת המערכת מסדר n מסדר למערכת ראשון ובקרה עליה תכונות כלליות : v בקרה לא ליניארית. v רובסטית לאי-ודאויות בפרמטרים ואי-דיוק במידול המערכת. v רובסטית להפרעות. v משטח החלקה ) – (Sliding Surface פונקציה של משתני המצב. v הבקרה כוללת שני שלבים: א. הבאת המערכת ל- Sliding Surface תוך זמן סופי.

תיאור שיטת ) SMC המשך ( I המטרה: עקיבה של מערכת ליניארית מסדר n אחרי פקודה. כאשר: רכיבי וקטור המצב המדוד. - פרמטרים. הבעיה: השתנות הפרמטרים של המערכת בזמן:

תיאור שיטת ) SMC המשך ( II נגדיר וקטור שגיאה: כאשר : - n סדר המערכת. - וקטור המצב הרצוי )פקודה(. נגדיר פונקציה סקלרית: כאשר 2= n מתקבל:

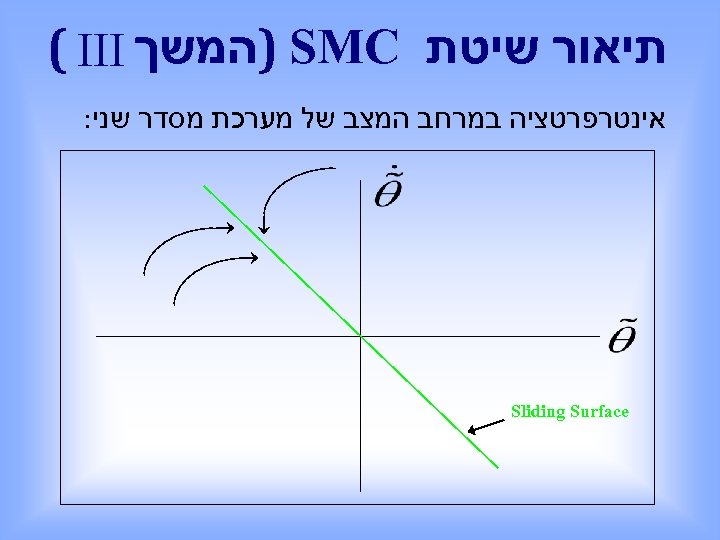
תיאור שיטת ) SMC המשך ( III אינטרפרטציה במרחב המצב של מערכת מסדר שני: Sliding Surface

תיאור שיטת ) SMC המשך ( IV בעיית העקיבה של הוקטור ה- n ממדי ניתנת להחלפה לבעיית יציבות מסדר ראשון ב- , s שהינה : חיובי. , כאשר

תיאור שיטת ) SMC המשך ( V המטרה היא : עבור פונקצית ליאפונוב הבאה: נדרש למצוא u כך ש- מוגדרת. תהיה שלילית

פיתוח Sliding Mode עבור המערכת המופשטת בקר עבור המערכת המופשטת קבלנו: נגדיר אות בקרה ממוצע : חוק הבקרה נתון ע"י : משטח ההחלקה

תוצאות סימולציה והפעלת המערך המעבדתי תיאור התוצאות שיוצגו: v סימולציות עבור המערכת המופשטת + תגובה להפרעה. v סימולציות עבור המערכת המלאה ללא בקרה על + להפרעה. תגובה v סימולציות עבור המערכת המלאה עם בקרה על + להפרעה. תגובה v הפעלת המערך המעבדתי עם הבקר + תגובה להפרעה. v סימולציה עבור בקר + PD תגובה להפרעה. v הפעלת המערך המעבדתי עם בקר + PD תגובה להפרעה.

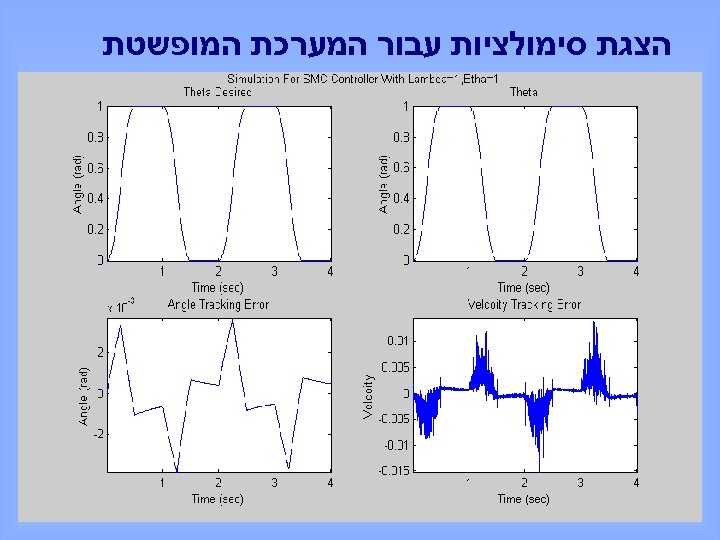
הצגת סימולציות עבור המערכת המופשטת

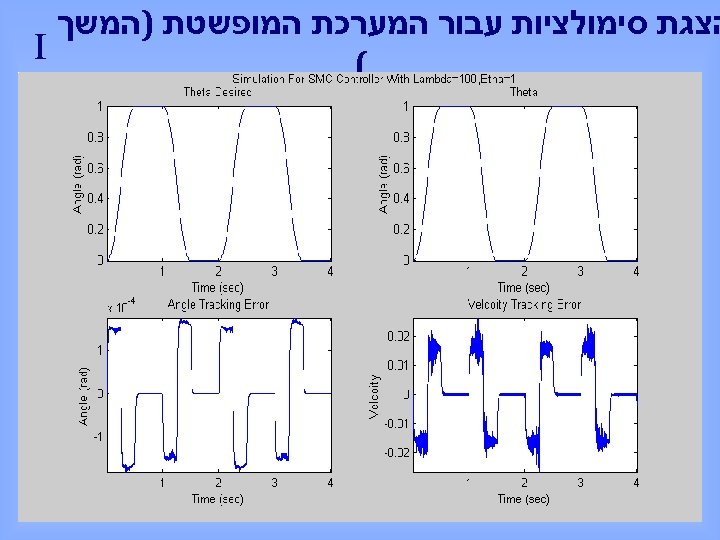
הצגת סימולציות עבור המערכת המופשטת )המשך I (

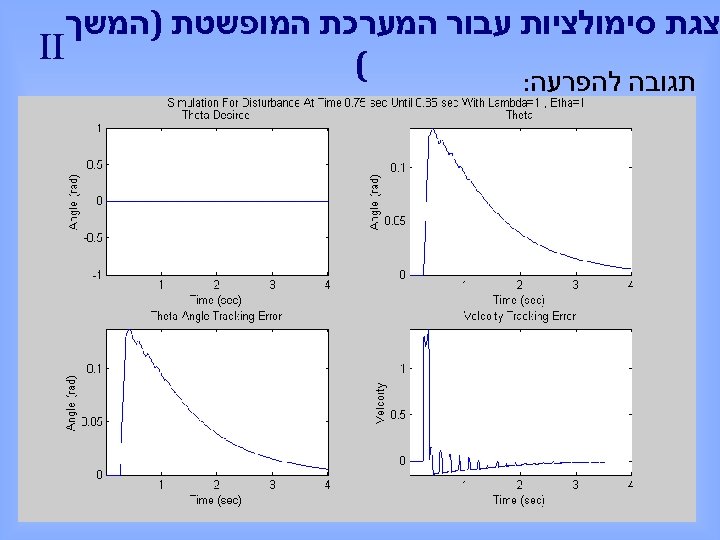
צגת סימולציות עבור המערכת המופשטת )המשך II ( תגובה להפרעה:

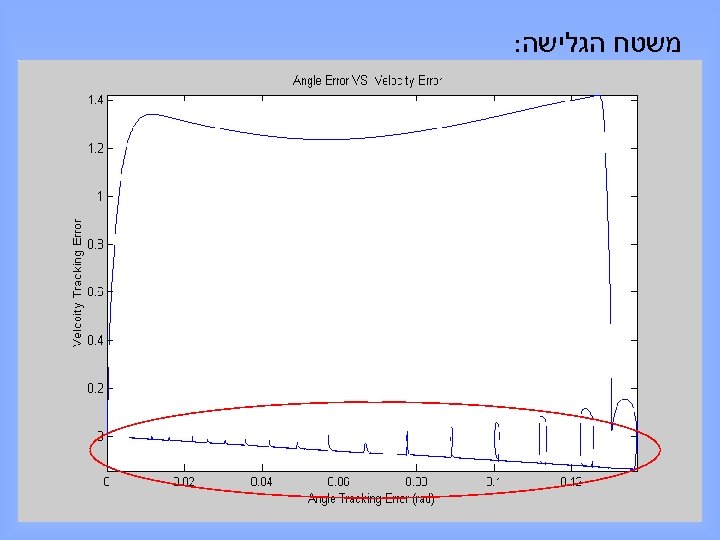
משטח הגלישה:

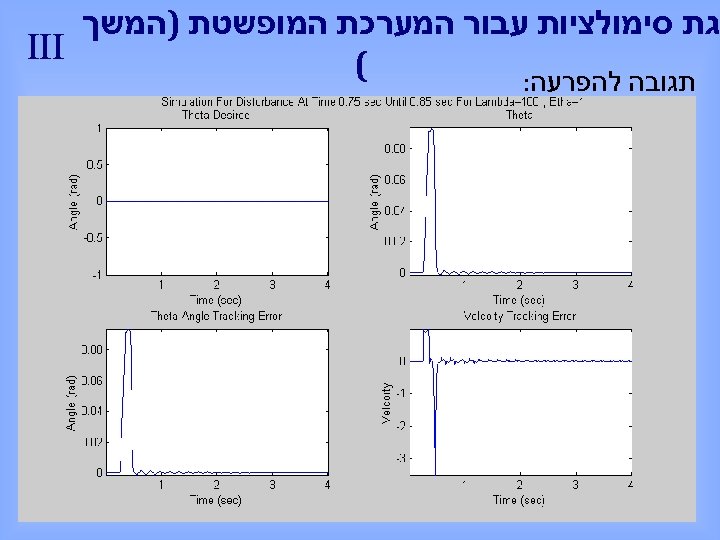
גת סימולציות עבור המערכת המופשטת )המשך III ( תגובה להפרעה:

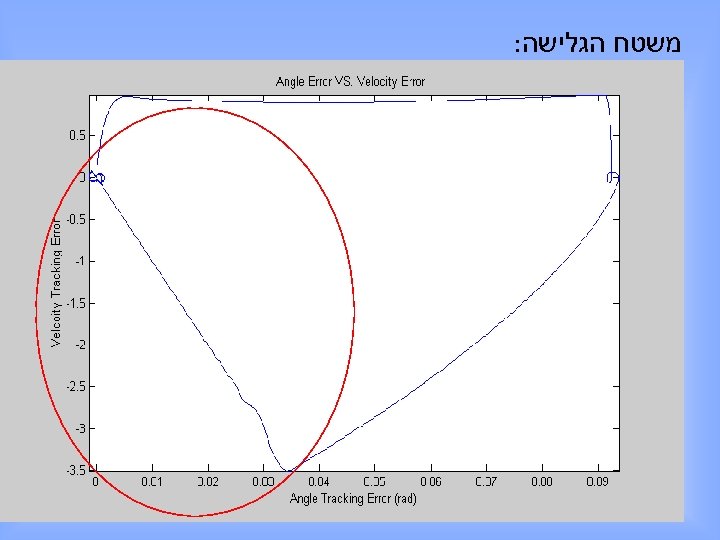
משטח הגלישה:

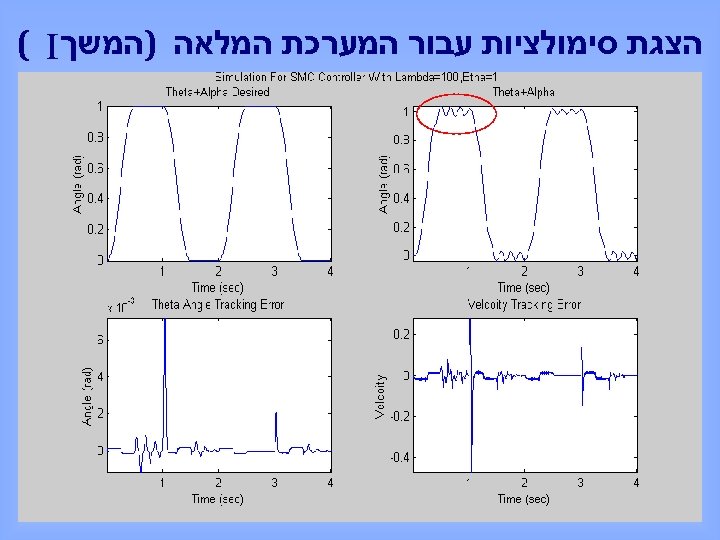
הצגת סימולציות עבור המערכת המלאה )המשך ( I

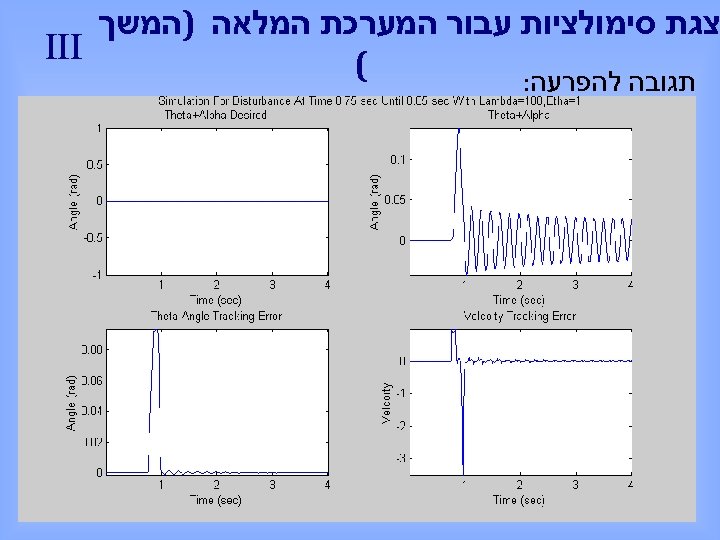
צגת סימולציות עבור המערכת המלאה )המשך III ( תגובה להפרעה:

פיתוח בקר Sliding Mode עבור המערכת המלאה קבלנו: חוק הבקרה נתון ע"י :

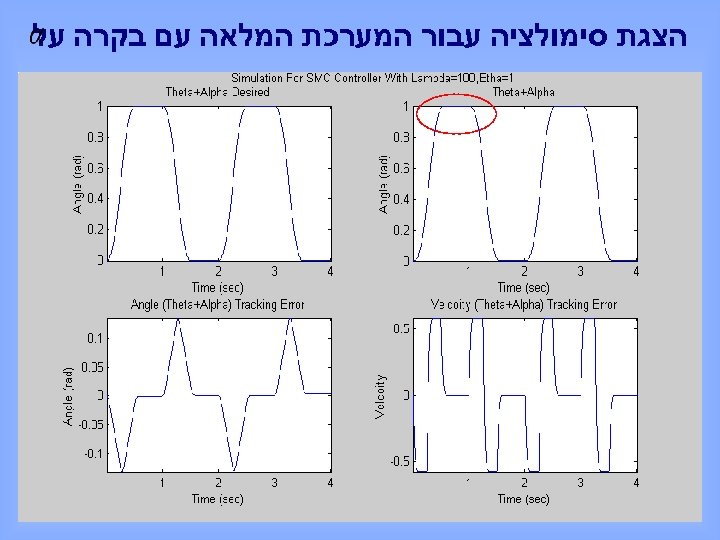
הצגת סימולציה עבור המערכת המלאה עם בקרה על

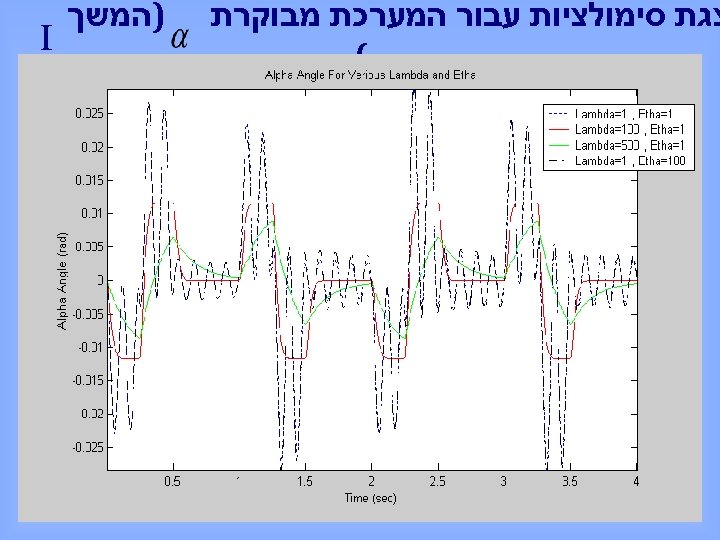
צגת סימולציות עבור המערכת מבוקרת ( )המשך I

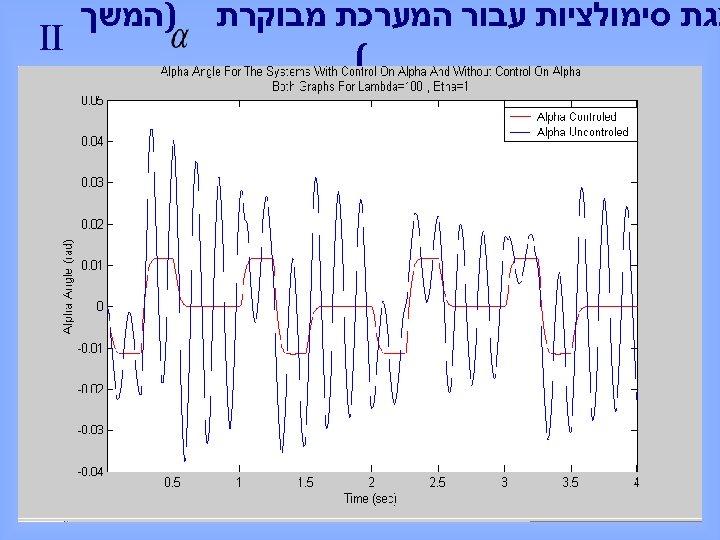
צגת סימולציות עבור המערכת מבוקרת ( )המשך II

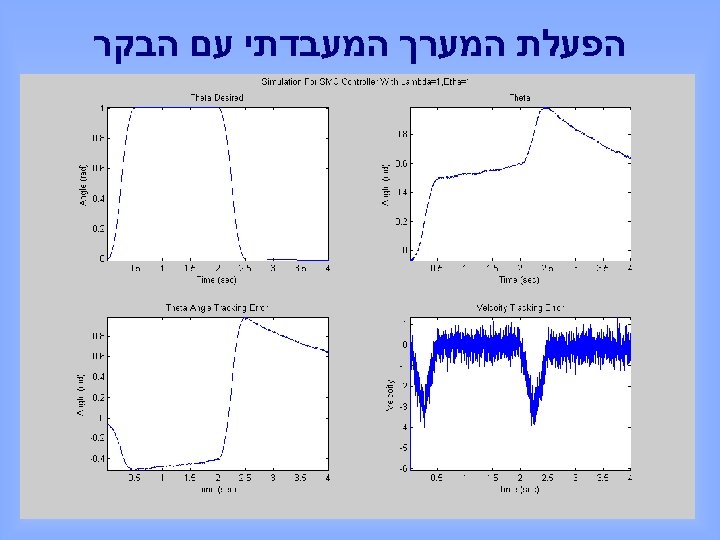
הפעלת המערך המעבדתי עם הבקר

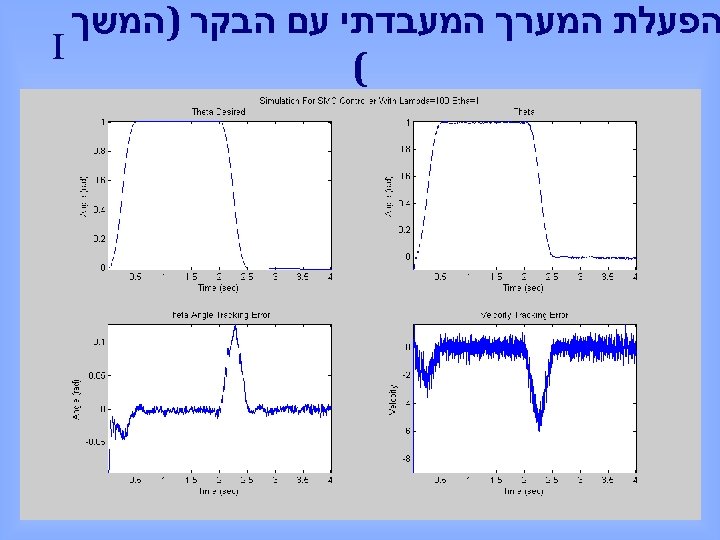
הפעלת המערך המעבדתי עם הבקר )המשך I (

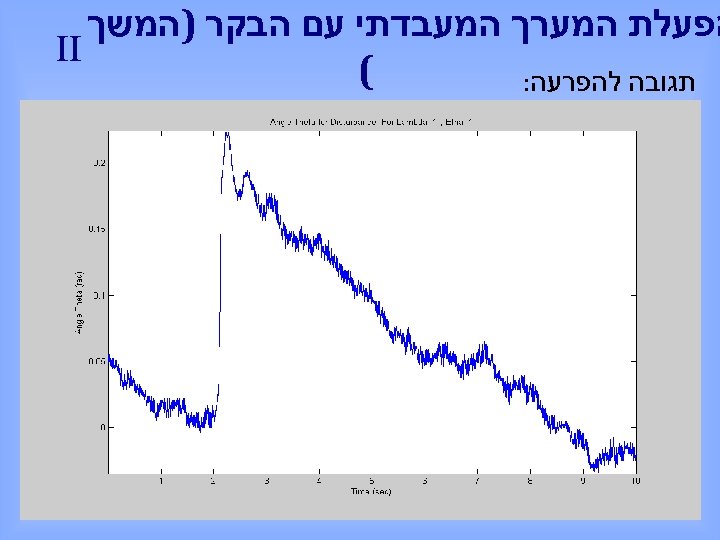
הפעלת המערך המעבדתי עם הבקר )המשך II ( תגובה להפרעה:

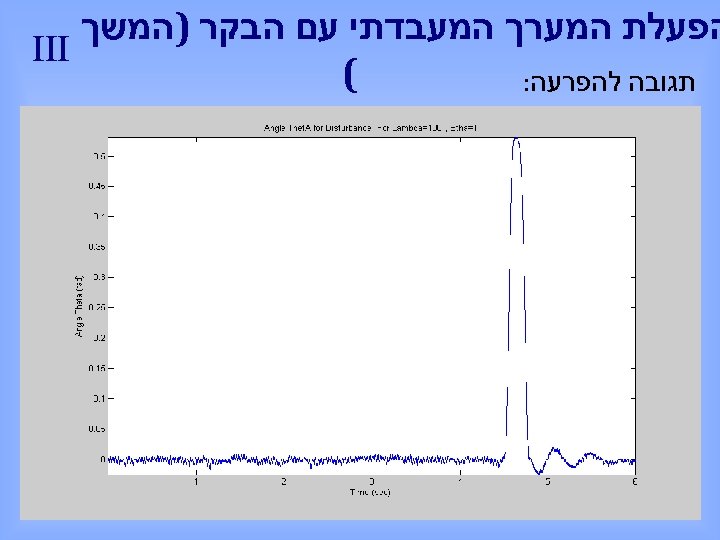
הפעלת המערך המעבדתי עם הבקר )המשך III ( תגובה להפרעה:

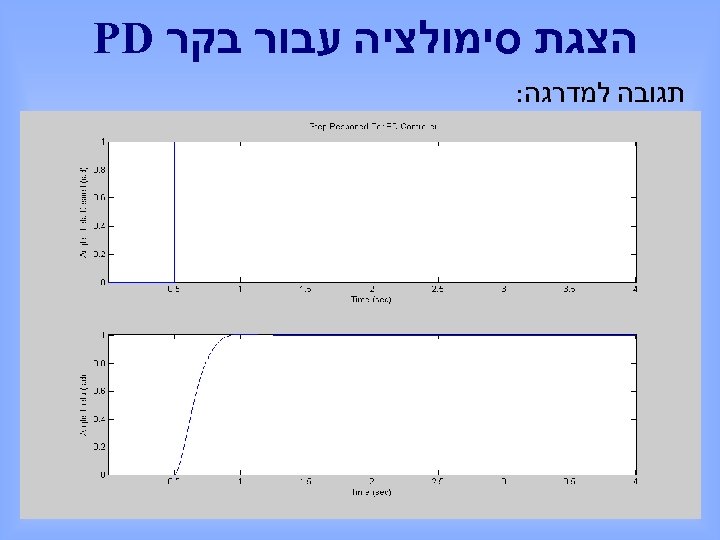
הצגת סימולציה עבור בקר PD תגובה למדרגה:

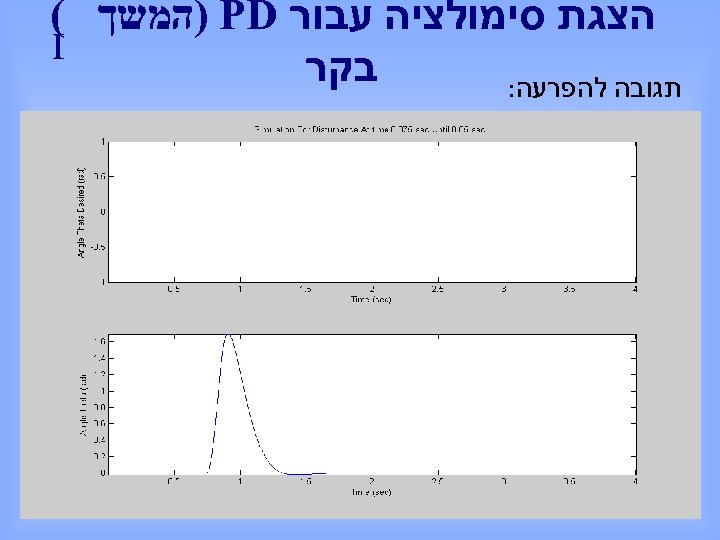
הצגת סימולציה עבור ) PD המשך ( I בקר תגובה להפרעה:

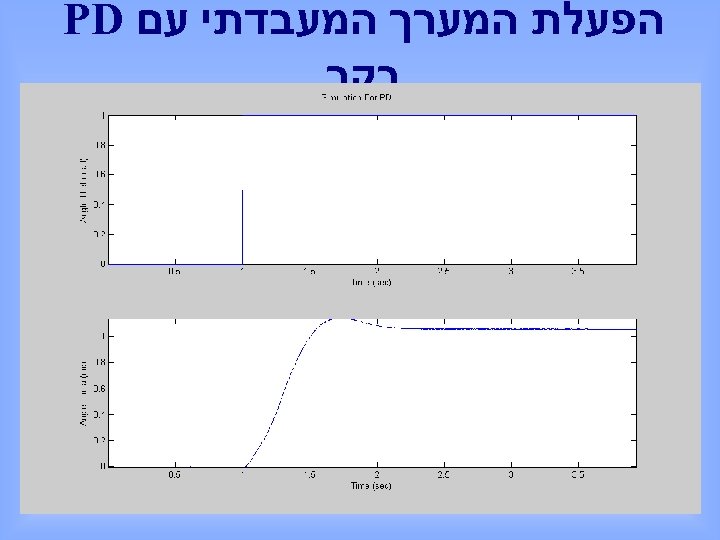
הפעלת המערך המעבדתי עם PD בקר

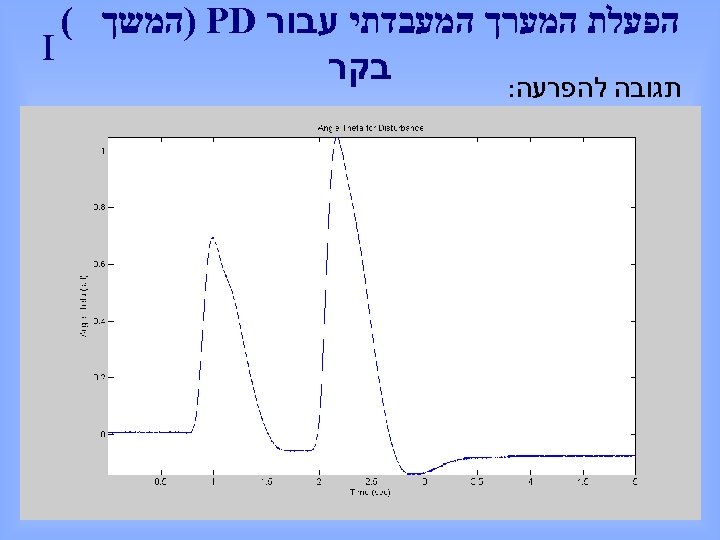
הפעלת המערך המעבדתי עבור ) PD המשך ( I בקר תגובה להפרעה:

הצגת מערך מעבדתי עבור בקר SMC

הצגת מערך מעבדתי עבור בקר PD

הצגת מערך מעבדתי עבור בקר SMC תגובה להפרעה

הצגת מערך מעבדתי עבור בקר PD תגובה להפרעה

תיאור שיטת GSMC הבדל העיקרי של שיטת GSMC לעומת שיטת SMC הינו בתוספת של פונקצית אילוץ ) f(t למשטח . הגלישה - פונקצית האילוץ הינה פונקצית מסלול רצוי למערכת. פונקצית האילוץ מניעה את מצב המערכת מכל מצב במרחב ישירות אל משטח הגלישה ללא שלב הגעה.

תיאור שיטת ) GSMC המשך (I המערכת שלנו עפ"י ע "י . והמשטח מוגדר ע"י : , SMC השגיאה מוגדרת כלומר בהצבת נקבל: . המערכת שלנו עפ"י : , GSMC כאשר הינו ערך הזווית הסופית של הפקודה הרצויה. , המשטח מוגדר ע"י השגיאה מוגדרת ע"י , ו- ) f(t מוגדר ע"י .

תיאור שיטת ) GSMC המשך (II לתוך S נקבל: ובהצבת וקבלנו שתוספת הפונקציה ) f(t למשטח הגלישה מעבירה מידע זהה לזה שמועבר בשיטת SMC ולא מהווה חידוש. יותר הגיונית , ברור שהגדרת השגיאה כ (במידה והחלטנו על הפרופיל , )מאשר הגדרת השגיאה כ- .

סיכום ומסקנות v שיטת בקרת Sliding Mode הינה שיטה המאפשרת ע"י שינוי של מספר פרמטרים מצומצם לשלוט על התגובה של המערכת. v המערכת המבוקרת ע"י בקר Sliding Mode הינה באופן משמעותי יותר קשיחה להפרעות, )כפי שהוצג בסרט(, וכמו כן זמן חזרה מהפרעה יותר מהיר מזה של בקר PD ובו-זמנית ניתן לשלוט בתגובה הרצויה. v יש לציין שקיימת אפשרות לתכן בקר ליניארי כך שיהיה

סיכום ומסקנות )המשך ( I v הפרופיל שבנינו הינו חיוני לתגובת המערכת( , זהו למעשה ביצוע Prefiltering על כניסת המערכת(. חסרונות: v התנהגות "עצבנית" של המערכת , (, (Chattering ביציאת הבקר כתוצאה מפונקצית ה- ). Sign(s v קיים קושי בבקרה על ממאמץ הבקרה הגדול. ניסיון לממש את הבקר המלא על המערך המעבדתי לא בגלל הרעש הנוצר כתוצאה

הטכניון — מכון טכנולוגי לישראל TECHNION —