геометрия.ppt
- Количество слайдов: 7

Қ. И. Сатбаев атындағы Қазақ Ұлттық Техникалық Университеті Сызба геометрия және инженерлік графика кафедрасы Жұмыстың тақырыбы: Негізгі позициялық есептерді тектес сәйкестікпен зерттеу
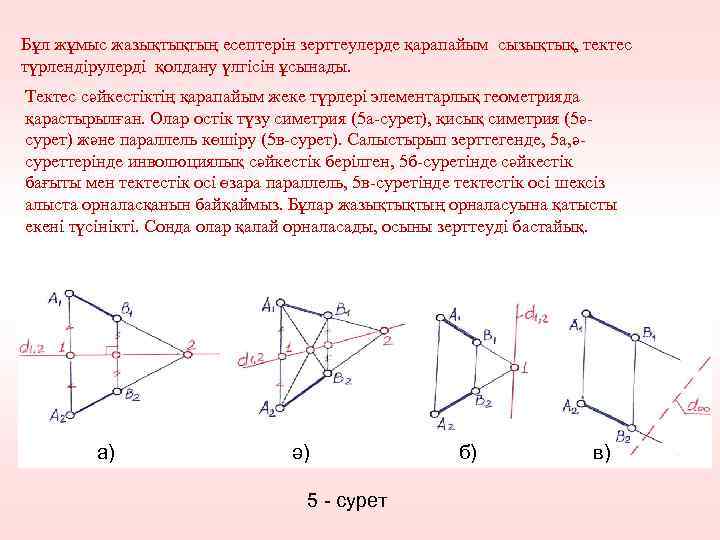
Бұл жұмыс жазықтықтың есептерін зерттеулерде қарапайым сызықтық, тектес түрлендірулерді қолдану үлгісін ұсынады. Тектес сәйкестіктің қарапайым жеке түрлері элементарлық геометрияда қарастырылған. Олар остік түзу симетрия (5 а-сурет), қисық симетрия (5әсурет) және параллель көшіру (5 в-сурет). Салыстырып зерттегенде, 5 а, әсуреттерінде инволюциялық сәйкестік берілген, 5 б-суретінде сәйкестік бағыты мен тектестік осі өзара параллель, 5 в-суретінде тектестік осі шексіз алыста орналасқанын байқаймыз. Бұлар жазықтықтың орналасуына қатысты екені түсінікті. Сонда олар қалай орналасады, осыны зерттеуді бастайық. а) ә) 5 - сурет б) в)
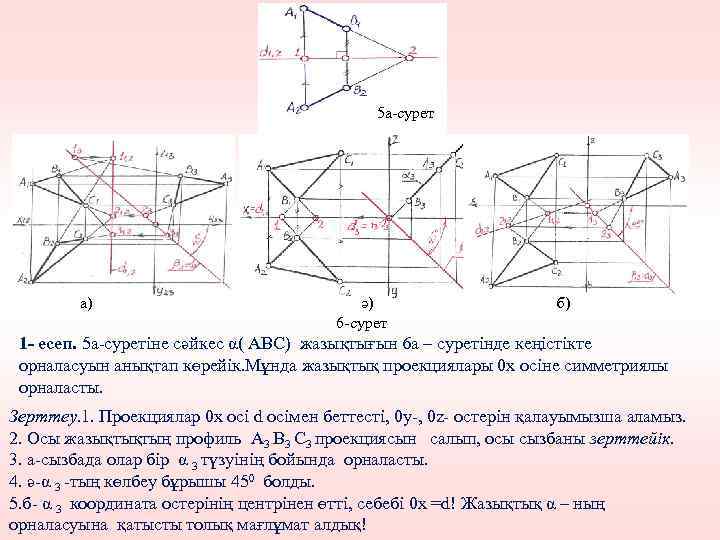
5 а-сурет а) ә) 6 -сурет б) 1 - есеп. 5 а-суретіне сәйкес α( АВС) жазықтығын 6 а – суретінде кеңістікте орналасуын анықтап көрейік. Мұнда жазықтық проекциялары 0 х осіне симметриялы орналасты. Зерттеу. 1. Проекциялар 0 х осі d осімен беттесті, 0 у-, 0 z- остерін қалауымызша аламыз. 2. Осы жазықтықтың профиль А 3 В 3 С 3 проекциясын салып, осы сызбаны зерттейік. 3. а-сызбада олар бір α 3 түзуінің бойында орналасты. 4. ә-α 3 -тың көлбеу бұрышы 450 болды. 5. б- α 3 координата остерінің центрінен өтті, себебі 0 х =d! Жазықтық α – ның орналасуына қатысты толық мағлұмат алдық!
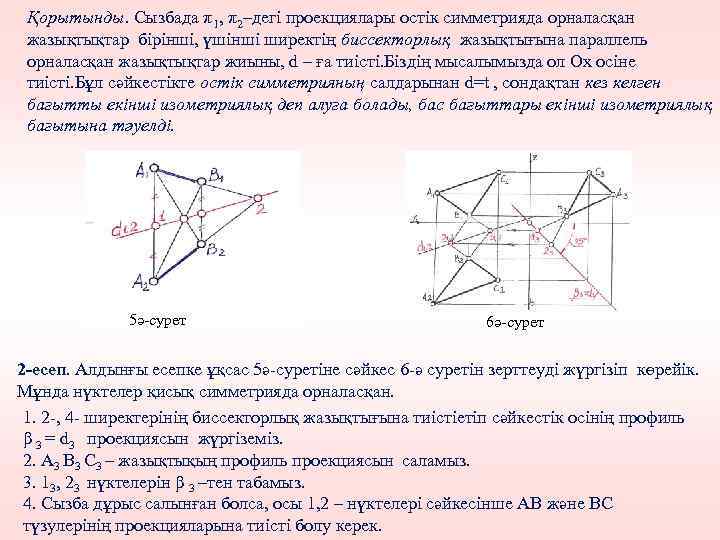
Қорытынды. Сызбада π1, π2–дегі проекциялары остік симметрияда орналасқан жазықтықтар бірінші, үшінші ширектің биссекторлық жазықтығына параллель орналасқан жазықтықтар жиыны, d – ға тиісті. Біздің мысалымызда ол Ох осіне тиісті. Бұл сәйкестікте остік симметрияның салдарынан d=t , сондақтан кез келген бағытты екінші изометриялық деп алуға болады, бас бағыттары екінші изометриялық бағытына тәуелді. 5ә-сурет 6ә-сурет 2 -есеп. Алдынғы есепке ұқсас 5ә-суретіне сәйкес 6 -ә суретін зерттеуді жүргізіп көрейік. Мұнда нүктелер қисық симметрияда орналасқан. 1. 2 -, 4 - ширектерінің биссекторлық жазықтығына тиістіетіп сәйкестік осінің профиль β 3 = d 3 проекциясын жүргіземіз. 2. А 3 В 3 С 3 – жазықтықың профиль проекциясын саламыз. 3. 13, 23 нүктелерін β 3 –тен табамыз. 4. Сызба дұрыс салынған болса, осы 1, 2 – нүктелері сәйкесінше АВ және ВС түзулерінің проекцияларына тиісті болу керек.
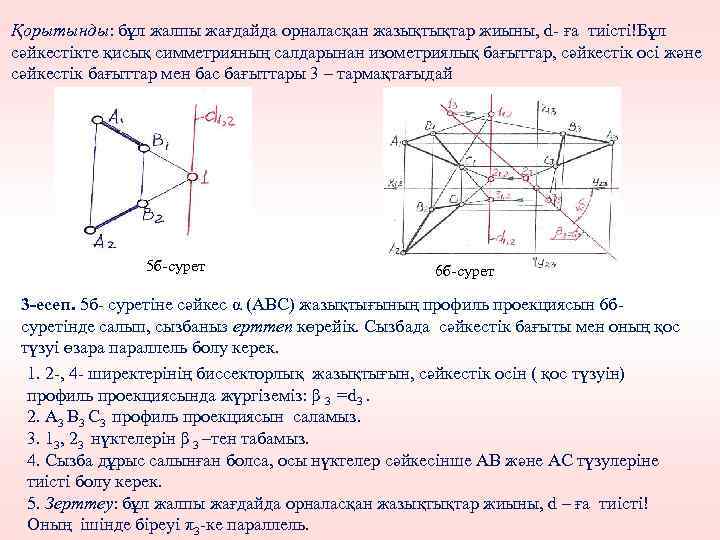
Қорытынды: бұл жалпы жағдайда орналасқан жазықтықтар жиыны, d- ға тиісті!Бұл сәйкестікте қисық симметрияның салдарынан изометриялық бағыттар, сәйкестік осі және сәйкестік бағыттар мен бас бағыттары 3 – тармақтағыдай 5 б-сурет 6 б-сурет 3 -есеп. 5 б- суретіне сәйкес α (АВС) жазықтығының профиль проекциясын 6 бсуретінде салып, сызбаныз ерттеп көрейік. Сызбада сәйкестік бағыты мен оның қос түзуі өзара параллель болу керек. 1. 2 -, 4 - ширектерінің биссекторлық жазықтығын, сәйкестік осін ( қос түзуін) профиль проекциясында жүргіземіз: β 3 =d 3. 2. А 3 В 3 С 3 профиль проекциясын саламыз. 3. 13, 23 нүктелерін β 3 –тен табамыз. 4. Сызба дұрыс салынған болса, осы нүктелер сәйкесінше АВ және АС түзулеріне тиісті болу керек. 5. Зерттеу: бұл жалпы жағдайда орналасқан жазықтықтар жиыны, d – ға тиісті! Оның ішінде біреуі π3 -ке параллель.

Қорытынды. Сәйкестіктің бір изометриялық бағыты – сәйкестік осі. Сәйкестіктің бас бағыттары мен екінші изометриялық бағыты 3 -тармақтағыдай. 5 в-сурет 6 в-сурет 4 - есеп. 5 в- суретіне сәйкес α (АВС) жазықтығын 6 в-суретінде салып, оны зерттеп көрейік 1. Мұнда сәйкестіктің қос түзуі шексіз алыста d∞, түзулердің проекциялары өзара параллель, сондықтан берілген α 3. 1. 2 -, 4 - ширектердің биссекторлық жазықтығының профиль β 3 =d 3∞ проекциясын жүргіземіз. 2. А 3 В 3 С 3 профиль проекциясын саламыз. Бұл түзу сызық болды және ол β 3 –ке параллель. 3. Зерттеу. Тектес осі шексіз алыста, сондықтан тектестікпен берілген α жазықтығы β – ға параллель. Есептің шешуі осы жазықтыққа параллель орналасқан жазықтықтар жиыны, d ∞ -ке тиісті.

Монж эпюрінде қайсыбір берілген жазықтық π1, π2 –жазықтықтардың нүктелері арасында тектес сәйкестілік орнатылады. Осының арқасында жазықтықтарға қатысты барлық позициялық есептерді тектес сәйкестікпен шешуге болады. Сәйкестіктің изометриялық және бас бағыттарын қолданып, сызбада шеңберге сәйкес элліпсті, квадратқа сәйкес ромбты салуға болады. Осындай есептерді зерттеудің нәтижесінде студенттердің геометриялықлогикалық ойлау өрісі кеңейеді, олардың зерттеу жұмыстарына деген қызығушылығы арта түседі.
геометрия.ppt