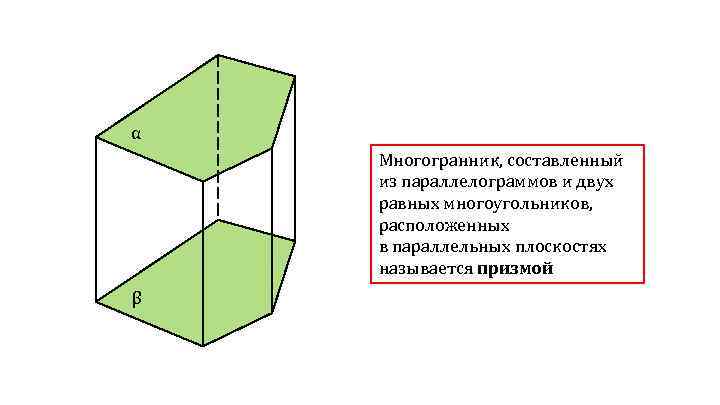
α Многогранник, составленный из параллелограммов и двух равных многоугольников, расположенных в параллельных плоскостях называется призмой β
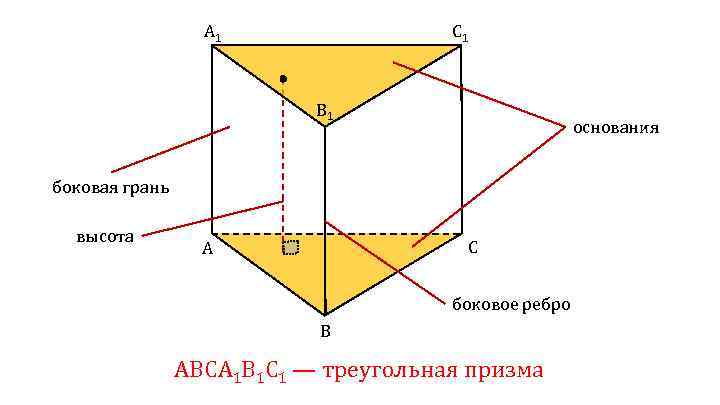
A 1 C 1 B 1 основания боковая грань высота C A боковое ребро B АВСA 1 B 1 C 1 — треугольная призма
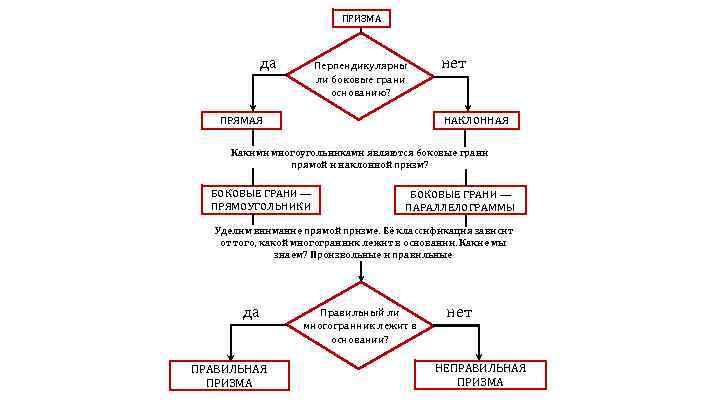
ПРИЗМА да Перпендикулярны ли боковые грани основанию? ПРЯМАЯ нет НАКЛОННАЯ Какими многоугольниками являются боковые грани прямой и наклонной призм? БОКОВЫЕ ГРАНИ — ПРЯМОУГОЛЬНИКИ БОКОВЫЕ ГРАНИ — ПАРАЛЛЕЛОГРАММЫ Уделим внимание прямой призме. Её классификация зависит от того, какой многогранник лежит в основании. Какие мы знаем? Произвольные и правильные да ПРАВИЛЬНАЯ ПРИЗМА Правильный ли многогранник лежит в основании? нет НЕПРАВИЛЬНАЯ ПРИЗМА
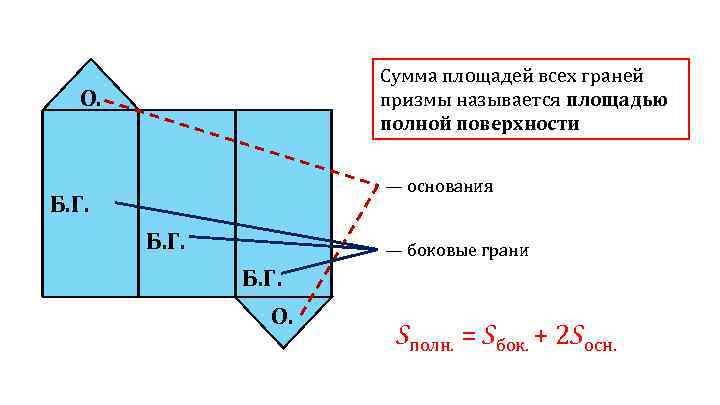
Сумма площадей всех граней призмы называется площадью полной поверхности О. — основания Б. Г. — боковые грани Б. Г. О. Sполн. = Sбок. + 2 Sосн.
Теорема Площадь боковой поверхности прямой призмы равна произведению высоты призмы на периметр её основания Sбок. = a 1 · h + a 2 · h + a 3 · h + … an · h = h a 3 a 1 a 2
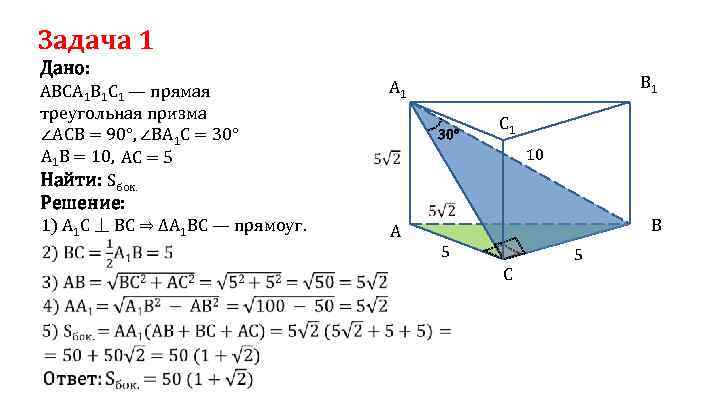
Задача 1 Дано: АВСА 1 В 1 С 1 — прямая треугольная призма ∠AСB = 90°, ∠ВА 1 С = 30° А 1 В = 10, АС = 5 Найти: Sбок. 30° C 1 10 Решение: 1) А 1 С ⏊ ВС ⇒ ΔА 1 ВС — прямоуг. B 1 A 1 B A 5 5 C
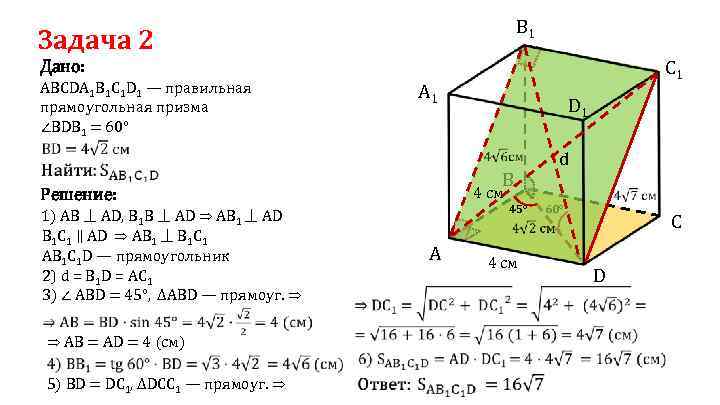
B 1 Задача 2 C 1 Дано: A 1 АВСDА 1 В 1 С 1 D 1 — правильная прямоугольная призма ∠ВDВ 1 = 60° Решение: 1) AB ⏊ AD, B 1 B ⏊ AD ⇒ AB 1 ⏊ AD В 1 С 1 ∥ AD ⇒ AB 1 ⏊ В 1 С 1 AB 1 C 1 D — прямоугольник 2) d = В 1 D = АС 1 3) ∠ ABD = 45°, ΔABD — прямоуг. ⇒ 5) BD = DC 1, ΔDCC 1 — прямоуг. ⇒ B d 4 см 45° 60° C A ⇒ AB = AD = 4 (см) D 1 4 см D
Скачать презентацию α Многогранник составленный из параллелограммов и двух равных
28. Призма.ppt