
§ 3. ОТОБРАЖЕНИЯ МНОЖЕСТВ

О. 1. Бинарное отношение f А В называется отображением множества А в множество В, если δf = А, ρf В и из того, что (х, у1) f и (х, у2) f следует, что у1 = у2. Другими словами, отображением множества А в множество В называется всякое правило f, по которому каждому элементу множества А сопоставляется вполне определенный (единственный) элемент множества В. Обозначение: f: А → В.

Если при этом элементу х А сопоставлен элемент у В, то у называют образом элемента х, а элемент х – прообразом элемента у при отображении f. Обозначение: у = f(х) или хf = у. Из о. 1 у каждого элемента х А образ единственный, однако для элемента у В прообразов может быть много, а может и вообще не быть. Множество всех прообразов элемента у В называется его полным прообразом и обозначается f 1(у):

Каждому подмножеству А 1 множества А соответствует его образ f(А 1) при отображении f, который состоит из всех элементов множества В, являющихся образами какого-нибудь элемента из А 1: Каждому подмножеству В 1 множества В соответствует его полный прообраз f 1(В 1) при отображении f, который состоит из всех элементов, образы которых принадлежат В 1:

Множество А называется областью определения, а множество f(А) – множеством значений отображения f. Замечание Отображение f множества А в множество В называется так же функцией, заданной на множестве А и принимающей значения во множестве В. При этом элемент f(х) называется значением функции f в точке х. Само множество А называется областью определения, а множество f(А) В – областью значений функции f.

О. 2. Отображение f: А → В называется сюръективным или отображением А на В, если каждый элемент у В является образом хотя бы одного элемента х А, т. е. f(А) = В. Обозначение сюръекции: В этом случае для любого у В: f 1(у) . О. 3. Отображение f: А → В называется инъективным (1 -1 функцией, вложением), если оно разные элементы множества А отображает в разные элементы множества В, т. е. f(х1) = f(х2) х1 = х2.

Обозначение инъекции: В этом случае для любого у В: f 1(у) либо пустое, либо одноэлементное множество. О. 4. Отображение f: А → В называется биективным или взаимно однозначным отображением А на В, если оно сюръективно и инъективно. Обозначение биекции: f: А В. В этом случае для любого у В: f 1(у) одноэлементное множество.
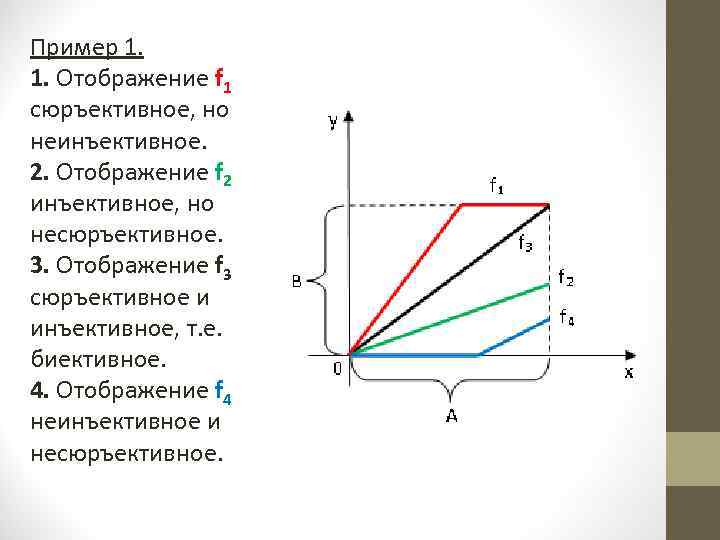
Пример 1. 1. Отображение f 1 сюръективное, но неинъективное. 2. Отображение f 2 инъективное, но несюръективное. 3. Отображение f 3 сюръективное и инъективное, т. е. биективное. 4. Отображение f 4 неинъективное и несюръективное.

О. 5. Отображение множества А в себя называется преобразованием множества А. О. 6. Биективное преобразование множества А называется подстановкой множества А или подстановкой на А. Пример 2. Примером подстановки на множестве целых чисел Z может служить отображение f: Z → Z, определяемое равенством f(х) = х +1, х Z.

О. 7. Композицией отображений φ: В → С и f: А → В называется отображение φ ◦ f: А → С, определяемое равенством (φ ◦ f)(х) = φ(f(х)), х А. Свойства композиции отображений Свойство 1. Если f 1: А → В, f 2: В → С, f 3: С → D, то (f 3 ◦ f 2) ◦ f 1 = f 3 ◦ (f 2 ◦ f 1). Свойство 2. Если отображения f 1: А → В и f 2: В → С сюръективны, инъективны или биективны, то соответственно таким же будет и отображение f 2 ◦ f 1.

Свойство 3. Если для отображений f: А → В, φ: В → С и ψ: В → С выполняется равенство φ ◦ f = ψ ◦ f и отображение f сюръективно, то φ = ψ. Свойство 4. Если для отображений f: А → В, φ: А → В и ψ: В → С выполняется равенство ψ ◦ φ = ψ ◦ f и отображение ψ инъективно, то φ = f. Свойство 5. Если f и φ – преобразования множества А, то их композиция f ◦ φ так же является преобразованием множества А.