ef2f8f110c848463267d7aba16e30d1d.ppt
- Количество слайдов: 122

視覚情報処理論 ・ 三次元画像処理特論

概要 n n 画像ベース物体認識に関する最近の論文 先週の復習:物体認識の考え方 指標の連続(可微分)化 今週のテーマ n n n 階層化による物体認識 物体輪郭線の抽出への応用 深層学習の例

前回の復習 n 物体認識とは? n 物体認識の基本的な考え方 n 近年の傾向

物体認識とは? 古典的な定義 「あらかじめ与えられた物体Aが、入力画 像Xの中に存在するか否か、存在するとす ればどこにあるか、を自動的に決定するこ と」 n 究極の問題(未解決) 「入力画像Xのみを与えて、そのXがどうい う画像であるかを自動的に決定すること」 n

古典的な問題の例 n この車は何だ? n あらかじめ教えた車のどれだ?

究極問題の例 n これは何だ? n 一般道、片側4車線、左側通行、分離帯、信号交差点…

物体認識の基本的な考え方 n お手本からモデル(群)を作る 入力画像から似たモデルを探す n いいモデルの作り方 n n n 似た物体からは似たモデル モデルの類似性の評価

特定物体の認識とクラス認識 n 特定(複数でも可)モデルの認識 n n 前述のモデルを他と区別して認識 クラス認識 n n n 前述のモデルで「似ているもの」を一まとめ そのまとまり(クラスタ)のうちで似ているもの 現在の主流(1つしか対象がないものが個別)

近年の画像認識用モデル n 認識対象物体から「局所特徴」を抽出 n n 局所的には類似度が高い 物体全体が見えないこともある どこにあるかわからないことが多い 「局所特徴」の組み合わせで評価 n n n 組み合わせは膨大 認識には「遊び」がある 複数クラスにも応用可能

パッチベースの物体認識 n データベースを作る(事前に用意) n n お手本を用意する(近年は大量に) 局所特徴の組み合わせ(モデル)を作る 組み合わせを決めるとクラスが決まるように データベースを探索(認識時) n n n 入力画像から局所特徴の組み合わせを計算 組み合わせに近いクラスを検出 必要なら組み合わせから位置を推定
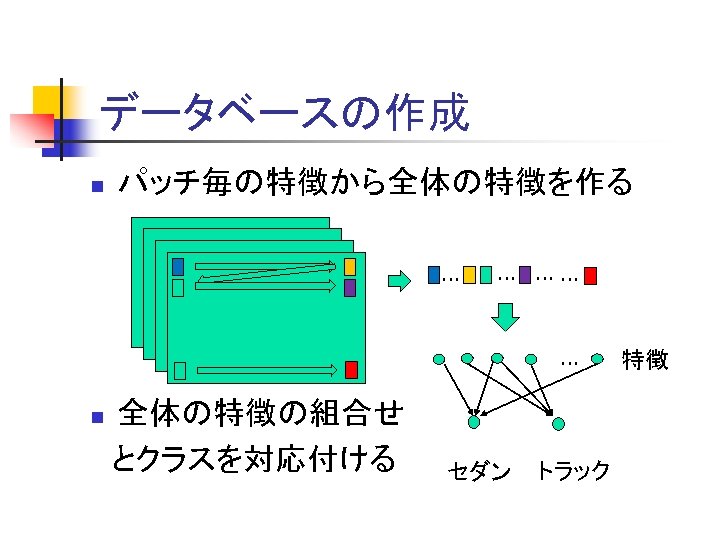
データベースの作成 n パッチ毎の特徴から全体の特徴を作る … … …… … 全体の特徴の組合せ とクラスを対応付ける n セダン トラック 特徴
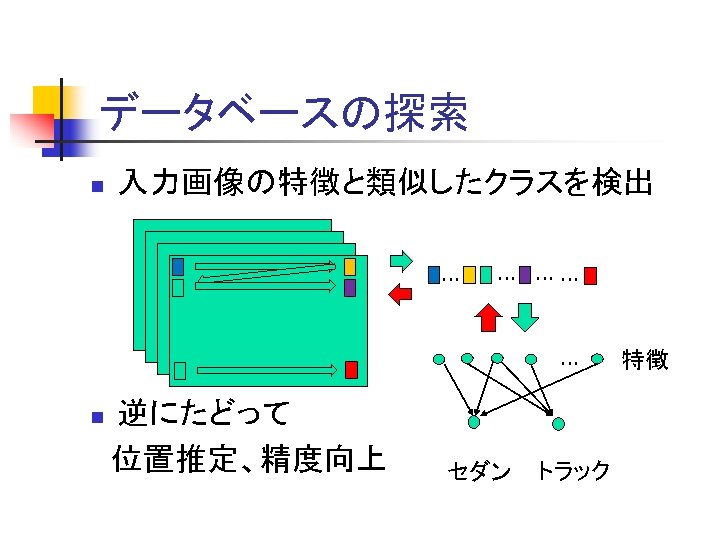
データベースの探索 n 入力画像の特徴と類似したクラスを検出 … … …… … 逆にたどって 位置推定、精度向上 n セダン トラック 特徴

特徴づけの部分 n 素朴な方法(Yes/No question) A B C D セダン … Z 特徴 トラック セダン=A∧¬B∧C∧…∧Z =a*(1 -b)*c*…*z (a, . . , z: 0 or 1) P(セダン)=f(a, b, c, …, z) とかける n

指標の連続(可微分)化(1) n 実際の特徴は、単純にYES/NOではない n n プロジェクタは娯楽に使うか? たくさんのYESがありうる n リンゴなら、多くの場所が赤いだろう
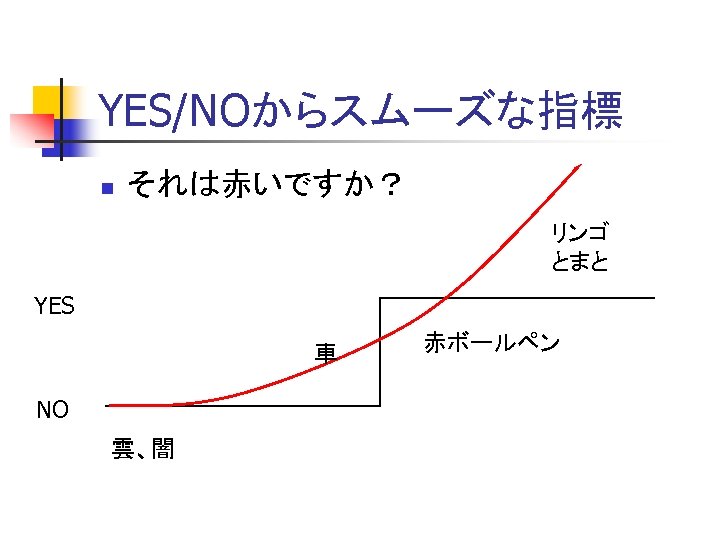
YES/NOからスムーズな指標 n それは赤いですか? リンゴ とまと YES 車 NO 雲、闇 赤ボールペン
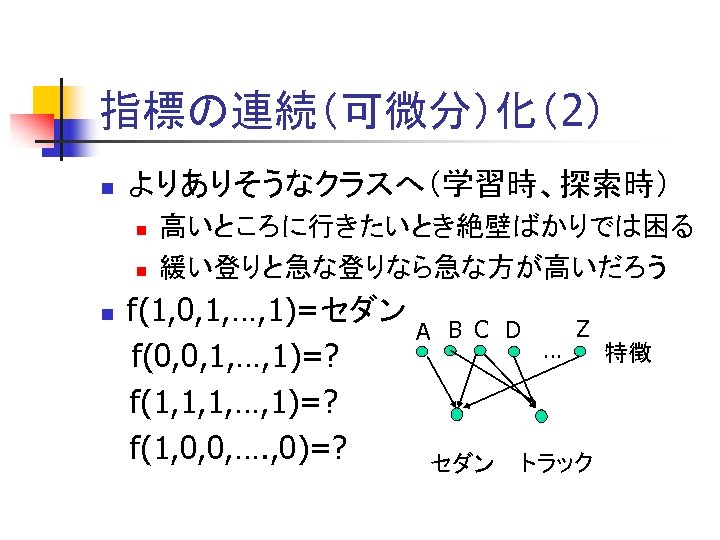
指標の連続(可微分)化(2) n よりありそうなクラスへ(学習時、探索時) n n 高いところに行きたいとき絶壁ばかりでは困る 緩い登りと急な登りなら急な方が高いだろう f(1, 0, 1, …, 1)=セダン f(0, 0, 1, …, 1)=? f(1, 1, 1, …, 1)=? f(1, 0, 0, …. , 0)=? n A B C D セダン … Z トラック 特徴
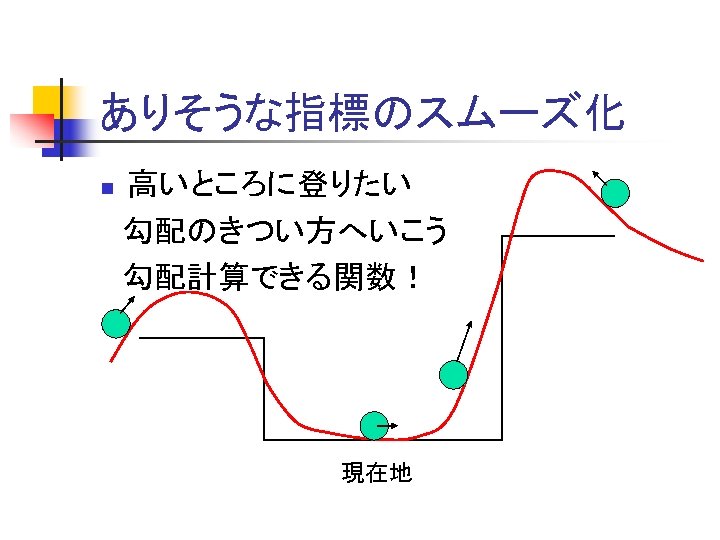
ありそうな指標のスムーズ化 高いところに登りたい 勾配のきつい方へいこう 勾配計算できる関数! n 現在地
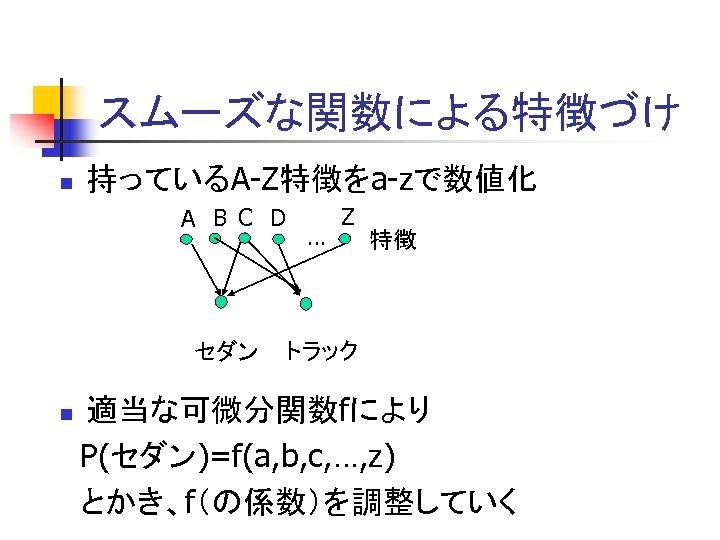
スムーズな関数による特徴づけ n 持っているA-Z特徴をa-zで数値化 A B C D セダン … Z 特徴 トラック 適当な可微分関数fにより P(セダン)=f(a, b, c, …, z) とかき、f(の係数)を調整していく n
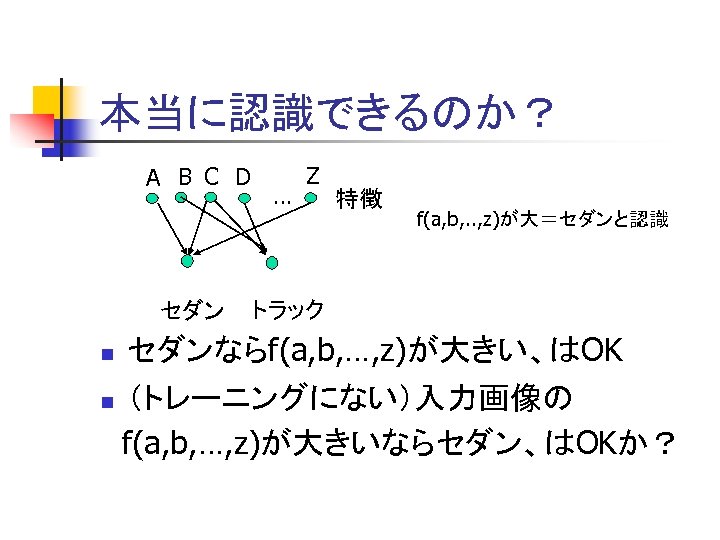
本当に認識できるのか? A B C D … Z 特徴 f(a, b, . . , z)が大=セダンと認識 セダン トラック n セダンならf(a, b, …, z)が大きい、はOK n (トレーニングにない)入力画像の f(a, b, …, z)が大きいならセダン、はOKか?
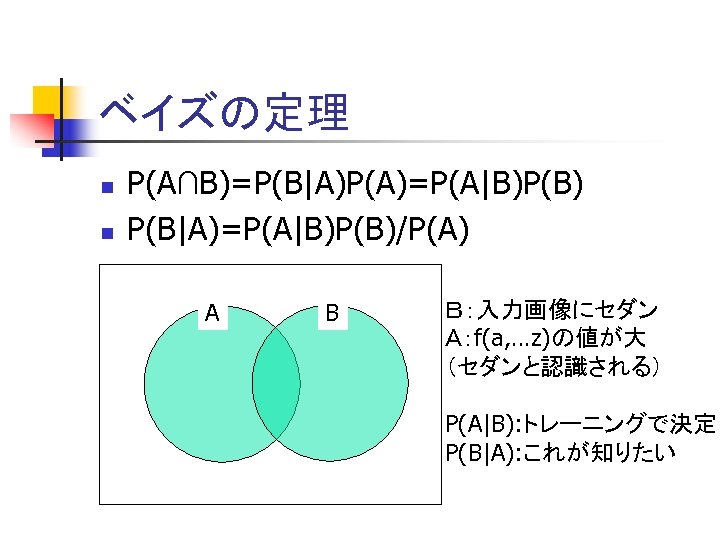
ベイズの定理 n n P(A∩B)=P(B|A)P(A)=P(A|B)P(B) P(B|A)=P(A|B)P(B)/P(A) A B B:入力画像にセダン A:f(a, …z)の値が大 (セダンと認識される) P(A|B): トレーニングで決定 P(B|A): これが知りたい

事後確率で物体認識は可能 P(B|A)=P(A|B)P(B)/P(A)より n P(B|A)∝P(A|B) B: セダンがある、 A: fの値が大きい n P(B)≒P(A) となるような出来のいい f P(B|A)≒P(A|B) n 画像内にセダンがあるかどうかはfの大小 で判断してもよい! n
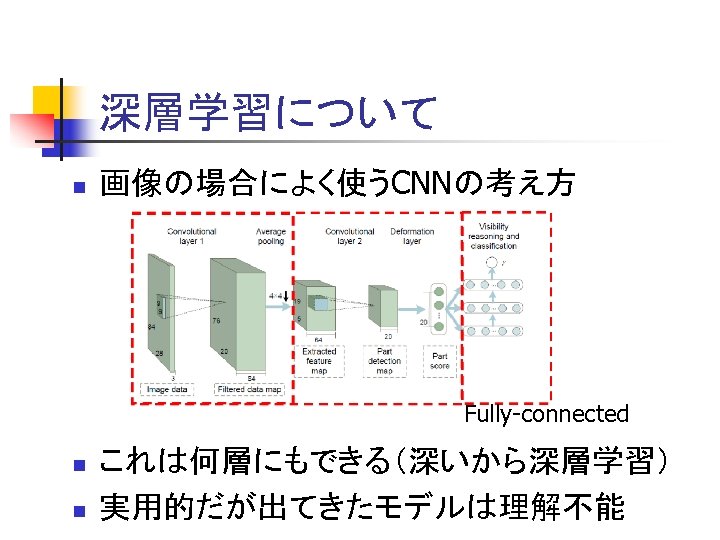
深層学習について n 画像の場合によく使うCNNの考え方 Fully-connected n n これは何層にもできる(深いから深層学習) 実用的だが出てきたモデルは理解不能

最初の論文 n Semantic Hierarchies for Recognizing Objects and Parts n Boris Epshtein Shimon Ullman Weizmann Institute of Science, ISRAEL n CVPR 2007 n

概要 n パッチベースのクラス認識 n 階層化 n 多数の画像から自動的に階層化する手法 n 実験
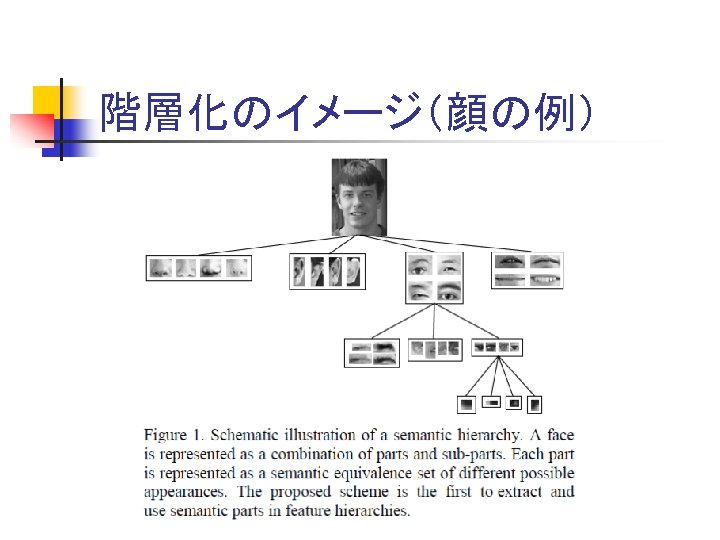
階層化のイメージ(顔の例)
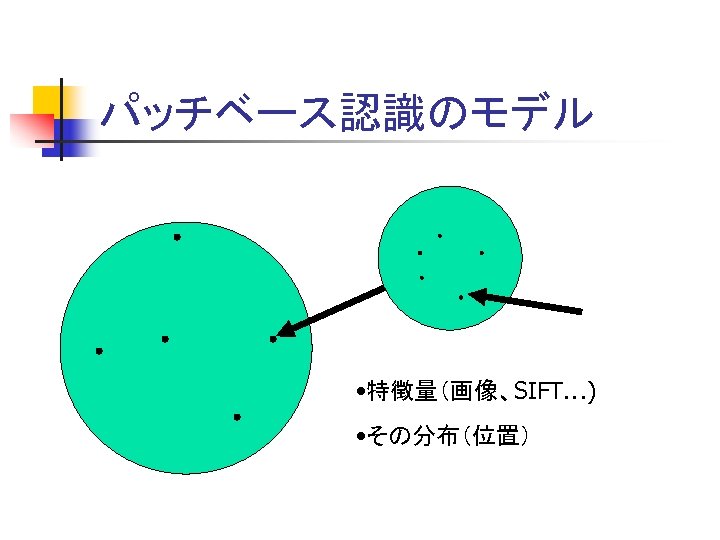
パッチベース認識のモデル • 特徴量(画像、SIFT…) • その分布(位置)

意味階層(理論部分) n 「樹形図」モデル n 分類とパーツ(パッチ)の解釈 n 階層の構築 n トレーニング手法
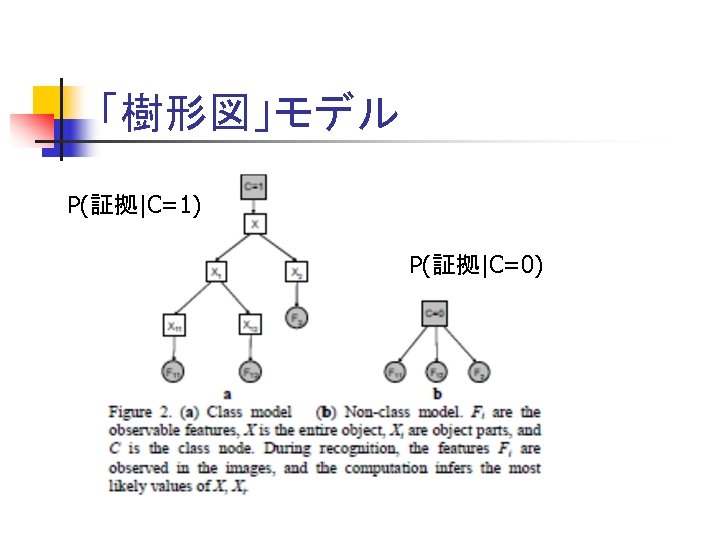
「樹形図」モデル P(証拠|C=1) P(証拠|C=0)

クラスのモデル n n Xは階層構造 Xi, Xijk などからなる 各XIは A(XI), L(XI)を変数にもつ A(XI)はパーツXIの見え具合 1なら開いた口、2なら閉じた口等 n L(XI)はパーツXIの存在する場所 L(XI)=0はパーツXIが見えないことを意味 n 場所は中心(x, y)がどのピクセルかを示す n n XI :末端→画像特徴量ベクトルFIが対応
![末端部分について n n XI :末端→特徴量ベクトルFIが対応 FIは、Nx. K次元ベクトル空間の点 (S[1, 1], …, S[1, N], …, S[K, 末端部分について n n XI :末端→特徴量ベクトルFIが対応 FIは、Nx. K次元ベクトル空間の点 (S[1, 1], …, S[1, N], …, S[K,](https://present5.com/presentation/ef2f8f110c848463267d7aba16e30d1d/image-30.jpg)
末端部分について n n XI :末端→特徴量ベクトルFIが対応 FIは、Nx. K次元ベクトル空間の点 (S[1, 1], …, S[1, N], …, S[K, 1], …, S[K, N]) とみなす S[i, j]のiは、XIの見えの変化、Nは位置に対応 n Xiが起こりうる(意味、位置)のすべての場合にF との類似度を与える

計算したいこと {F}: 入力画像中の特徴量 n p(X|{F})=? (大きければXあり) n P(X|{F})=P({F}|X)P(X)/P({F}) ∝P({F}|X)P(X) なので、P(X), P({F}|X)を計算 n
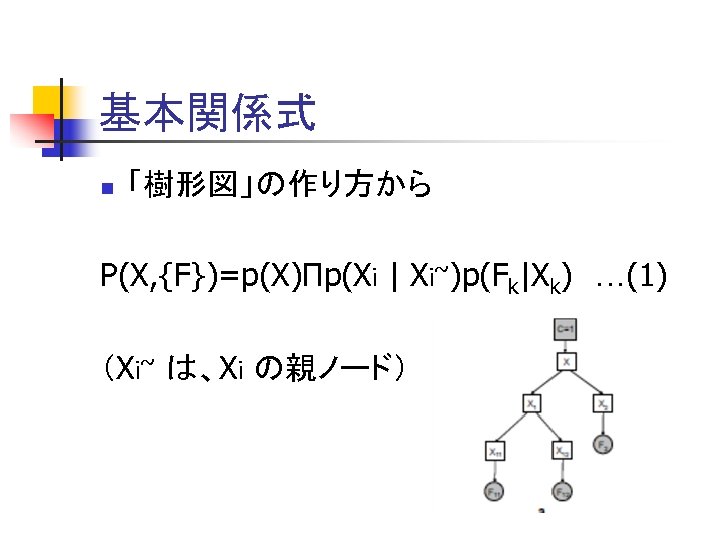
基本関係式 n 「樹形図」の作り方から P(X, {F})=p(X)Πp(Xi | Xi~)p(Fk|Xk) …(1) (Xi~ は、Xi の親ノード)

P(X)の計算 n P(A(X)=a, L(X)=l) クラス番号aの物体が位置lにある確率 n ここでは一様(a, lによらず一定)とする n 顔の証明写真ならl によりますが、本論文 ではこう仮定しています
![P(Fi|A(Xi)=a, L(Xi)=l)の計算(1) Xiが番号a, 位置lにある時、特徴量Fiが観測 される確率 n Fは(S[1, 1], …, S[N, K])と書くのだったから P(Fi|A(Xi)=a, L(Xi)=l) =p(S[1, P(Fi|A(Xi)=a, L(Xi)=l)の計算(1) Xiが番号a, 位置lにある時、特徴量Fiが観測 される確率 n Fは(S[1, 1], …, S[N, K])と書くのだったから P(Fi|A(Xi)=a, L(Xi)=l) =p(S[1,](https://present5.com/presentation/ef2f8f110c848463267d7aba16e30d1d/image-34.jpg)
P(Fi|A(Xi)=a, L(Xi)=l)の計算(1) Xiが番号a, 位置lにある時、特徴量Fiが観測 される確率 n Fは(S[1, 1], …, S[N, K])と書くのだったから P(Fi|A(Xi)=a, L(Xi)=l) =p(S[1, 1], …, S[N, K]| A(Xi)=a, L(Xi)=l)…(2) =Πp(S[k, n]| A(Xi)=a, L(Xi)=l) n Fの各成分は独立と仮定 n
![P(Fi|A(Xi)=a, L(Xi)=l)の計算(2) n 見え方と位置は独立のはず n n 番号aの見えとの一致度分布を Ph(S[a]) 番号aの見えとの不一致度分布 Pm(S[a]) p(S[1, 1], …, S[N, P(Fi|A(Xi)=a, L(Xi)=l)の計算(2) n 見え方と位置は独立のはず n n 番号aの見えとの一致度分布を Ph(S[a]) 番号aの見えとの不一致度分布 Pm(S[a]) p(S[1, 1], …, S[N,](https://present5.com/presentation/ef2f8f110c848463267d7aba16e30d1d/image-35.jpg)
P(Fi|A(Xi)=a, L(Xi)=l)の計算(2) n 見え方と位置は独立のはず n n 番号aの見えとの一致度分布を Ph(S[a]) 番号aの見えとの不一致度分布 Pm(S[a]) p(S[1, 1], …, S[N, K]| A(Xi)=a, L(Xi)=l) =ph(S[a, l])ΠPm(S[k, n]) (k≠a, n≠l)…(3) p(S[1, 1], …, S[N, K]| L(Xi)=0) = ΠPm(S[k, n]) …(4) ; aに依存しない
![P(Fi|A(Xi)=a, L(Xi)=l)の計算(3) P(Fi|A(Xi)=a, L(Xi)=l) ∝ P(Fi|A(Xi)=a, L(Xi)=l) /P(Fi|L(Xi)=0) …(5) =ph(S[a, l])/Pm(S[a, l]) P(Fi|A(Xi)=a, L(Xi)=l)の計算(3) P(Fi|A(Xi)=a, L(Xi)=l) ∝ P(Fi|A(Xi)=a, L(Xi)=l) /P(Fi|L(Xi)=0) …(5) =ph(S[a, l])/Pm(S[a, l])](https://present5.com/presentation/ef2f8f110c848463267d7aba16e30d1d/image-36.jpg)
P(Fi|A(Xi)=a, L(Xi)=l)の計算(3) P(Fi|A(Xi)=a, L(Xi)=l) ∝ P(Fi|A(Xi)=a, L(Xi)=l) /P(Fi|L(Xi)=0) …(5) =ph(S[a, l])/Pm(S[a, l])

p(A(Xi), L(Xi)|A(Xi~), L(Xi~)) P(X, {F})=p(X)Πp(Xi | Xi~)p(Fk|Xk) …(1) だったので、あと残ったのはp(Xi | Xi~) 見えと位置は独立として計算 p(A(Xi), L(Xi)|A(Xi~), L(Xi~)) = p(A(Xi)|A(Xi~))p(L(Xi), L(Xi~)) …(6) n n 第1項と第2項を計算

p(A(Xi)|A(Xi~))の計算 n n n 親が分かっている時にどんな子供がでてく るか、という確率 計算では求まらないのでトレーニングで( 実験的に)求める(方法は後述) 「事前」確率なので教師画像を与えながら 実験的に求めることができる

p(L(Xi), L(Xi~))の計算 n n 親の位置が既知の時、子の位置の分布 L(Xi~)=0の時(親が見えないとき) n n n L(Xi~)≠ 0の時(親が見えるとき) n n n 位置は一様と仮定(一様にδ 0/(N*K)) 1 - δ 0がL(Xi)=0の確率 1 - δ 1がL(Xi)=0の確率 和がδ 1になるように既知の位置関係を正規分 布(ガウス分布)と仮定 δたちはトレーニングで決める

クラス分類とパーツ解釈 n p(C=1|F)を評価したい n n n P(C=1|F)/p(C=0|F) =P(F|C=1)P(C=1)/(P(F|C=0)P(C=0)) ∝P(F|C=1)/P(F|C=0) ボトムアップ トップダウン

ボトムアップ n n n P(F|C=0)は定数なので、P(F|C=1)を計算 これをボトムアップで計算 ノードXi 以下のサブツリーのevidence F(Xi)
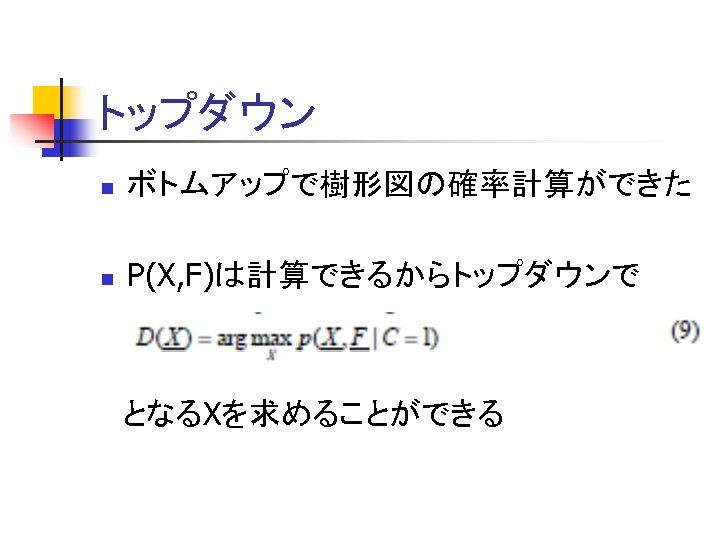
トップダウン n ボトムアップで樹形図の確率計算ができた n P(X, F)は計算できるからトップダウンで となるXを求めることができる

階層構築 n 単純階層(1つの画像から) n 各ノードでの意味づけ(他の画像を追加) n ノードを必要なら階層化

階層構造の例
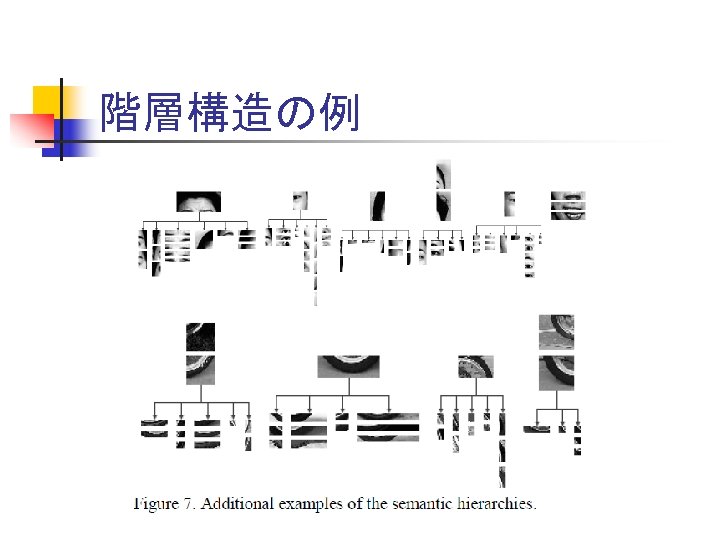
階層構造の例

単純階層 n 特徴量の集中部分を必要に応じて階層化 n 利用する画像は 1枚(または少数)

ノードでの意味づけ(1) n T={Tn|n=1, 2, …} トレーニング画像 多数の画像からノードに意味をもたせる! 各Tnに対し H(X)=D(X)=arg max p(X, F|C=1) を計算 n L(Xi)=0 or ≒ 0かつL(Xi~)≠ 0の時、 L(Xi)=arg max p(L(Xi)|L(Xi~)) 見えは位置L(Xi)のものをとる n

ノードでの意味づけ(2) n n 今の作業をくりかえす 各ノードでほとんど見えないものリストができる そのなかで孤立している見え(周囲にk以上類 似のものがないもの)はとり除く 各ノードで一番効率のよい「見え」を探して、 ノードの見えとして追加する

ノードでの意味づけ(3) n 新たな見えを加えてノードを階層化 n 他のノードの見えと似ている部分があって も階層化により区別可能

トレーニング n n 確率計算時に必要としたパラメータを取得 初期値設定 親子の位置:元々の差、分散はその半分 δは 0. 001 P(A(Xi)|A(Xi~))は、実数をカウント n n トレーニング画像に対してH(X)を求め、最 適になる{Xi}を探し、パラメータに反映 これを繰り返す

実験 n クラス認識 n パーツ検出

クラス認識
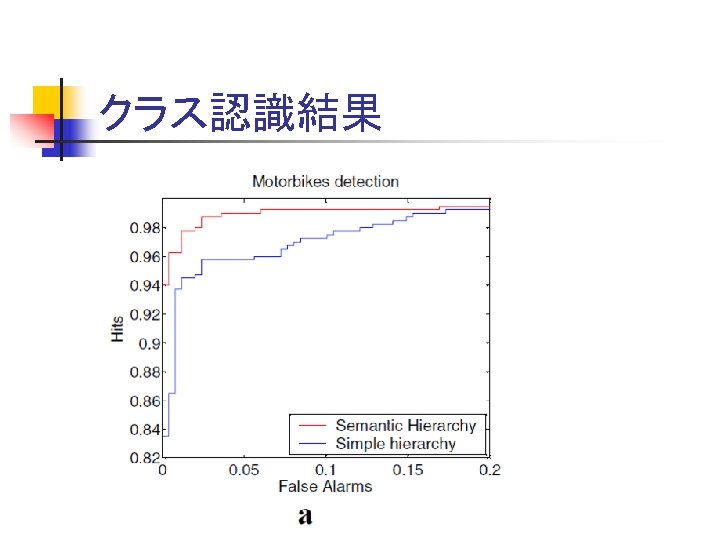
クラス認識結果
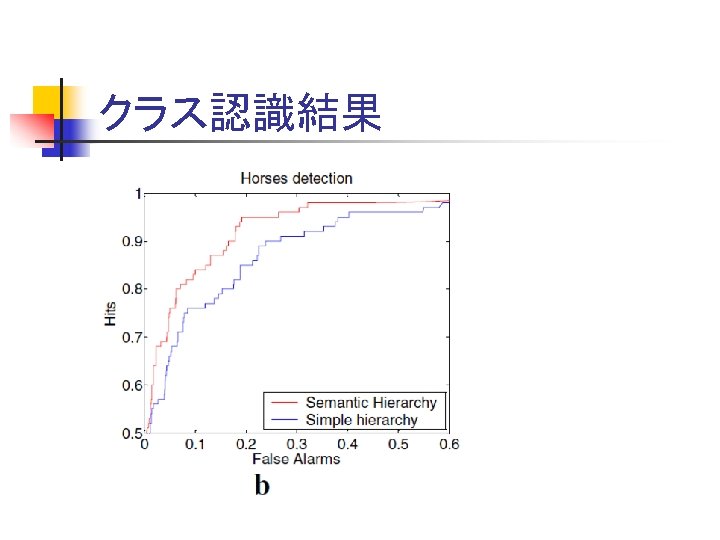
クラス認識結果
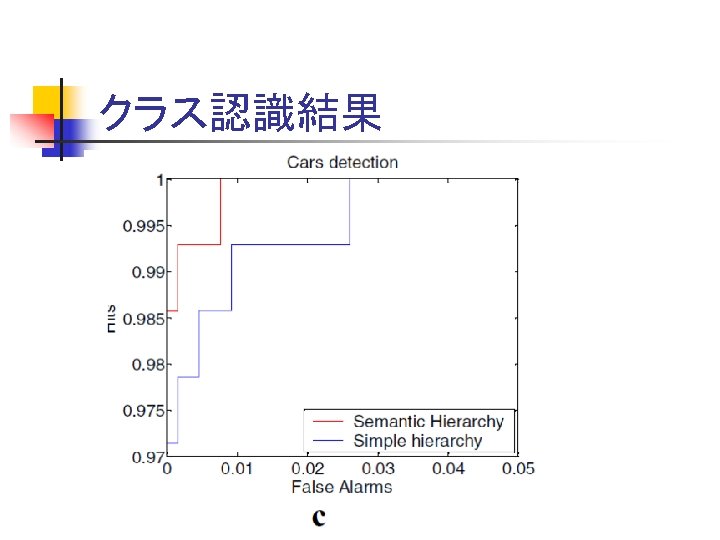
クラス認識結果
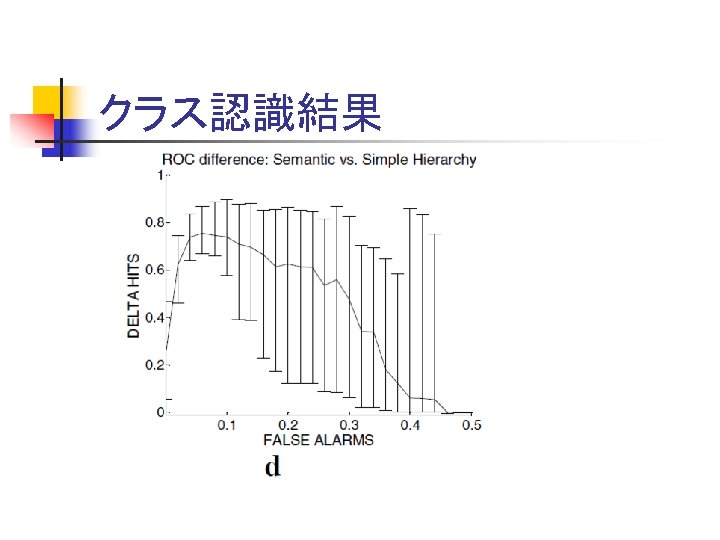
クラス認識結果

パーツ検出

パーツ検出

まとめ n 意味づけ階層化 n n いろんな種類のパーツが認識できる 複雑になればパーツをさらに階層化 n 単純な階層化よりはよい結果 n 複雑な場合でもクラスモデルを自動生成

次の論文 n Accurate Object Localization with Shape Masks n Marcin Marszaek Cordelia Schmid INRIA, LEAR - LJK n CVPR 2007 n

概要 n 物体(クラス)の輪郭線を抽出 n n n クラス認識の副産物(クラス認識はイマイチ) 条件が悪い画像でもOK 物体部分を「マスク」で表現 n マスクは 0, 1でなく 0 -1の確率

結果(一部)

認識対象画像の例

目次 n 要素技術 n n フレームワーク n n マスク間の距離(類似度)の計算 トレーニング手法 認識手法 実験 まとめ

要素技術 n 顕著な局所特徴量と位置合わせ n n n 輪郭マスク n n 局所特徴量 特徴量を用いた物体の位置合わせ マスクの類似度 SVMによるマスクの分類

顕著な局所特徴量と位置合わせ n 局所特徴量 n n n 平行移動、回転、スケール不変等 スケール不変で「正規化」 局所特徴量を用いた物体の位置合わせ n n 局所特徴量が同じ部分が同一 画像1の特徴量θを正規化する変換 p 1 画像2の特徴量θを正規化する変換 p 2 θを介した物体の位置合わせ P 12=p 1 -1 p 2
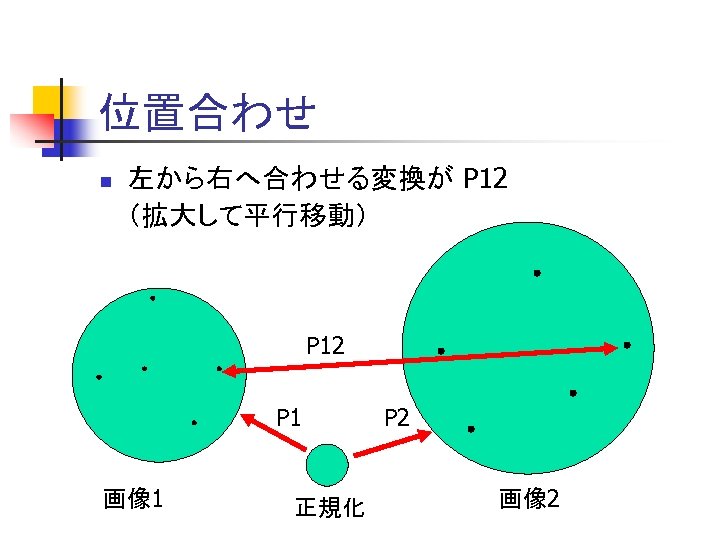
位置合わせ n 左から右へ合わせる変換が P 12 (拡大して平行移動) P 12 P 1 画像 1 正規化 P 2 画像 2

輪郭マスク n 2値マスクの類似度 n 確率マスクの類似度 n 位置合わせした類似度

SVMによるマスクの分類 n n 輪郭線内部の見えを分類 内部→Hi={Hij}を特徴量jの数として定義 n n 特徴量とは局所的な見え方に相当 局所的な見えはV個しかないとみなす 画像に対しV-次元ベクトル空間の点を対応 20 Q方式で Hi をクラス分け n SVM(Support Vector Machine)という効率よ い質問を決定

SVMによるマスクの分類 n Hi と Hjの距離(類似度)は次で定義 ただし、定数Aはすべての D(Hi, Hj)の平均

要素技術終わり n 2つの輪郭線マスクの類似度 n 2つのマスク内部の見えの類似度 n 以上を元にトレーニングと認識を行う

フレームワーク n トレーニング n 認識
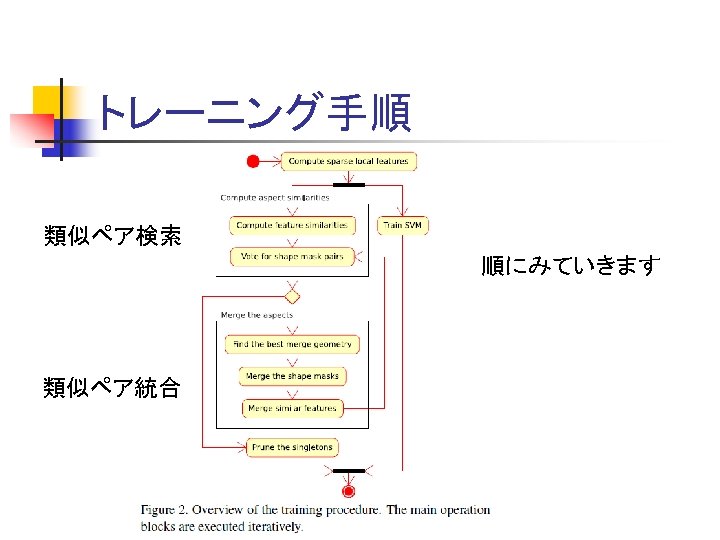
トレーニング手順 類似ペア検索 順にみていきます 類似ペア統合

1. 特徴量抽出 n n V個のどれに相当するか20 Q(SVM)で決定 トレーニング画像では物体領域は既知 n n n 物体の中にない特徴量は捨てる 物体内部の特徴量(i)は正規化変換パラメータ (pi)も記録 Pij(i, jを合わせる変換)が計算可能

2. 特徴の類似性 n 2つのマスクが似ているとは n n n マスクの輪郭線が似ている 局所特徴量が位置も含めて似ているものの探し方 n n n 局所特徴量i, j が似ている時Pijで位置合わせ マスクの類似度が0. 85以上なら「似ている」 類似局所特徴量すべての組み合わせを行う

3. 輪郭線マスクの投票 n n 2の方法ではあまりにも膨大な組合せ 輪郭線マスクの全てのペア(x, y)について n n 2. の方法でどれかの i, j でx, yが類似すれば点 (x, y)に1票投票する 局所特徴量が位置も含め似ていれば投票が 大きくなる 最も似ているペア(x, y)を統合(後述) 統合できなくなるまで繰り返す

投票のしかけ

4. 統合マスクの位置合わせ n n 統合する2つのマスクの位置合わせ 全ての同一特徴量ペア(i, j)について n n n Pijにより2つのマスクを位置合わせ 類似度を以下で計算 最も類似度の大きいもののPijを採用

5. マスクの統合 n n n より「大きい」マスクをベースに統合 4. で決めたPijで位置合わせ 重みつき平均で統合 n n 詳細は書いてないが、常識的にはそれまで統 合してきたマスクの数に比例して統合 見かけが変わったので輪郭マスク距離を 再計算(統合マスクを含むものだけ)

6. 局所特徴量の統合 n n 5. の結果、似ているものを統合 マスク内部の見えも(位置も含め)似ている 場合が多いと考えられる マスクの場合と同様重みつき平均で局所 特徴量を統合 統合したら、また類似ペアを探しに行く

7.Singleton 除去 n 統合処理が終わった後、どれとも統合され なかった画像(マスクとその内部のペア)を singleton という n このような「特殊な」ものは除去してしまう

8. SVM をトレーニング n n 平行して SVM (20 Qの効率的な質問)をト レーニング SVM は物体のクラスごとにトレーニング n n 本当は見かけ毎にトレーニングした方がいい 1つの見かけのサンプルが少なかった
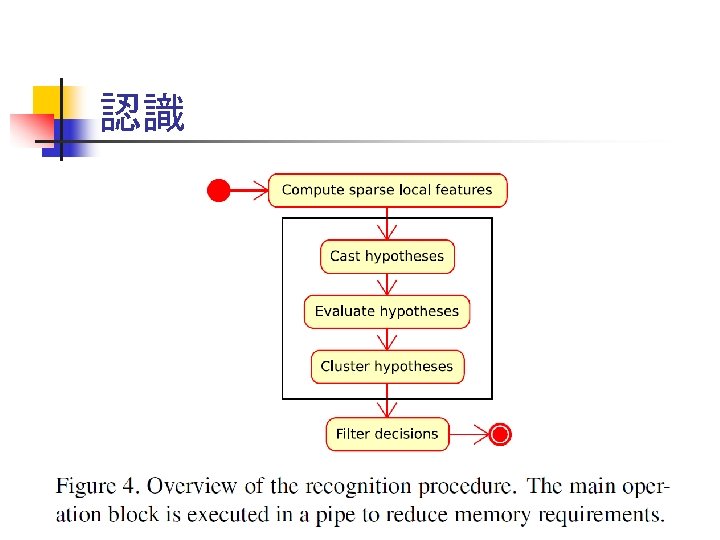
認識

認識のフレームワーク

1. 局所特徴量の計算 n 局所特徴量を計算し、SVMでもっとも近い ものとみなす n 世の中の局所特徴量はV個しかないとする

2. 仮説選出 n n 入力画像の局所特徴量i トレーニングしたマスクの局所特徴量j n Pijで位置合わせ n どの位置にどんなマスクがあるかの仮説 n もちろん、これでは仮説が多すぎる!

3. 仮説評価 n n n 入力画像から切り取ったマスクエリアからH をとりだす HもSVMで分類してあった 内部の「自信」度が計算できる

仮説評価

4. 仮説「統合」 n 一部隠れると自信が減る n n 多くの輪郭線マスク仮説 n n 局所特徴量の見えと位置で補強 統合の必要性(100以上は統合するとか) 類似度の高い仮説は統合 n 自信に応じて新たなマスクを作る

証拠固め

5. 判断 n n False Positive を減らすことを考える マスク内部が隠れるのは外部要因だけと 仮定 n n n つぼは見る角度で底が見えたり見えなかった りする→この場合は考慮しない 詳しいアルゴリズムは記述してない 単純に自信が大きいだけでなく、マスク全 体に自信があるものを採用するようだ

実験 n Graz-02 データセット n Aspect clusteringの効果 n 最新手法との比較(vs Shotton)

Graz-02 データセット画像の例
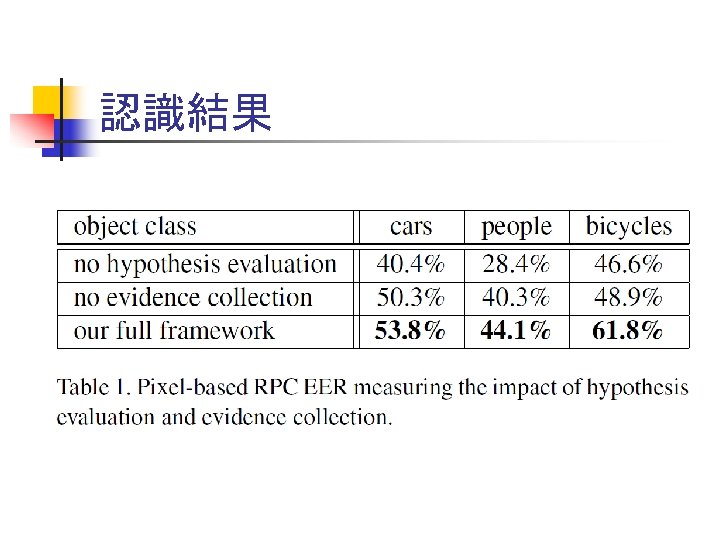
認識結果

輪郭抽出結果
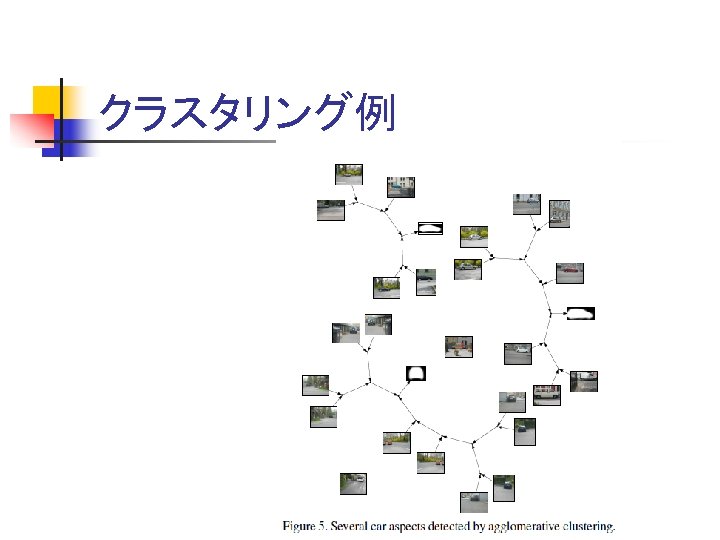
クラスタリング例
右側拡大
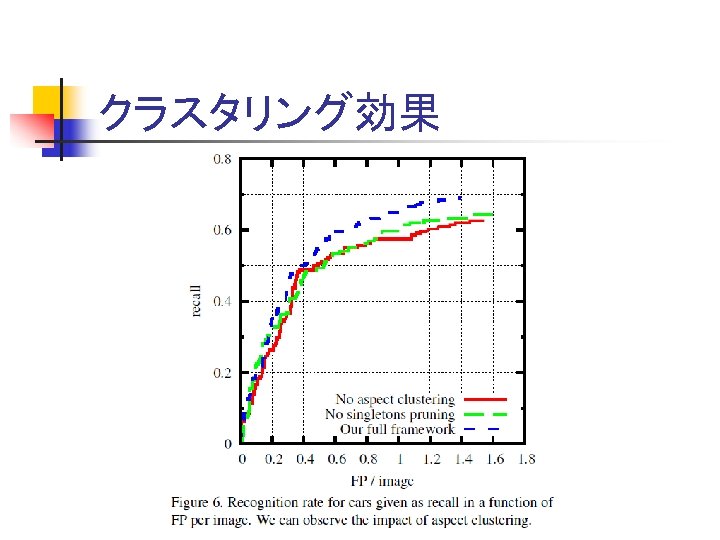
クラスタリング効果
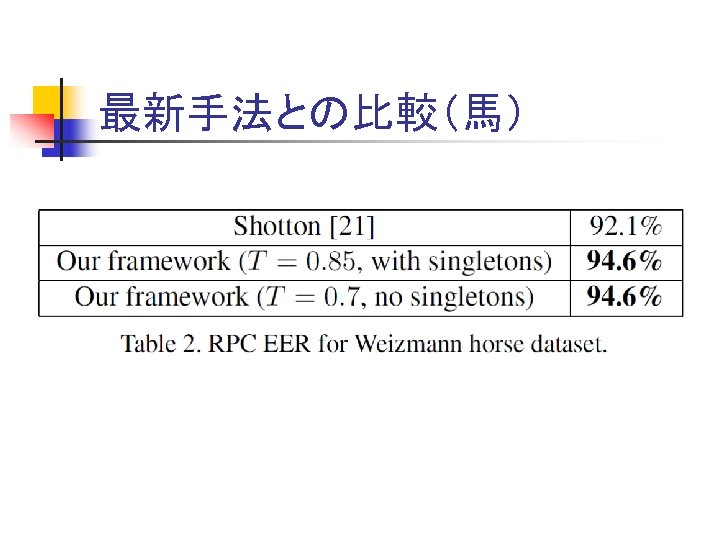
最新手法との比較(馬)

輪郭抽出結果(馬)

本論文のまとめ n n 輪郭マスクという大域的性質 特徴量の見えの位置という局所的性質 クラスマスクの生成 状態がよいデータセットでかなりよい結果

最後の論文 n n Deep Residual Learning for Image Recognition Kaiming He, Xiangyu Zhang, Shaoqing Ren, Jian Sun (Microsoft Research) CVPR 2016 Best Paper Award https: //arxiv. org/abs/1512. 03385

Vanishing Gradient Problem n Deep Learning は層が深い方が高精度 深くなると全体(共通)の特徴がでてくる ⇒最後の方は細かい差異が出にくい n filtering(+pooling) の繰り返し … 最後の方の調整は 最初の方にはあま り影響しない
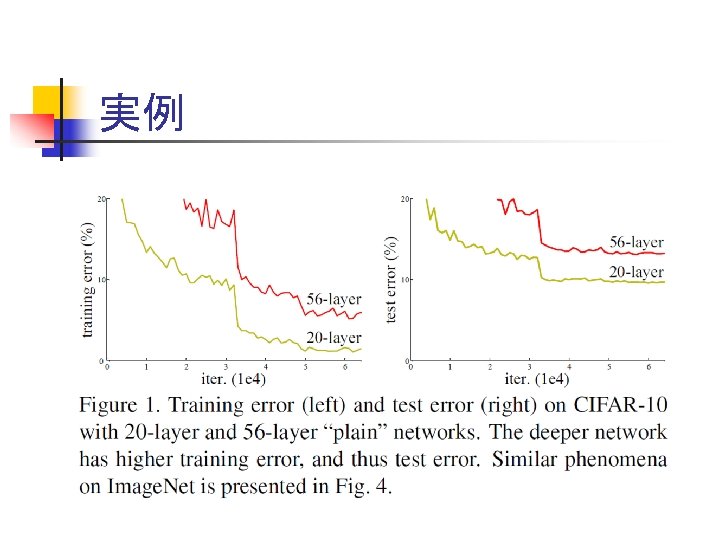
実例

恒等写像層 n n Layer を増やす単純な方法 Layer のコピーと恒等写像 n n L(i)=L(i+1) F: L(i)→L(i+1), F(x)=x L(i) L(i+1) F …

恒等写像層追加の影響 n 何もしないのと同じに思える n n よくなることはあっても悪くはならなさそう 実際にやってみると悪くなる n Vanishing Gradient Problem ではないか

「些細な」改良 n n 恒等写像との差(Residual) H を使う Layer のコピーとFと恒等写像の差Hを使う n n L(i)=L(i+1), F: L(i)→L(i+1) H: L(i)→L(i+1), H(x)=F(x)-x L(i) L(i+1) F L(i) L(i+1) H=F-I

Residual Learning(1) L(i)とL(i+k)のサイズが同じ時 F: L(i+k-1)→L(i+k) I_i: L(i)→L(i) (L(i)の恒等写像I_i(x)=x) n H: L(i+k-1)→L(i+k)を H(x)=F(x)-I_i(x) で定義する (F(x)=H(x)+I_i(x)でもある) n

Residual Learning(2) n L(i)とL(i+k)のサイズが違う時(u>d) L(i) n x m, depth d, (x 1, …, xd) n L(i+k) n/2 x m/2, depth u (x 1, …, xu) depthは埋め込み W W: L(i)→L(i+k), W(x)=(x 1, …, xd, 0, … 0) あるいは、W(xi)=a xi (1 x 1 フィルタ) n, mは同じように間引く n n H: L(i+k-1)→L(i+k)を H(x)=F(x)-W(x)
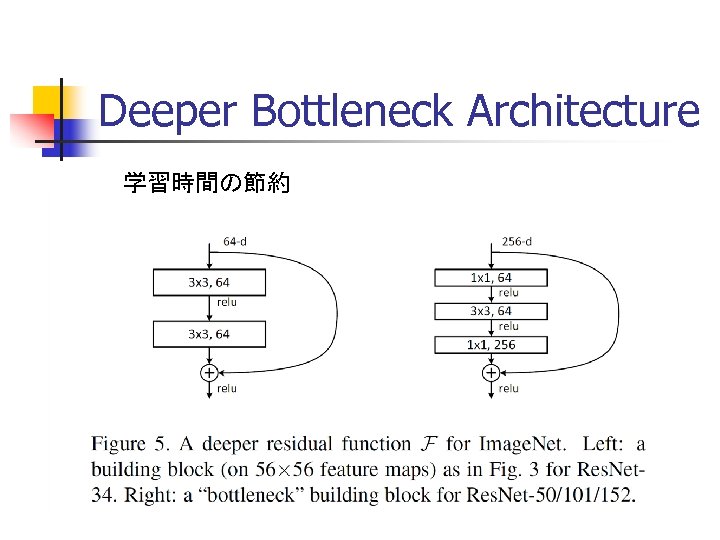
Deeper Bottleneck Architecture 学習時間の節約

Residual Learningを使うメリット n 以前のレイヤのデータが反映される n n n L(i)での差異がL(i+k)に影響する Vanishing Gradient Problem が抑えられる したがってレイヤを深くできる
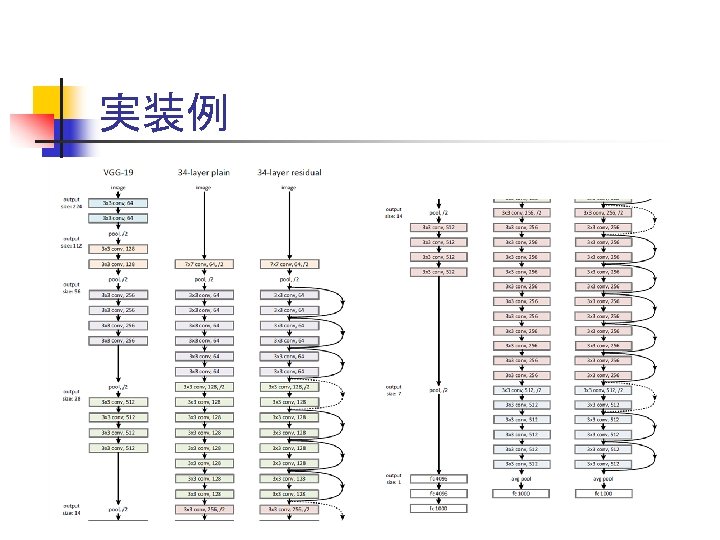
実装例
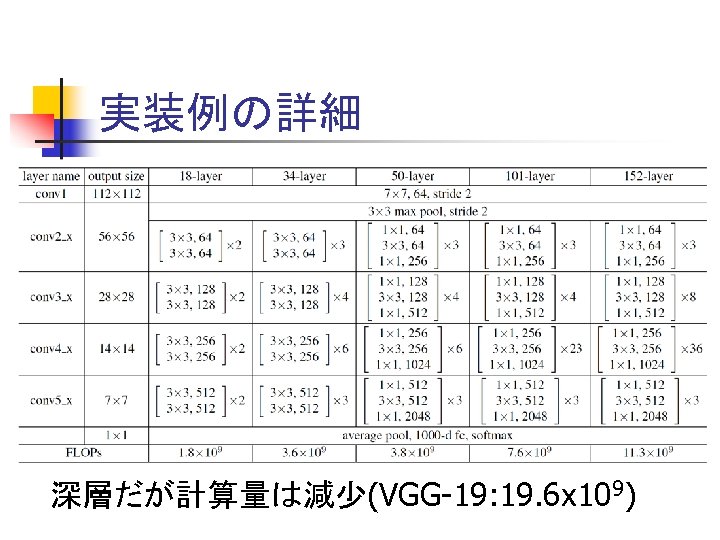
実装例の詳細 深層だが計算量は減少(VGG-19: 19. 6 x 109)
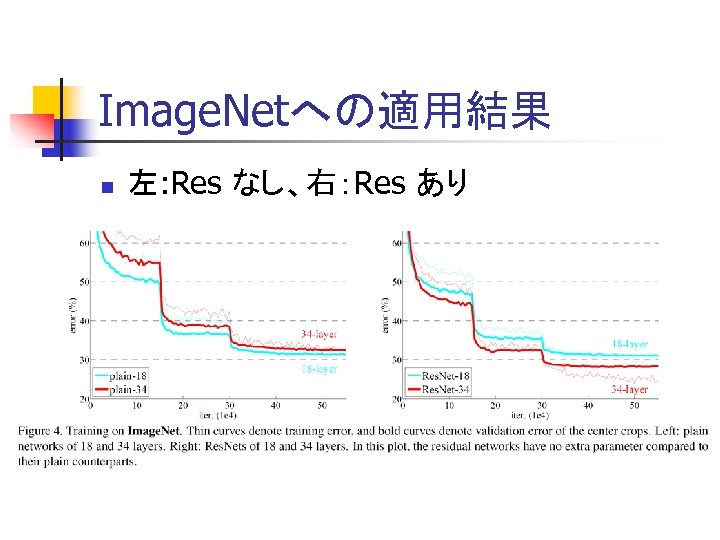
Image. Netへの適用結果 n 左: Res なし、右:Res あり

Image. Net での認識結果(1)
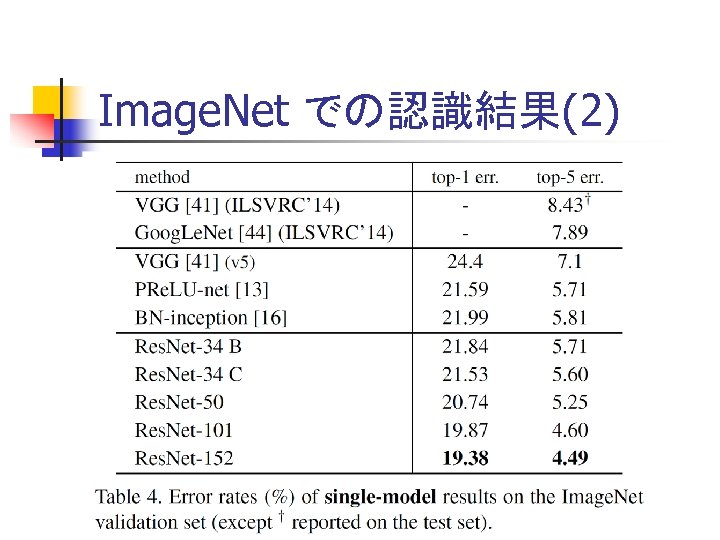
Image. Net での認識結果(2)

Image. Net での認識結果(3)
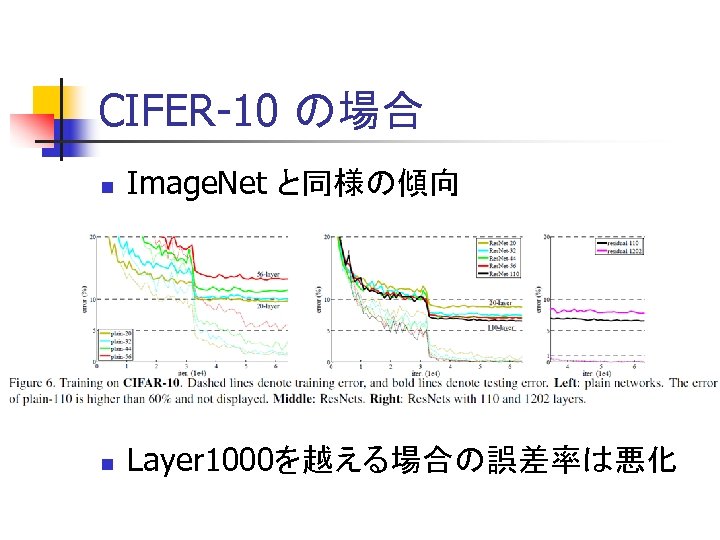
CIFER-10 の場合 n Image. Net と同様の傾向 n Layer 1000を越える場合の誤差率は悪化

CIFER-10 での認識結果

Deep Residual のまとめ n Layer増→高精度 とは限らない n 以前のと差分を評価すると可能になった n まだいくらでもLayerが増やせるわけではな い

まとめ n n 1枚の画像からのクラス認識手法3つ 局所的な特徴とその位置を利用 n n n 連続量で表現 事前学習で小さな次元のモデルを作る パッチベース→積分型 n 比較的安定

まとめ n 20 Qに例えて n n Deep. Learning n n n 多くの性質を同時に有するモノは少ない 0, 1 でなく連続量で性質を評価 どのような指標を用いどのように探索するか 力技で事前学習、力技で探索 理論(特徴量の意味)はないが結果はすごい 今後はDeep. Learning+理論的手法?
ef2f8f110c848463267d7aba16e30d1d.ppt