數位系統 Digital Systems Department of Computer Science and

數位系統 Digital Systems Department of Computer Science and Information Engineering, Chaoyang University of Technology 朝陽科技大學資 系 Speaker: Fuw-Yi Yang 楊伏夷 伏夷非征番, 道德經 察政章(Chapter 58) 伏 者潛藏也 道紀章(Chapter 14) 道無形象, 視之不可見者曰夷 Fuw-Yi Yang 1

Text Book: Digital Design 4 th Ed. Chap 5 Synchronous Sequential Logic 5. 1 Introduction 5. 2 Sequential Circuits 5. 3 Storage Elements: Latches 5. 4 Storage Elements: Flip-Flops 5. 5 Analysis of Clocked Sequential Circuits 5. 6 Synthesizable HDL Models of Sequential Circuits 5. 7 State Reduction and Assignment 5. 8 Design Procedure Fuw-Yi Yang 2

Text Book: Digital Design 4 th Ed. Chap 5. 1 Introduction Although every digital system is likely to have some combinational circuits, most systems encountered in practice also include storage elements, which require that the system be described in terms of sequential logic. First, we need to understand what distinguishes sequential logic from combinational logic. Fuw-Yi Yang 3

Text Book: Digital Design 4 th Ed. Chap 5. 2 sequential circuits A block diagram of a sequential circuit is shown above. Fuw-Yi Yang 4

Text Book: Digital Design 4 th Ed. Chap 5. 2 Sequential circuits There are two main types of sequential circuits, and their classification is a function of the timing of their signals. A synchronous sequential circuit is a system whose behavior can be defined from the knowledge of its signals at discrete instants of time. The behavior of an asynchronous sequential circuit depends upon the input signals at any instant of time and the order in which the inputs change. Fuw-Yi Yang 5

Text Book: Digital Design 4 th Ed. Chap 5. 2 Sequential circuits A synchronous sequential circuit employs signals that affect the storage elements at only discrete instants of time. Synchronization is achieved by a time device called a clock generator, which provides a clock signal having the form of a period train of clock pulses. Synchronous sequential circuits that use clock pulses to control storage elements are called clocked sequential circuits and are the type most frequently encountered in practice. (next page) Fuw-Yi Yang 6

Text Book: Digital Design 4 th Ed. Chap 5. 2 Sequential Circuits – Synchronous Clocked Sequential Circuit Fuw-Yi Yang 7

Text Book: Digital Design 4 th Ed. Chap 5. 3 Storage Elements: Latches A storage element in a digital circuit can maintain a binary state indefinitely, until directed by an input signal to switch state. Storage elements that operate with signal levels are referred to as latches; those controlled by a clock transition are flip-flops. Latches are said to be level sensitive devices; flip-flops are edge-sensitive devices. Fuw-Yi Yang 8

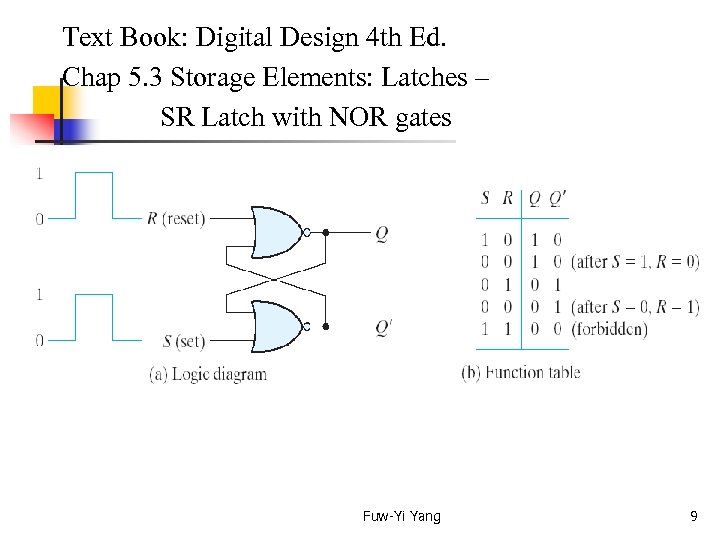
Text Book: Digital Design 4 th Ed. Chap 5. 3 Storage Elements: Latches – SR Latch with NOR gates Fuw-Yi Yang 9

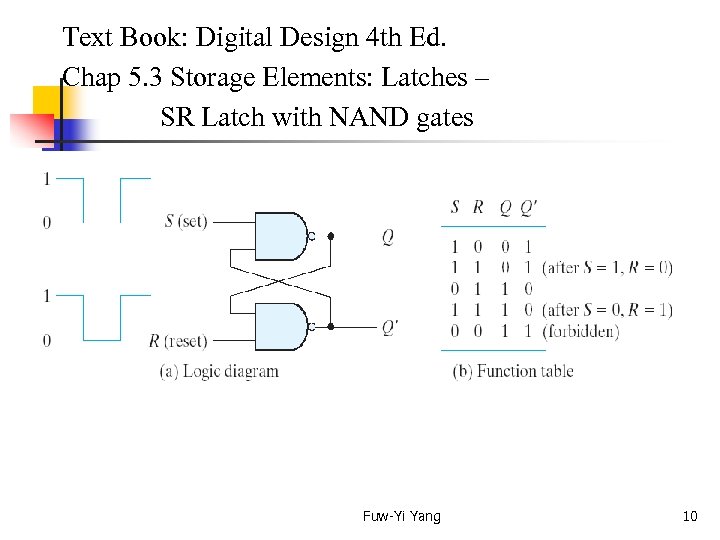
Text Book: Digital Design 4 th Ed. Chap 5. 3 Storage Elements: Latches – SR Latch with NAND gates Fuw-Yi Yang 10

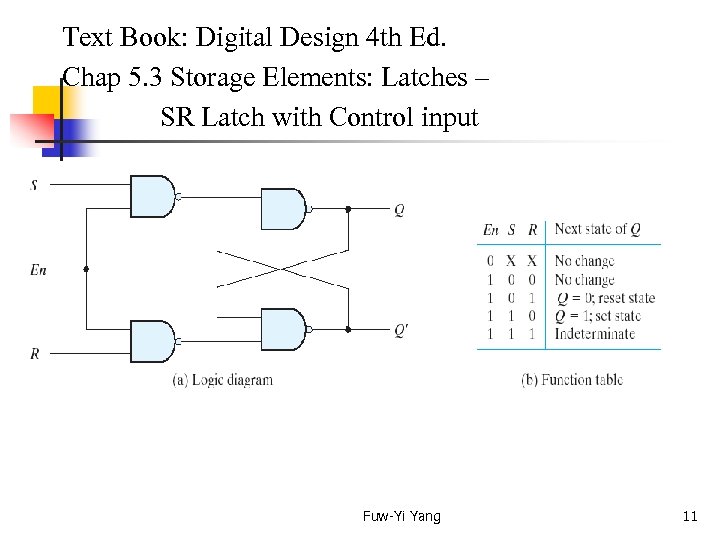
Text Book: Digital Design 4 th Ed. Chap 5. 3 Storage Elements: Latches – SR Latch with Control input Fuw-Yi Yang 11

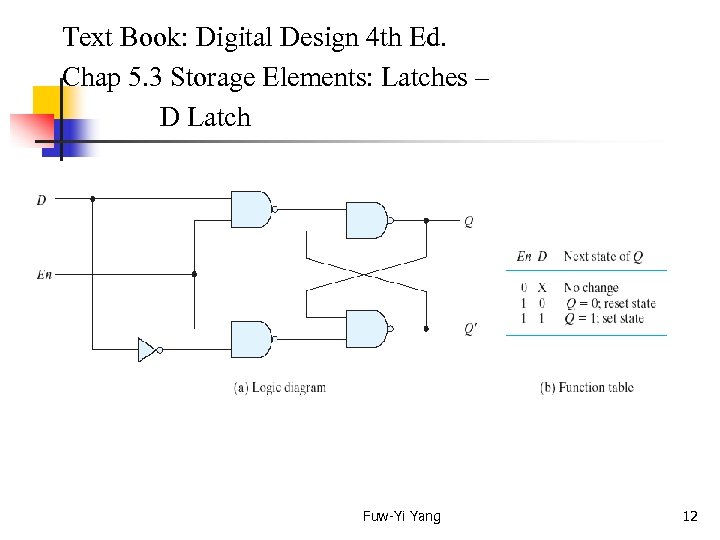
Text Book: Digital Design 4 th Ed. Chap 5. 3 Storage Elements: Latches – D Latch Fuw-Yi Yang 12

Text Book: Digital Design 4 th Ed. Chap 5. 3 Storage Elements: Latches – Graphic symbols for latches Fuw-Yi Yang 13

Text Book: Digital Design 4 th Ed. Chap 5. 4 Storage Elements: Flip-Flops The state of a latch or flip-flop is switched by a change in the control input. This momentary change is called a trigger, and the transition it causes is said to trigger the flip-flop. Fuw-Yi Yang 14

Text Book: Digital Design 4 th Ed. Chap 5. 4 Storage Elements: Flip-Flops Responses---level signal or edged signal Fuw-Yi Yang 15

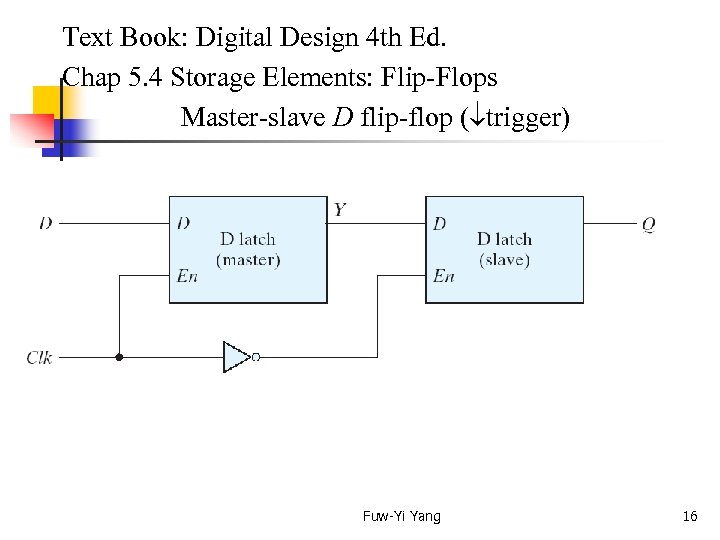
Text Book: Digital Design 4 th Ed. Chap 5. 4 Storage Elements: Flip-Flops Master-slave D flip-flop ( trigger) Fuw-Yi Yang 16

Text Book: Digital Design 4 th Ed. Chap 5. 4 Storage Elements: Flip-Flops D-type positive-edge-triggered flip-flop Fuw-Yi Yang 17

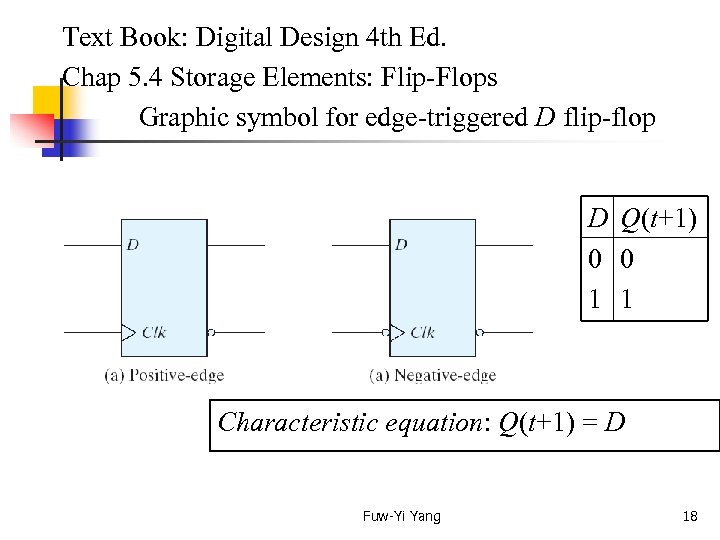
Text Book: Digital Design 4 th Ed. Chap 5. 4 Storage Elements: Flip-Flops Graphic symbol for edge-triggered D flip-flop D Q(t+1) 0 0 1 1 Characteristic equation: Q(t+1) = D Fuw-Yi Yang 18

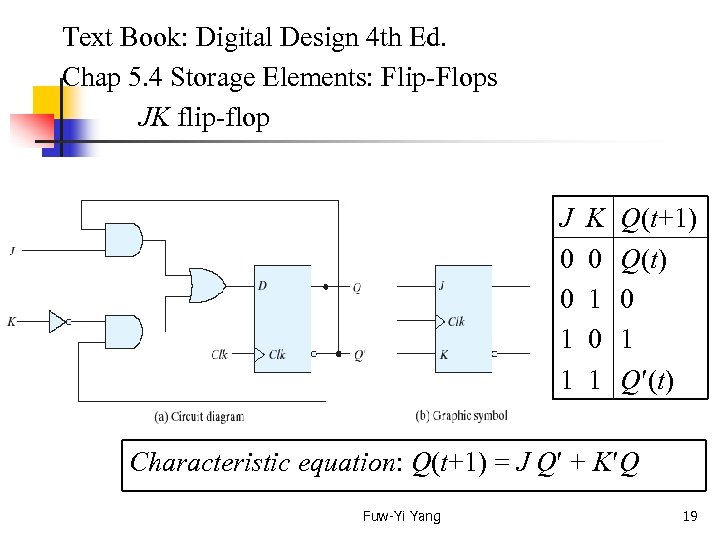
Text Book: Digital Design 4 th Ed. Chap 5. 4 Storage Elements: Flip-Flops JK flip-flop J K 0 0 0 1 1 Q(t+1) Q(t) 0 1 Q (t) Characteristic equation: Q(t+1) = J Q + K Q Fuw-Yi Yang 19

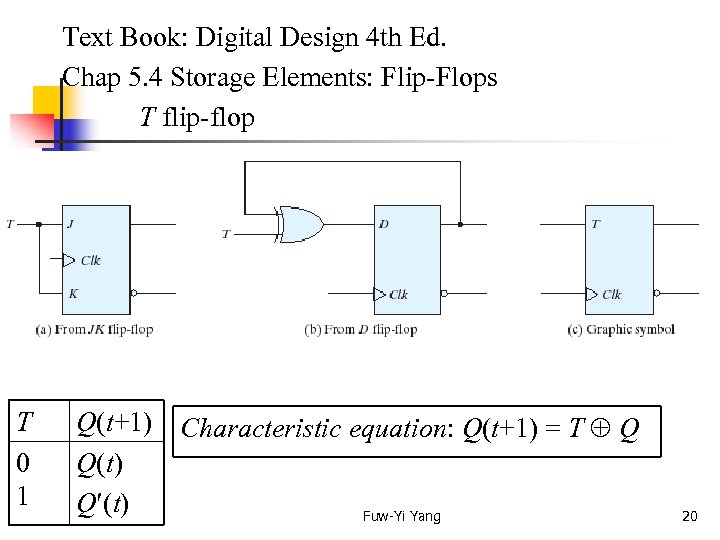
Text Book: Digital Design 4 th Ed. Chap 5. 4 Storage Elements: Flip-Flops T flip-flop T Q(t+1) Characteristic equation: Q(t+1) = T Q 0 Q(t) 1 Q (t) Fuw-Yi Yang 20

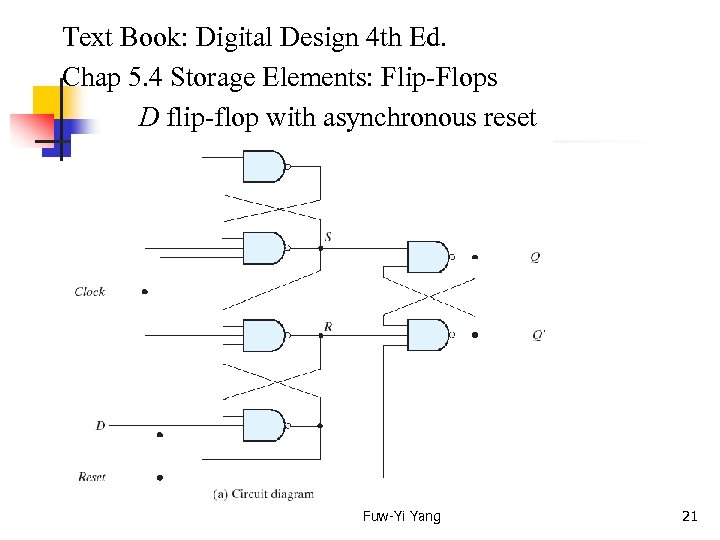
Text Book: Digital Design 4 th Ed. Chap 5. 4 Storage Elements: Flip-Flops D flip-flop with asynchronous reset Fuw-Yi Yang 21

Text Book: Digital Design 4 th Ed. Chap 5. 4 Storage Elements: Flip-Flops D flip-flop with asynchronous reset R Clk D 0 X X 1 0 1 1 Q 0 0 1 Fuw-Yi Yang 22

Text Book: Digital Design 4 th Ed. Chap 5. 5 Analysis of Clocked Sequential Circuits State equation The behavior of a clocked sequential circuit can be described by means of state equation. A state equation (also called transition equation) specifies the next state as a function of the present state and inputs. For example, the characteristic equations of T flip-flop, D flip-flop, and JK flip-flop specifies their next states as: Q(t+1) = T Q, Q(t+1) = D, and Q(t+1) = J Q + K Q, respectively. An example of sequential circuit is analyzed in next page. Fuw-Yi Yang 23

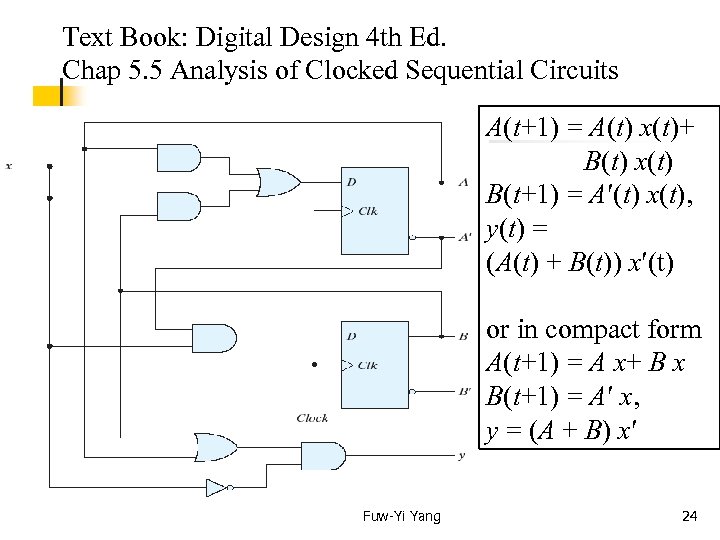
Text Book: Digital Design 4 th Ed. Chap 5. 5 Analysis of Clocked Sequential Circuits A(t+1) = A(t) x(t)+ B(t) x(t) B(t+1) = A (t) x(t), y(t) = (A(t) + B(t)) x (t) or in compact form A(t+1) = A x+ B x B(t+1) = A x, y = (A + B) x Fuw-Yi Yang 24

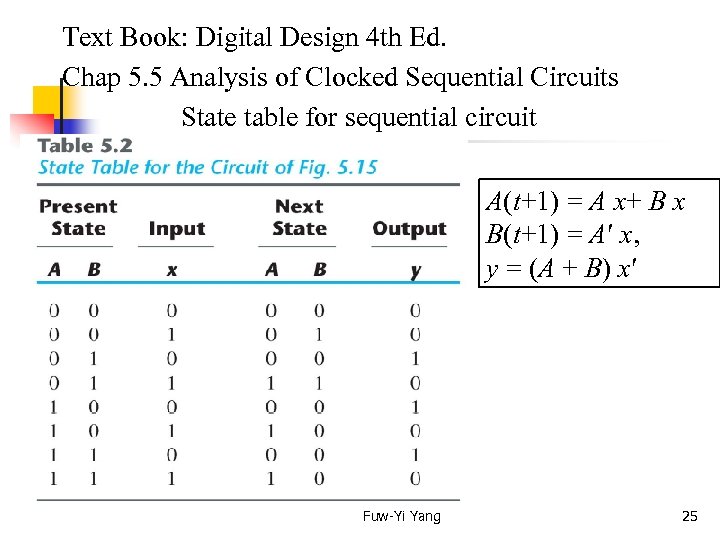
Text Book: Digital Design 4 th Ed. Chap 5. 5 Analysis of Clocked Sequential Circuits State table for sequential circuit A(t+1) = A x+ B x B(t+1) = A x, y = (A + B) x Fuw-Yi Yang 25

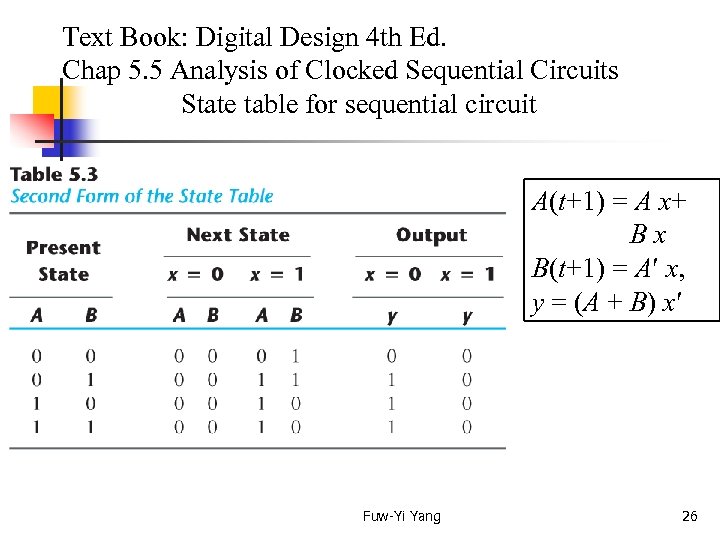
Text Book: Digital Design 4 th Ed. Chap 5. 5 Analysis of Clocked Sequential Circuits State table for sequential circuit A(t+1) = A x+ B x B(t+1) = A x, y = (A + B) x Fuw-Yi Yang 26

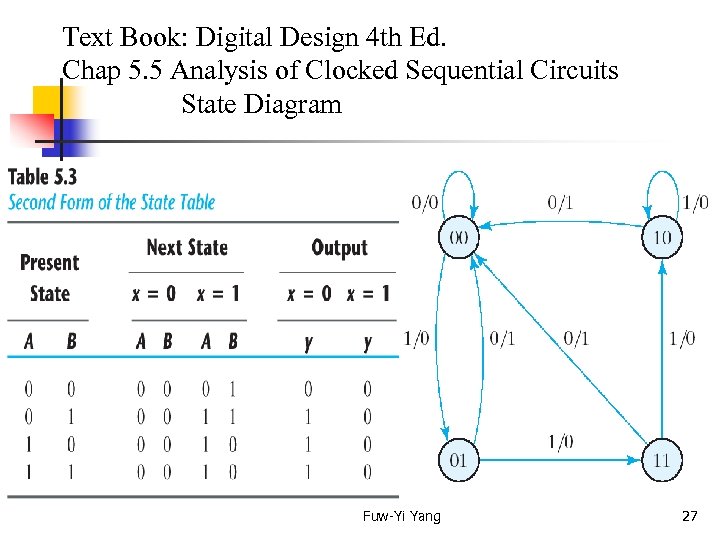
Text Book: Digital Design 4 th Ed. Chap 5. 5 Analysis of Clocked Sequential Circuits State Diagram Fuw-Yi Yang 27

Text Book: Digital Design 4 th Ed. Chap 5. 5 Analysis of Clocked Sequential Circuits Flip-Flop input equations The logic diagram of a sequential circuit consists of flip-flops and gates. The interconnections among the gates form a combinational circuit and may be specified algebraically with Boolean expressions. The knowledge of the type of flip-flops and a list of the Boolean expressions of the combinational circuit provide the information needed to draw the logic diagram of the sequential circuit. Fuw-Yi Yang 28

Text Book: Digital Design 4 th Ed. Chap 5. 5 Analysis of Clocked Sequential Circuits Flip-Flop input equations The part of the combinational circuit that generates external outputs is described algebraically by a set of Boolean functions called output equations. The part of the circuit that generates the inputs of flip-flops is described algebraically by a set of Boolean functions called flip-flop input equations (or excitation equations). For the circuit in Fig 5 -15, we have (next page) Input equations: DA = A x+ B x, DB = A x, Output equations: y = (A + B) x Fuw-Yi Yang 29

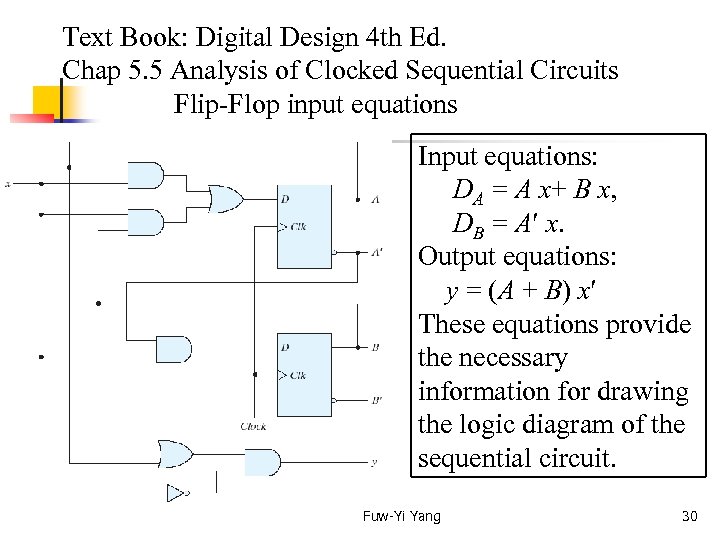
Text Book: Digital Design 4 th Ed. Chap 5. 5 Analysis of Clocked Sequential Circuits Flip-Flop input equations Input equations: DA = A x+ B x, DB = A x. Output equations: y = (A + B) x These equations provide the necessary information for drawing the logic diagram of the sequential circuit. Fuw-Yi Yang 30

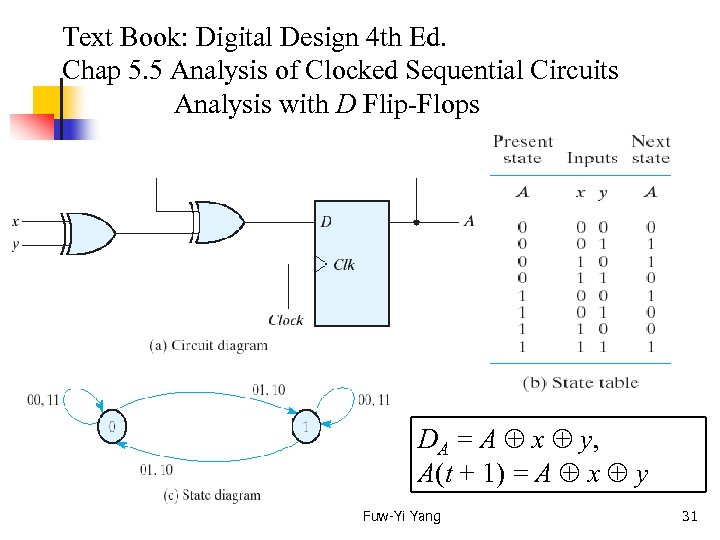
Text Book: Digital Design 4 th Ed. Chap 5. 5 Analysis of Clocked Sequential Circuits Analysis with D Flip-Flops DA = A x y, A(t + 1) = A x y Fuw-Yi Yang 31

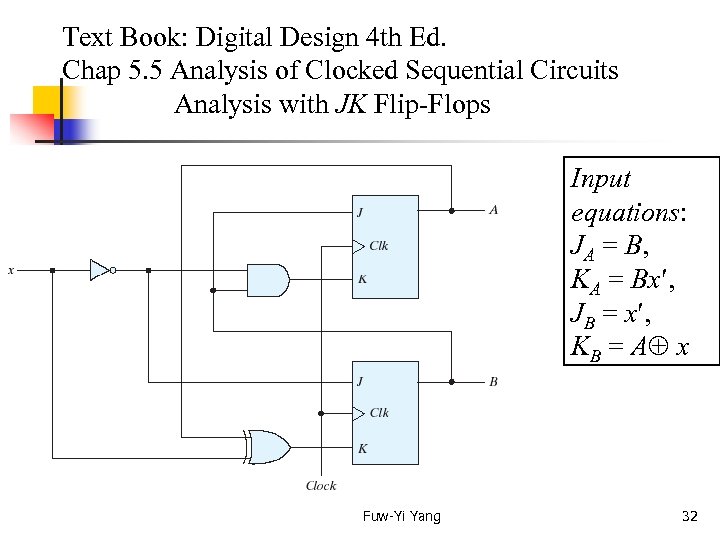
Text Book: Digital Design 4 th Ed. Chap 5. 5 Analysis of Clocked Sequential Circuits Analysis with JK Flip-Flops Input equations: JA = B, KA = Bx , JB = x , KB = A x Fuw-Yi Yang 32

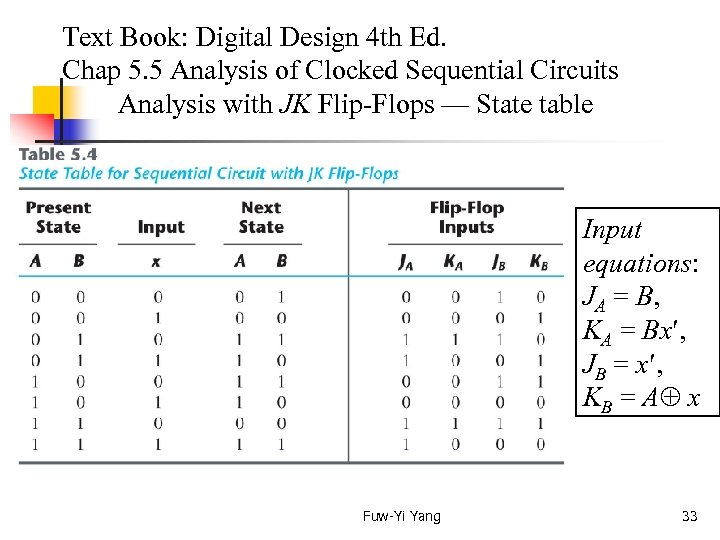
Text Book: Digital Design 4 th Ed. Chap 5. 5 Analysis of Clocked Sequential Circuits Analysis with JK Flip-Flops — State table Input equations: JA = B, KA = Bx , JB = x , KB = A x Fuw-Yi Yang 33

Text Book: Digital Design 4 th Ed. Chap 5. 5 Analysis of Clocked Sequential Circuits Analysis with JK Flip-Flops—State equations Input equations: JA = B, KA = Bx , JB = x , KB = A x Characteristic equation: Q(t+1) = J Q + K Q A(t+1) = JAA + KA A = BA + (Bx ) A = BA + B A + x. A B(t+1) = JBB + KB B = x B + (A x) B = x B + ABx+ A Bx Fuw-Yi Yang 34

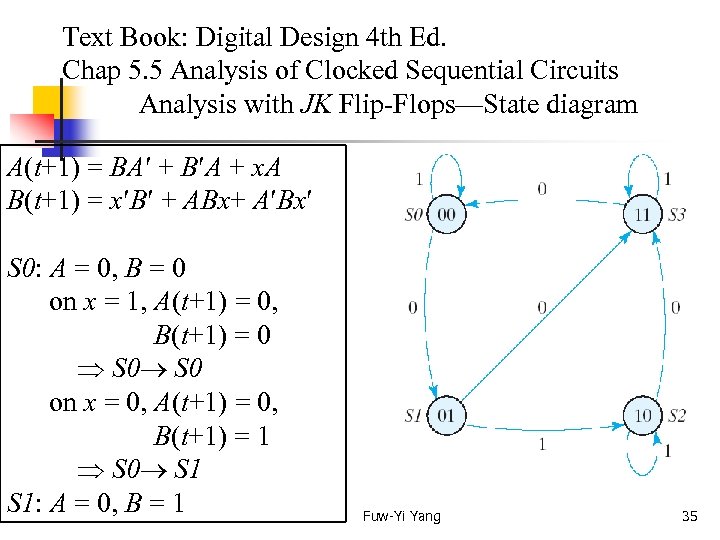
Text Book: Digital Design 4 th Ed. Chap 5. 5 Analysis of Clocked Sequential Circuits Analysis with JK Flip-Flops—State diagram A(t+1) = BA + B A + x. A B(t+1) = x B + ABx+ A Bx S 0: A = 0, B = 0 on x = 1, A(t+1) = 0, B(t+1) = 0 S 0 on x = 0, A(t+1) = 0, B(t+1) = 1 S 0 S 1: A = 0, B = 1 Fuw-Yi Yang 35

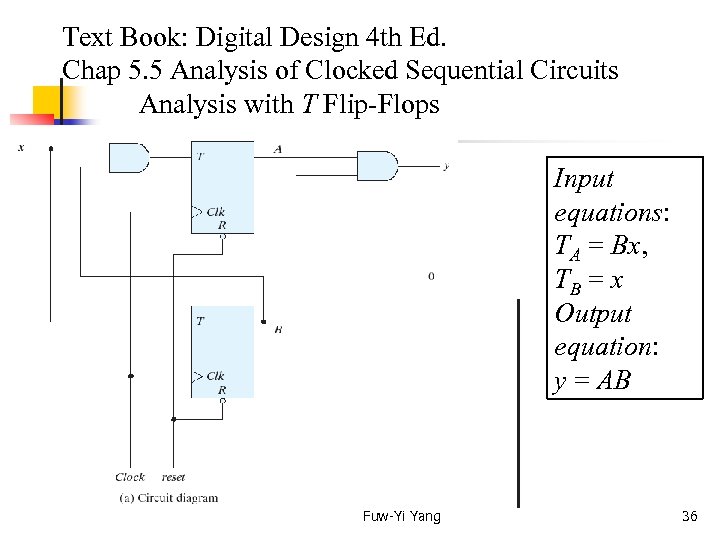
Text Book: Digital Design 4 th Ed. Chap 5. 5 Analysis of Clocked Sequential Circuits Analysis with T Flip-Flops Input equations: TA = Bx, TB = x Output equation: y = AB Fuw-Yi Yang 36

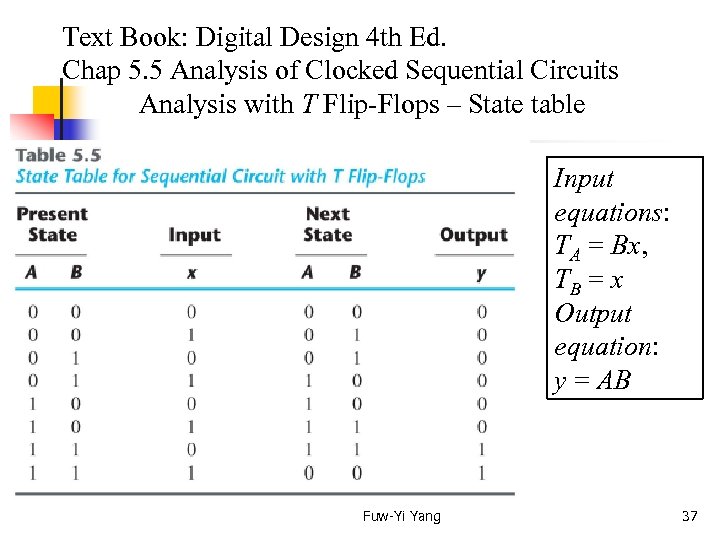
Text Book: Digital Design 4 th Ed. Chap 5. 5 Analysis of Clocked Sequential Circuits Analysis with T Flip-Flops – State table Input equations: TA = Bx, TB = x Output equation: y = AB Fuw-Yi Yang 37

Text Book: Digital Design 4 th Ed. Chap 5. 5 Analysis of Clocked Sequential Circuits Analysis with T Flip-Flops – State equations Input equations: TA = Bx, TB = x Output equation: y = AB Characteristic equation: Q(t+1) = T Q A(t+1) = (TA A) = (Bx A) = (Bx) A + (Bx)A = AB + Ax + A Bx B(t+1) = (TB B) = (x B) Fuw-Yi Yang 38

Text Book: Digital Design 4 th Ed. Chap 5. 5 Analysis of Clocked Sequential Circuits Analysis with T Flip-Flops – State diagram A(t+1) = (Bx A) B(t+1) = (x B) y = AB 00/0: A = 0, B = 0, y = 0 on x = 1: A(t+1) = 0, B(t+1) = 1, y = 0 00/0 01/0 on x = 0: A(t+1) = 0, B(t+1) = 0, y = 0 00/0 Fuw-Yi Yang 39

Text Book: Digital Design 4 th Ed. Chap 5. 5 Analysis of Clocked Sequential Circuits Mealy and Moore Models of Finite State Machine The most general model of a sequential circuit has inputs, outputs, and internal states. It is customary to distinguish between two models of sequential circuits: the Mealy model and the Moore model. They differ only in the way the outputs is generated. In the Mealy model, the output is a function of both the present state and the input. In the Moore model, the output is a function of only the present state. See next page Fuw-Yi Yang 40

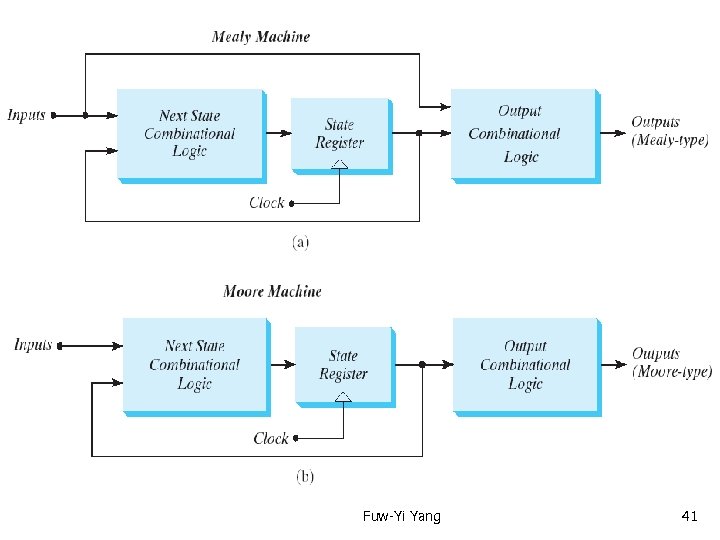
Text Book: Digital Design 4 th Ed. Chap 5. 5 Analysis of Clocked Sequential Circuits Mealy and Moore Models of Finite State Machine Fuw-Yi Yang 41

Text Book: Digital Design 4 th Ed. Chap 5. 6 Synthesizable HDL Models of Sequential Circuits // Description of D flip-flop // See Fig. 5 -11 module D_flip_flop (Q, D, CLK); output Q; input D, CLK; reg Q; always @ (posedge CLK) Q <= D; Endmodule Fuw-Yi Yang 42

Text Book: Digital Design 4 th Ed. Chap 5. 7 State Reduction and Assignment The analysis of sequential circuits starts from a circuit diagram and culminates in a state table or diagram. The design (synthesis) of a sequential circuit starts from a set of specifications and culminates in a logic diagram. Fuw-Yi Yang 43

Text Book: Digital Design 4 th Ed. Chap 5. 7 State Reduction and Assignment Two sequential circuits may exhibit the same input-output behavior, but have a different number of internal states (flip-flops) in their state diagram. Reducing the number of internal states may simplify a design. The reduction in the number of flip-flops in a sequential circuit is referred to as state-reduction problem. Fuw-Yi Yang 44

Example State a a b c d e f f g… Fuw-Yi Yang input 0 1 0 1 1 0 0… output 0 0 0 1 1 0 0 … 45

Text Book: Digital Design 4 th Ed. Chap 5. 7 State Reduction and Assignment – example -- state reduction If identical input sequences are applied to the two circuits and identical outputs occur for all input sequences, then the two circuits are said to be equivalent (as far as the input-out is concerned) and one may be replaced by the other. The problem of state reduction is to find ways of reducing the number of states in a sequential circuit without altering the input-output relationship. Fuw-Yi Yang 46

Text Book: Digital Design 4 th Ed. Chap 5. 7 State Reduction and Assignment – example -- state reduction The following algorithm for the state reduction of a completely specified state table is given without proof: Two states are said to be equivalent if for each member of the set of inputs, they give exactly the same output and send the circuit either to the same state or to an equivalent state. When two states are equivalent one of them can be removed without altering the input-output relationship. Fuw-Yi Yang 47

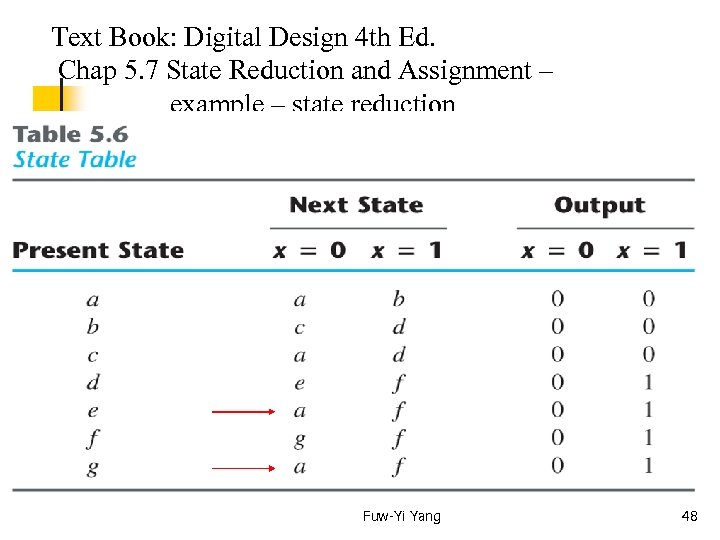
Text Book: Digital Design 4 th Ed. Chap 5. 7 State Reduction and Assignment – example – state reduction Fuw-Yi Yang 48

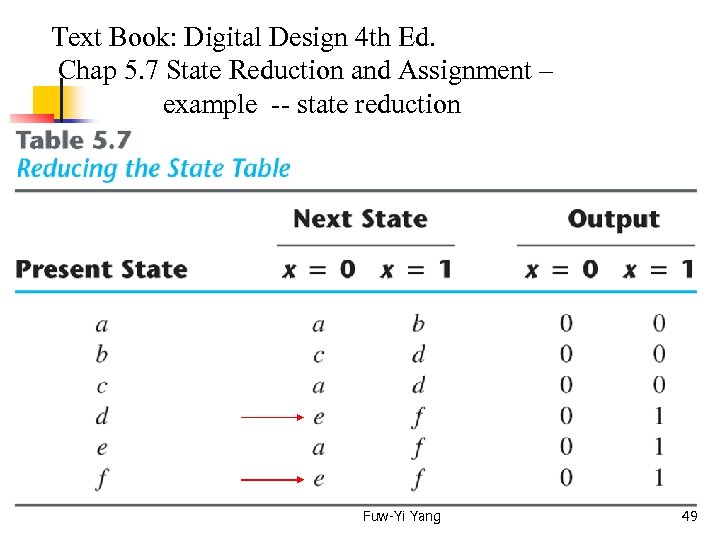
Text Book: Digital Design 4 th Ed. Chap 5. 7 State Reduction and Assignment – example -- state reduction Fuw-Yi Yang 49

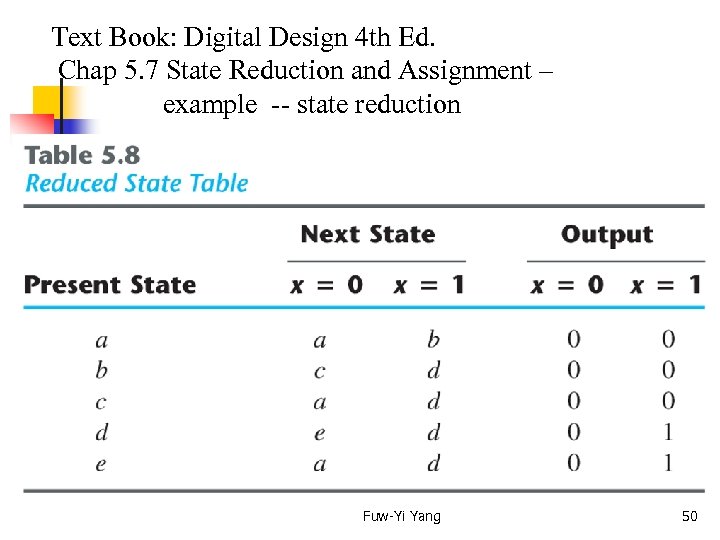
Text Book: Digital Design 4 th Ed. Chap 5. 7 State Reduction and Assignment – example -- state reduction Fuw-Yi Yang 50

Example – final result Reduced state diagram Fuw-Yi Yang 51

Text Book: Digital Design 4 th Ed. Chap 5. 7 State Reduction and Assignment -- example – state assignment In order to design a sequential circuit with physical components, it is necessary to assign unique coded binary values to the states. For a circuit with m states, the codes must contains n bits, where m 2 n. (next page shows examples of assignment) Unused states are treated as don’t care conditions during the design. Sometimes, the name transition table is used for a state table with a binary assignment. This convention distinguishes it from a state table with symbolic names for the states. Fuw-Yi Yang 52

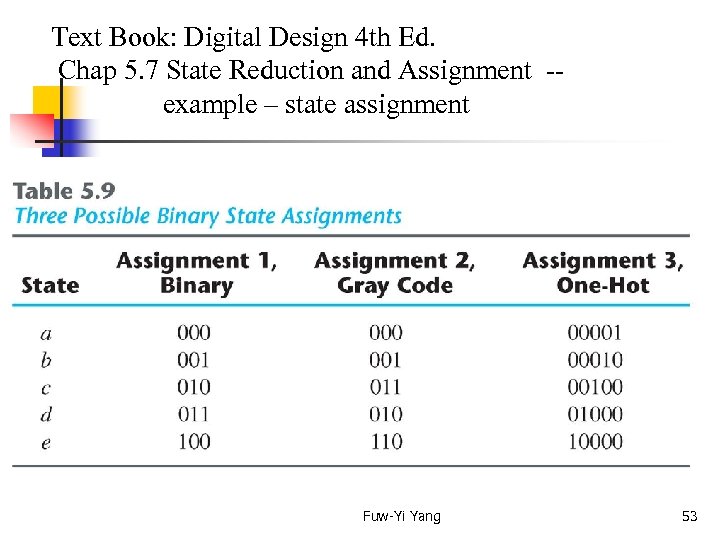
Text Book: Digital Design 4 th Ed. Chap 5. 7 State Reduction and Assignment -- example – state assignment Fuw-Yi Yang 53

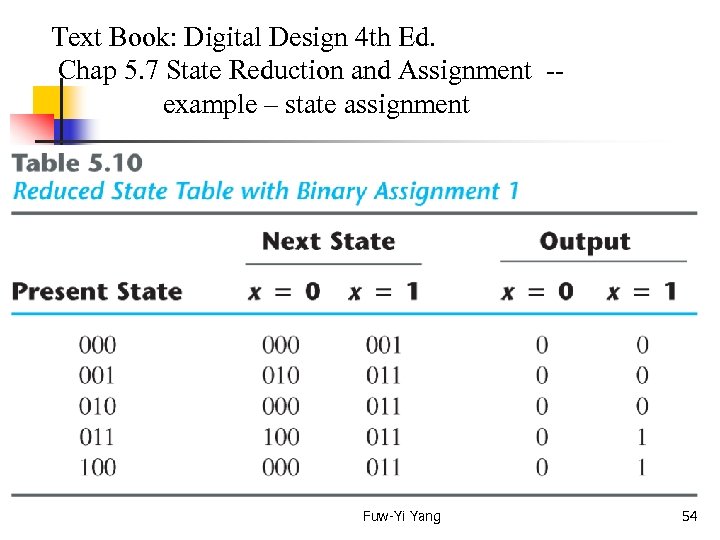
Text Book: Digital Design 4 th Ed. Chap 5. 7 State Reduction and Assignment -- example – state assignment Fuw-Yi Yang 54

Text Book: Digital Design 4 th Ed. Chap 5. 8 Design procedures or methodologies specify hardware that will implement a desired behavior. The design effort for small circuits may be manual, but industry relies on automated synthesis tools for designing massive integrated circuits. The building block used by synthesis tools is the D flipflop. Together with additional logic, it can implement the behavior of JK and T flip-flop. Fuw-Yi Yang 55

Text Book: Digital Design 4 th Ed. Chap 5. 8 Design procedure The procedure for designing synchronous sequential circuits can be summarized by a list of recommended steps: 1. From specification of the desired operation, derive a state diagram for the circuit. 2. Reduce the number of states if necessary. 3. Assign binary values to the states. 4. Obtain the binary-coded state table (transition table). 5. Choose the type of flip-flops to be used. 6. Derive the simplified flip-flop input equations and output equations. 7 Draw the logic diagram. Fuw-Yi Yang 56

Text Book: Digital Design 4 th Ed. Chap 5. 8 Design procedure -- example Specification: Suppose we wish to design a circuit that detects a sequence of three or more consecutive 1’s in a string of bits coming through an input line. Fuw-Yi Yang 57

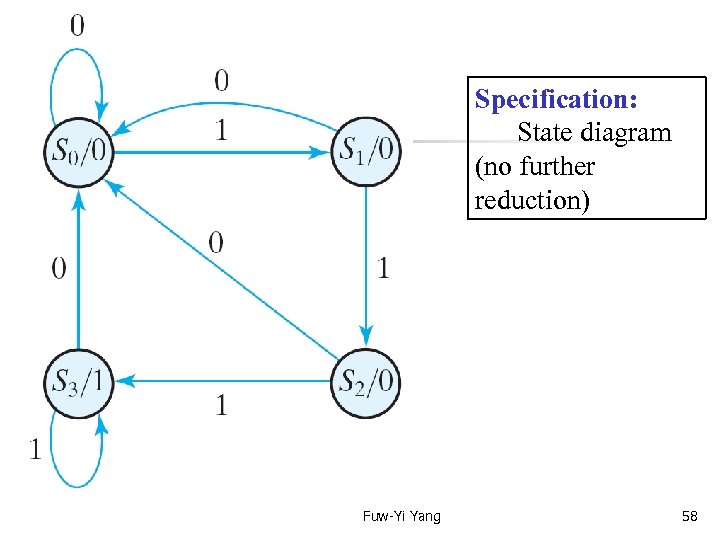
Specification: State diagram (no further reduction) Fuw-Yi Yang 58

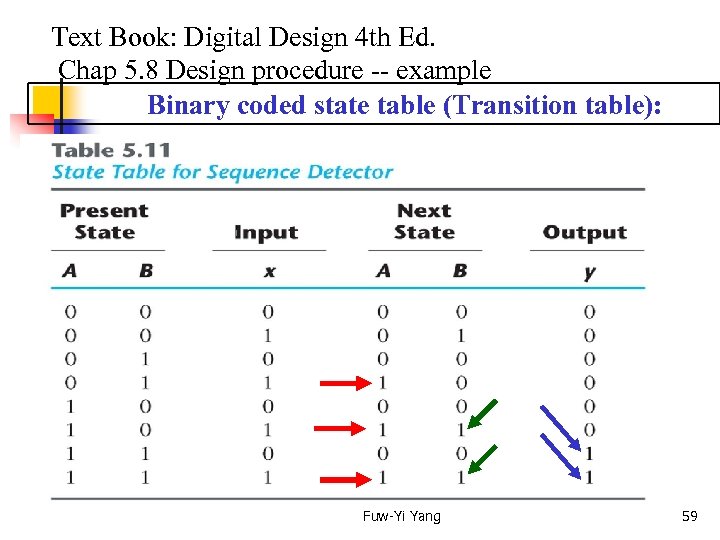
Text Book: Digital Design 4 th Ed. Chap 5. 8 Design procedure -- example Binary coded state table (Transition table): Fuw-Yi Yang 59

Text Book: Digital Design 4 th Ed. Chap 5. 8 Design procedure -- example Synthesis using D flip-flops: the characteristic equations of T flip-flop, D flip-flop, and JK flip-flop specifies their next states as: Q(t+1) = T Q, Q(t+1) = D, and Q(t+1) = J Q + K Q, respectively. From Transition table: A(t + 1) = DA(A, B, x) = (3, 5, 7) B(t + 1) = DB(A, B, x) = (1, 5, 7) y(A, B, x) = (6, 7) Fuw-Yi Yang 60

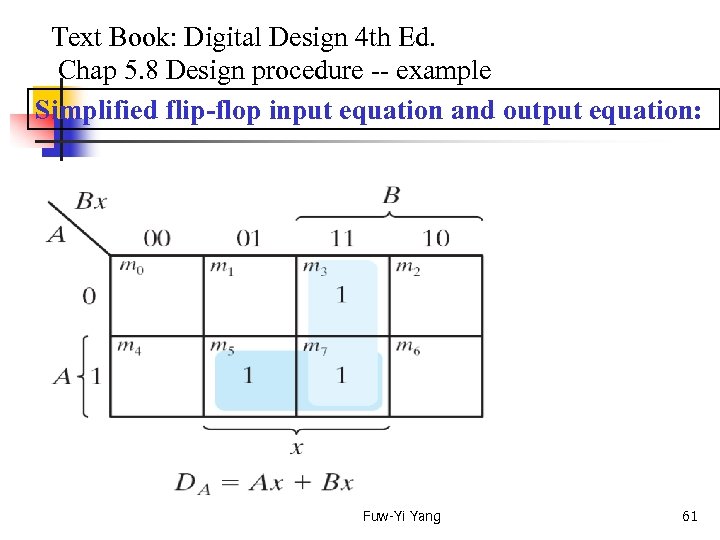
Text Book: Digital Design 4 th Ed. Chap 5. 8 Design procedure -- example Simplified flip-flop input equation and output equation: Fuw-Yi Yang 61

Text Book: Digital Design 4 th Ed. Chap 5. 8 Design procedure -- example Simplified flip-flop input equation and output equation: Fuw-Yi Yang 62

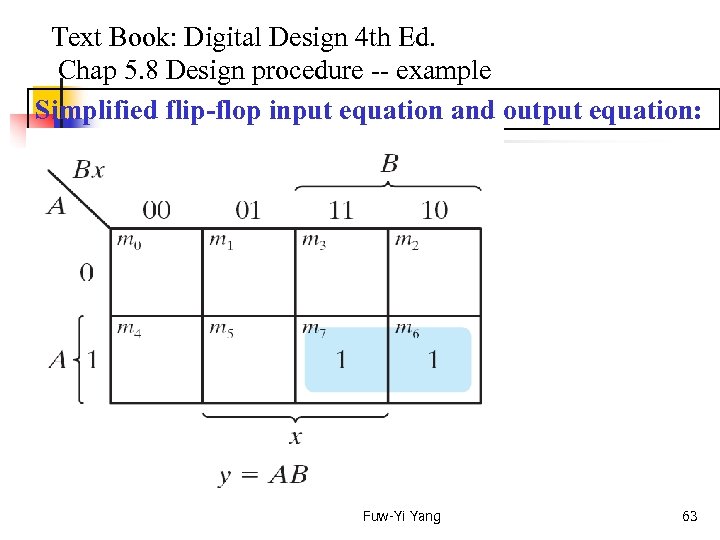
Text Book: Digital Design 4 th Ed. Chap 5. 8 Design procedure -- example Simplified flip-flop input equation and output equation: Fuw-Yi Yang 63

Logic Diagram: Fuw-Yi Yang 64

Text Book: Digital Design 4 th Ed. Chap 5. 8 Design procedure – excitation tables The design of a sequential circuit with flip-flops other than the D type flip-flop is complicated by the fact that the input equations for the circuit must be derived indirectly from the state table. When D type flip-flop are employed, the input equations are obtained directly from the state table. This is not the case for the JK and T types of flip-flops (refer to the characteristic equations Q(t+1) = T Q, Q(t+1) = D, and Q(t+1) = J Q + K Q, ). Fuw-Yi Yang 65

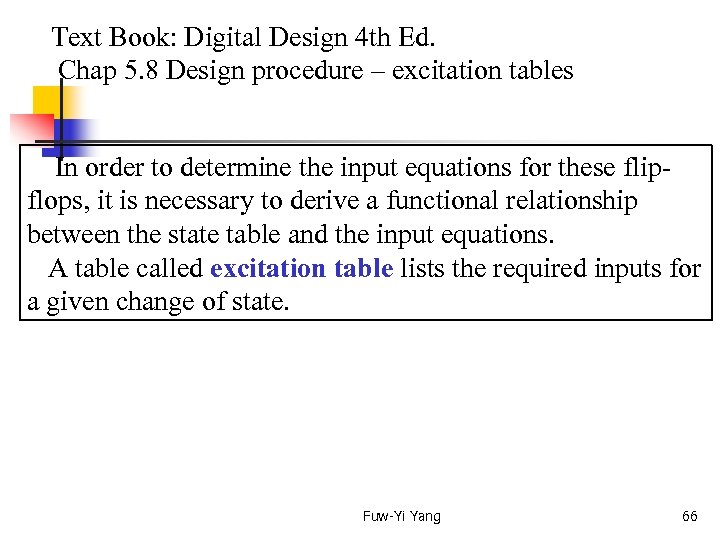
Text Book: Digital Design 4 th Ed. Chap 5. 8 Design procedure – excitation tables In order to determine the input equations for these flipflops, it is necessary to derive a functional relationship between the state table and the input equations. A table called excitation table lists the required inputs for a given change of state. Fuw-Yi Yang 66

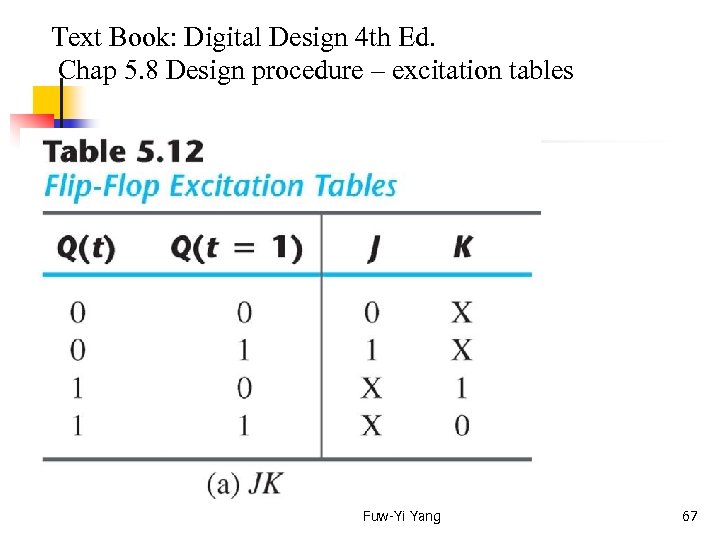
Text Book: Digital Design 4 th Ed. Chap 5. 8 Design procedure – excitation tables Fuw-Yi Yang 67

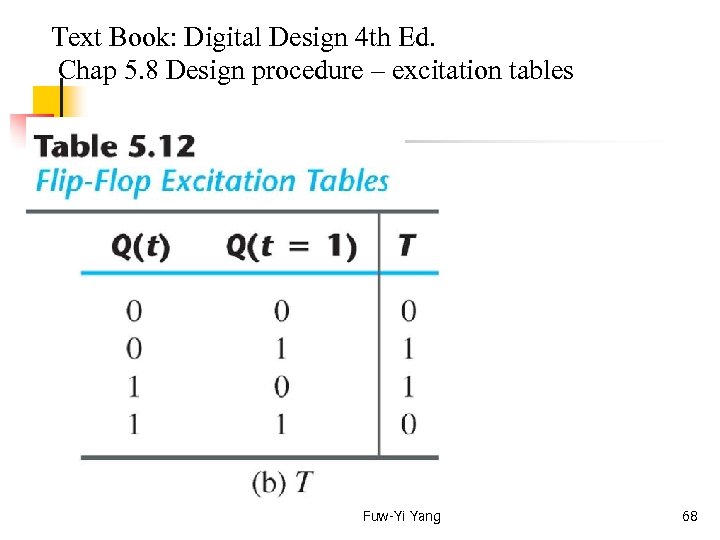
Text Book: Digital Design 4 th Ed. Chap 5. 8 Design procedure – excitation tables Fuw-Yi Yang 68

Text Book: Digital Design 4 th Ed. Chap 5. 8 Design procedure -- example Synthesis using JK flip-flops: Fuw-Yi Yang 69

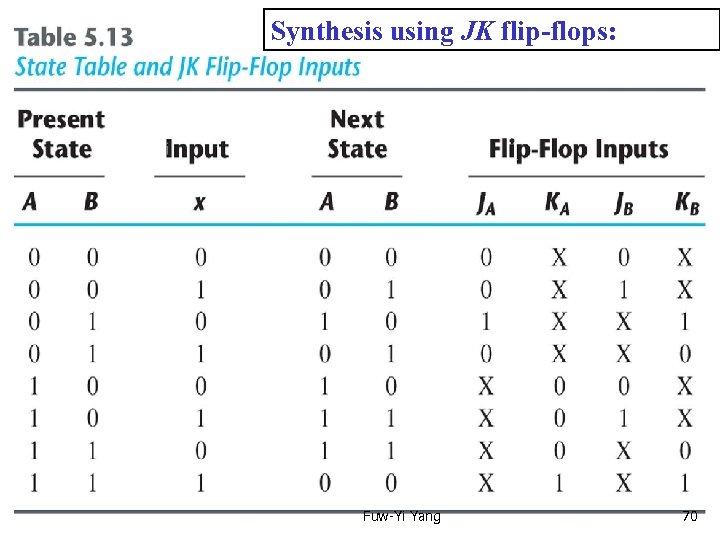
Synthesis using Text Book: Digital Design 4 th Ed. JK flip-flops: Chap 5. 8 Design procedure -- example Synthesis using JK flip-flop: Fuw-Yi Yang 70

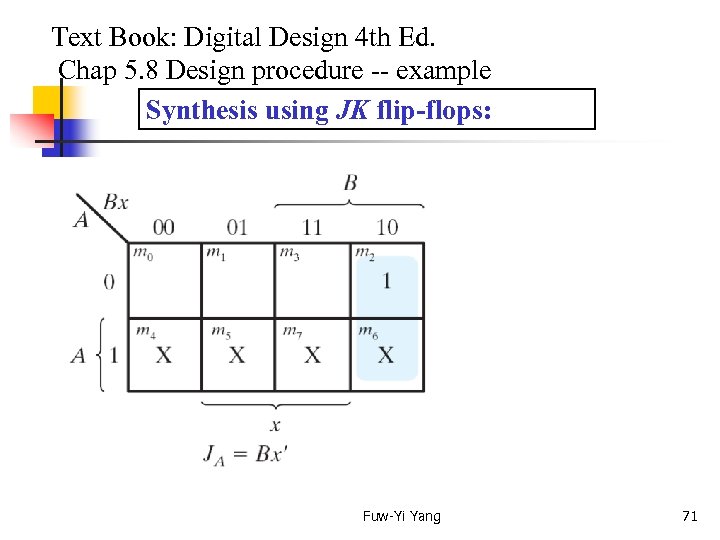
Text Book: Digital Design 4 th Ed. Chap 5. 8 Design procedure -- example Synthesis using JK flip-flops: Fuw-Yi Yang 71

Text Book: Digital Design 4 th Ed. Chap 5. 8 Design procedure -- example Synthesis using JK flip-flops: Fuw-Yi Yang 72

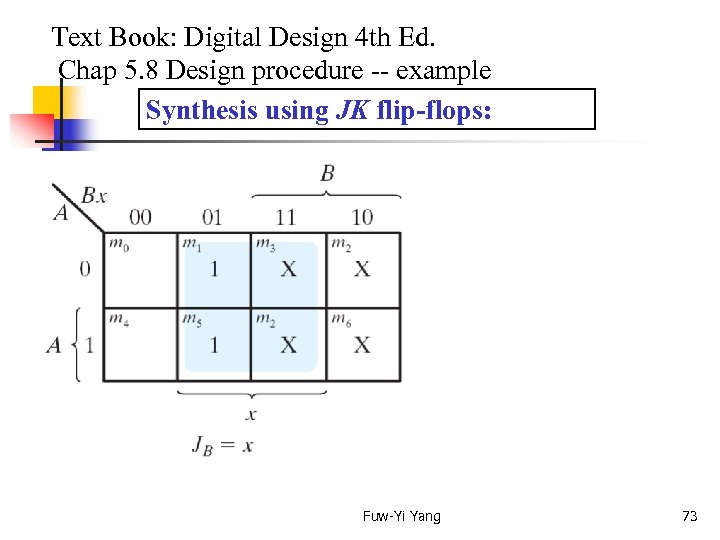
Text Book: Digital Design 4 th Ed. Chap 5. 8 Design procedure -- example Synthesis using JK flip-flops: Fuw-Yi Yang 73

Text Book: Digital Design 4 th Ed. Chap 5. 8 Design procedure -- example Synthesis using JK flip-flops: Fuw-Yi Yang 74

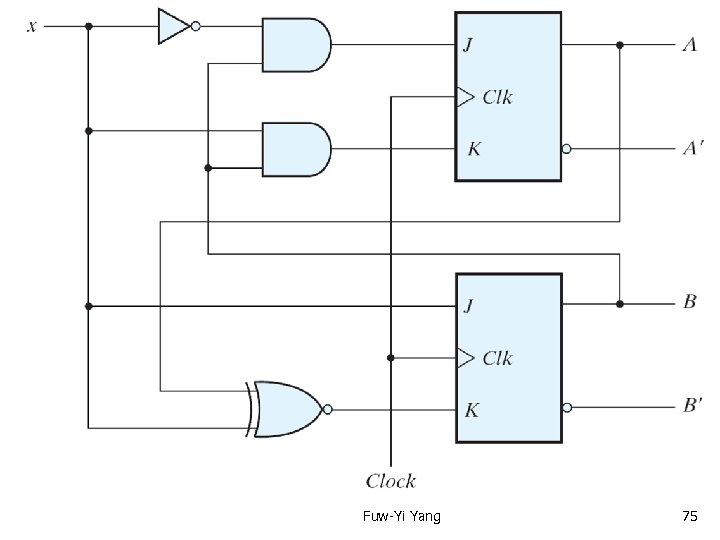
Fuw-Yi Yang 75

Text Book: Digital Design 4 th Ed. Chap 5. 8 Design procedure – another example Synthesis using T flip-flops Specification: Design a three bit binary counter. Fuw-Yi Yang 76

Fuw-Yi Yang 77

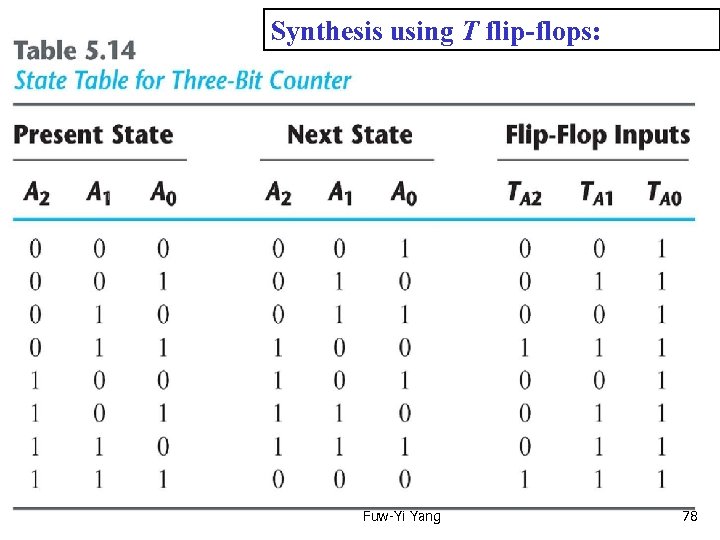
Synthesis using T flip-flops: Fuw-Yi Yang 78

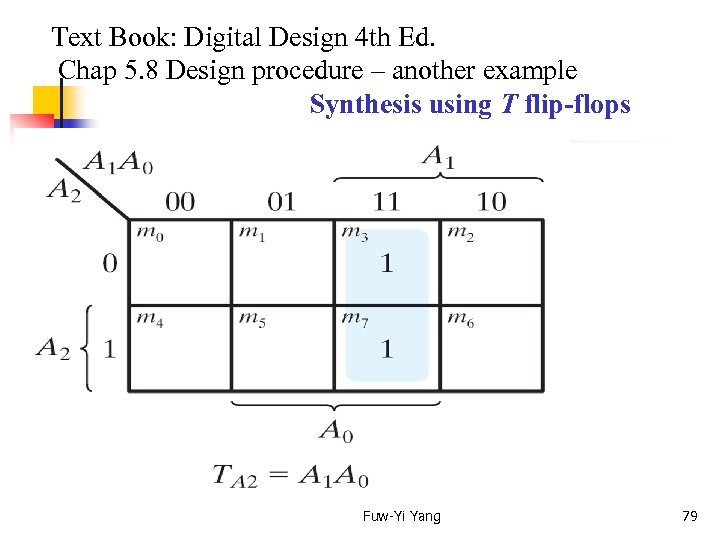
Text Book: Digital Design 4 th Ed. Chap 5. 8 Design procedure – another example Synthesis using T flip-flops Fuw-Yi Yang 79

Text Book: Digital Design 4 th Ed. Chap 5. 8 Design procedure – another example Synthesis using T flip-flops Fuw-Yi Yang 80

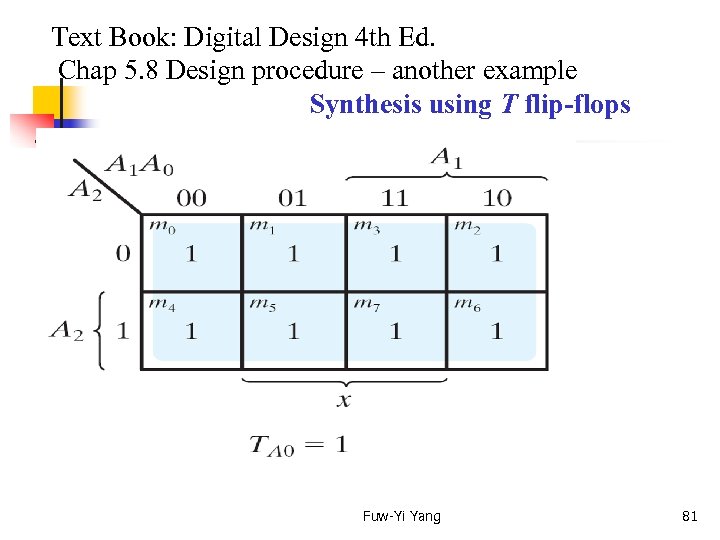
Text Book: Digital Design 4 th Ed. Chap 5. 8 Design procedure – another example Synthesis using T flip-flops Fuw-Yi Yang 81

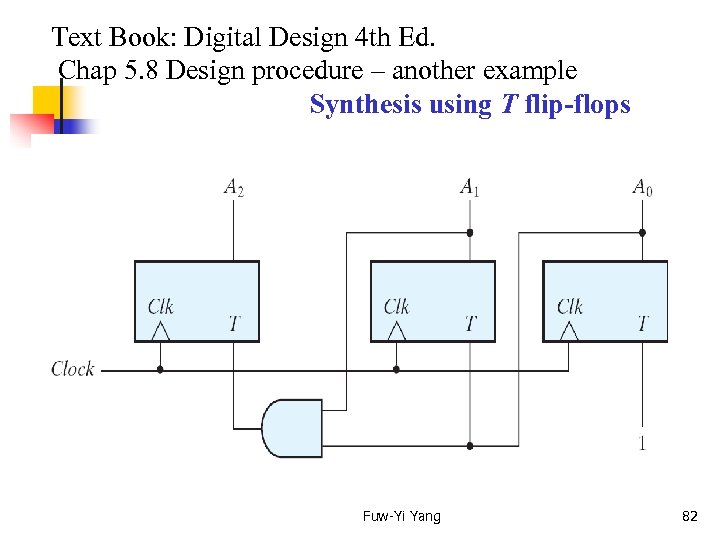
Text Book: Digital Design 4 th Ed. Chap 5. 8 Design procedure – another example Synthesis using T flip-flops Fuw-Yi Yang 82