我們在國小已經學過三角形的一些性質接著再來探討三角形的其他性質搭配課本第 98頁國小曾經利用量角器和剪紙拼湊的方法知道三角形的內角和為 180

我們在國小已經學過三角形的一些性質，接著再來探討三角形的其他性質。搭配課本第 98頁

國小曾經利用量角器和剪紙拼湊的方法，知道三角形的內角和為 180 度(平角)；現在我們透過摺紙的方式，將三角形的三個內角拼成一個平角。搭配課本第 98頁

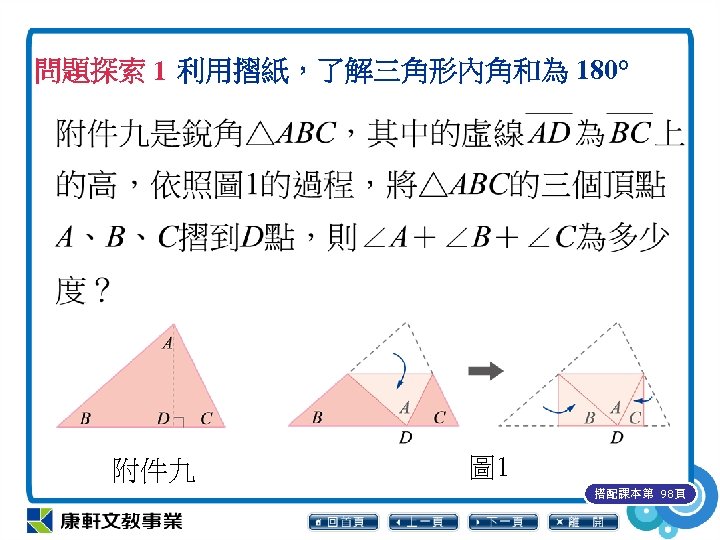
問題探索 1 利用摺紙，了解三角形內角和為 180° 附件九圖 1 搭配課本第 98頁

仿照問題探索 1 的方法，可否將直角三角形和鈍角三角形的三個內角拼成一個平角？可以。搭配課本第 98頁

由上可知：三角形內角和定理任意三角形的內角和為 180 度。搭配課本第 98頁

例 1 三角形內角和的應用有一個三角形，它的三個內角度數比為 1︰ 3︰ 5，則此三角形的最大角為多少度？搭配課本第 99頁

例 1 三角形內角和的應用搭配課本第 99頁

搭配課本第 99頁

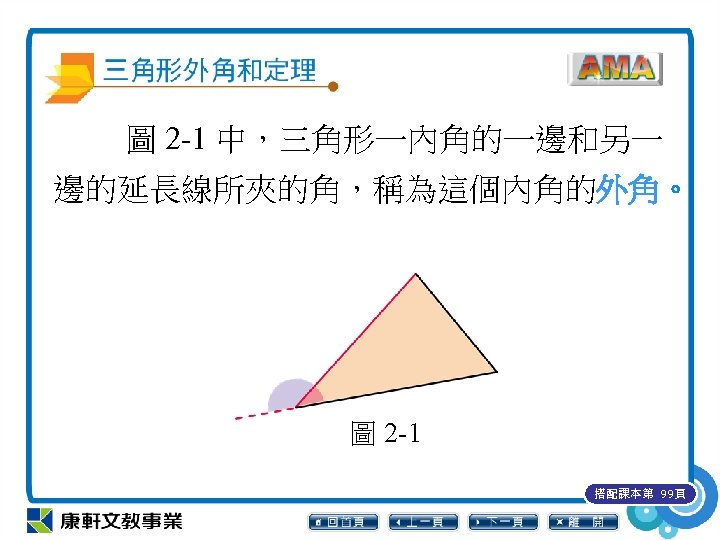
圖 2 -1 中，三角形一內角的一邊和另一邊的延長線所夾的角，稱為這個內角的外角。圖 2 -1 搭配課本第 99頁

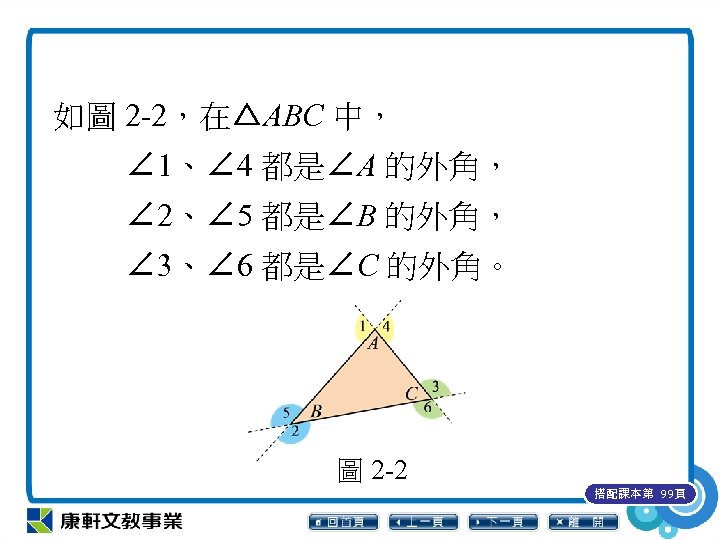
如圖 2 -2，在△ABC 中， ∠ 1、∠ 4 都是∠A 的外角， ∠ 2、∠ 5 都是∠B 的外角， ∠ 3、∠ 6 都是∠C 的外角。圖 2 -2 搭配課本第 99頁

根據圖 2 -2，可以得到 ∠A＋∠ 1＝ 180°，∠A＋∠ 4＝ 180°； ∠B＋∠ 2＝ 180°，∠B＋∠ 5＝ 180°； ∠C＋∠ 3＝ 180°，∠C＋∠ 6＝ 180°。由以上可知，對於任意三角形，每一個內角都與它的一個外角互補。搭配課本第 99頁

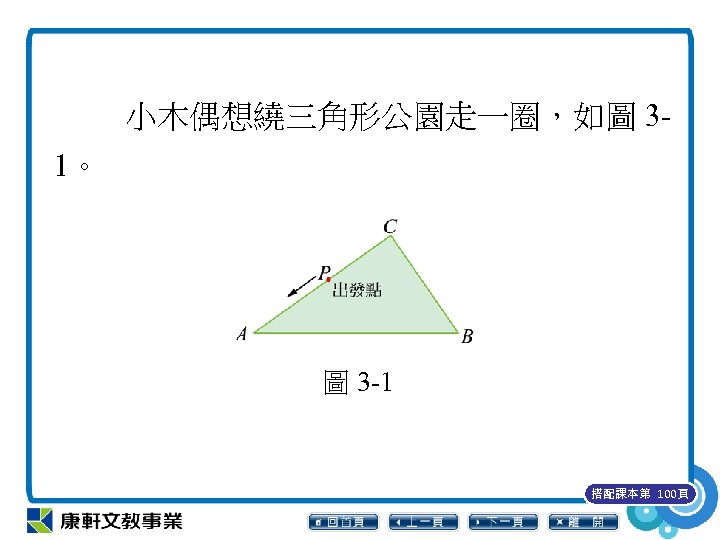
小木偶想繞三角形公園走一圈，如圖 31。圖 3 -1 搭配課本第 100頁

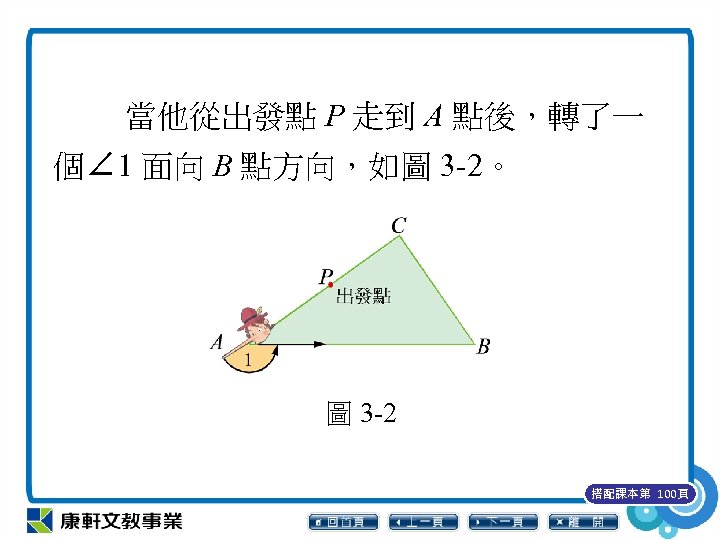
當他從出發點 P 走到 A 點後，轉了一個∠ 1 面向 B 點方向，如圖 3 -2。圖 3 -2 搭配課本第 100頁

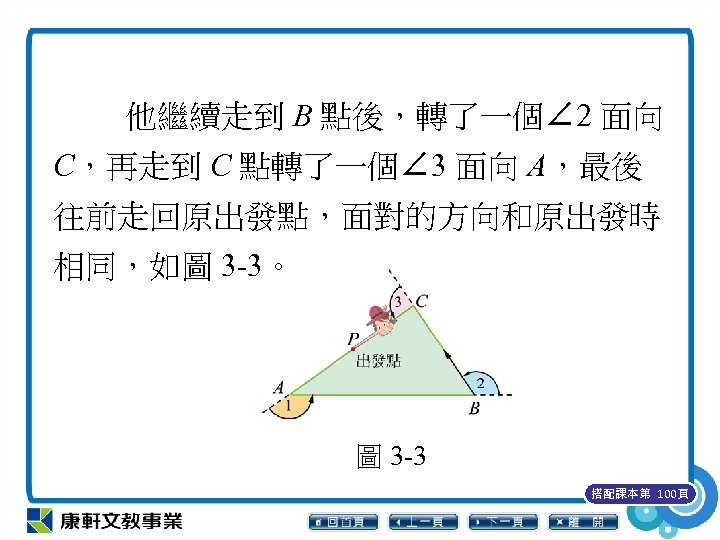
他繼續走到 B 點後，轉了一個∠ 2 面向 C，再走到 C 點轉了一個∠ 3 面向 A，最後往前走回原出發點，面對的方向和原出發時相同，如圖 3 -3。圖 3 -3 搭配課本第 100頁

由圖 3 -3 可知，小木偶所轉的∠ 1、∠ 2、 ∠ 3 分別是△ABC 三個內角的一個外角，我們稱∠ 1、∠ 2、∠ 3 是△ABC 的一組外角，小木偶走一圈所轉過的角度和正好與在固定一點轉一圈的度數是一樣的，都是 360°，因此∠ 1＋∠ 2＋∠ 3＝ 360°。搭配課本第 100頁

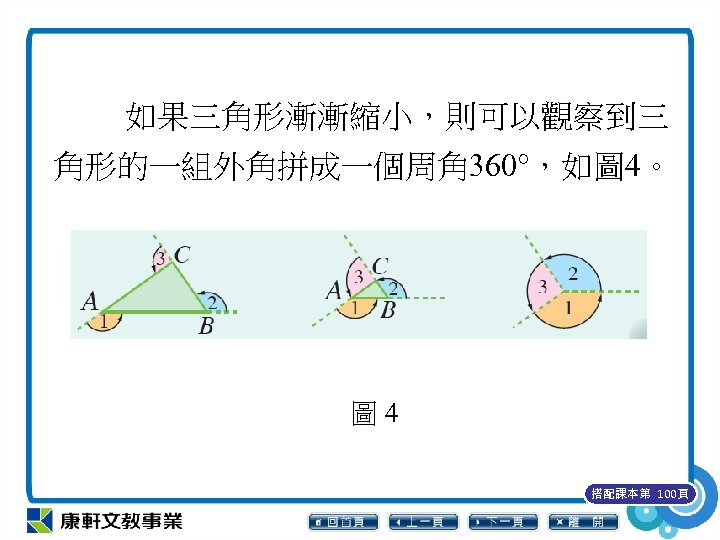
如果三角形漸漸縮小，則可以觀察到三角形的一組外角拼成一個周角 360°，如圖 4。圖 4 搭配課本第 100頁

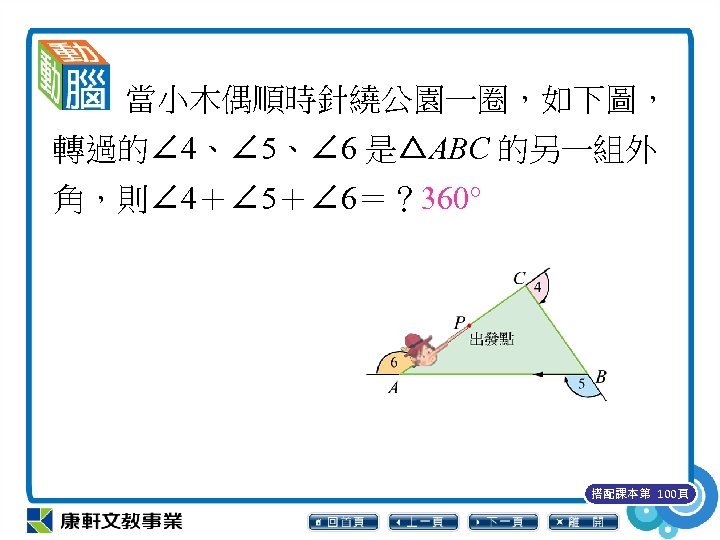
當小木偶順時針繞公園一圈，如下圖，轉過的∠ 4、∠ 5、∠ 6 是△ABC 的另一組外角，則∠ 4＋∠ 5＋∠ 6＝？ 360° 搭配課本第 100頁

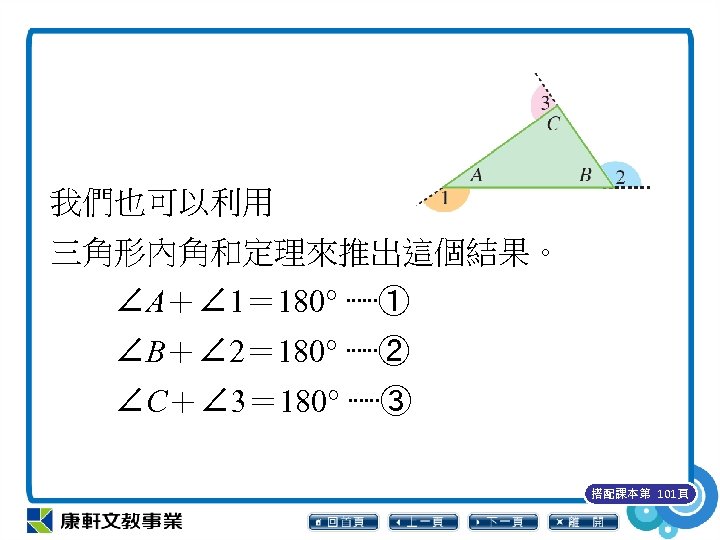
我們也可以利用三角形內角和定理來推出這個結果。　　∠A＋∠ 1＝ 180° ⋯⋯① 　　∠B＋∠ 2＝ 180° ⋯⋯② 　　∠C＋∠ 3＝ 180° ⋯⋯③ 搭配課本第 101頁

由①＋②＋③得 Hint 習慣上，我們會用符號「∵」表示「因為」，「∴」表示「所以」。 (∠A＋∠ 1)＋(∠B＋∠ 2)＋(∠C＋∠ 3) ＝ 180°× 3＝ 540° ∵∠A＋∠B＋∠C＝ 180° ∴∠ 1＋∠ 2＋∠ 3＝ 540°－180°＝ 360°。搭配課本第 101頁

三角形外角和定理任意三角形的一組外角和為 360 度。搭配課本第 101頁

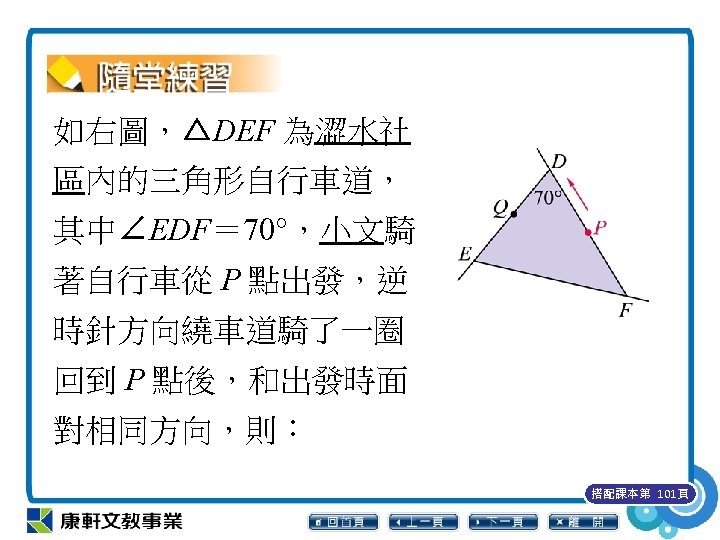
如右圖，△DEF 為澀水社區內的三角形自行車道，其中∠EDF＝ 70°，小文騎著自行車從 P 點出發，逆時針方向繞車道騎了一圈回到 P 點後，和出發時面對相同方向，則：搭配課本第 101頁

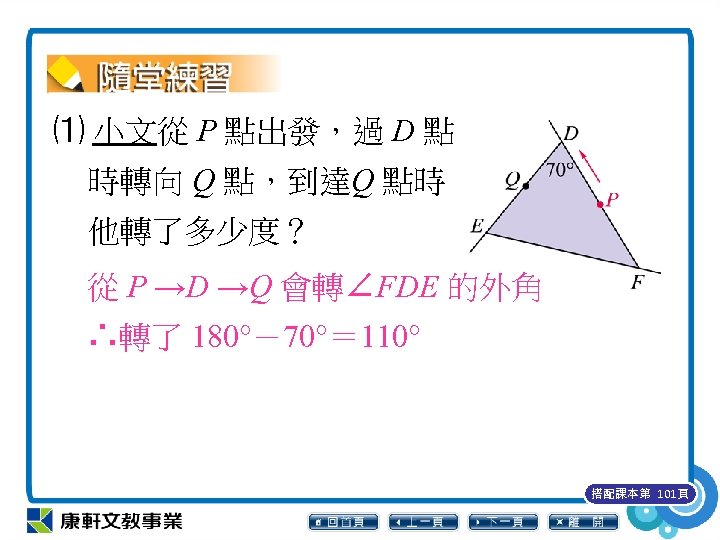
⑴ 小文從 P 點出發，過 D 點時轉向 Q 點，到達Q 點時他轉了多少度？從 P →D →Q 會轉∠FDE 的外角 ∴轉了 180°－70°＝ 110° 搭配課本第 101頁

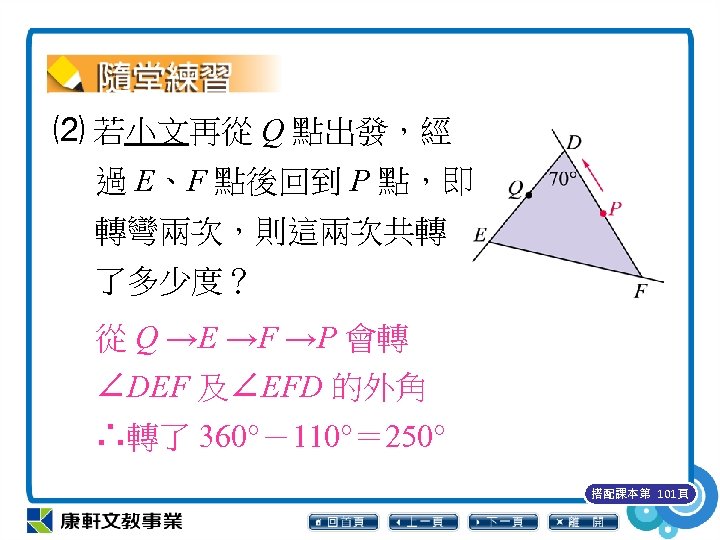
⑵ 若小文再從 Q 點出發，經過 E、F 點後回到 P 點，即轉彎兩次，則這兩次共轉了多少度？從 Q →E →F →P 會轉 ∠DEF 及∠EFD 的外角 ∴轉了 360°－110°＝ 250° 搭配課本第 101頁

例 2 內角和與外角和的應用有一個三角形，它的一組外角度數比為 2︰ 3︰ 3，寫出此三角形三個內角的度數。搭配課本第 102頁

例 2 內角和與外角和的應用 ∵三角形的一組外角和為 360°， ∴一組外角分別為：搭配課本第 102頁

例 2 內角和與外角和的應用 ∵三角形的每一個內角與它的一個外角互補， ∴三個內角分別為： 180°－90°＝ 90° 180°－135°＝ 45° 搭配課本第 102頁

若△ABC 為等腰三角形，其中頂角∠A＝ 70°，則底角∠B 的一個外角是多少度？ ∠B＝(180°－70°)÷ 2＝ 55° ∠B 的一個外角＝ 180°－55°＝ 125° 搭配課本第 102頁

是否有三角形的一組外角度數比為 1︰ 2︰ 3？搭配課本第 102頁

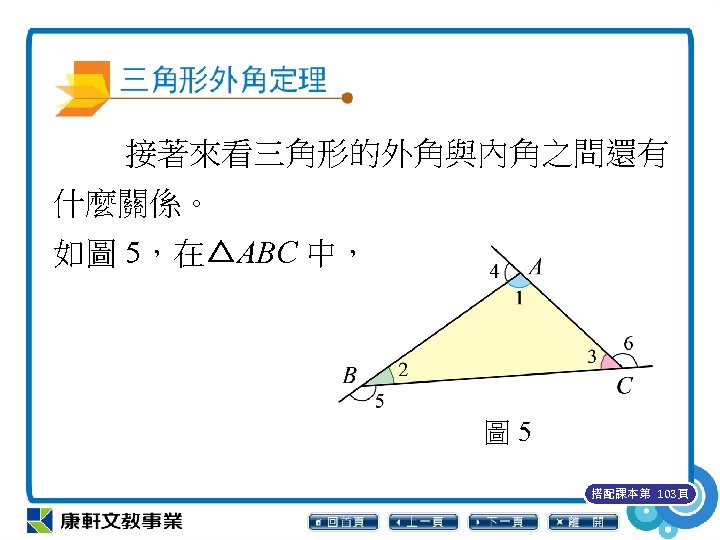
接著來看三角形的外角與內角之間還有什麼關係。如圖 5，在△ABC 中，圖 5 搭配課本第 103頁

∠ 1＋∠ 4＝ 180° ⋯⋯ ① (內角與它的外角互補) ∠ 1＋∠ 2＋∠ 3＝ 180° ⋯⋯ ② (三角形內角和為 180°) 由①、②可知︰∠ 1＋∠ 4＝∠ 1＋∠ 2＋∠ 3 所以∠ 4＝∠ 2＋∠ 3。搭配課本第 103頁

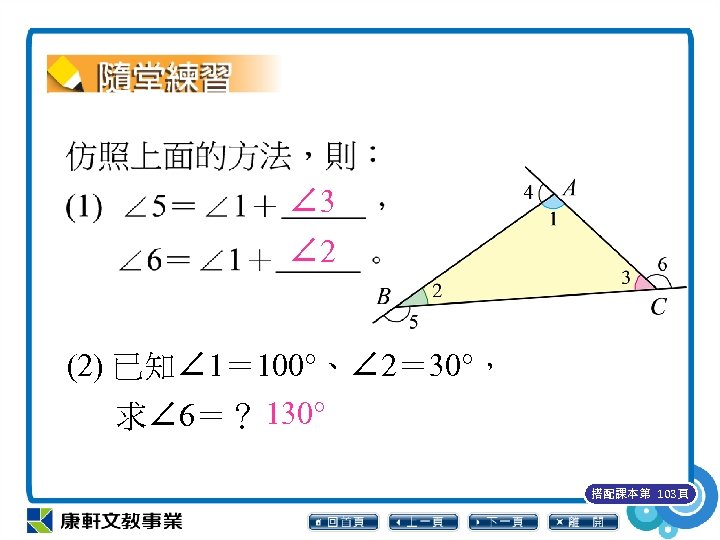
∠ 3 ∠ 2 (2) 已知∠ 1＝ 100°、∠ 2＝ 30°，求∠ 6＝？ 130° 搭配課本第 103頁

由上可知︰三角形外角定理三角形的任一外角等於其不相鄰兩內角的和。搭配課本第 103頁

例 3 三角形外角定理的應用 △ABC 中，若∠B 的外角是 110°，且 3∠C＝ 2∠A，則∠A 為多少度？設∠A＝x° 由三角形外角定理知： ∠A＋∠C＝ 110°， ∠C＝ 110°－∠A，搭配課本第 103頁

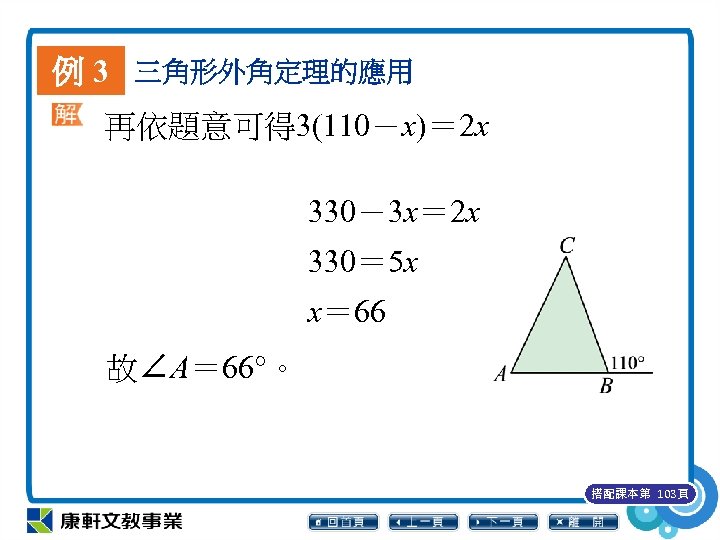
例 3 三角形外角定理的應用再依題意可得 3(110－x)＝ 2 x 330－3 x＝ 2 x 330＝ 5 x x＝ 66 故∠A＝ 66°。搭配課本第 103頁

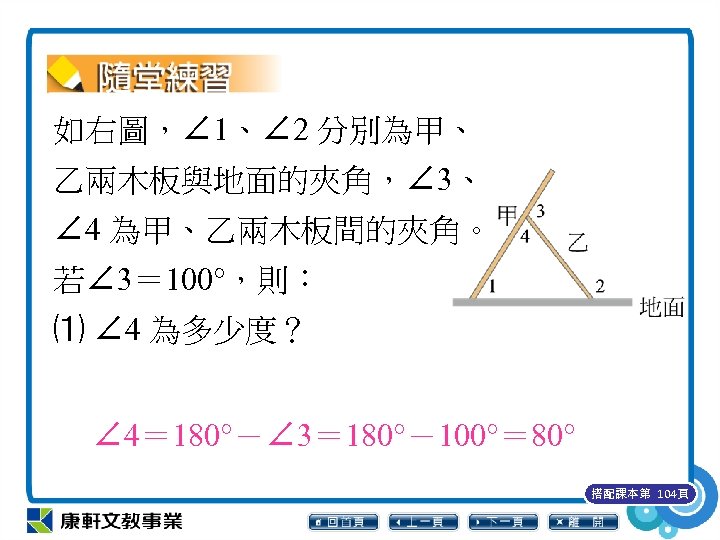
如右圖，∠ 1、∠ 2 分別為甲、乙兩木板與地面的夾角，∠ 3、 ∠ 4 為甲、乙兩木板間的夾角。若∠ 3＝ 100°，則： ⑴ ∠ 4 為多少度？ ∠ 4＝ 180°－∠ 3＝ 180°－100°＝ 80° 搭配課本第 104頁

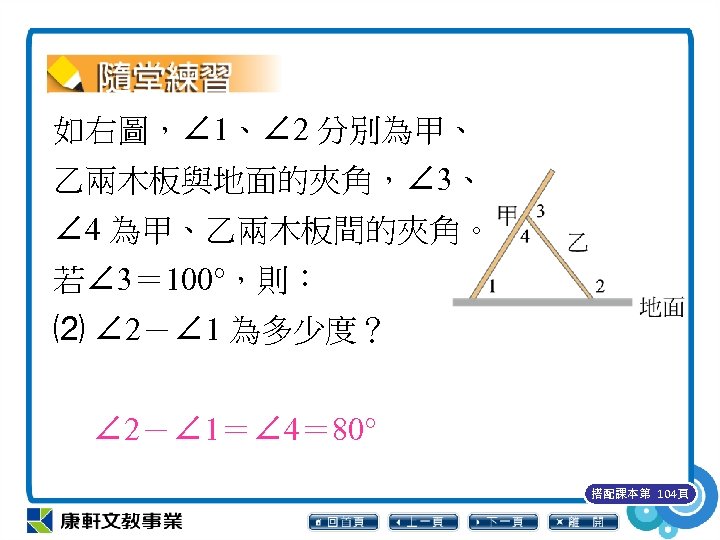
如右圖，∠ 1、∠ 2 分別為甲、乙兩木板與地面的夾角，∠ 3、 ∠ 4 為甲、乙兩木板間的夾角。若∠ 3＝ 100°，則： ⑵ ∠ 2－∠ 1 為多少度？ ∠ 2－∠ 1＝∠ 4＝ 80° 搭配課本第 104頁

例 4 三角形內角和定理或外角定理的應用搭配課本第 104頁

例 4 三角形內角和定理或外角定理的應用如右圖，利用三角形內角和定理︰在△ABO 中， ∠A＋∠B＋∠ 1＝ 180°，在△CDO 中， ∠C＋∠D＋∠ 2＝ 180°，得∠A＋∠B＋∠ 1＝∠C＋∠D＋∠ 2，又∠ 1＝∠ 2(對頂角相等)，故∠A＋∠B＝∠C＋∠D。搭配課本第 104頁

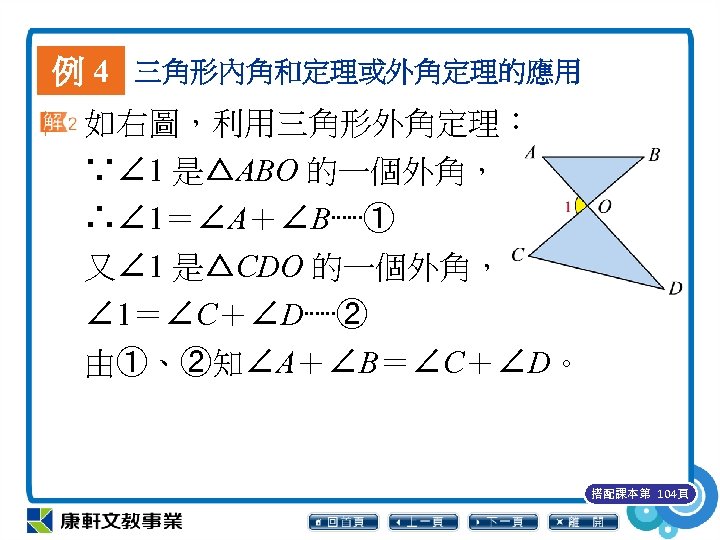
例 4 三角形內角和定理或外角定理的應用如右圖，利用三角形外角定理︰ ∵∠ 1 是△ABO 的一個外角， ∴∠ 1＝∠A＋∠B⋯⋯① 又∠ 1 是△CDO 的一個外角， ∠ 1＝∠C＋∠D⋯⋯② 由①、②知∠A＋∠B＝∠C＋∠D。搭配課本第 104頁

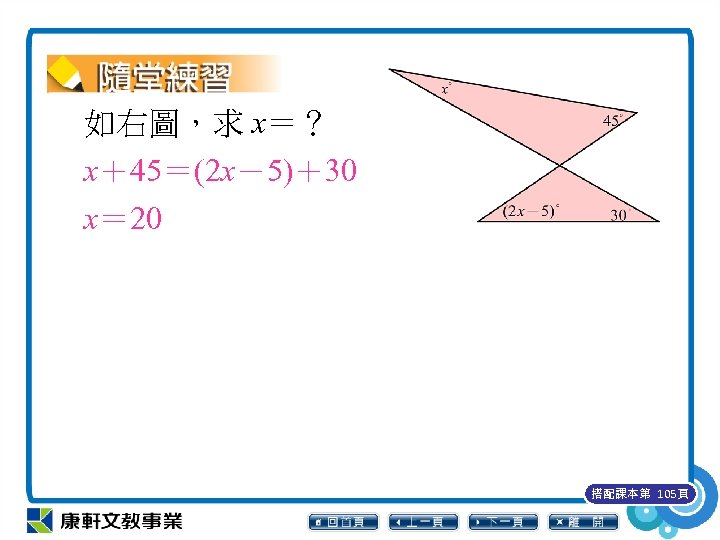
如右圖，求 x＝？ x＋45＝(2 x－5)＋30 x＝ 20 搭配課本第 105頁

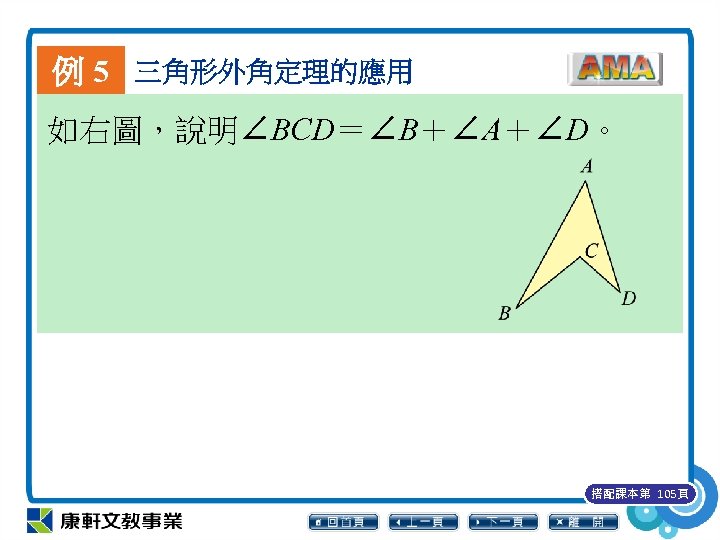
例 5 三角形外角定理的應用如右圖，說明∠BCD＝∠B＋∠A＋∠D。搭配課本第 105頁

例 5 三角形外角定理的應用 ⑵ ∵∠ 1 是△ABC 的一個外角，　 ∴∠ 1＝∠B＋∠ 3。　 ∵∠ 2 是△ADC 的一個外角，　 ∴∠ 2＝∠D＋∠ 4。 ⑶ ∠BCD＝∠ 1＋∠ 2 ＝∠B＋∠ 3＋∠ 4＋∠D ＝∠B＋∠A＋∠D。搭配課本第 105頁

在例 5 的解題過程中，我們在圖形上多作了一條射線 AC，像這樣在原圖形上所增添的射線(或直線、線段) ，就稱為輔助線。搭配課本第 105頁

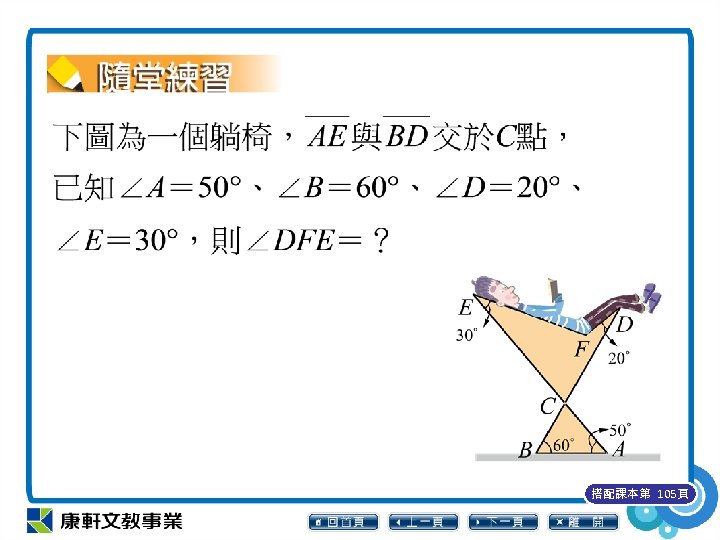
搭配課本第 105頁

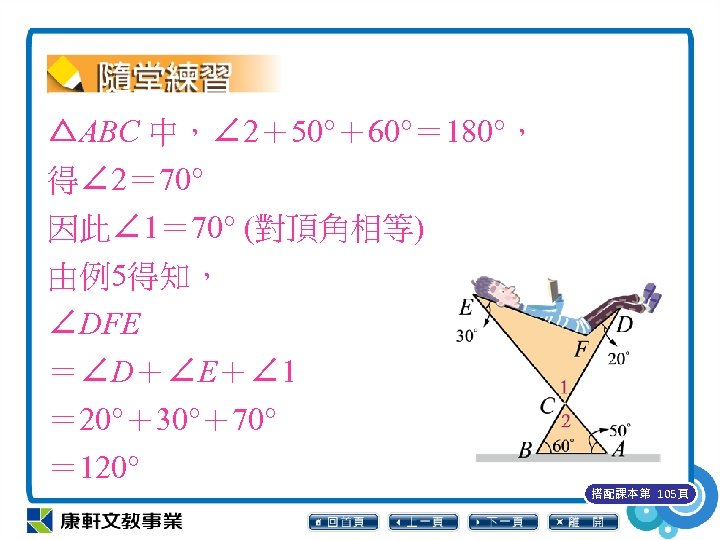
△ABC 中，∠ 2＋50°＋60°＝ 180°，得∠ 2＝ 70° 因此∠ 1＝ 70° (對頂角相等) 由例5得知， ∠DFE ＝∠D＋∠E＋∠ 1 ＝ 20°＋30°＋70° ＝ 120° 搭配課本第 105頁

主題 1 談到三角形的三個內角和是 180 度，接著我們利用這個性質來討論任意 n 邊形的內角和。搭配課本第 106頁

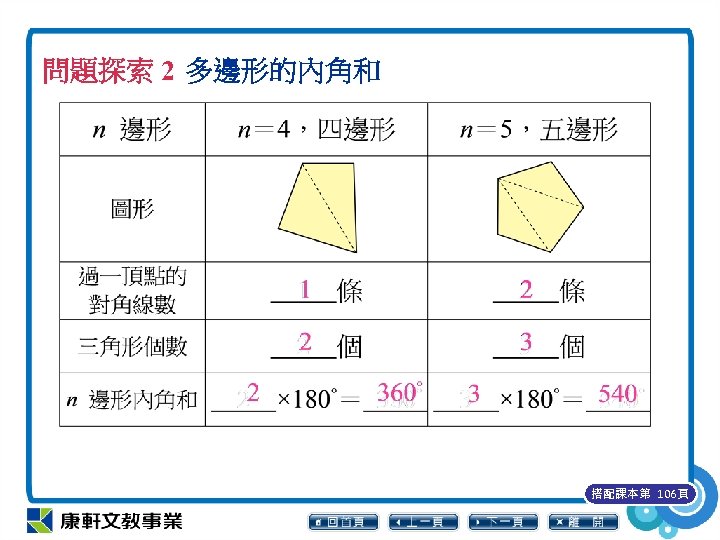
問題探索 2 多邊形的內角和 1. 有 n 個邊的多邊形稱為 n 邊形。在下列各 n 邊形中，由其中一個頂點向其他頂點畫對角線，並回答下列問題。搭配課本第 106頁

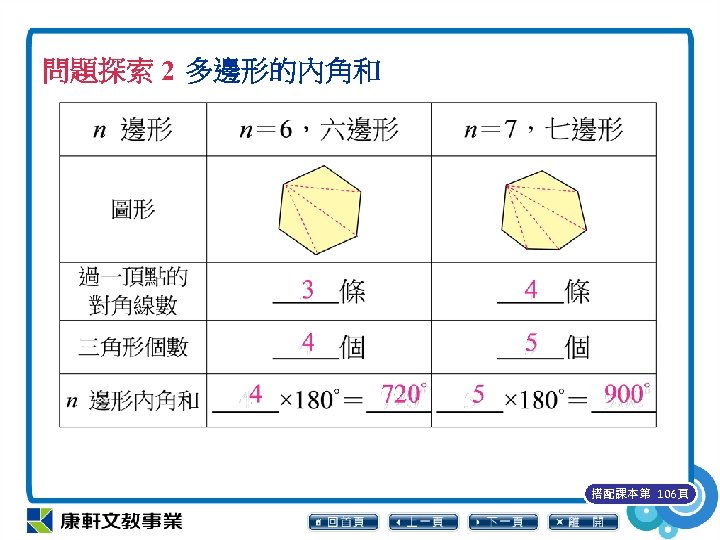
問題探索 2 多邊形的內角和搭配課本第 106頁

問題探索 2 多邊形的內角和 2. 過 n 邊形的某一個頂點向其他頂點可以連出幾條對角線？這些對角線可以將此 n 邊形分割成幾個三角形？可作(n－3)條對角線，分割成(n－2)個三角形搭配課本第 106頁

問題探索 2 多邊形的內角和 3. n 邊形的內角和等於幾個三角形的內角和？ (n－2)個三角形搭配課本第 106頁

由問題探索 2 可以得到：一個 n 邊形中，由其中一個頂點連接其他頂點，可以畫出(n－3)條對角線，並將此 n 邊形分割成(n－2)個三角形，因此： n 邊形內角和定理 n 邊形的內角和為(n－2) × 180°。搭配課本第 107頁

十二邊形的內角和為多少度？ (12－2)× 180°＝ 1800° 搭配課本第 107頁

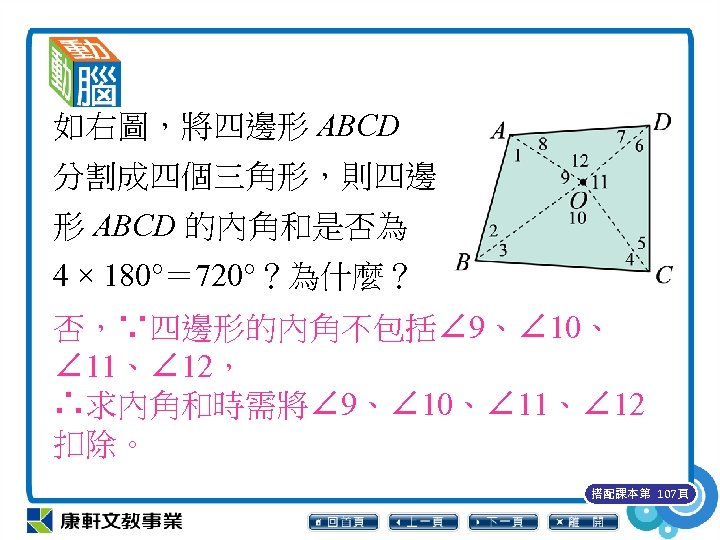
如右圖，將四邊形 ABCD 分割成四個三角形，則四邊形 ABCD 的內角和是否為 4 × 180°＝ 720°？為什麼？否，∵四邊形的內角不包括∠ 9、∠ 10、 ∠ 11、∠ 12， ∴求內角和時需將∠ 9、∠ 10、∠ 11、∠ 12 扣除。搭配課本第 107頁

對於一個 n 邊形，如果它的每一個邊長都相等且每一個內角也都相等，我們就稱它為正 n 邊形。正 n 邊形的內角搭配課本第 107頁

正十二邊形的每一個內角為幾度？搭配課本第 107頁

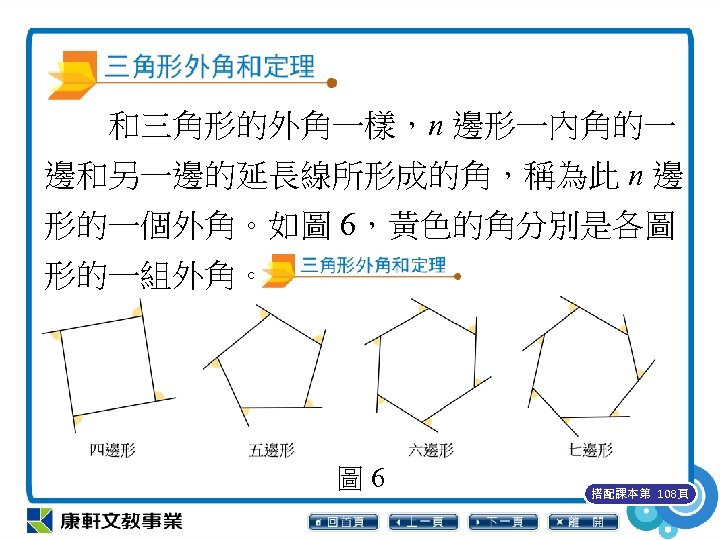
　　和三角形的外角一樣，n 邊形一內角的一邊和另一邊的延長線所形成的角，稱為此 n 邊形的一個外角。如圖 6，黃色的角分別是各圖形的一組外角。圖 6 搭配課本第 108頁

在圖 7 中，∠ 1、∠ 2、∠ 3、∠ 4 是四邊形 ABCD 的一組外角，仿照小木偶繞行三角形公園的方法，當以逆時針方向繞行四邊形公園一圈，小木偶共轉了一圈 360°，而鼻子所掃過的角度和剛好就是∠ 1、∠ 2、∠ 3、 ∠ 4 的和，所以∠ 1＋∠ 2＋∠ 3＋∠ 4＝ 360°，也就是說四邊形的一組外角和是 360°。搭配課本第 108頁

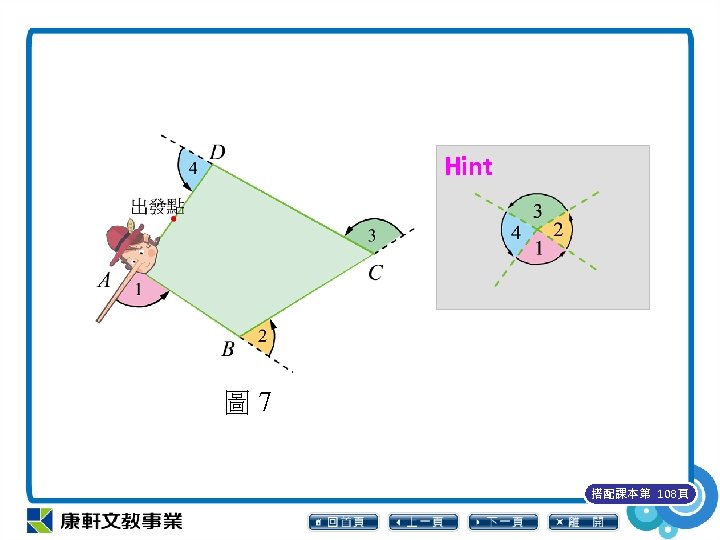
Hint 圖 7 搭配課本第 108頁

　　以上的作法可以推廣到其他的 n 邊形，當小木偶從出發點開始繞行 n 邊形一圈回到原出發點時，所轉的角度和是 n 邊形的一組外角和，而這一組外角和正好與在固定點轉一圈的度數是一樣的，所以我們可以得到︰ n 邊形外角和定理 n 邊形的一組外角和等於 360° 搭配課本第 108頁

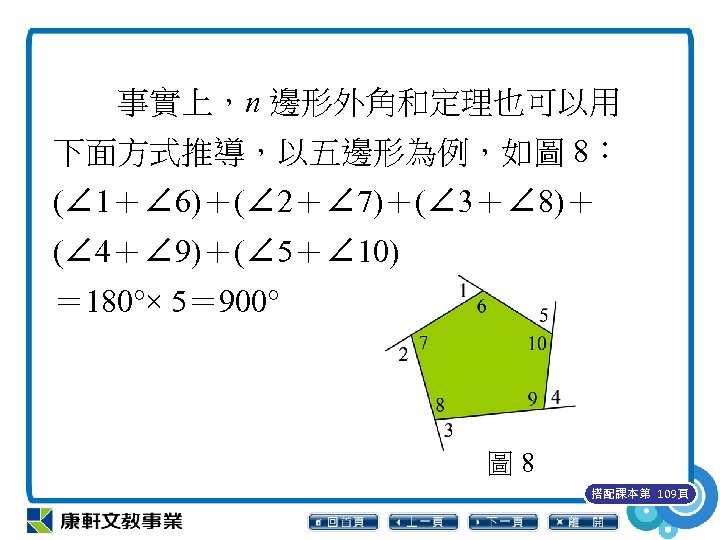
　　事實上，n 邊形外角和定理也可以用下面方式推導，以五邊形為例，如圖 8︰ (∠ 1＋∠ 6)＋(∠ 2＋∠ 7)＋(∠ 3＋∠ 8)＋ (∠ 4＋∠ 9)＋(∠ 5＋∠ 10) ＝ 180°× 5＝ 900° 圖 8 搭配課本第 109頁

(∠ 1＋∠ 2＋∠ 3＋∠ 4＋∠ 5)＋(∠ 6＋∠ 7＋∠ 8 ＋∠ 9＋∠ 10)＝ 900° ∵五邊形內角和為∠ 6＋∠ 7＋∠ 8＋∠ 9＋∠ 10 ＝(5－2) × 180°＝ 540°， ∴五邊形外角和為∠ 1＋∠ 2＋∠ 3＋∠ 4＋∠ 5 ＝ 900°－540°＝ 360°。搭配課本第 109頁

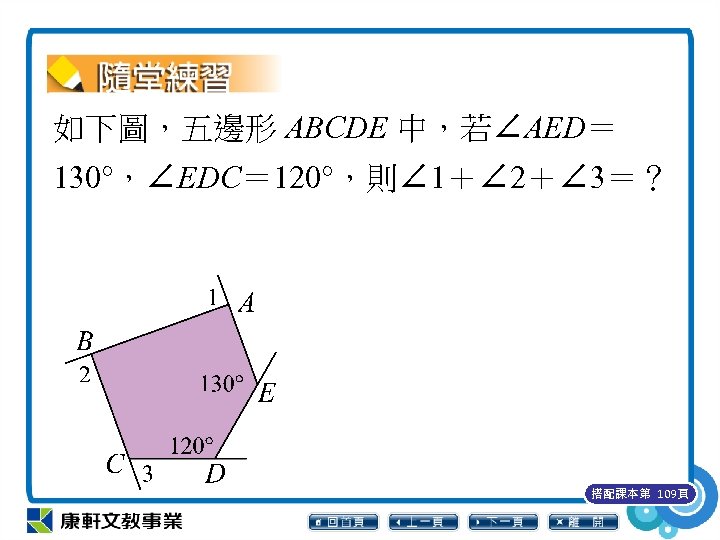
如下圖，五邊形 ABCDE 中，若∠AED＝ 130°，∠EDC＝ 120°，則∠ 1＋∠ 2＋∠ 3＝？搭配課本第 109頁

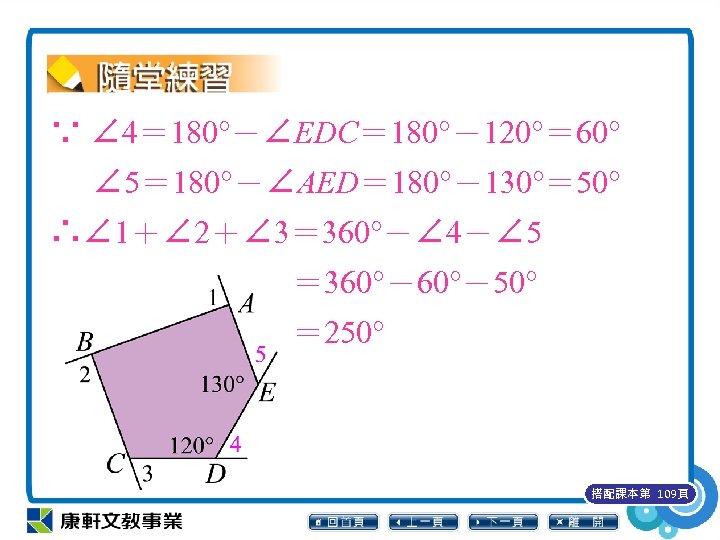
∵ ∠ 4＝ 180°－∠EDC＝ 180°－120°＝ 60° ∠ 5＝ 180°－∠AED＝ 180°－130°＝ 50° ∴∠ 1＋∠ 2＋∠ 3＝ 360°－∠ 4－∠ 5 　　　　　　＝ 360°－50° ＝ 250° 搭配課本第 109頁

我們知道正 n 邊形的每一個內角都相等，且每個內角與它的一個外角互補，因此每一個外角也相等，又外角和為 360°，所以可以得到：搭配課本第 109頁

正 n 邊形的外角與內角搭配課本第 109頁

∴這兩個式子是相同的搭配課本第 109頁

例 6 n 邊形內角和定理的應用若一正 n 邊形的每一個內角為 156°，則 n 是多少？ ∵正 n 邊形的內角和為(n－2) × 180°， (n－2) × 180＝ 156 × n n＝ 15。搭配課本第 110頁

例 6 n 邊形內角和定理的應用若一正 n 邊形的每一個內角為 156°，則 n 是多少？ ∵每一個內角為 156°， ∴每一個外角為 180°－156°＝ 24°，搭配課本第 110頁

1. 若正 n 邊形的一個內角是 144°，則： 36 　⑴ 每一個外角是度。 180°－144°＝ 36° 　⑵ n＝ 10 。 360°÷ 36°＝ 10 搭配課本第 110頁

2. 正十邊形的每一個外角度數是正五邊形的每一個外角度數的幾倍？搭配課本第 110頁

例 7 n 邊形內角和與比例問題有一個五邊形，它的內角度數比為 3︰ 4︰ 4︰ 4︰ 5，則這個五邊形的最大內角與最大外角各為幾度？搭配課本第 110頁

例 7 n 邊形內角和與比例問題 ⑴ 假設五個內角度數依序為 3 x、4 x、4 x、4 x、5 x 度，　 ∵五邊形的內角和度數為　(5－2) × 180＝ 540 (度)，　 ∴ 3 x＋4 x＋4 x＋4 x＋5 x＝ 540，得 x＝ 27。　最大內角度數為 5 x＝ 5 × 27＝ 135 (度)。搭配課本第 110頁

例 7 n 邊形內角和與比例問題 ⑵ ∵與最大外角相鄰的內角其度數最小，且最小內角度數為 3 x＝ 3 × 27＝ 81 (度)， ∴最大外角度數為 180－81＝ 99 (度)。搭配課本第 110頁

1. 若 n 邊形的內角和恰好是一組外角和的 5 倍，則 n 是多少？ (n－2) × 180＝ 360 × 5， n－2＝ 10， n＝ 12。搭配課本第 111頁

2. 若正 m 邊形的一個內角度數恰好是它一個外角度數的 5 倍，則 m 是多少？搭配課本第 111頁

例 8 n 邊形內角和與等差數列問題已知一個八邊形，其八個內角的度數由小到大排列恰好成等差數列，若其中最小的內角為 100°，則最大的內角為多少度？搭配課本第 111頁

例 8 n 邊形內角和與等差數列問題假設等差數列的首項為 100°，公差為 d °， ∵八邊形的內角和為(8－2) × 180°＝ 1080°，由等差級數的公式可知︰得 200＋7 d＝ 270，d＝ 10， ∴公差為 10 度。搭配課本第 111頁

例 8 n 邊形內角和與等差數列問題故最大內角a 8＝a 1＋(8－1)d ＝ 100＋7× 10＝ 170(度)。 Hint 搭配課本第 111頁

已知某 n 邊形，它的內角度數由小到大排列恰好成等差數列，若其中最小的內角為 50°，最大的內角為 166°，則 n 是多少？搭配課本第 111頁

此 n 邊形的內角和為(n－2)× 180度由等差級數求和的公式可知： 216 n＝ 360 n－720 故 n＝ 5 搭配課本第 111頁

1 三角形內角和定理與外角和定理 ⑴ 任意三角形的內角和為 180°。例如下圖， ∠A＋∠B＋∠C＝ 180° 搭配課本第 112頁

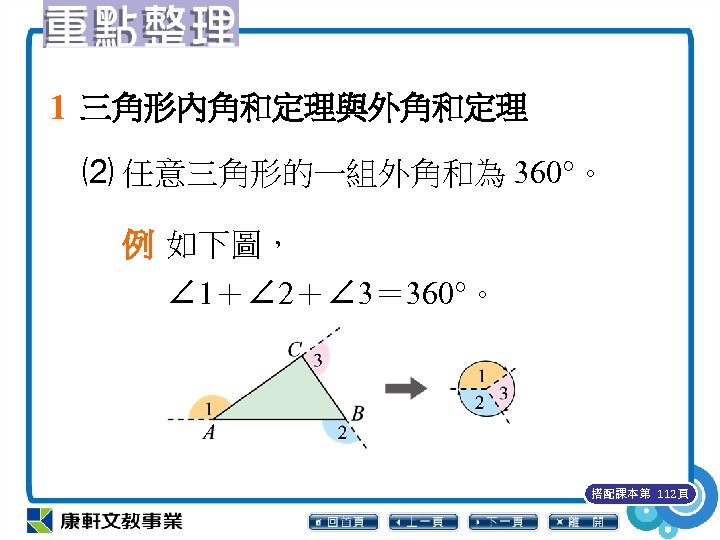
1 三角形內角和定理與外角和定理 ⑵ 任意三角形的一組外角和為 360°。例如下圖， ∠ 1＋∠ 2＋∠ 3＝ 360°。搭配課本第 112頁

2 三角形外角定理三角形的任一外角等於其不相鄰兩內角的和。例如右圖， ∠ 1＝∠ 2＋∠ 3。搭配課本第 112頁

3 n 邊形內角和定理 ⑴ 過 n 邊形的一個頂點，可以畫出 (n－3)條對角線，形成(n－2)個三角形。 ⑵ 任一 n 邊形的內角和為(n－2) × 180°。例如右圖，五邊形的內角和為 (5－2) × 180°＝ 540°。搭配課本第 112頁

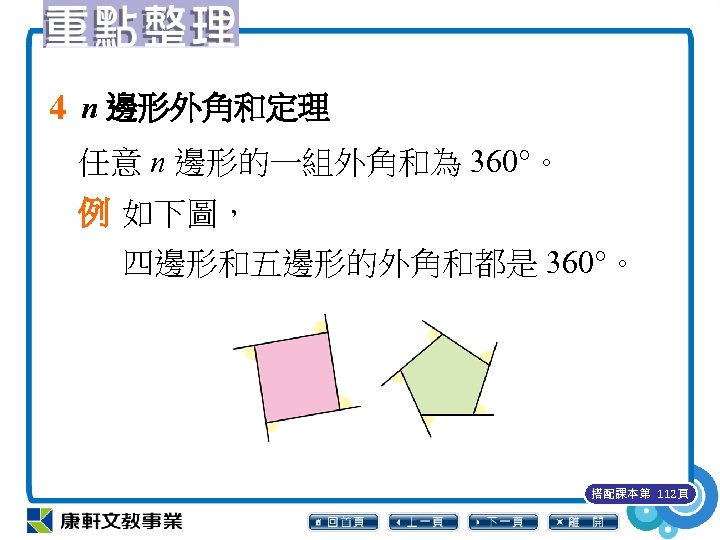
4 n 邊形外角和定理任意 n 邊形的一組外角和為 360°。例如下圖，四邊形和五邊形的外角和都是 360°。搭配課本第 112頁

5 正 n 邊形的外角與內角搭配課本第 112頁

5 正 n 邊形的外角與內角例 ⑵ 如右圖，正五邊形的每一個內角為 180°－72°＝ 108°。搭配課本第 112頁

1 △ABC 中，∠A＝ 85°、∠B＝(2 x＋15)°、 ∠C＝(x－10)°，則∠C＝？ ∵∠A＋∠B＋∠C＝ 180° 　85＋(2 x＋15)＋(x－10)＝ 180 　3 x＝ 180－90，得 x＝ 30 ∴∠C＝(30－10)°＝ 20° 搭配課本第 113頁

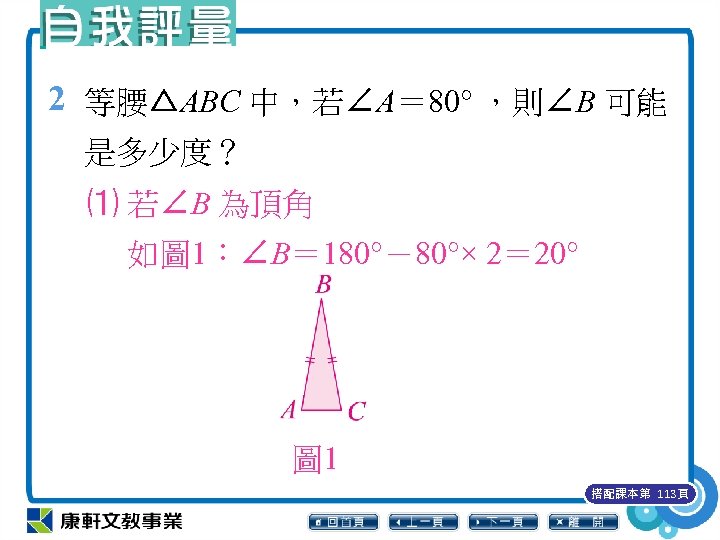
2 等腰△ABC 中，若∠A＝ 80° ，則∠B 可能是多少度？ ⑴ 若∠B 為頂角　如圖 1：∠B＝ 180°－80°× 2＝ 20° 圖 1 搭配課本第 113頁

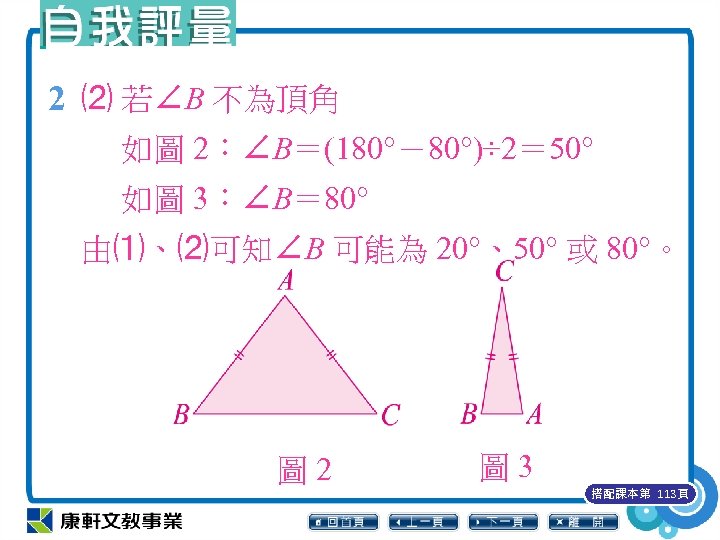
2 ⑵ 若∠B 不為頂角　如圖 2：∠B＝(180°－80°)÷ 2＝ 50° 　如圖 3：∠B＝ 80° 由⑴、⑵可知∠B 可能為 20°、50° 或 80°。圖 2 圖 3 搭配課本第 113頁

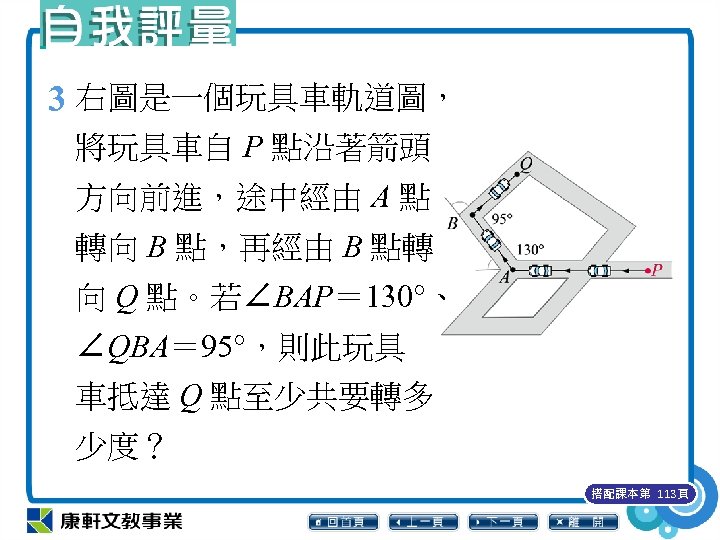
3 右圖是一個玩具車軌道圖，將玩具車自 P 點沿著箭頭方向前進，途中經由 A 點轉向 B 點，再經由 B 點轉向 Q 點。若∠BAP＝ 130°、 ∠QBA＝ 95°，則此玩具車抵達 Q 點至少共要轉多少度？搭配課本第 113頁

3 ∠BAP 的外角＝ 180°－∠BAP ＝ 180°－130°＝ 50° ∠QBA 的外角＝ 180°－∠QBA ＝ 180°－95° ＝ 85° ∴至少共要轉 50°＋85°＝ 135° 搭配課本第 113頁

4 搭配課本第 113頁

5 四邊形 ABCD 中，若 ∠A＝∠B＝ 3∠C＝ 3∠D，求： ⑴ ∠A 與∠C 的度數。設∠C＝x°，則∠A＝ 3 x°，∠B＝ 3 x°，∠D＝x° 3 x＋3 x＋x＋x＝ 360，x＝ 45 ∴∠C＝ 45°，∠A＝ 135° 搭配課本第 114頁

5 四邊形 ABCD 中，若 ∠A＝∠B＝ 3∠C＝ 3∠D，求： ⑵ ∠B 的外角與∠D 的外角的度數和。 ∠B＝ 135°，∴其外角＝ 45° ∠D＝ 45°，∴其外角＝ 135° 故∠B 的外角＋∠D 的外角＝ 180° 搭配課本第 114頁

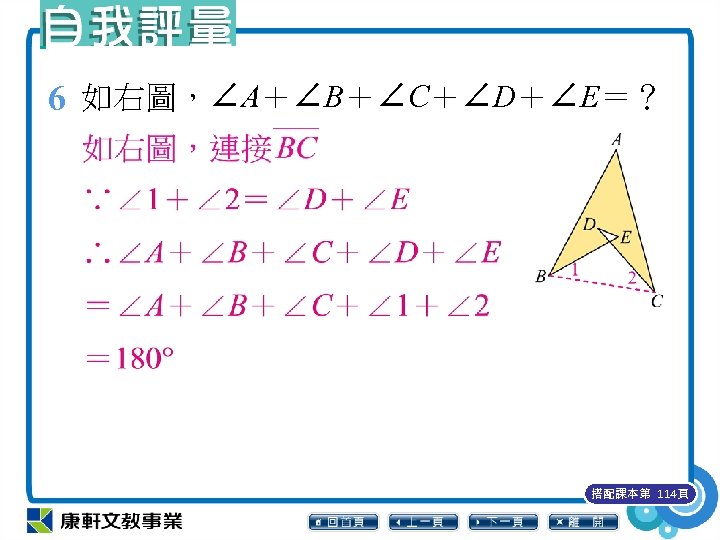
6 如右圖，∠A＋∠B＋∠C＋∠D＋∠E＝？搭配課本第 114頁

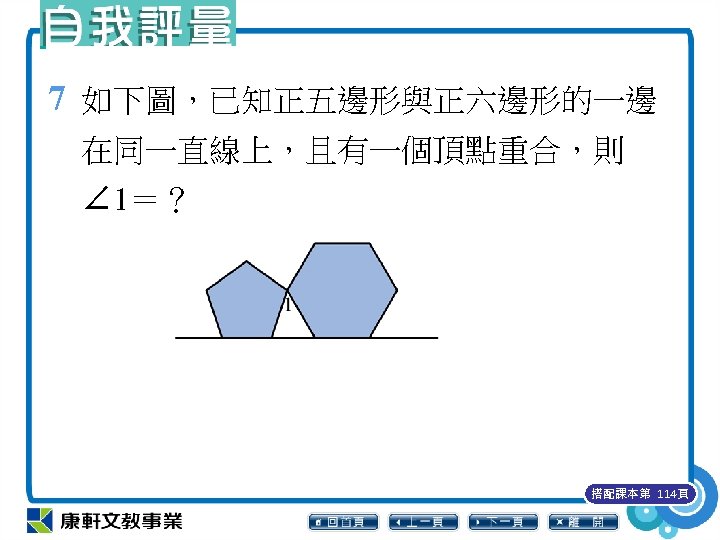
7 如下圖，已知正五邊形與正六邊形的一邊在同一直線上，且有一個頂點重合，則 ∠ 1＝？搭配課本第 114頁

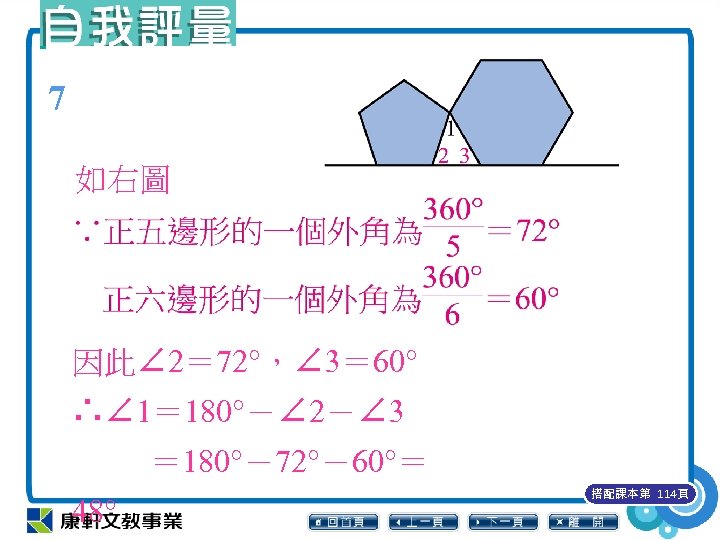
7 如右圖因此∠ 2＝ 72°，∠ 3＝ 60° ∴∠ 1＝ 180°－∠ 2－∠ 3 ＝ 180°－72°－60°＝ 48° 搭配課本第 114頁

我們在國小已經學過三角形的一些性質 接著再來探討三角形的其他性質 搭配課本第 98頁 國小曾經利用量角器和剪紙拼湊的方法 知道三角形的內角和為 180

我們在國小已經學過三角形的一些性質接著再來探討三角形的其他性質搭配課本第 98頁國小曾經利用量角器和剪紙拼湊的方法知道三角形的內角和為 180