669871408ed2b1caf5015ace8d48f737.ppt
- Количество слайдов: 39

情報 学概論 (アルゴリズムとデータ構造) 第 12回

動的計画法 (Dynamic Programming) • 分割統治法と同様,部分問題の解を統合する ことによって問題を解く. • 分割統治法では問題を独立な部分問題に分割し, 部分問題を再帰的に解き,それらの解を組み合わ せて元の問題の解を得る. • 動的計画法では部分問題が独立でないときに用い, 計算量を削減する. 2

動的計画アルゴリズムの開発 1. 2. 3. 4. 最適解の構造を特徴付ける 最適解の値を再帰的に定義する ボトムアップ方式で最適解の値を計算する 計算された情報からある最適解を構成する 3
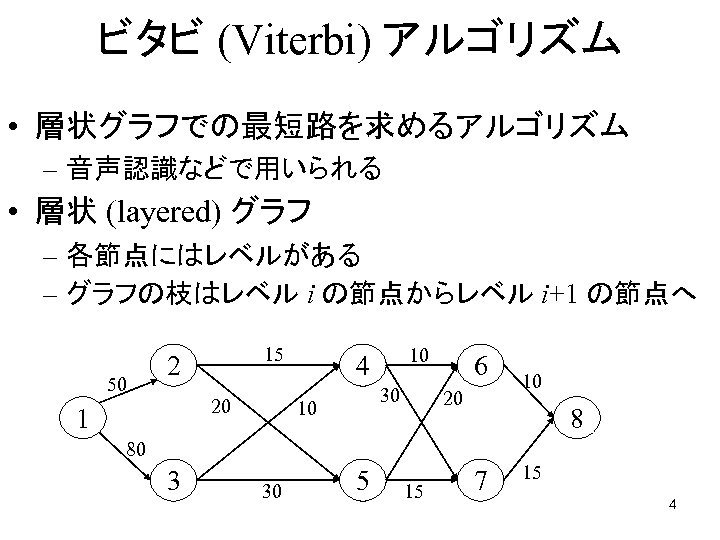
ビタビ (Viterbi) アルゴリズム • 層状グラフでの最短路を求めるアルゴリズム – 音声認識などで用いられる • 層状 (layered) グラフ – 各節点にはレベルがある – グラフの枝はレベル i の節点からレベル i+1 の節点へ 50 15 2 20 1 10 4 30 10 6 20 10 8 80 3 30 5 15 7 15 4

• レベル数を l, 各レベル内の節点数を k とすると – n = kl – m = k 2 l • 始点から終点までのパスの数は kl • 始点からレベル i+1 の節点までの最短路は, 始点からレベル i のある節点までの最短路に 枝を 1つ追加したもの • レベル i+1 の全節点への最短路は O(k 2) 時間で 求まる • 全レベルでO(k 2 l) = O(m) 時間 • ダイクストラ法よりも簡単で計算量も小さい 5

最長共通部分系列 (Longest Common Subsequence) S 1=ACCGGTCGAGTGCGCGGAAGCCGAA S 2=GTCGTTCGGAATGCCGTTGCTCTGTAAA S 3=GTCGTCGGAAGCCGAA • 系列 A が系列 B の部分系列であるとは,B から 0 個以上の要素を取り去ると A になること • S 3 は S 1 と S 2 両方の部分系列の中で最長 • 最長共通部分系列を動的計画法で求める 6

1. 最長共通部分系列の特徴付け • LCS(X, Y) を力づく (brute-force) で解く場合 – X の全ての部分系列を生成し,それらが Y の 部分系列になっているか1つずつ調べる – X の長さを m とすると,部分系列の数は 2 m 個 – 遅すぎる • X = <x 1, x 2, …, xm> とする • X の i 番目の接頭語 (prefix) を Xi = <x 1, x 2, …, xi> と定義する 7

• 定理 (LCSの部分構造最適性) X = <x 1, x 2, …, xm> と Y = <y 1, y 2, …, yn> のLCSを Z = <z 1, z 2, …, zk> とすると 1. xm= yn ならば zk= xm= yn かつ Zk 1 は Xm 1 と Yn 1 のLCSである 2. xm yn かつ zk xm ならば Z は Xm 1 と Y のLCSである 3. xm yn かつ zk yn ならば Z は X と Yn 1 のLCSである 8

証明: (1) zk xm を仮定すると,Z に xm= yn を付け 加えて X と Y の共通部分系列で長さ k+1 のものを 得られるが,これは Z = LCS(X, Y) という仮定に矛盾 . 接頭語 Zk 1 は Xm 1 と Yn 1 の長さ k 1 の共通部分 系列だが,これが最長であることを背理法で示す. 長さが k 以上の Xm 1 と Yn 1 の共通部分系列 W が 存在すると仮定する.W に xm= yn を付加すると X と Y の共通部分系列で長さ k+1 以上のものが作れ, 矛盾. 9

(2) zk xm ならば, Z は Xm 1 と Y の共通部分系列 である.Xm 1 と Y の共通部分系列 W で長さが k+1 以上のものが存在すると仮定すると,W は Xm と Y の共通部分系列でもあるから,Z = LCS(X, Y) という 仮定に矛盾. (3) (2) と同様. 2つの系列のLCSは,その一部としてそれらの接頭語 のLCSを含んでいることがわかる.従って,LCS問題 は部分構造最適性を持つ. 10

2. 再帰的な解 • X = <x 1, x 2, …, xm> と Y = <y 1, y 2, …, yn> のLCSを 求めるとき • xm= yn ならば Xm 1 と Yn 1 のLCSが必要 • xm yn ならば 2つの部分問題を解く必要がある – Xm 1 と Y のLCS – X と Yn 1 のLCS – 得られた 2つのLCSの長い方が X と Y のLCS • Xi と Yj のLCSの長さを c[i, j] とすると 11
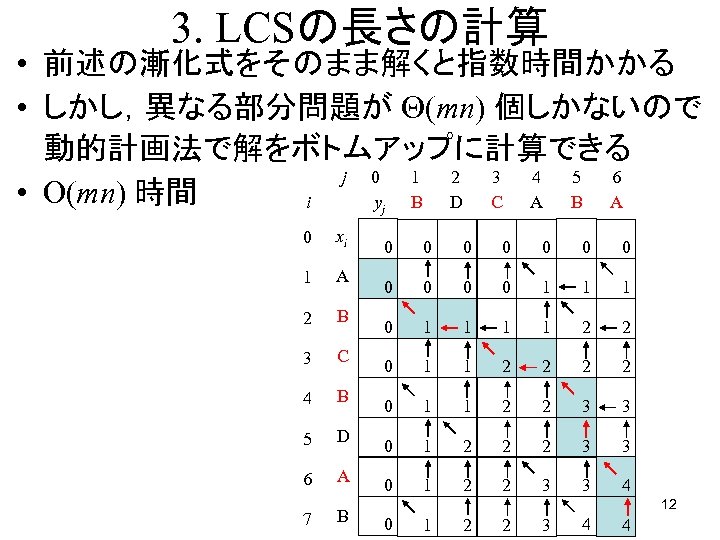
3. LCSの長さの計算 • 前述の漸化式をそのまま解くと指数時間かかる • しかし,異なる部分問題が (mn) 個しかないので 動的計画法で解をボトムアップに計算できる j 0 1 2 3 4 5 6 • O(mn) 時間 i y B D C A B A j 0 xi 1 A 2 B 3 C 4 B 5 D 6 A 7 B 0 0 0 1 1 1 1 2 2 0 1 1 2 2 3 3 0 1 2 2 3 3 4 12 0 1 2 2 3 4 4
![4. LCSの構成 • c[m, n] の値が X と Y のLCSの長さを表す • 表中の矢印がLCSの解を表す – 「↑」はLCSに 4. LCSの構成 • c[m, n] の値が X と Y のLCSの長さを表す • 表中の矢印がLCSの解を表す – 「↑」はLCSに](https://present5.com/presentation/669871408ed2b1caf5015ace8d48f737/image-13.jpg)
4. LCSの構成 • c[m, n] の値が X と Y のLCSの長さを表す • 表中の矢印がLCSの解を表す – 「↑」はLCSに xi を含めないことを表す – 「←」はLCSに yj を含めないことを表す – 斜めはLCSに xi = yj を含めることを表す • [m, n] のマスから矢印をたどれば解が求まる • O(m+n) 時間 • 全体で O(mn) 時間 13

文字列の編集距離 • 文字列 X と Y の編集距離 (edit distance) とは, X に以下の編集操作を繰り返して Y に変換する 際の最小の操作回数である. – 挿入: xi と xi+1 の間に文字 c を入れる – 削除: xi を削除 – 置換: xi を文字 c で置き換える X = ACGTT A を削除 CGTT C を挿入 編集距離 = 3 CGCTT T を A に置換 Y = CGCAT 14

• X の文字を削除する代わりに,Y に gap (空白) を入れる • X に文字を挿入するときは必ず Y の文字を入れる ことになる ⇒ X に gap を入れる • X と Y に gap を入れた X’ と Y’ で,ミスマッチの数 を最小にする問題と等価 • LCS問題に似ている X = ACGTT Y = CGCAT X’ = ACG TT Y’ = CGCAT ミスマッチ = 3 15

• Xi = <x 1, x 2, …, xi> と Yj = <y 1, y 2, …, yj> の 編集距離を c[i, j] とする • xi と yj をマッチさせる場合 – xi= yj ならば c[i, j] = c[i 1, j 1] – xi yj ならば c[i, j] = c[i 1, j 1]+1 • xi の次に gap を入れ yj とマッチさせる場合 – c[i, j] = c[i, j 1]+1 • yj の次に gap を入れ xi とマッチさせる場合 – c[i, j] = c[i 1, j]+1 • c[i, j] はこれら3つの中の最小値 • O(mn) 時間 (m = |X|, n= |Y|) 16
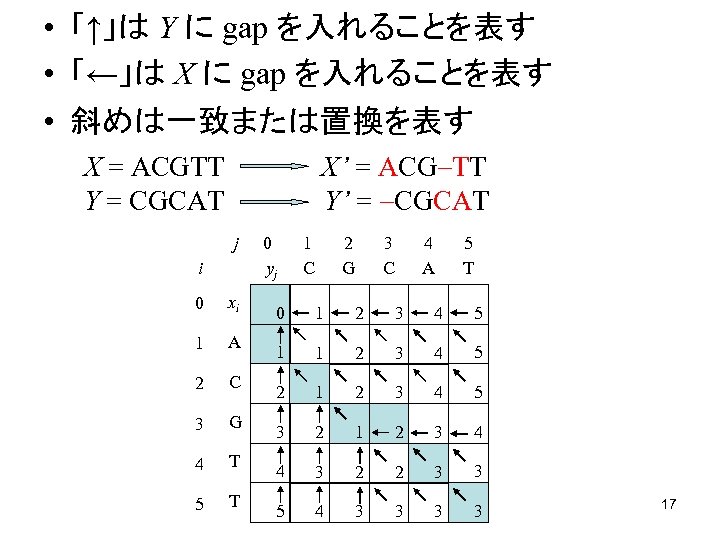
• 「↑」は Y に gap を入れることを表す • 「←」は X に gap を入れることを表す • 斜めは一致または置換を表す X = ACGTT Y = CGCAT X’ = ACG TT Y’ = CGCAT j i 0 xi 1 A 2 C 3 G 4 T 5 T 0 yj 1 C 2 G 3 C 4 A 5 T 0 1 2 3 4 5 1 1 2 3 4 5 2 1 2 3 4 5 3 2 1 2 3 4 4 3 2 2 3 3 5 4 3 3 17
![関係データベース 年齢が7歳から47歳である Age ∈ [7, 47] 携帯電話を持っている cell phone = yes 18 関係データベース 年齢が7歳から47歳である Age ∈ [7, 47] 携帯電話を持っている cell phone = yes 18](https://present5.com/presentation/669871408ed2b1caf5015ace8d48f737/image-18.jpg)
関係データベース 年齢が7歳から47歳である Age ∈ [7, 47] 携帯電話を持っている cell phone = yes 18
![1次元数値属性相関ルール C 1 ⇒C 2 ( A 1 ∈ [v 1 , v 2] ) 1次元数値属性相関ルール C 1 ⇒C 2 ( A 1 ∈ [v 1 , v 2] )](https://present5.com/presentation/669871408ed2b1caf5015ace8d48f737/image-19.jpg)
1次元数値属性相関ルール C 1 ⇒C 2 ( A 1 ∈ [v 1 , v 2] ) ⇒ ( A 2 = yes ) Age ∈ [7, 47] salary ∈ [100, 300] Age ∈ [45, 90] cell phone = yes house = yes 19
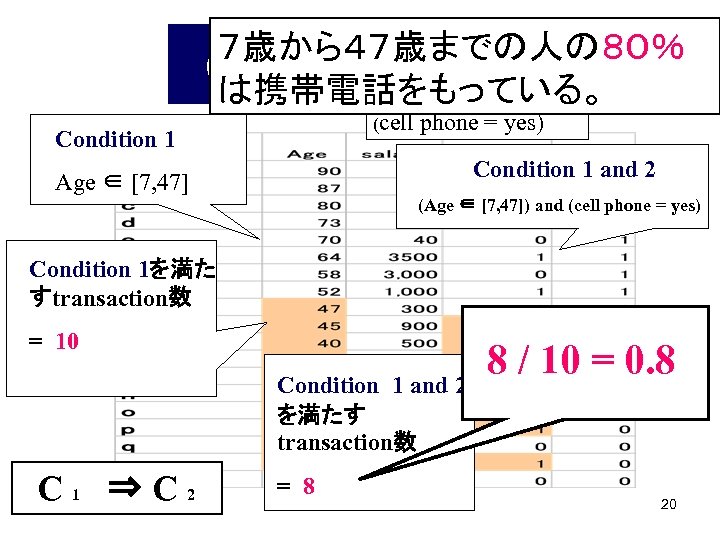
7歳から47歳までの人の80% Condition 2 は携帯電話をもっている。 Confidence (cell Condition 1 phone = yes) Age ∈ [7, 47] Condition 1 and 2 (Age ∈ [7, 47]) and (cell phone = yes) Condition 1を満た すtransaction数 = 10 Condition 1 and 2 を満たす transaction数 C 1 ⇒C 2 = 8 8 / 10 = 0. 8 20

45歳から90歳まで人の30%は Condition 2 携帯電話をもっている。 Confidence (cell Condition 1 phone = yes) Age ∈ [45, 90] Condition 1 and 2 Age ∈ [45, 90] and (cell phone = yes) Condition 1を満た すtransaction数 = 10 Condition 1 and 2 を満たす transaction数 C 1 ⇒C 2 = 3 3 / 10 = 0. 3 21

Confidence and Support( C 1 ) : 条件C 1 を満たすタプル の割合 Conf( C 1 ⇒ C 2) : Support( C C ) 1 ∧ 2 ( Condition 1 and 2 を満たすタプル数 ) ( Condition 1 を満たすタプル数) 1 Support( C ) 22

最適相関ルール発見問題 • 最適確信度相関ルール – support(C 1) minsup であるルールのうち,conf( C 1 ⇒ C 2) が最大であるものを求める • 最適支持度相関ルール – conf( C 1 ⇒ C 2) minconf であるルールのうち, support(C 1) が最大であるものを求める • 最適ゲイン相関ルール – conf( C 1 ⇒ C 2) support(C 1) を最大にするルー ルを求める 23

数値属性結合ルールの発見 • 確信度がminconf以上で,支持度が最大とな る領域を求める • 領域は矩形和楕円型領域とする 24
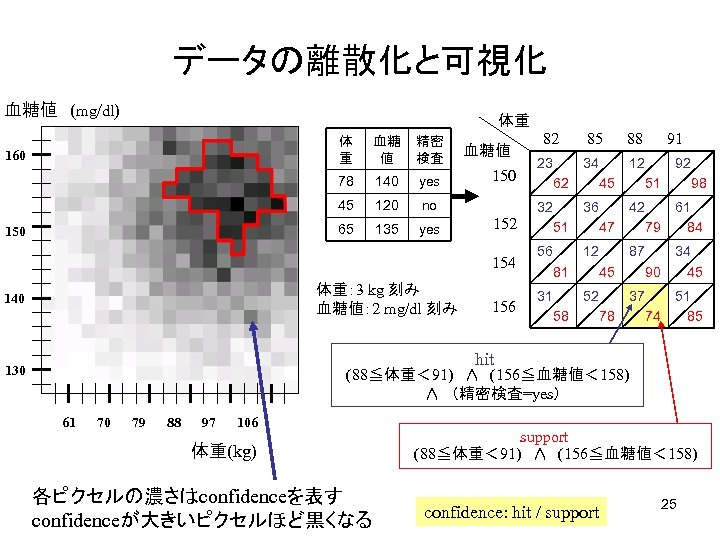
データの離散化と可視化 血糖値 (mg/dl) 体重 160 血糖 値 精密 検査 78 yes 45 120 135 yes 体重: 3 kg 刻み 血糖値: 2 mg/dl 刻み 140 85 88 150 23 62 34 45 12 51 92 98 152 32 51 36 47 42 79 61 84 56 81 12 45 87 90 34 45 156 31 58 52 78 37 74 51 85 血糖値 no 65 150 140 82 154 体 重 91 hit 130 (88≦体重< 91) ∧ (156≦血糖値< 158) ∧ (精密検査=yes) 61 70 79 88 97 106 体重(kg) 各ピクセルの濃さはconfidenceを表す confidenceが大きいピクセルほど黒くなる support (88≦体重< 91) ∧ (156≦血糖値< 158) confidence: hit / support 25
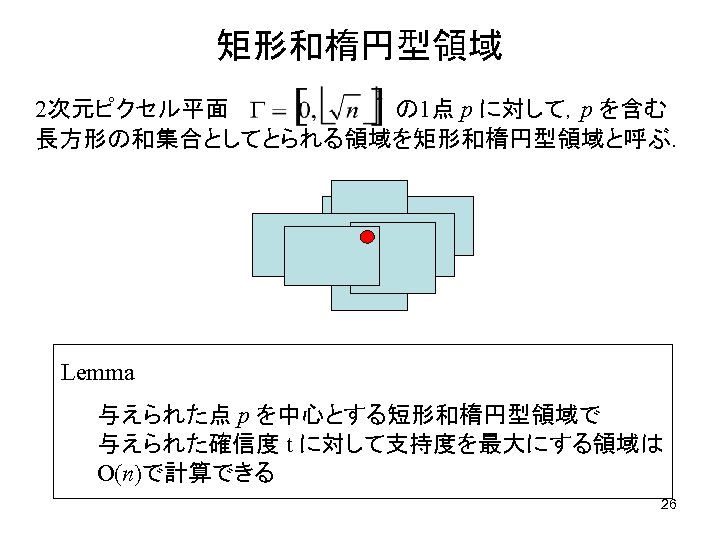
矩形和楕円型領域 2次元ピクセル平面 の 1点 p に対して,p を含む 長方形の和集合としてとられる領域を矩形和楕円型領域と呼ぶ. p Lemma 与えられた点 p を中心とする短形和楕円型領域で 与えられた確信度 t に対して支持度を最大にする領域は O(n)で計算できる 26
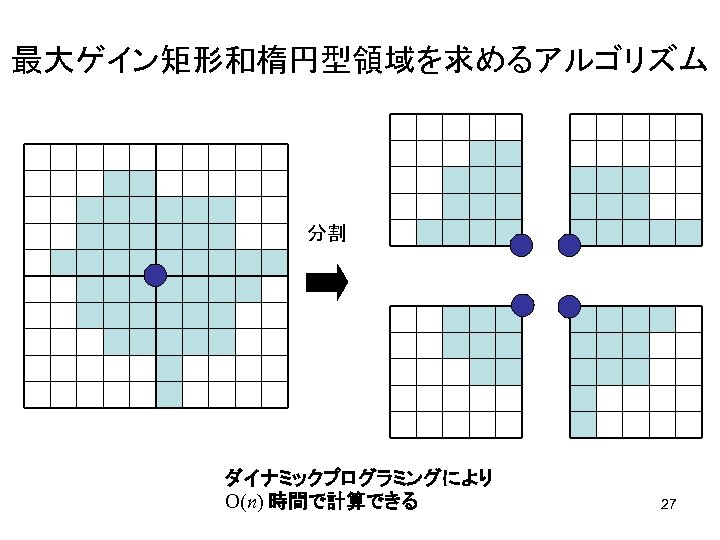
最大ゲイン矩形和楕円型領域を求めるアルゴリズム 分割 ダイナミックプログラミングにより O(n) 時間で計算できる 27
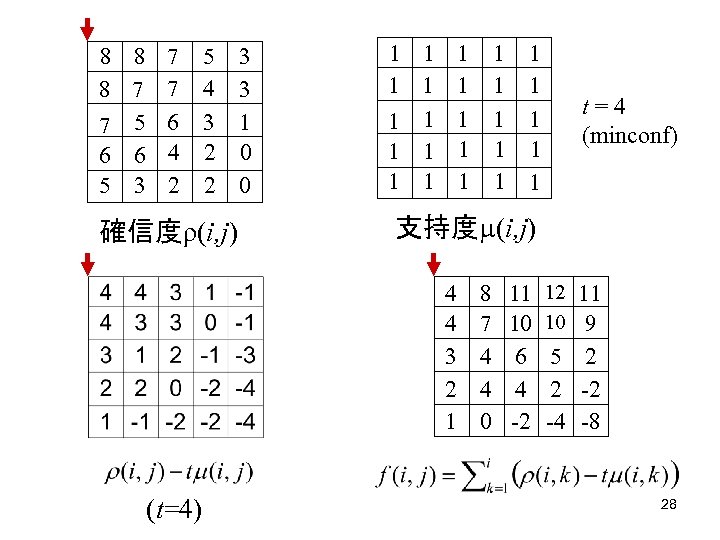
8 8 7 7 7 5 6 6 6 4 5 3 2 5 4 3 2 2 確信度ρ(i, j) 3 3 1 0 0 1 1 1 1 1 t=4 (minconf) 支持度 (i, j) 4 4 3 2 1 (t=4) 1 1 1 8 11 12 11 7 10 10 9 4 6 5 2 4 4 2 -2 0 -2 -4 -8 28
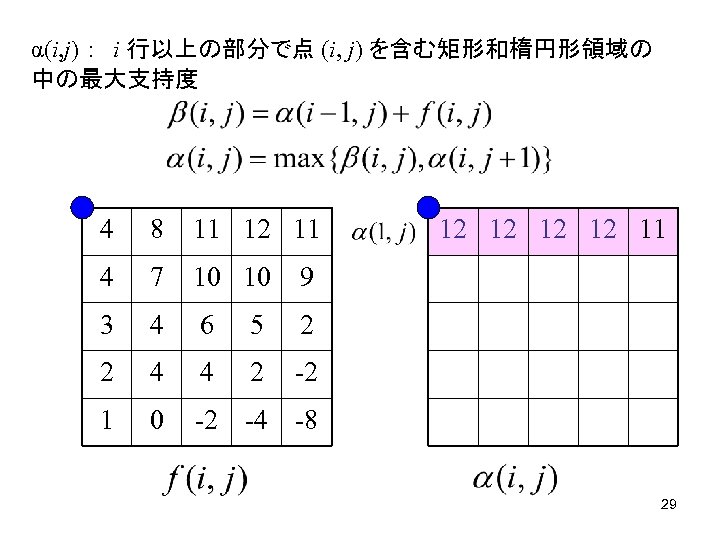
α(i, j) : i 行以上の部分で点 (i, j) を含む矩形和楕円形領域の 中の最大支持度 4 8 11 12 11 4 7 10 10 9 3 4 6 5 2 2 4 4 2 -2 1 0 12 12 11 -2 -4 -8 29
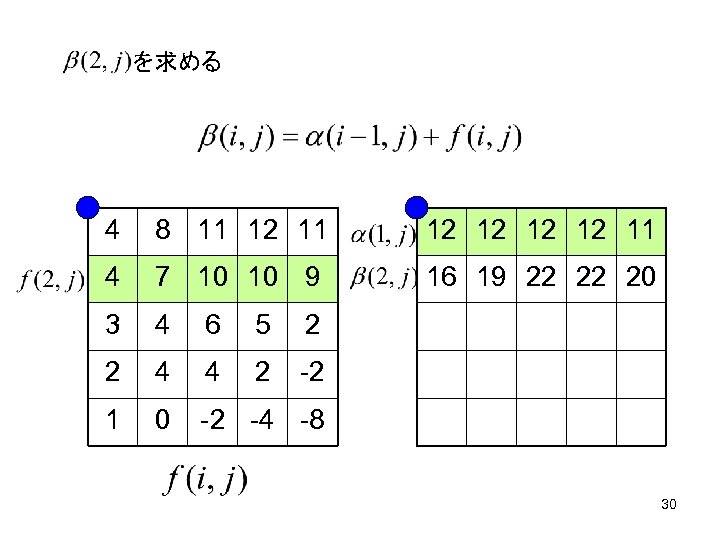
を求める 4 8 11 12 12 11 4 7 10 10 9 16 19 22 22 20 3 4 6 5 2 2 4 4 2 -2 1 0 -2 -4 -8 30
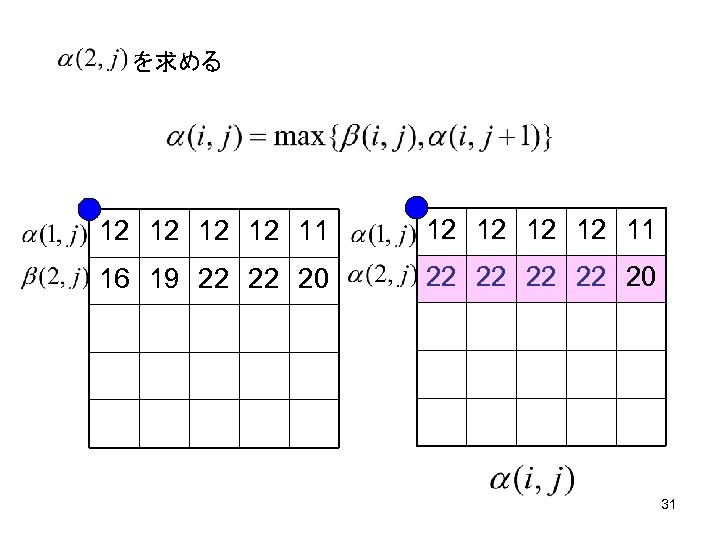
を求める 12 12 11 16 19 22 22 20 31
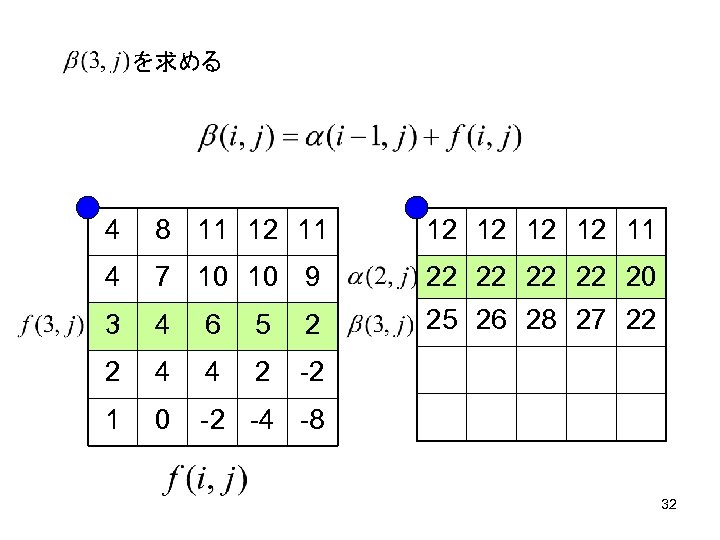
を求める 4 8 11 12 12 11 4 7 10 10 9 22 22 20 3 4 6 5 2 25 26 28 27 22 2 4 4 2 -2 1 0 -2 -4 -8 32
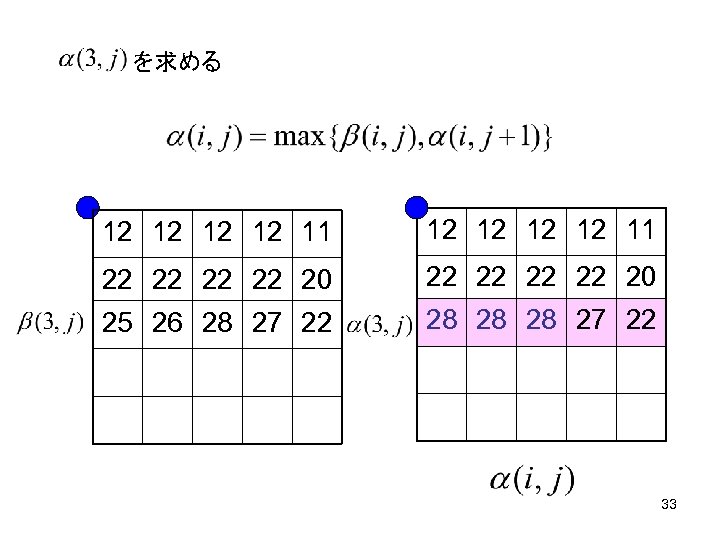
を求める 12 12 11 22 22 20 25 26 28 27 22 28 28 28 27 22 33
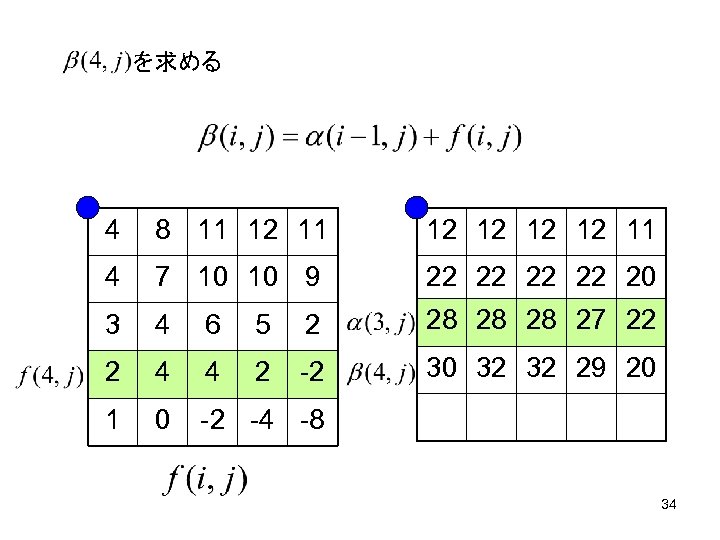
を求める 4 8 11 12 12 11 4 7 10 10 9 22 22 20 3 4 6 5 2 28 28 28 27 22 2 4 4 2 -2 30 32 32 29 20 1 0 -2 -4 -8 34
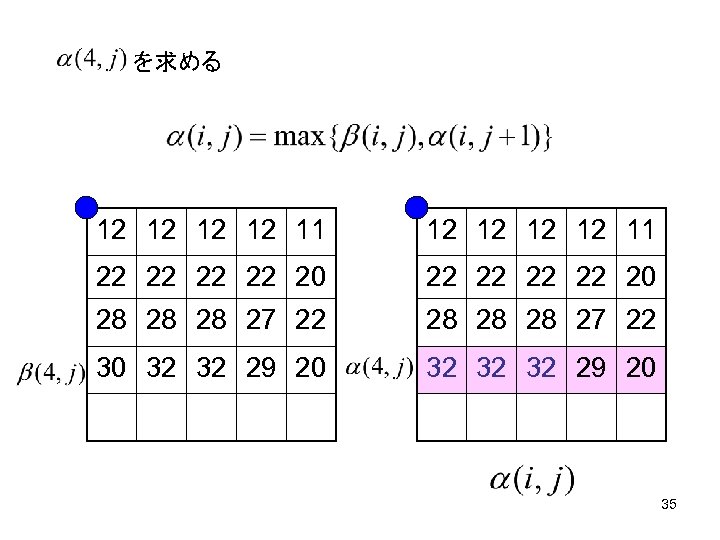
を求める 12 12 11 22 22 20 28 28 28 27 22 30 32 32 29 20 32 32 32 29 20 35
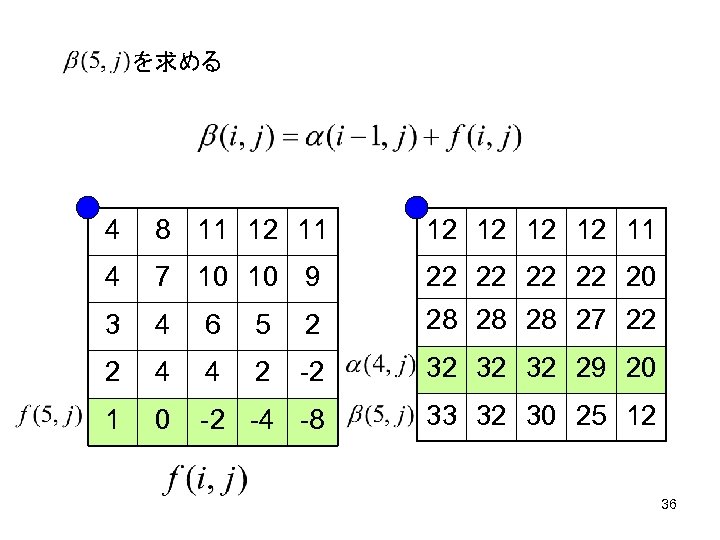
を求める 4 8 11 12 12 11 4 7 10 10 9 22 22 20 3 4 6 5 2 28 28 28 27 22 2 4 4 2 -2 32 32 32 29 20 1 0 -2 -4 -8 33 32 30 25 12 36

を求める 12 12 11 22 22 20 28 28 28 27 22 32 32 32 29 20 33 32 30 25 12 37
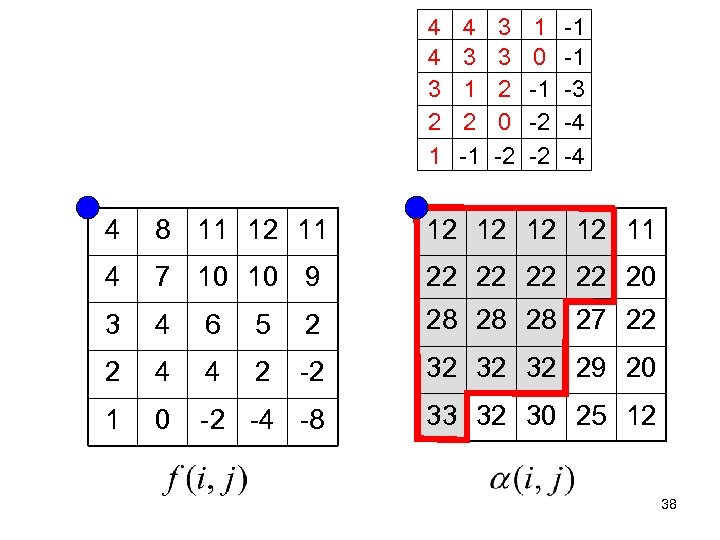
4 4 3 2 1 4 3 1 2 -1 3 3 2 0 -2 1 0 -1 -2 -2 -1 -1 -3 -4 -4 4 8 11 12 12 11 4 7 10 10 9 22 22 20 3 4 6 5 2 28 28 28 27 22 2 4 4 2 -2 32 32 32 29 20 1 0 -2 -4 -8 33 32 30 25 12 38

• ダイナミックプログラミングによりすべでのα( i , j )をO(n)時間で計算 • 最適領域のゲインは • 領域はダイナミックプログラミングのバックトラ ッキングにより計算 39
669871408ed2b1caf5015ace8d48f737.ppt