初中数学九年级上册 （苏科版） 5. 2 圆周角（二）
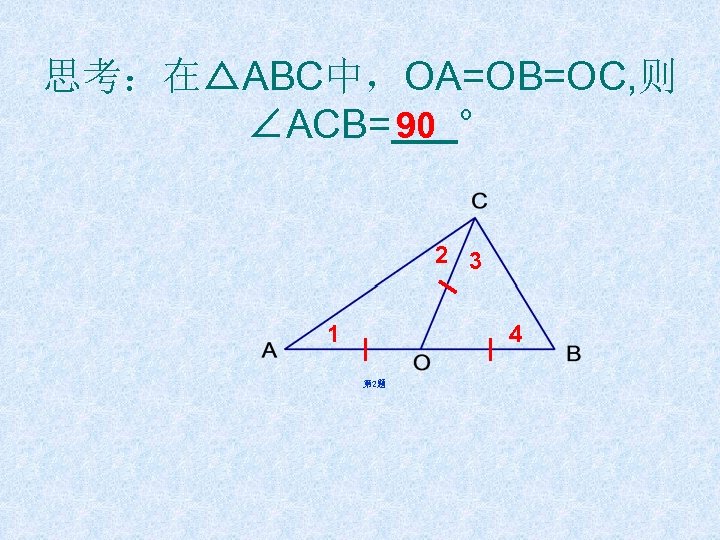
思考：在△ABC中，OA=OB=OC, 则 ∠ACB= 90 ° 2 3 1 4 第 2题
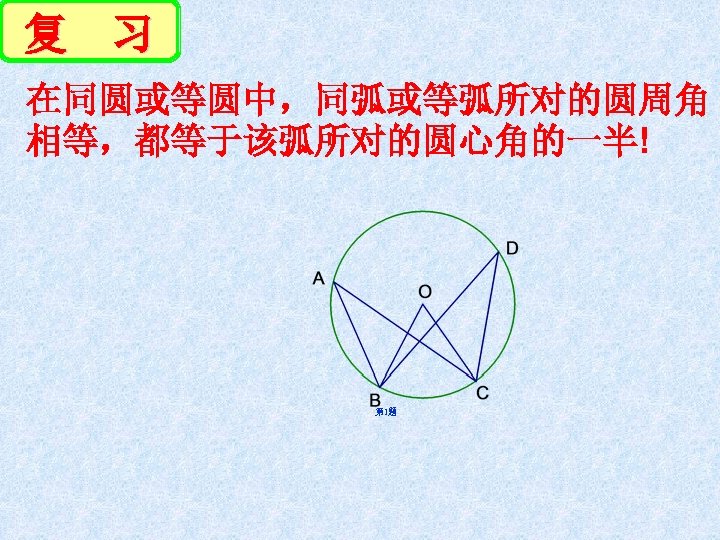
复 习 在同圆或等圆中，同弧或等弧所对的圆周角 相等，都等于该弧所对的圆心角的一半! 第 1题
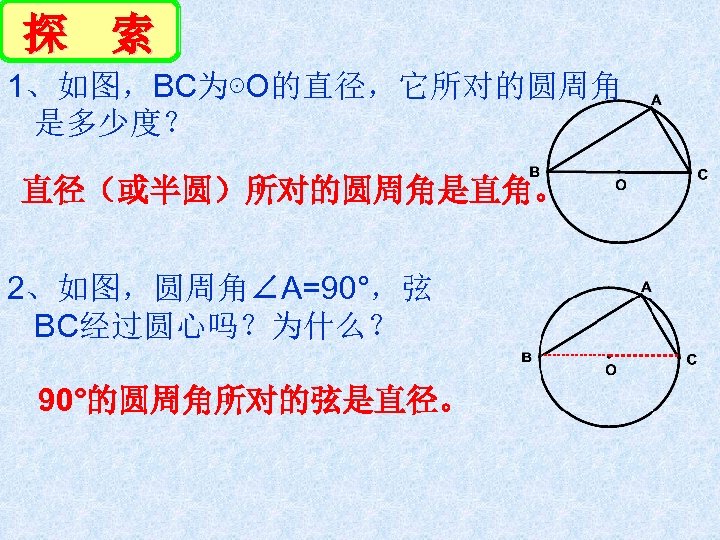
探 索 1、如图，BC为⊙O的直径，它所对的圆周角 是多少度？ 直径（或半圆）所对的圆周角是直角。 2、如图，圆周角∠A=90°，弦 BC经过圆心吗？为什么？ 90°的圆周角所对的弦是直径。
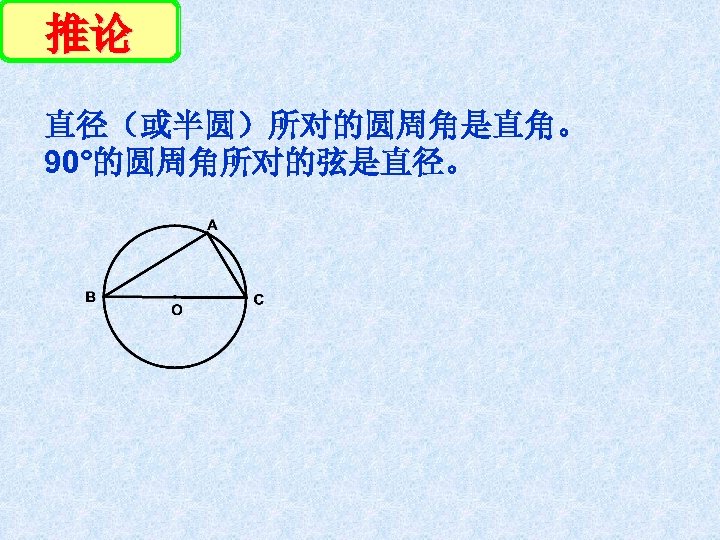
推论 直径（或半圆）所对的圆周角是直角。 90°的圆周角所对的弦是直径。
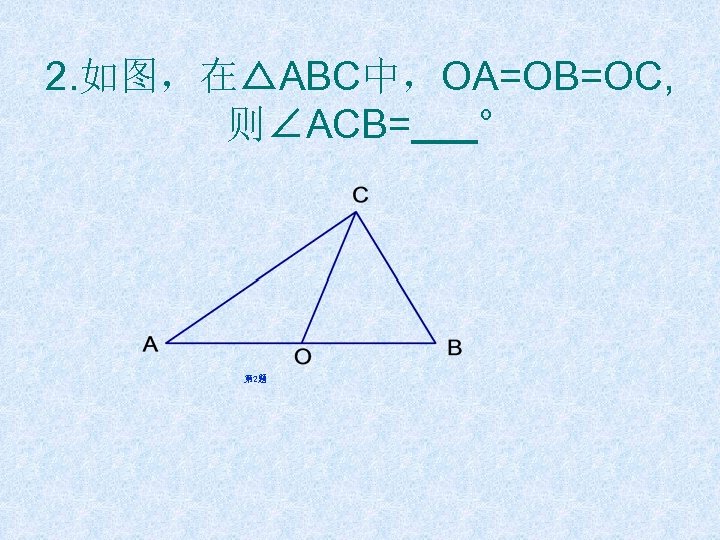
2. 如图，在△ABC中，OA=OB=OC, 则∠ACB= ° 第 2题
推论 直径（或半圆）所对的圆周角是直角。 90°的圆周角所对的弦是直径。
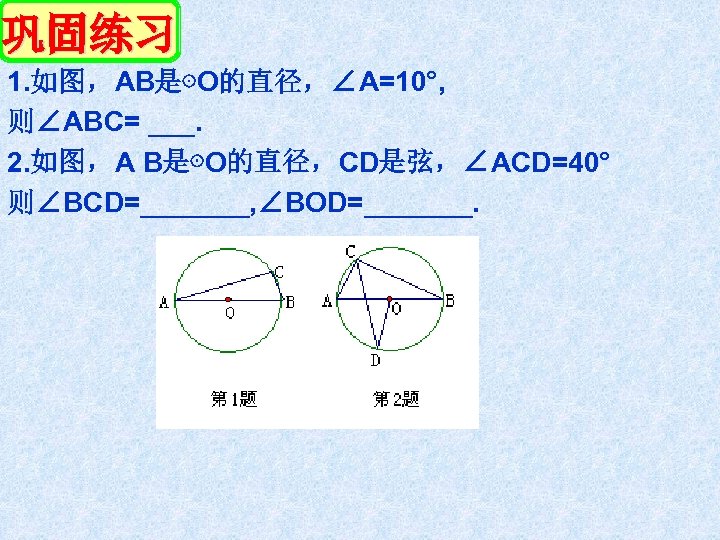
巩固练习 1. 如图，AB是⊙O的直径，∠A=10°, 则∠ABC= ___. 2. 如图，A B是⊙O的直径，CD是弦，∠ACD=40° 则∠BCD=_______, ∠BOD=_______.
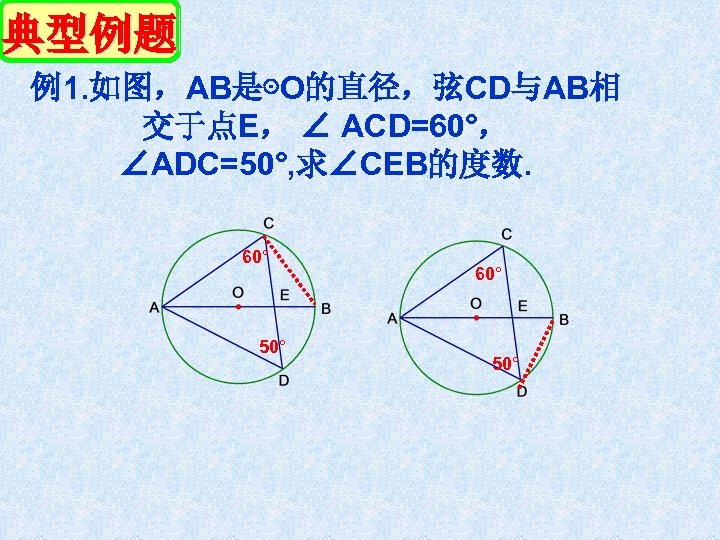
典型例题 例1. 如图，AB是⊙O的直径，弦CD与AB相 交于点E， ∠ ACD=60°， ∠ADC=50°, 求∠CEB的度数. 60° 50°
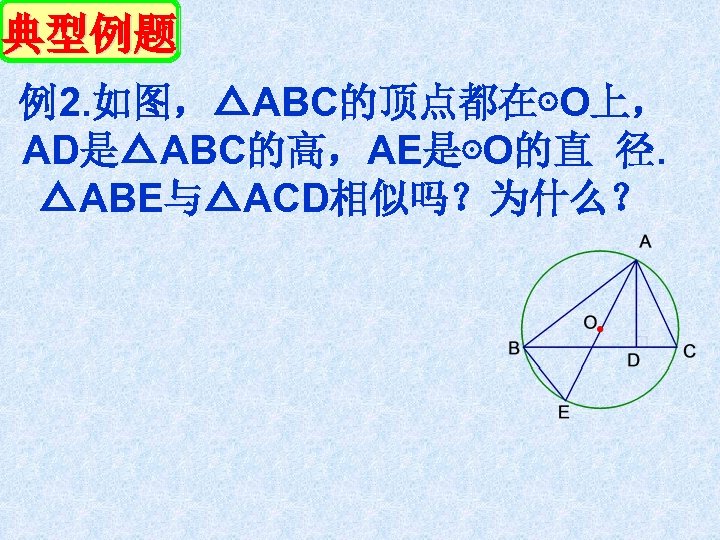
典型例题 例2. 如图，△ABC的顶点都在⊙O上， AD是△ABC的高，AE是⊙O的直 径. △ABE与△ACD相似吗？为什么？
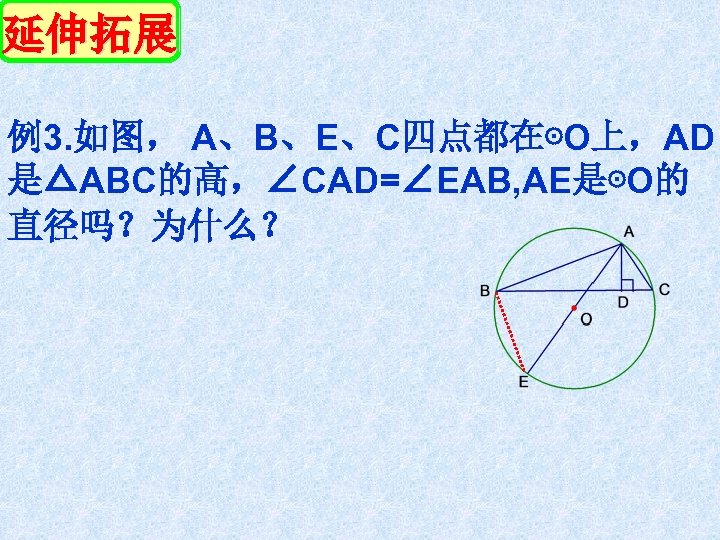
延伸拓展 例3. 如图， A、B、E、C四点都在⊙O上，AD 是△ABC的高，∠CAD=∠EAB, AE是⊙O的 直径吗？为什么？
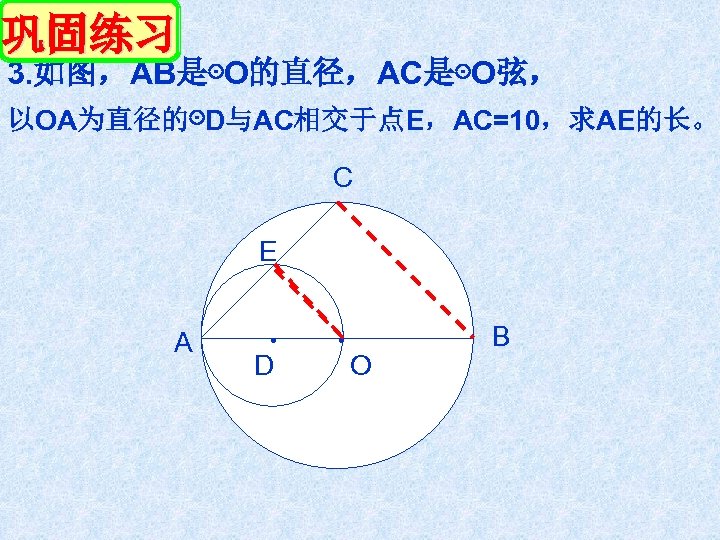
巩固练习 3. 如图，AB是⊙O的直径，AC是⊙O弦， 以OA为直径的⊙D与AC相交于点E，AC=10，求AE的长。 C E A ． ． D O B
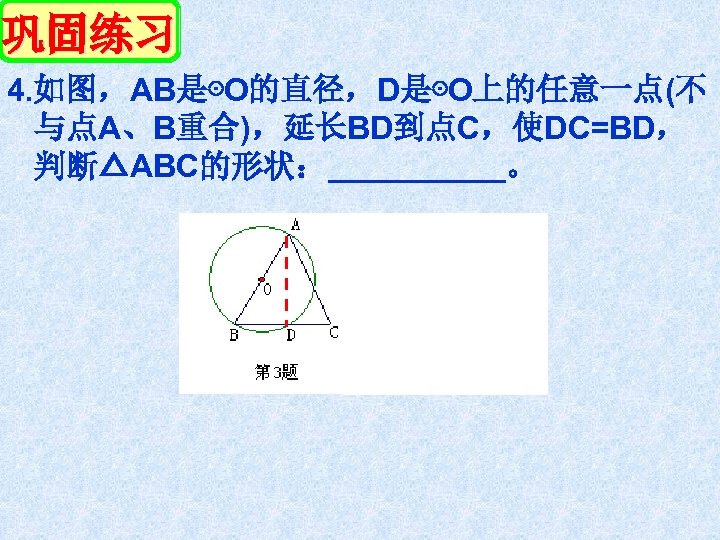
巩固练习 4. 如图，AB是⊙O的直径，D是⊙O上的任意一点(不 与点A、B重合)，延长BD到点C，使DC=BD， 判断△ABC的形状：_____。
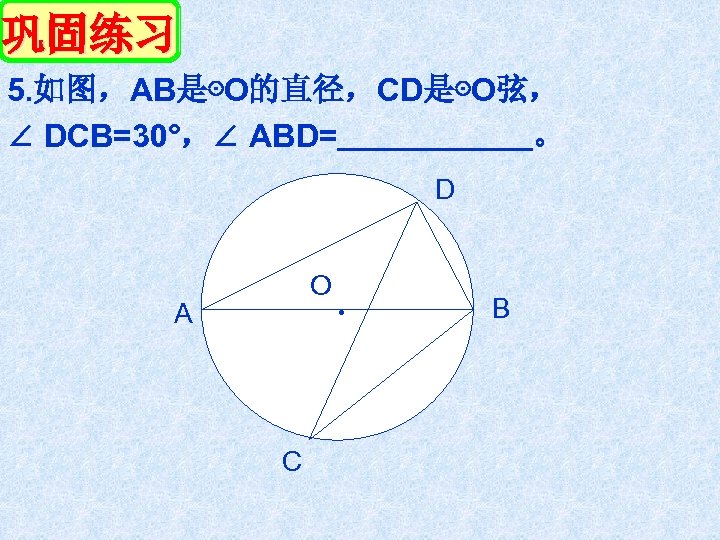
巩固练习 5. 如图，AB是⊙O的直径，CD是⊙O弦， ∠ DCB=30°，∠ ABD= 。 D O A C ． B
回顾总结 通过本课的学习，你又有 什么收获？
Скачать презентацию 初中数学九年级上册 苏科版 5 2 圆周角 二 思考 在 ABC中 OA OB OC 则
780b82feadbb8ca447c35c4f1cdc6a9f.ppt