スポーツスケジューリング問題 1993年Jリーグの再スケジューリング 文教大学 情報学部 経営情報学科 シミュレーション 2000年 11月24日

スポーツスケジューリング問題 ~1993年Jリーグの再スケジューリング~ 文教大学 情報学部 経営情報学科 「シミュレーション」 2000年 11月24日 東京大学 宮代 隆平

発表の概要 1993年Jリーグのスケジュールを 数理的手法を用いて改善 z スポーツスケジューリング問題とは？ z 1993年Jリーグのスケジュールと，その問題点 z 数理的手法によるスケジュールの改善過程＆結果 2

スポーツスケジューリング問題とは？ スポーツ競技（サッカー，バスケ，相撲，…）の “質の良い” スケジュールを作成する問題 → “良い（悪い）” スケジュールとは？ ・ 大相撲で，12日目に優勝力士が決まってしまう → 残りは消化取組になり，観客動員数減少 ・ ダイエー対巨人の日本シリーズ（7回戦） ただし，1～ 3戦が福岡，4～ 7戦が東京 → 不公平 3

スケジュール改善の例Ⅰ 5チームの総当りリーグ戦 チームＡ，Ｂが優勝候補とすると…（＊は休み） １ Ａ：Ｂ Ｂ：Ａ Ｃ：Ｅ Ｄ：＊ Ｅ：Ｃ ２ ＊ Ｃ Ｂ Ｅ Ｄ ３ Ｃ Ｄ Ａ Ｂ ＊ ４ Ｄ Ｅ ＊ Ａ Ｂ ５ １ ２ Ｅ Ａ：Ｅ Ｄ ＊ Ｂ：Ｄ ＊ Ｄ ⇒ Ｃ：＊ Ｅ Ｃ Ｄ：Ｂ Ａ Ａ Ｅ：Ａ Ｃ ３ ＊ Ｃ Ｂ Ｅ Ｄ ４ Ｃ Ｅ Ａ ＊ Ｂ ５ Ｂ Ａ Ｄ Ｃ ＊ 4

スケジュールに求められる要素 スケジュールを決定する時考慮すべき条件 試合の日時，競技場が使用可能か， 移動距離，本拠地 or 遠征，天気， ＴＶ放映，観客の満足度，チーム間の公平性， 各チームの強さ，… 最終目的は？ 費用削減，人気向上，興行収入増加，視聴率ｕｐ，… 5

スポーツスケジューリングの現状 現在，スポーツスケジューリングは ほとんど手作業で行われているのが現状 10チームの総当りリーグ戦の場合， 最低限の見積もりとして 9！（≒ 36万）通り以上のスケジュールが存在する → スケジューリングは適当でも良い？ 6

スポーツスケジューリングの重要性 ・ 移動距離減少をはかった問題では 手作業によるスケジュールと比較して 5～ 30％減少 ・ ある種のスポーツではスケジュールが試合結果に 大きな影響を与える → 悪いスケジュールでは競技自体の人気も下落 ・ 現在はＴＶ中継の時代（放映料，視聴率） 7

スケジュール改善の例Ⅱ 5チームによる総当りリーグ戦 ただし，コートが一つしかない → 特定のチームが連続して試合することを避ける １２３４５６７８９ 10 ＡＡＥＣＥＥＢＥＤＤ ⇒ ＣＢＡＢＡＢＤＡＣＡ ＢＣＤＤＡＣＣＢＢＡ ＤＥＣＤＥＣＥＢＥＤ 連戦が消失！ → 実は簡単？？ 8

スポーツスケジューリングの難しさ １２３４５６７８９ Ａ：Ｊ Ｆ Ｇ Ｃ Ｈ Ｂ Ｅ Ｂ：Ｉ Ｇ Ｄ Ｆ Ｅ Ａ Ｃ 10チームのリーグ戦 Ｃ：Ｈ Ｄ Ｅ Ａ Ｆ Ｇ Ｂ 6日目まで作成済み Ｄ：Ｇ Ｃ Ｂ Ｊ Ｉ Ｅ 7日目にＡ - Ｅ，Ｂ - Ｃの Ｅ：Ｆ Ｊ Ｃ Ｈ Ｂ Ｄ Ａ 対戦を組みたい Ｆ：Ｅ Ａ Ｉ Ｂ Ｃ Ｈ Ｇ：Ｄ Ｂ Ａ Ｉ Ｊ Ｃ Ｈ：Ｃ Ｉ Ｊ Ｅ Ａ Ｆ Ｉ：Ｂ Ｈ Ｆ Ｇ Ｄ Ｊ Ｊ：Ａ Ｅ Ｈ Ｄ Ｇ Ｉ 9

スポーツスケジューリングの難しさ １２３４５６７８９ Ａ：Ｊ Ｆ Ｇ Ｃ Ｈ Ｂ Ｅ Ｂ：Ｉ Ｇ Ｄ Ｆ Ｅ Ａ Ｃ 10チームのリーグ戦 Ｃ：Ｈ Ｄ Ｅ Ａ Ｆ Ｇ Ｂ 6日目まで作成済み Ｄ：Ｇ Ｃ Ｂ Ｊ Ｉ Ｅ Ｆ 7日目にＡ - Ｅ，Ｂ - Ｃの Ｅ：Ｆ Ｊ Ｃ Ｈ Ｂ Ｄ Ａ 対戦を組みたい Ｆ：Ｅ Ａ Ｉ Ｂ Ｃ Ｈ Ｄ Ｇ：Ｄ Ｂ Ａ Ｉ Ｊ Ｃ Ｈ：Ｃ Ｉ Ｊ Ｅ Ａ Ｆ Ｉ：Ｂ Ｈ Ｆ Ｇ Ｄ Ｊ Ｊ：Ａ Ｅ Ｈ Ｄ Ｇ Ｉ 10

スポーツスケジューリングの難しさ １２３４５６７８９ Ａ：Ｊ Ｆ Ｇ Ｃ Ｈ Ｂ Ｅ Ｂ：Ｉ Ｇ Ｄ Ｆ Ｅ Ａ Ｃ 10チームのリーグ戦 Ｃ：Ｈ Ｄ Ｅ Ａ Ｆ Ｇ Ｂ 6日目まで作成済み Ｄ：Ｇ Ｃ Ｂ Ｊ Ｉ Ｅ Ｆ 7日目にＡ - Ｅ，Ｂ - Ｃの Ｅ：Ｆ Ｊ Ｃ Ｈ Ｂ Ｄ Ａ 対戦を組みたい Ｆ：Ｅ Ａ Ｉ Ｂ Ｃ Ｈ Ｄ Ｇ：Ｄ Ｂ Ａ Ｉ Ｊ Ｃ Ｈ Ｈ：Ｃ Ｉ Ｊ Ｅ Ａ Ｆ Ｇ Ｉ：Ｂ Ｈ Ｆ Ｇ Ｄ Ｊ Ｊ：Ａ Ｅ Ｈ Ｄ Ｇ Ｉ 11

スポーツスケジューリングの難しさ １２３４５６７８９ Ａ：Ｊ Ｆ Ｇ Ｃ Ｈ Ｂ Ｅ Ｂ：Ｉ Ｇ Ｄ Ｆ Ｅ Ａ Ｃ 10チームのリーグ戦 Ｃ：Ｈ Ｄ Ｅ Ａ Ｆ Ｇ Ｂ 6日目まで作成済み Ｄ：Ｇ Ｃ Ｂ Ｊ Ｉ Ｅ Ｆ 7日目にＡ - Ｅ，Ｂ - Ｃの Ｅ：Ｆ Ｊ Ｃ Ｈ Ｂ Ｄ Ａ 対戦を組みたい Ｆ：Ｅ Ａ Ｉ Ｂ Ｃ Ｈ Ｄ Ｇ：Ｄ Ｂ Ａ Ｉ Ｊ Ｃ Ｈ Ｈ：Ｃ Ｉ Ｊ Ｅ Ａ Ｆ Ｇ Ｉ：Ｂ Ｈ Ｆ Ｇ Ｄ Ｊ Ｊ ← 既に対戦済！ Ｊ：Ａ Ｅ Ｈ Ｄ Ｇ Ｉ Ｉ 12

スポーツスケジューリングの難しさ １２３４５６７８９ Ａ：Ｊ Ｆ Ｇ Ｃ Ｈ Ｂ Ｅ Ｂ：Ｉ Ｇ Ｄ Ｆ Ｅ Ａ ↓ 7日目にＡ - Ｅの対戦 Ｃ：Ｈ Ｄ Ｅ Ａ Ｆ Ｇ Ｉ ↓ Ｄ：Ｇ Ｃ Ｂ Ｊ Ｉ Ｅ Ｃの相手は Ｉ のみ Ｅ：Ｆ Ｊ Ｃ Ｈ Ｂ Ｄ （Ｂ ｰ Ｃは不可能） Ｆ：Ｅ Ａ Ｉ Ｂ Ｃ Ｈ Ｇ：Ｄ Ｂ Ａ Ｉ Ｊ Ｃ 人間の目で判断するのは Ｈ：Ｃ Ｉ Ｊ Ｅ Ａ Ｆ 非常に難しい！ Ｉ：Ｂ Ｈ Ｆ Ｇ Ｄ Ｊ Ｊ：Ａ Ｅ Ｈ Ｄ Ｇ Ｉ 13

手作業での問題点 手作業では… ・ 全てのスケジュールを考慮するのは無理！ ・ 本当に最適？公平？ ・ この条件下でスケジュールが作成可能？ ・ 作成時間，各方面との調整，…（Jリーグは半年程度） ・ 予定していた日に競技場が使えなくなった！ → 数理的手法の必要性 14

数理的手法の必要性 数理的手法を用いれば… ・ 制約を満たすスケジュールが短時間で作成可能 ・ 公平性，最適性が明らか ・ 最適化問題としてモデル化することにより， 条件の変化にも容易に対応可能 → 1993年Jリーグのスケジュールへ 15

1993年Jリーグの概略 Jリーグ開幕の年，サッカーブーム 10チームによる二重総当りリーグ戦 （後述） 第 1節は土曜日，以降水曜日，土曜日，…（全 18節） 5月15日（土）～ 7月14日（水） チーム略号 Ｋ：鹿島アントラーズ，Ｖ：ヴェルディ川崎， Ｍ：横浜マリノス，Ｅ：清水エスパルス，Ｊ：ジェフ市原， Ｓ：サンフレッチェ広島，Ｆ：横浜フリューゲルス，Ｇ：ガンバ大阪， Ｎ：名古屋グランパス， Ｒ：浦和レッズ 16

1993年Jリーグのスケジュール 17

二重総当りリーグ戦 18

ミラーリング 19

1993年スケジュールのミラーリング １９９３年Jリーグのスケジュールにおいて， ミラーリングの対応関係は （1，11），（2，10），（3，18），（4，12），（5，13）， （6，14），（7，15），（8，16），（9，17） → 理由は不明だが，最小対戦間隔は 十分に開いている（中 7節） 20

1993年Jリーグのスケジュール 21

1993年スケジュールの分析 本拠地での試合をｈ （ホーム） 遠征先での試合をａ （アウェイ）と表記 10チームの二重総当りリーグ戦ではｈ，ａが9回ずつ ・ 各チームとも土曜日に 4または 5個のｈ （土曜日は観客動員数が水曜日の 1. 3倍） ・ 各チームとも前半（第 1～ 9節）までに 4または 5個のｈ → この二点に関しては公平 22

1993年スケジュールの問題点 一般にａの連続は嫌われる → スケジュール中，チームＫの第 9，10，11節のみ ａが3連続！（他チームにはない） 公平性？ また，土曜日のスケジュールのみを抜き出すと… → 観客にとって親切でない！ 23

1993年Jリーグのスケジュール 24

土曜日だけ着目すると… 25

1993年スケジュールの問題点 ・ チームＫのみ，3連続ａがある ・ 土曜日（水曜日）のみを考えると， いくつかのチームに関して 本拠地での試合間隔が開きすぎ ・ 他にも様々な問題点 （本拠地が同一のＭとＦを考慮していない，…） → 数理的手法を用いて改善を試みる！ 26

全列挙法 全列挙して，最適なスケジュールを選択？ → 10チームの二重総当りリーグ戦 最低限のスケジュール総数は 18！（≒ 6400兆） 1秒間に 1億個のスケジュールが作れる 仮想計算機で 2年 ただ計算機を用いてもダメ！ → 当時論文で提案されていた方法を改良して使用 27

数理的手法の参考文献 G. L. Nemhauser and M. A. Trick, “Scheduling a Major College Basketball Conference, ” Operations Research, 46(1998), 1‐ 8. 実際に，米の大学バスケ対抗戦（9チーム）の スケジューリングを行った論文 → 数理的手法の説明 28

スケジュール 29

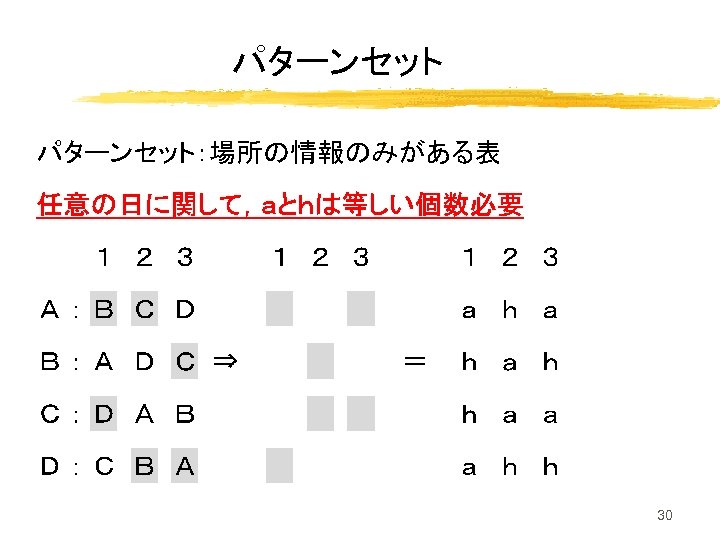
パターンセット 30

パターンセットの横一行だけを取り出した文字列 ａａａ，ａａｈ，ａｈａ，ａｈｈ，ｈａａ，ｈａｈ，ｈｈａ，ｈｈｈ それぞれのチームはこの文字列通り移動する パターン → パターンセット → スケジュール → 最適解 ↑ ↑ ↑ 制約条件 31

スケジュール作成までの流れ 32

パターンセット → スケジュール 一般に，1つのパターンセットからは… ・ 多数のスケジュールが生成される ・ スケジュールが全く生成できない → 不可能な例 １ ２ ３ ４ ５ （6チーム） ａ ｈ ｈ ａ ｈ ａ ａ ｈ 与えられたパターンセットに， ａ ｈ ｈ 各チームを割り当てることが可能 ？ ｈ ａ ａ ｈ ａ （＝スケジュールを生成） ｈ ａ ｈ ｈ ａ → 整数計画問題として定式化 ｈ ａ ａ 33

整数計画問題としての定式化 １２３ α：ｈ ａ ｈ = 1 ： α→γが2日目に対戦する β：ｈ ａ ａ = 0 ： α→γが2日目に対戦しない γ：ａ ｈ ｈ 対戦可能な変数のみを定義 δ：ａ ｈ ａ 全ての変数は 0 - 1整数変数 基本的な制約条件 （βとγが必ず 1回対戦） （αは 3日目に必ず 1試合行う） 34

整数計画問題の例 x 121+x 141+x 321+x 341+x 212+x 242+x 312+x 342+x 213+x 233+x 413+x 433=6, x 121+x 212+x 213=1, x 312=1, x 141+x 413=1, x 321+x 233=1, x 242=1, x 341+x 342+x 433=1, １２３ x 121+x 141=1, x 212+x 312=1, x 213+x 413=1, １：ａ ｈ ｈ x 121+x 321=1, x 212+x 242=1, x 213+x 233=1, ２：ｈ ａ ａ x 321+x 341=1, x 312+x 342=1, x 233+x 433=1, ３：ａ ａ ｈ x 141+x 341=1, x 242+x 342=1, x 413+x 433=1, ４：ｈ ｈ ａ ∀x∈｛ 0, 1｝. （x の添え字はａ，ｈ，日の順） 35

整数計画問題について 定式化した整数計画問題（今回の場合，225変数）は ソフトウェアに解かせる 問題に解がある ＝ パターンセットにチーム割当可能 問題が不能 ＝ パターンセットにチーム割当不可能 制約条件が少ないと時間がかかり，また多数の解 制約条件が多すぎると矛盾することが多い 36

スケジュールの作成 元のスケジュールより良いものを作りたい！ 問題点の復習 ・ チームＫのみ，3連続ａがある ・ 土曜日を考えると，いくつかのチームに関し 本拠地での試合間隔が開きすぎ ・ 他にも様々な問題点 （本拠地が同一のＭとＦを考慮していない，…） 37

前提条件 ・ 元のスケジュールより劣ったものは作らない（目標） ・ （変則的な）ミラーリングは同じとする ・ 開幕戦（第 1節）と最終戦（第 18節，第 3節に対応）は 元のスケジュールと全く同じにする → スケジュール作成の実験開始 38

パターン生成 1993年はチーム数が10→ パターンの長さは 9 ａａａａａ，ａａａａｈ，…，ｈｈｈｈｈ（512個） ・ 3連続ａ，3連続ｈはだめ ・ 土曜日には 4または 5個のｈ ・ 前半戦に 4または 5個のｈ ・ 土曜（水曜）だけ注目したとき，3連続ａ（ｈ）はだめ → 24個のパターンが残った 39

24個の許容パターン ａａｈｈａ， ａａｈｈａｈｈａａ， ａｈａａｈａａｈｈ， ａｈａａｈａｈｈａ， ａｈａａｈｈａａｈ， ａｈａａｈｈａｈａ， ａｈａｈｈａｈｈａ， ａｈａｈｈａａｈｈ， ｈａａｈａａｈｈａ， ｈａａｈａｈｈａｈ， ｈａｈａａｈａａｈ， ｈａｈａａｈｈａａ， ｈａｈａａｈｈａｈ， ｈａｈｈａａｈａａ， ｈａｈｈａａｈａｈ， ｈａｈｈａ， ｈａｈｈａｈａａｈ， ｈａｈｈａｈｈａａ， ｈｈａａｈａａｈｈ， ｈｈａａｈ 40

パターンからパターンセットへ 24個のパターンを 10個組み合わせて， パターンセットを作る → 24Ｃ 10≒ 200万 その中で，任意の日についてａとｈが等しい必要有り ａａｈ ａｈｈ → 200万個中，1382個が合格 ｈａｈ （計算時間 5分） ｈｈａ ↑対戦不可能！ 41

思考錯誤 パターンセット1382個は候補が多すぎる！ 「第 1, 2節，第 17, 18節にａａを禁止」 （旧スケジュールは合計2チーム） パターンセットがただ 1個に！！ しかし，スケジュール割当て不可能であった… → （やり直し） 42

パターンセットを減らす パターンセット1382個のうち， 実際に（1つ以上の）スケジュールを生成できるもの？ 整数計画問題に定式化して判定（1382問） → 208個が合格（計算時間約30分） 1つのパターンセットからは， 多数のスケジュールが生成可能．（まだまだ多い） 43

条件の適用 「第 1, 2節，第 17, 18節のａａをできるだけ避ける」 （旧スケジュールは合計2チーム） この条件を適用すると…，パターンセットが7個に！ 参考文献ではこの段階で 17個 → 24時間 計算時間の見積り 24＊10＊7／ 17 ＝ 100時間 まだパターンセットが多い！（ここでしばらく挫折） 44

新たな制約条件の導入 チームＭとチームＦは本拠地が同一 ☆同時にホームゲームは戦えない！ 正反対のパターンが必要 （例） チームＭ：ａｈａａｈ チームＦ：ｈａｈｈａ → さらに，ＭとＦが対戦する日を考える 45

Ｍ－Ｆ条件の導入 チームＭ：ａｈａａｈ チームＦ：ｈａｈｈａ チームＭ，Ｆが上のパターンである時， ＭとＦが戦えるのは？（本拠地は同一） → 本拠地が3連続しないことを考えると チームＭ：ａｈａａｈｈａ チームＦ：ｈａｈｈａａｈ Ｆ ｈ 対戦可能なのは Ｍａ ← ここだけ！ 46

パターンセットの決定 ・ Ｍ－Ｆ条件 ・ 第 1節と第 18節を旧スケジュールと同一にする 以上の条件を考慮した結果， パターンセットは（運良く）1個に！ さらに，いくつかの試合が固定された → ここまでの状況 47

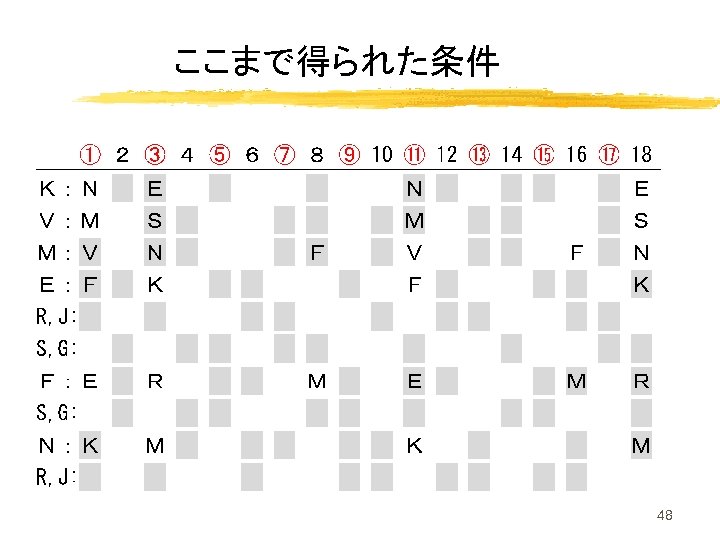
ここまで得られた条件 48

さらなる 夫 前頁のパターンセットを整数計画問題として， 全ての解（＝スケジュール）を求めると… → 時間がかかりすぎていつ終わるか不明 チームＲ，Ｊ，Ｓ，Ｇの割り当ては 4通り → 割り当てたスケジュールを解く！ （子問題に分割） 49

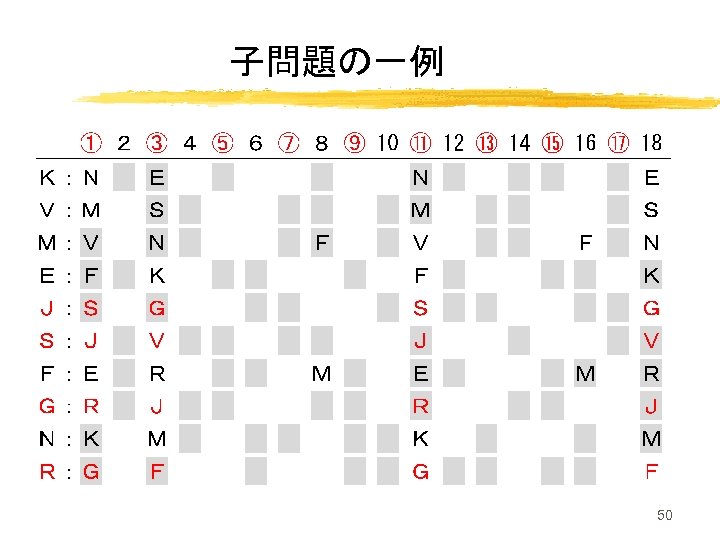
子問題の一例 50

子問題に分割して解く チームＲ，Ｊ，Ｓ，Ｇを割り当て， 4つの整数計画問題に分割して解くと… → 問題Ⅰ 18個 6分 問題Ⅱ 22個 7分 問題Ⅲ 14個 2分 問題Ⅳ 18個 4分 合計 72個 20分 分割しないと，同じ 72個を 得るのに 56時間を要した！ 51

最終スケジュールの選択 得られた 72個のスケジュール中， 少数のスケジュールを選択したい！ → 強豪チームとの連続対戦に注目 旧スケジュールでは 8箇所 ただ 1個のスケジュールが，8箇所未満（7）であった！ → スケジュールの紹介 52

新たに提案するスケジュール 53

新スケジュール（土曜日のみ） 54

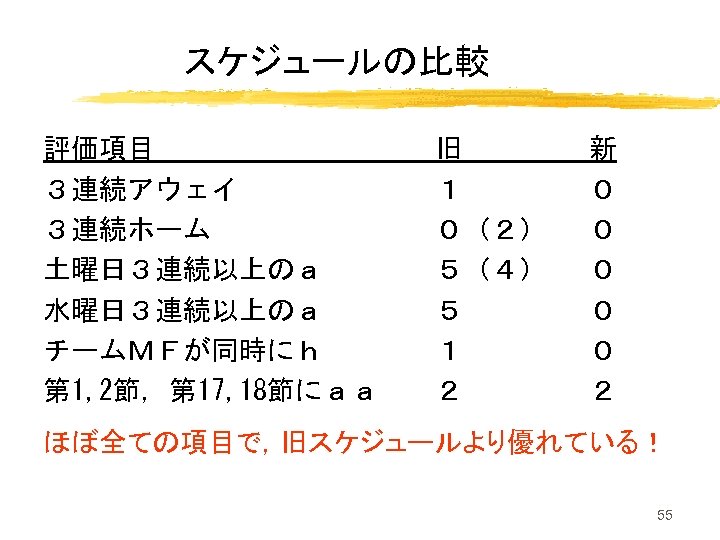
スケジュールの比較 評価項目 ３連続アウェイ ３連続ホーム 土曜日３連続以上のａ 水曜日３連続以上のａ チームＭＦが同時にｈ 第 1, 2節，第 17, 18節にａａ 旧 １ ０（２） ５（４） ５ １ ２ 新 ０ ０ ０ ２ ほぼ全ての項目で，旧スケジュールより優れている！ 55

スケジュール計算過程 全パターン → パターンセット 512個 24個 （5分） 1382個 → スケジュール生成可能ＰＳ → 選択されたＰＳ （30分） 208個 7個 → 1個 最終ＰＳ → スケジュール → 最終スケジュール 1個 （20分） 72個 1個 56

問題点 ・ 現在はもっとチーム数が多い（16チーム） → 制約条件によっては可能 ・ 第 1節と第 18節を同じにすることの妥当性 → ＴＶ中継，企業秘密… ・ 解法全体として，場当たり的（Ｍ－Ｆ条件など） → 一般的なアルゴリズムの必要性 57

まとめ スポーツスケジューリング問題について概説し， 問題の重要性，数理的取り扱いの必要性を示した． 1993年Jリーグのスケジュールの問題点を指摘し， 数理的手法による再スケジューリングを行った． 提案する新スケジュールは，旧スケジュールにおける 問題点が全て改善されている． 58

参考文献 Webページ http: //www. misojiro. t. u-tokyo. ac. jp/~tomomi/sportsscheduling. html 日本語の解説記事 松井知己, 「スポーツのスケジューリング」, オペレーションズリサーチ，44 (1999), 141－146. 宮代隆平, 松井知己, 「1993年Jリーグの再スケジューリング」, オペレーションズ・リサーチ, 45 (2000), 81－83. お問い合わせは [email protected]. t. u-tokyo. ac. jp まで 59