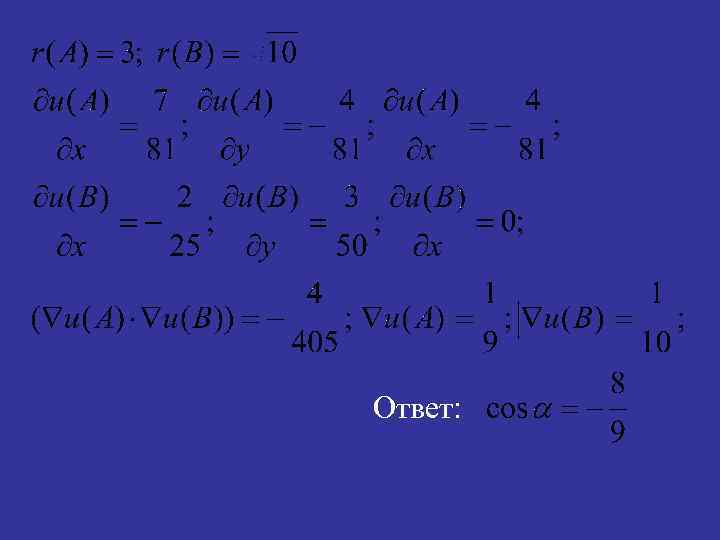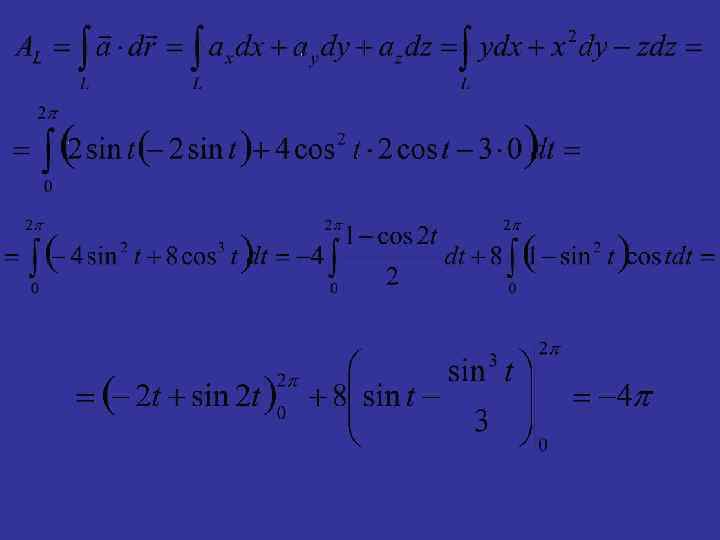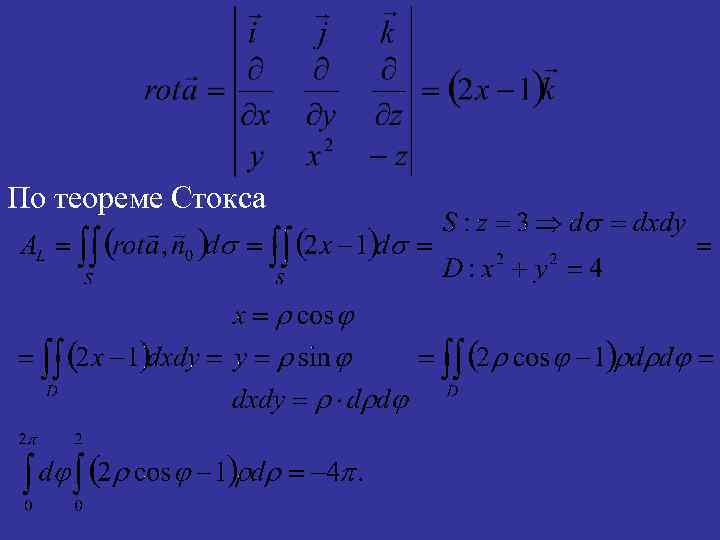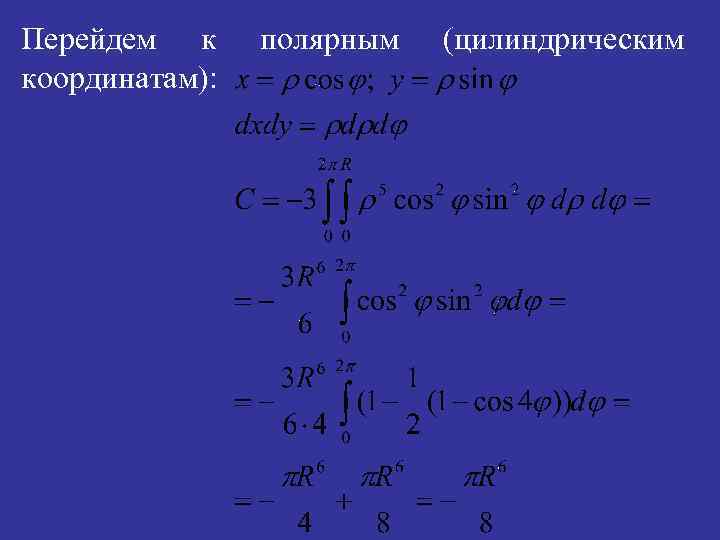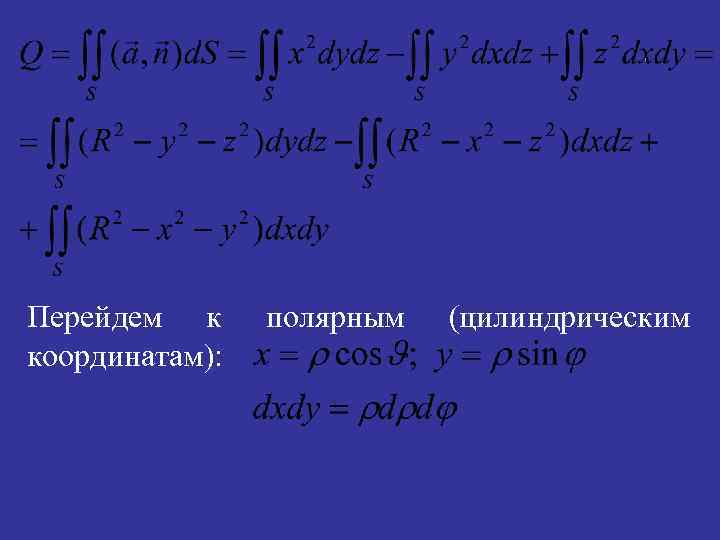Задача 1 Найти градиент скалярного поля в точке

Задача 1. Найти градиент скалярного поля в точке М(2, 1). Решение. Ответ:

Задача 2. Найти косинус угла a между градиентами поля в точках А(1, 2, 2) и В(-3, 1, 0). Решение.

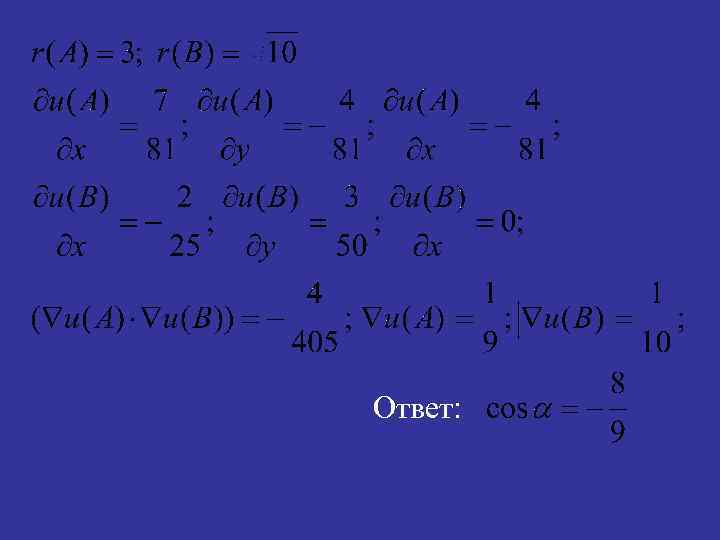Ответ:

Задача 3. Для функции найти производную по направлению внутренней нормали к цилиндрической поверхности x 2 + z 2 = a 2 + c 2 в точке M 0(a, b, c). Решение. Пусть f(x, y, z) = x 2 + z 2. Данная в условии поверхность – это поверхность уровня для f, проходящая через точку M 0. Имеем Функция f в точке M 0 растет быстрее всего по направлению grad f, значит, по направлению нормали к заданной поверхности.

Исходя из вида функции f, заключаем, что это – направление внешней нормали. Следовательно, единичный вектор внутренней нормали в точке M 0 будет равен

Ответ:

Задача 4. Найти дивергенцию векторного поля: Решение. Ответ:

Задача 5. Вычислить поток векторного поля a = (z 2 – x, 1, y 5) через внутреннюю поверхность S: y 2 = 2 x, отсеченную плоскостями: x = 2, z = 0, z = 3. Решение.

Задача 6. Найти ротор векторного поля: Решение.

Задача 6. Найти циркуляцию вектора по контуру непосредственно и по формуле Стокса. z n y x

Решение. I способ Контур L - окружность радиуса R, лежащая в плоскости z = 3. Выберем ориентацию как показано на рисунке, т. е. против часовой стрелки. Параметрические уравнения окружности имеют вид

II способ. Для вычисления циркуляции по теореме Стокса выберем какую-нибудь поверхность S, натянутую на контур. Естественно в качестве S взять круг, имеющий контур L своей границей. Уравнение поверхности S имеет вид: Согласно выбранной ориентации контура нормаль к поверхности необходимо взять равной

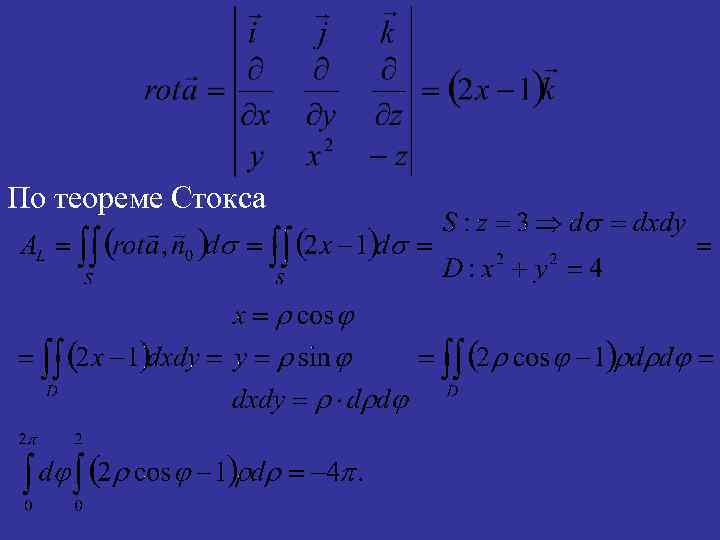По теореме Стокса

Задача 7. С помощью теоремы Стокса найти циркуляцию векторного поля По сечению x 2 + y 2 + z 2 = R 2 плоскостью z = 0. Решение. По формуле Стокса

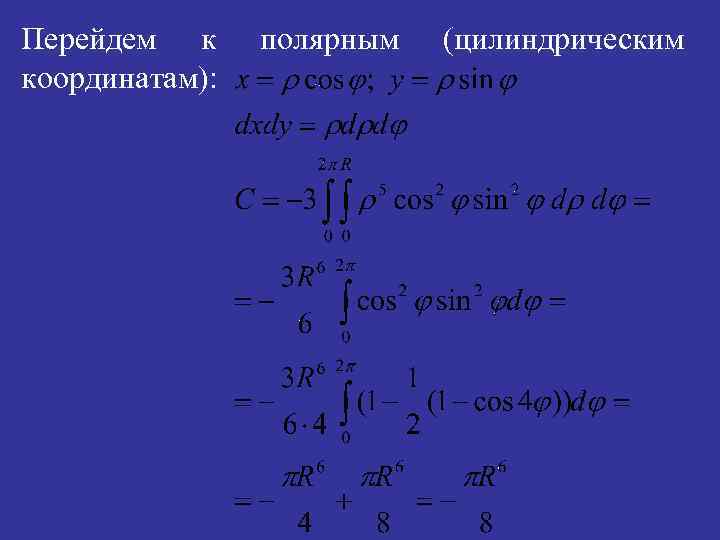Перейдем к координатам): полярным (цилиндрическим

Задача 8. Найти поток вектора через часть сферы x 2 + y 2 + z 2 = R 2 , при x ≥ 0, y ≥ 0, z ≥ 0, в направлении внешней нормали. Решение. По определению потока вектора через поверхность, находим

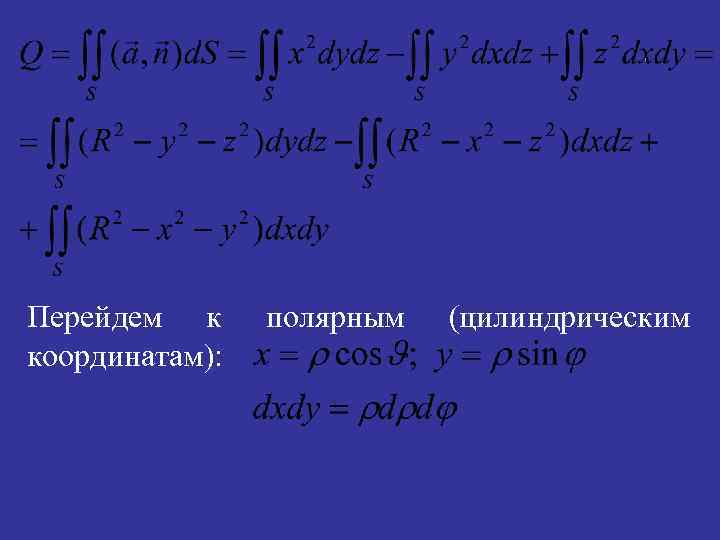Перейдем к координатам): полярным (цилиндрическим

Задача 9. Пользуясь формулой Остроградского. Гаусса вычислить интеграл где S – внешняя сторона сферы Решение. По формуле Остроградского-Гаусса

Перейдем к сферическим координатам: Якобиан перехода имеет вид: Ответ: