@ Я. Притула 1 Основні ймовірнісні розподіли













- Размер: 154.5 Кб
- Количество слайдов: 14
Описание презентации @ Я. Притула 1 Основні ймовірнісні розподіли по слайдам
 @ Я. Притула 1 Основні ймовірнісні розподіли
@ Я. Притула 1 Основні ймовірнісні розподіли
 @ Я. Притул а 2 Біноміальний розподіл Якщо випадкова величина приймає лише два значення (тобто або подія настає з ймовірністю р , або не настає з ймовірністю (1 -р) ) і повторюється n р азів, то випадкова величина Х, що рівна кількості разів настання подій має біноміальний розподіл. Важливим є незалежність послідовності повторів. Мат. сподівання біноміального розподілу = p * n Стандартне відхилення біноміального розподілу = Ймовірність того, що при n спробах буде рівно k успіхів: В Excel: =БИНОМРАСП чи = BINOMDIST , формально де)1(pnp knkn kpp. Ck. XP )1()( ))(. . . 21(). . . 21(. . . 21 )!(! ! knk n C n k
@ Я. Притул а 2 Біноміальний розподіл Якщо випадкова величина приймає лише два значення (тобто або подія настає з ймовірністю р , або не настає з ймовірністю (1 -р) ) і повторюється n р азів, то випадкова величина Х, що рівна кількості разів настання подій має біноміальний розподіл. Важливим є незалежність послідовності повторів. Мат. сподівання біноміального розподілу = p * n Стандартне відхилення біноміального розподілу = Ймовірність того, що при n спробах буде рівно k успіхів: В Excel: =БИНОМРАСП чи = BINOMDIST , формально де)1(pnp knkn kpp. Ck. XP )1()( ))(. . . 21(). . . 21(. . . 21 )!(! ! knk n C n k
 @ Я. Притул а 3 Біноміальний розподіл: приклад Обладнання, що ви виробляєте, через специфіку технології може бути бракованим з ймовірністю 0. 05. Через місяць ви повинні поставити замовнику 20 одиниць обладнання, причому брак може бути виявленим лише після встановлення. Це важливий для вас клієнт і ви не хочете його підвести, тому вирішуєте відправити замовнику більшу кількість обладнання, щоб при необхідності замінити брак. Скільки штук обладнання оптимально відправити замовнику аби гарантувати 99% якість обладнання?
@ Я. Притул а 3 Біноміальний розподіл: приклад Обладнання, що ви виробляєте, через специфіку технології може бути бракованим з ймовірністю 0. 05. Через місяць ви повинні поставити замовнику 20 одиниць обладнання, причому брак може бути виявленим лише після встановлення. Це важливий для вас клієнт і ви не хочете його підвести, тому вирішуєте відправити замовнику більшу кількість обладнання, щоб при необхідності замінити брак. Скільки штук обладнання оптимально відправити замовнику аби гарантувати 99% якість обладнання?
 @ Я. Притул а 4 Біноміальний розподіл: приклад Ймовірність браку однієї одиниці обладнання = 0. 05, тобто воно справно працює з ймовірністю 0. 95 Якщо ви вирішете відправити лише 20 штук, то ймовірність того, що всі вони справно працюватимуть: =BINOMDIST(20; 0. 95; 0)0. 358486105. 095. 0)20( 02020 20 CXP
@ Я. Притул а 4 Біноміальний розподіл: приклад Ймовірність браку однієї одиниці обладнання = 0. 05, тобто воно справно працює з ймовірністю 0. 95 Якщо ви вирішете відправити лише 20 штук, то ймовірність того, що всі вони справно працюватимуть: =BINOMDIST(20; 0. 95; 0)0. 358486105. 095. 0)20( 02020 20 CXP
 @ Я. Притул а 5 Біноміальний розподіл: приклад Якщо відправити 21 штуку, то ймовірність якісної роботи 20 шт обладнання буде рівна: Р(Х >= 20) =P(X=20)+P(X=21)= = BINOMDIST(20; 21; 0. 95; 0) + BINOMDIST(2 1 ; 21; 0. 95; 0) = = 0. 37641+0. 340562=0. 716972, мало. . Для 22 шт. відповідний показник буде = 0. 905177 Для 23 шт. відповідний показник буде = 0. 974185 Для 24 шт. відповідний показник буде = 0.
@ Я. Притул а 5 Біноміальний розподіл: приклад Якщо відправити 21 штуку, то ймовірність якісної роботи 20 шт обладнання буде рівна: Р(Х >= 20) =P(X=20)+P(X=21)= = BINOMDIST(20; 21; 0. 95; 0) + BINOMDIST(2 1 ; 21; 0. 95; 0) = = 0. 37641+0. 340562=0. 716972, мало. . Для 22 шт. відповідний показник буде = 0. 905177 Для 23 шт. відповідний показник буде = 0. 974185 Для 24 шт. відповідний показник буде = 0.
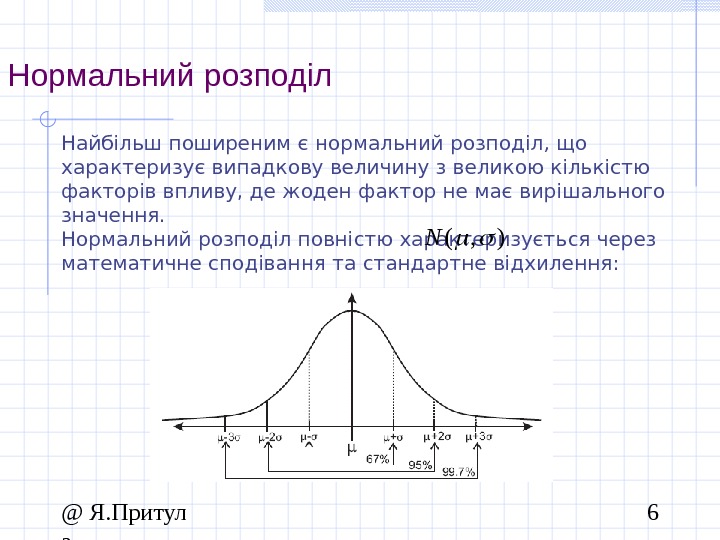
 @ Я. Притул а 6 Нормальний розподіл Найбільш поширеним є нормальний розподіл, що характеризує випадкову величину з великою кількістю факторів впливу, де жоден фактор не має вирішального значення. Нормальний розподіл повністю характеризується через математичне сподівання та стандартне відхилення: ), (N
@ Я. Притул а 6 Нормальний розподіл Найбільш поширеним є нормальний розподіл, що характеризує випадкову величину з великою кількістю факторів впливу, де жоден фактор не має вирішального значення. Нормальний розподіл повністю характеризується через математичне сподівання та стандартне відхилення: ), (N
 @ Я. Притул а 7 Стандартний нормальний розподіл – це нормальний розподіл з математичним сподіванням 0 і стандартним відхиленням 1. Ми будь-який нормальний розподіл Х з параметрами можемо перевести в стандартний нормальний розподіл Z таким перетворенням Часто необхідно працювати з стандартним нормальним розподілом. ), (N X Z
@ Я. Притул а 7 Стандартний нормальний розподіл – це нормальний розподіл з математичним сподіванням 0 і стандартним відхиленням 1. Ми будь-який нормальний розподіл Х з параметрами можемо перевести в стандартний нормальний розподіл Z таким перетворенням Часто необхідно працювати з стандартним нормальним розподілом. ), (N X Z
 @ Я. Притул а 8 Нормальний розподіл Загальна площа під графіком нормального розподілу рівна 1, тому ймовірність попадання випадкової величини в певний інтервал рівна площі під графіком розподілу над цим інтервалом. Для обчислення значень площі використовуватимемо Excel формулу = NORMDIST чи =НОРМРАСП Обернена функція, що за відомої площі (ймовірності) шукає відповідні значення випадкової величини: = NORMINV чи =НОРМОБР Приклад. Обсяг продаж в цьому квартал і склав 21 300 000 грн і перевищив прогноз, що був на рівні 18 000. На наступний квартал обсяг продаж прогнозується на рівні 20 000 з стандартним відхиленням 3 000. Яка ймовірність, що наступний квартал буде дійсно невдалим і продажі будуть менші ніж 15 000.
@ Я. Притул а 8 Нормальний розподіл Загальна площа під графіком нормального розподілу рівна 1, тому ймовірність попадання випадкової величини в певний інтервал рівна площі під графіком розподілу над цим інтервалом. Для обчислення значень площі використовуватимемо Excel формулу = NORMDIST чи =НОРМРАСП Обернена функція, що за відомої площі (ймовірності) шукає відповідні значення випадкової величини: = NORMINV чи =НОРМОБР Приклад. Обсяг продаж в цьому квартал і склав 21 300 000 грн і перевищив прогноз, що був на рівні 18 000. На наступний квартал обсяг продаж прогнозується на рівні 20 000 з стандартним відхиленням 3 000. Яка ймовірність, що наступний квартал буде дійсно невдалим і продажі будуть менші ніж 15 000.
 @ Я. Притул а 9 Нормальний розподіл: приклад З умов, маємо найбільш ймовірне значення обсягів продаж, мат. сподівання = 20 000. Станд. відхилення = 3 000. Треба знайти Р(Х <15 000)= =NORMDIST( 15000000 ; 20000000 ; 3000000 ; 1) = 0. 0478. Якщо б ми хтіли знати ймовірність значення обсягів продаж у розмірі від 16 000 до 23 000, то робимо таке P(16 000<X<23 000)= NORMDIST( 23000000 ; 20000000 ; 3000000 ; 1) — N ORMDIST( 16000000 ; 20000000 ; 3000000 ; 1) = 0. 8413 — 0. 0912=0. 7501. Якщо б ми хтіли знати найгірше значення обсягів продажу з ймовірністю помилки 3% (=0. 03), тоді робимо таке =NORMINV(0. 03; 20000000; 3000000)= 14 357 631.
@ Я. Притул а 9 Нормальний розподіл: приклад З умов, маємо найбільш ймовірне значення обсягів продаж, мат. сподівання = 20 000. Станд. відхилення = 3 000. Треба знайти Р(Х <15 000)= =NORMDIST( 15000000 ; 20000000 ; 3000000 ; 1) = 0. 0478. Якщо б ми хтіли знати ймовірність значення обсягів продаж у розмірі від 16 000 до 23 000, то робимо таке P(16 000<X<23 000)= NORMDIST( 23000000 ; 20000000 ; 3000000 ; 1) — N ORMDIST( 16000000 ; 20000000 ; 3000000 ; 1) = 0. 8413 — 0. 0912=0. 7501. Якщо б ми хтіли знати найгірше значення обсягів продажу з ймовірністю помилки 3% (=0. 03), тоді робимо таке =NORMINV(0. 03; 20000000; 3000000)= 14 357 631.
 @ Я. Притул а 10 Розпод іл Пуасона Розподіл Пуасона подібно до біноміального розподілу дозволяє обрахувати ймовірність настання певної кількості подій, різниця в тому, що для розподілу Пуасона нам не потрібно знати кількості спроб n (тобто можна вважати, що їх є нескінчено багато). Випадкові величини, що мають розподіл Пуасона: • кількість замовлень, отриманих за день; • кількість дефектів в виробленій продукції; • кількість клієнтів, що завтра прийде. Для розподілу Пуасона ймовірність того, що випадкова величина з середнім значення буде рівна а дорівнює В Excel це формула: = POISSON чи =ПУАССОН. ! )( a ea. XP a
@ Я. Притул а 10 Розпод іл Пуасона Розподіл Пуасона подібно до біноміального розподілу дозволяє обрахувати ймовірність настання певної кількості подій, різниця в тому, що для розподілу Пуасона нам не потрібно знати кількості спроб n (тобто можна вважати, що їх є нескінчено багато). Випадкові величини, що мають розподіл Пуасона: • кількість замовлень, отриманих за день; • кількість дефектів в виробленій продукції; • кількість клієнтів, що завтра прийде. Для розподілу Пуасона ймовірність того, що випадкова величина з середнім значення буде рівна а дорівнює В Excel це формула: = POISSON чи =ПУАССОН. ! )( a ea. XP a
 @ Я. Притул а 11 Розпод іл Пуасона: приклад Ви продаєте товар з гарантією. В середньому щотижня ви отримуєте 7 одиниць товару для заміни певної частини по гарантії. Для заміни ви на початку кожного тижня замовляєте запчастини у виробника. Скільки потрібно замовити запчастин на наступний тиждень, щоб з ймовірністю помилки 5% виконати гарантійний ремонт вчасно? Маємо, і нам треба знайти таку найменшу кількість випадків (поломки) а , щоб . Обчислимо цю ймовірність для а=1, 2, . . . Поки не знайдемо те що потрібно: 7 95. 0)(. . )2()1(a. XPXPXP 1 0. 007 8 0. 729 2 0. 030 9 0. 830 3 0. 082 10 0. 901 4 0. 173 11 0. 947 5 0. 301 12 0. 973 6 0. 450 13 0. 987 7 0. 599 14 0. 994 Для а=12 формула є така: =POISSON( 12 ; 7 ; 1 )
@ Я. Притул а 11 Розпод іл Пуасона: приклад Ви продаєте товар з гарантією. В середньому щотижня ви отримуєте 7 одиниць товару для заміни певної частини по гарантії. Для заміни ви на початку кожного тижня замовляєте запчастини у виробника. Скільки потрібно замовити запчастин на наступний тиждень, щоб з ймовірністю помилки 5% виконати гарантійний ремонт вчасно? Маємо, і нам треба знайти таку найменшу кількість випадків (поломки) а , щоб . Обчислимо цю ймовірність для а=1, 2, . . . Поки не знайдемо те що потрібно: 7 95. 0)(. . )2()1(a. XPXPXP 1 0. 007 8 0. 729 2 0. 030 9 0. 830 3 0. 082 10 0. 901 4 0. 173 11 0. 947 5 0. 301 12 0. 973 6 0. 450 13 0. 987 7 0. 599 14 0. 994 Для а=12 формула є така: =POISSON( 12 ; 7 ; 1 )
 @ Я. Притул а 12 Експоненціальний розпод іл Розподіл Пуасона дозволяв обрахувати ймовірність настання певної кількості подій, експоненціальний розподіл дозволяє оцінити час між настаннями цих подій. Приклад таких випадкових величин: • Проміжок часу між приходом нового клієнта. • Час обслуговування одного клієнта. • Період справної роботи устаткування, товару, . . . Ймовірність того, що експоненціально розподілена випадкова величина з середнім значенням буде менша за а дорівнює Для знаходження в Excel використовуємо функцію: =EXP / 1)( a ea. XP x e
@ Я. Притул а 12 Експоненціальний розпод іл Розподіл Пуасона дозволяв обрахувати ймовірність настання певної кількості подій, експоненціальний розподіл дозволяє оцінити час між настаннями цих подій. Приклад таких випадкових величин: • Проміжок часу між приходом нового клієнта. • Час обслуговування одного клієнта. • Період справної роботи устаткування, товару, . . . Ймовірність того, що експоненціально розподілена випадкова величина з середнім значенням буде менша за а дорівнює Для знаходження в Excel використовуємо функцію: =EXP / 1)( a ea. XP x e
 @ Я. Притул а 13 Експоненціальний розпод іл: приклад Час обслуговування одного клієнта дорівнює 1 год. Припустимо, що середня частота приходу клієнтів є 1 клієнт на годину. Скільки треба мати працівників, щоб з ймовірністю 85% гарантувати, що час очікування буде менше 15 хв = 0. 25 год. Один працівник обслуговує одного клієнта.
@ Я. Притул а 13 Експоненціальний розпод іл: приклад Час обслуговування одного клієнта дорівнює 1 год. Припустимо, що середня частота приходу клієнтів є 1 клієнт на годину. Скільки треба мати працівників, щоб з ймовірністю 85% гарантувати, що час очікування буде менше 15 хв = 0. 25 год. Один працівник обслуговує одного клієнта.
 @ Я. Притул а 14 Експоненціальний розпод іл: приклад Маємо . Оскільки наша ймовірність = 0. 85, то ймовірність помилки = 0. 15, що відповідає часу очікування приблизно 10 хв= 0. 16 год. Тобто Тоді після приходу першого клієнта (і, відповідно, зайнятості першого працівника) ми можемо 10 хв + 15 хв не обслуговувати наступних, далі другий працівник починає працювати з наступним клієнтом і ми знов 10 хв + 15 хв не обслуговуємо (починаючи з 11 -ї хвилини), далі стає до роботи третій працівник і знов 10 хв + 15 хв не обслуговуємо (починаючи з 21 -ї хвилини), . . . і т. д. допоки вже звільниться перший працівник. 1 15. 0. )10(1 1/16. 0 хв. XPe
@ Я. Притул а 14 Експоненціальний розпод іл: приклад Маємо . Оскільки наша ймовірність = 0. 85, то ймовірність помилки = 0. 15, що відповідає часу очікування приблизно 10 хв= 0. 16 год. Тобто Тоді після приходу першого клієнта (і, відповідно, зайнятості першого працівника) ми можемо 10 хв + 15 хв не обслуговувати наступних, далі другий працівник починає працювати з наступним клієнтом і ми знов 10 хв + 15 хв не обслуговуємо (починаючи з 11 -ї хвилини), далі стає до роботи третій працівник і знов 10 хв + 15 хв не обслуговуємо (починаючи з 21 -ї хвилини), . . . і т. д. допоки вже звільниться перший працівник. 1 15. 0. )10(1 1/16. 0 хв. XPe
