ху 0 y = а х ,






















pokazatelynaya_funkciya.ppt
- Размер: 2.4 Мб
- Автор: Галина Купрацевич
- Количество слайдов: 26
Описание презентации ху 0 y = а х , по слайдам
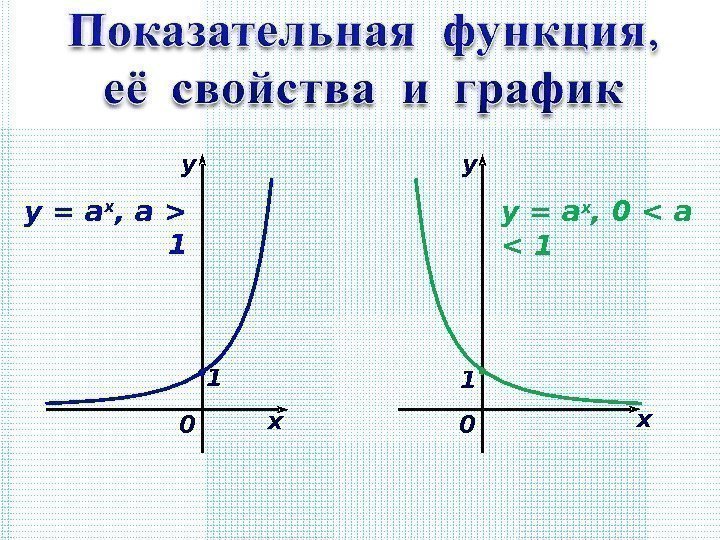
 ху 0 y = а х , а > 1 1 х у 0 y = а х , 0 < а <
ху 0 y = а х , а > 1 1 х у 0 y = а х , 0 < а <
 Содержание • Понятие функции у = аx • Применение показательной ф ункции • Свойства показательной функ ции • График показательной функц ии • Показательные уравнения • Показательные неравенства
Содержание • Понятие функции у = аx • Применение показательной ф ункции • Свойства показательной функ ции • График показательной функц ии • Показательные уравнения • Показательные неравенства
 Понятие показательной функции. Функцию вида y = а х , где а ≠ 1 , a > 0 называют показательной функцией
Понятие показательной функции. Функцию вида y = а х , где а ≠ 1 , a > 0 называют показательной функцией
 1) Например, в теории межпланетных путешествий решается задача об определении массы топлива, необходимого для того, чтобы придать ракете нужную скорость v. Эта масса М зависит от массы m самой ракеты (без топлива) и от скорости v o , с которой продукты горения вытекают из ракетного двигателя. Если не учитывать сопротивление воздуха и притяжение Земли, то масса Показательная функция часто используется при описании различных физических процессов топлива определяется формулой: М = m(e v/v o -1) (формула К. Э. Циолковского). Например, для того чтобы ракета с массой 1 , 5 т имела скорость 8000 м/с, надо взять примерно 80 т топлива.
1) Например, в теории межпланетных путешествий решается задача об определении массы топлива, необходимого для того, чтобы придать ракете нужную скорость v. Эта масса М зависит от массы m самой ракеты (без топлива) и от скорости v o , с которой продукты горения вытекают из ракетного двигателя. Если не учитывать сопротивление воздуха и притяжение Земли, то масса Показательная функция часто используется при описании различных физических процессов топлива определяется формулой: М = m(e v/v o -1) (формула К. Э. Циолковского). Например, для того чтобы ракета с массой 1 , 5 т имела скорость 8000 м/с, надо взять примерно 80 т топлива.
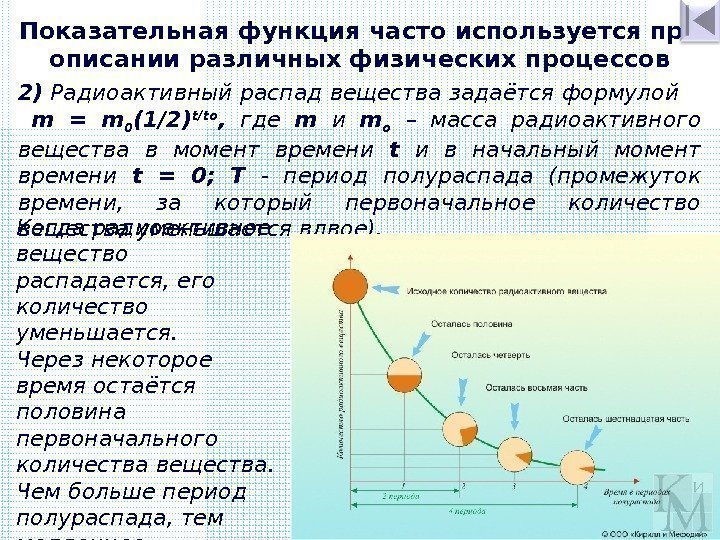
 2) Радиоактивный распад вещества задаётся формулой m = m 0 (1/2) t/tо , где m и m о – масса радиоактивного вещества в момент времени t и в начальный момент времени t = 0; T — период полураспада (промежуток времени, за который первоначальное количество вещества уменьшается вдвое). Показательная функция часто используется при описании различных физических процессов Когда радиоактивное вещество распадается, его количество уменьшается. Через некоторое время остаётся половина первоначального количества вещества. Чем больше период полураспада, тем медленнее распадается вещество.
2) Радиоактивный распад вещества задаётся формулой m = m 0 (1/2) t/tо , где m и m о – масса радиоактивного вещества в момент времени t и в начальный момент времени t = 0; T — период полураспада (промежуток времени, за который первоначальное количество вещества уменьшается вдвое). Показательная функция часто используется при описании различных физических процессов Когда радиоактивное вещество распадается, его количество уменьшается. Через некоторое время остаётся половина первоначального количества вещества. Чем больше период полураспада, тем медленнее распадается вещество.
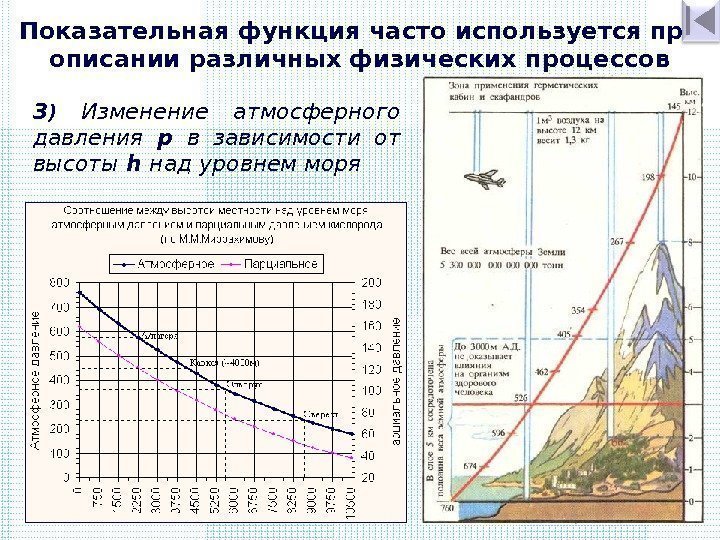
 3 ) Изменение атмосферного давления p в зависимости от высоты h над уровнем моря описывается формулой p = p о ∙ a k , где p о – атмосферное давление над уровнем моря, а – некоторая постоянная. Показательная функция часто используется при описании различных физических процессов Барограф метеорологический анероидный Погодная станция Oregon Scientific
3 ) Изменение атмосферного давления p в зависимости от высоты h над уровнем моря описывается формулой p = p о ∙ a k , где p о – атмосферное давление над уровнем моря, а – некоторая постоянная. Показательная функция часто используется при описании различных физических процессов Барограф метеорологический анероидный Погодная станция Oregon Scientific
 3 ) Изменение атмосферного давления p в зависимости от высоты h над уровнем моря. Показательная функция часто используется при описании различных физических процессов
3 ) Изменение атмосферного давления p в зависимости от высоты h над уровнем моря. Показательная функция часто используется при описании различных физических процессов
 8. a n ∙ a m = a n + m a n : a m = a n − m (a n ) m = a nm (ab) n = a n ∙ b n (a : b) n = a n : b n 3. а) При а > 1 функция возрастает на R ; б) при 0 < а 0 4. Ни четная функция, ни нечетная. 1. D(y) = (-∞; +∞), E(y) = ( 0; +∞). . 5. Не ограничена сверху, ограничена снизу. 6. Не имеет ни наибольшего, ни наименьшего значений. 7. Непрерывна. Выпукла вниз.
8. a n ∙ a m = a n + m a n : a m = a n − m (a n ) m = a nm (ab) n = a n ∙ b n (a : b) n = a n : b n 3. а) При а > 1 функция возрастает на R ; б) при 0 < а 0 4. Ни четная функция, ни нечетная. 1. D(y) = (-∞; +∞), E(y) = ( 0; +∞). . 5. Не ограничена сверху, ограничена снизу. 6. Не имеет ни наибольшего, ни наименьшего значений. 7. Непрерывна. Выпукла вниз.
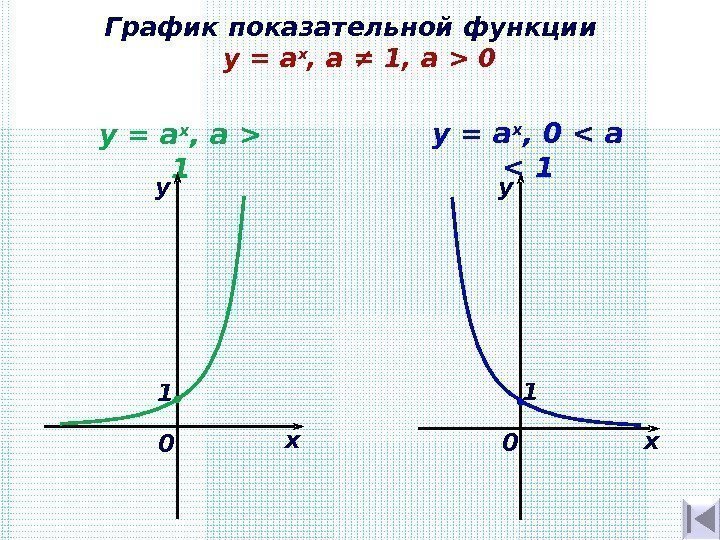
 График показательной функции y = а х , а ≠ 1, a > 0 ху 0 y = а х , а > 1 1. y = а х , 0 < а < 1 ху
График показательной функции y = а х , а ≠ 1, a > 0 ху 0 y = а х , а > 1 1. y = а х , 0 < а < 1 ху
 2. Если 0 < а 1 справедливо ⟺ x < 0 ; б) неравенство a x 0. Свойства сравнения выражений вида а х , а ≠ 1, a > 0 1. Если 0 < а 1 , то равенство a r = a s справедливо тогда и только тогда, когда r = s. . 3. Если а > 1 , то a) неравенство a x > 1 справедливо ⟺ x > 0 ; б) неравенство a x < 1 справедливо ⟺ x 1 , то a) неравенство a f(x) > a h(x) справедливо ⟺ f(x) > h(x) ; б) неравенство a f(x) < a h(x) справедливо ⟺ f(x) < h(x). 5. Если 0 < а a h(x) справедливо ⟺ f(x) < h(x) ; б) неравенство a f(x) h(x).
2. Если 0 < а 1 справедливо ⟺ x < 0 ; б) неравенство a x 0. Свойства сравнения выражений вида а х , а ≠ 1, a > 0 1. Если 0 < а 1 , то равенство a r = a s справедливо тогда и только тогда, когда r = s. . 3. Если а > 1 , то a) неравенство a x > 1 справедливо ⟺ x > 0 ; б) неравенство a x < 1 справедливо ⟺ x 1 , то a) неравенство a f(x) > a h(x) справедливо ⟺ f(x) > h(x) ; б) неравенство a f(x) < a h(x) справедливо ⟺ f(x) < h(x). 5. Если 0 < а a h(x) справедливо ⟺ f(x) < h(x) ; б) неравенство a f(x) h(x).
 Показательные уравнения Уравнения вида a f(x) = а h( х ) , где а ≠ 1 , a > 0 называют показательными уравнениями a f(x) = а h( х ) f(x) = h( х )⟺ Методы решения показательных уравнений: 1. Функционально-графический метод. 2. Метод уравнивания показателей. 3. Метод введения новой переменной.
Показательные уравнения Уравнения вида a f(x) = а h( х ) , где а ≠ 1 , a > 0 называют показательными уравнениями a f(x) = а h( х ) f(x) = h( х )⟺ Методы решения показательных уравнений: 1. Функционально-графический метод. 2. Метод уравнивания показателей. 3. Метод введения новой переменной.
 Показательные уравнения. Примеры 5: 5 642 22 642 42 Ответ x x xx Пример 1 2: 2 5, 05, 32 3 1 3 1 5, 05, 32 Ответ x x Пример 2 Пример 3 4; 2: 4 , 2 086 833 55 2122 8332 Ответ xx xx xxx
Показательные уравнения. Примеры 5: 5 642 22 642 42 Ответ x x xx Пример 1 2: 2 5, 05, 32 3 1 3 1 5, 05, 32 Ответ x x Пример 2 Пример 3 4; 2: 4 , 2 086 833 55 2122 8332 Ответ xx xx xxx
 Показательные уравнения. Примеры 5: 5 25 55 55 555 25 1 55: 51 04, 05 52, 0 25 421 2 25, 0 25, 0 Ответ x xx xx Пример 4 Пример 5 2: 2 42 064 , 6 0242 0, 2 024222 02424 1 212 22 1 Ответ х переменнойисходнойк. Вернемся tусловиюетуднеt tt tt тогдаtгдеt. Пусть х х хх хх хx
Показательные уравнения. Примеры 5: 5 25 55 55 555 25 1 55: 51 04, 05 52, 0 25 421 2 25, 0 25, 0 Ответ x xx xx Пример 4 Пример 5 2: 2 42 064 , 6 0242 0, 2 024222 02424 1 212 22 1 Ответ х переменнойисходнойк. Вернемся tусловиюетуднеt tt tt тогдаtгдеt. Пусть х х хх хх хx
 Показательные уравнения. Примеры Пример 622 2 1 2 2 22 42 0 234 , 23 06 25 0, 2 62 25 2 22 хx хxхx переменнойисходнойк. Вернемся tусловиюетуднеt tt tt tt. Пусть 5, 1 64 442 22 2 2 х х хх хx ): []; (х х : ОДЗ 22 2 2 02 2 2. 5, 1: Ответ
Показательные уравнения. Примеры Пример 622 2 1 2 2 22 42 0 234 , 23 06 25 0, 2 62 25 2 22 хx хxхx переменнойисходнойк. Вернемся tусловиюетуднеt tt tt tt. Пусть 5, 1 64 442 22 2 2 х х хх хx ): []; (х х : ОДЗ 22 2 2 02 2 2. 5, 1: Ответ
 Показательные уравнения. Примеры Пример 7 ; 6 , 2 0128 0, 2 012282 01222 012264 212 336 33 tt tt tt. Пусть ххх хх хх х х. 6 log 3 ; 3: 2 Ответ 6 log 3 3 6 log 3 13 6222 2 233 хх хх или переменнойисходнойк. Вернемся хх
Показательные уравнения. Примеры Пример 7 ; 6 , 2 0128 0, 2 012282 01222 012264 212 336 33 tt tt tt. Пусть ххх хх хх х х. 6 log 3 ; 3: 2 Ответ 6 log 3 3 6 log 3 13 6222 2 233 хх хх или переменнойисходнойк. Вернемся хх
 Показательные уравнения. Примеры Пример 8 корнейнетttt ttt tt тогдаtгдеt. Пусть х хх хх 033 0333 092 , 0, 3 099227 992 927 9 999 81 2 27 27 9 99 81 2 279 2 22 223 23 2 2 3 2 1 33 х переменнойисходнойк. Вернемся х. 1: Ответ
Показательные уравнения. Примеры Пример 8 корнейнетttt ttt tt тогдаtгдеt. Пусть х хх хх 033 0333 092 , 0, 3 099227 992 927 9 999 81 2 27 27 9 99 81 2 279 2 22 223 23 2 2 3 2 1 33 х переменнойисходнойк. Вернемся х. 1: Ответ
 Показательные уравнения. Примеры Пример 9 (однородное уравнение)тогдаtгдеt. Пусть тогдана. Разделим х хх х х x х ххx ххx , 0, 3 5 06 3 5 13 3 5 5 0 9 96 9 1513 9 55 , 9 096151355 0 9 9 54151355 095415135 2 2 112 2 log 1 2 35 5 3 35 2 , 5 3 06135 3521 2 хх или переменнойисходнойк. Вернемся tt tt хх. 2 log; 1: 3 5 Ответ
Показательные уравнения. Примеры Пример 9 (однородное уравнение)тогдаtгдеt. Пусть тогдана. Разделим х хх х х x х ххx ххx , 0, 3 5 06 3 5 13 3 5 5 0 9 96 9 1513 9 55 , 9 096151355 0 9 9 54151355 095415135 2 2 112 2 log 1 2 35 5 3 35 2 , 5 3 06135 3521 2 хх или переменнойисходнойк. Вернемся tt tt хх. 2 log; 1: 3 5 Ответ
 Показательные уравнения. Примеры Пример 10 (составление отношения) 2 11 3 4 33 43 33 34 033. . , 33: 4334 133144 3344 3434 1 1 1111 11 x x кт x х x ххxx xx xxхx xххx. 2: Ответ
Показательные уравнения. Примеры Пример 10 (составление отношения) 2 11 3 4 33 43 33 34 033. . , 33: 4334 133144 3344 3434 1 1 1111 11 x x кт x х x ххxx xx xxхx xххx. 2: Ответ
 Показательные уравнения. Примеры Пример 11 (скрытая замена переменной) 32 2 324 12416, 014 , 4 1 : 1 32, 0, 32 1343232, 43232 2 1 2 t t Dtt t видприметуравнение t тогдаtгдеt. Пусть что. Заметим х хх xx + =
Показательные уравнения. Примеры Пример 11 (скрытая замена переменной) 32 2 324 12416, 014 , 4 1 : 1 32, 0, 32 1343232, 43232 2 1 2 t t Dtt t видприметуравнение t тогдаtгдеt. Пусть что. Заметим х хх xx + =
 Показательные уравнения. Примеры Пример 11 (скрытая замена переменной) 2 1 2 3232 32 1 32 3232 : 1 2 x x или переменнойисходнойк. Вернемсяx хх + = 4 2 1 2 3232 2 x xx х. 2; 2: Ответ
Показательные уравнения. Примеры Пример 11 (скрытая замена переменной) 2 1 2 3232 32 1 32 3232 : 1 2 x x или переменнойисходнойк. Вернемсяx хх + = 4 2 1 2 3232 2 x xx х. 2; 2: Ответ
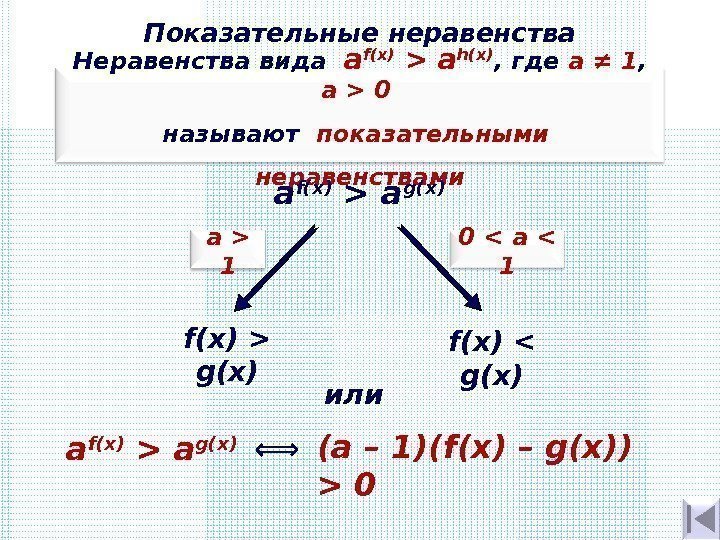
 Показательные неравенства Неравенства вида a f(x) > а h( х ) , где а ≠ 1 , a > 0 называют показательными неравенствами a f(x) > а g( х ) f(x) > g( х ) f(x) < g( х )0 < а 1 a f(x) > а g( х ) ⟺ (а – 1)( f(x) – g(x)) > 0 или
Показательные неравенства Неравенства вида a f(x) > а h( х ) , где а ≠ 1 , a > 0 называют показательными неравенствами a f(x) > а g( х ) f(x) > g( х ) f(x) < g( х )0 < а 1 a f(x) > а g( х ) ⟺ (а – 1)( f(x) – g(x)) > 0 или
 Показательные неравенства. Примеры ; : Ответ x x то, Rнавозрастает монотонноуфункция. к. т txx 55 642 222 642 42 Пример 1 ; : Ответ x , , x то, Rнаубываетмонотонно уфункция. к. т t, , x 22 50532 3131 31 50532 532 Пример
Показательные неравенства. Примеры ; : Ответ x x то, Rнавозрастает монотонноуфункция. к. т txx 55 642 222 642 42 Пример 1 ; : Ответ x , , x то, Rнаубываетмонотонно уфункция. к. т t, , x 22 50532 3131 31 50532 532 Пример
 Показательные неравенства. Примеры Пример 3 ; 42; : ; 42; 4 , 2 086: . . 086 833 , 5, 0. . 5, 0 21 222 8332 Ответ х xx xxфн xx xxx то. Rнаубываетмонотонно уфункциякт txxx + + − х
Показательные неравенства. Примеры Пример 3 ; 42; : ; 42; 4 , 2 086: . . 086 833 , 5, 0. . 5, 0 21 222 8332 Ответ х xx xxфн xx xxx то. Rнаубываетмонотонно уфункциякт txxx + + − х
 Показательные неравенства. Примеры Пример 4 1 01, 02. . 2111112 02 0, 3 2 2 3 2 3 32 3 2 03. . , 3: 32322 272188 2 2333 3 3 2 3 3 33323 t tтоtлюбыхдляttкт ttttt tt tгдеt. Пусть кт x xx х xх х x ххxxхx
Показательные неравенства. Примеры Пример 4 1 01, 02. . 2111112 02 0, 3 2 2 3 2 3 32 3 2 03. . , 3: 32322 272188 2 2333 3 3 2 3 3 33323 t tтоtлюбыхдляttкт ttttt tt tгдеt. Пусть кт x xx х xх х x ххxxхx
 Показательные неравенства. Примеры Пример 40 3 2 , 1 3 2. . , 3 2 1 3 2 : 0 x Rнаубываетуцияфтоакт переменнойисходнойк. Вернемся xxx . 0; : Ответ
Показательные неравенства. Примеры Пример 40 3 2 , 1 3 2. . , 3 2 1 3 2 : 0 x Rнаубываетуцияфтоакт переменнойисходнойк. Вернемся xxx . 0; : Ответ
 Используемые материалы 1. Алгебра и начала анализа. 11 класс. В 2 ч. Ч. 1. Учебник для общеобразоват. учреждений (профильный уровень) / А. Г. Мордкович, П. В. Семенов. 2 -е изд. , стер. – М. : Мнемозина, 2008 2. http: //www. physics. org/ — 3. http: //www. mathematics. ru/courses/algebra/design/index. htm — 4. http: //www. megabook. ru/index. asp — Большая энциклопедия Кирилла и Мефодия
Используемые материалы 1. Алгебра и начала анализа. 11 класс. В 2 ч. Ч. 1. Учебник для общеобразоват. учреждений (профильный уровень) / А. Г. Мордкович, П. В. Семенов. 2 -е изд. , стер. – М. : Мнемозина, 2008 2. http: //www. physics. org/ — 3. http: //www. mathematics. ru/courses/algebra/design/index. htm — 4. http: //www. megabook. ru/index. asp — Большая энциклопедия Кирилла и Мефодия

