ВЫПУКЛЫЙ АНАЛИЗ ЛЕКЦИЯ 5 2. ВЫПУКЛЫЕ МНОЖЕСТВА












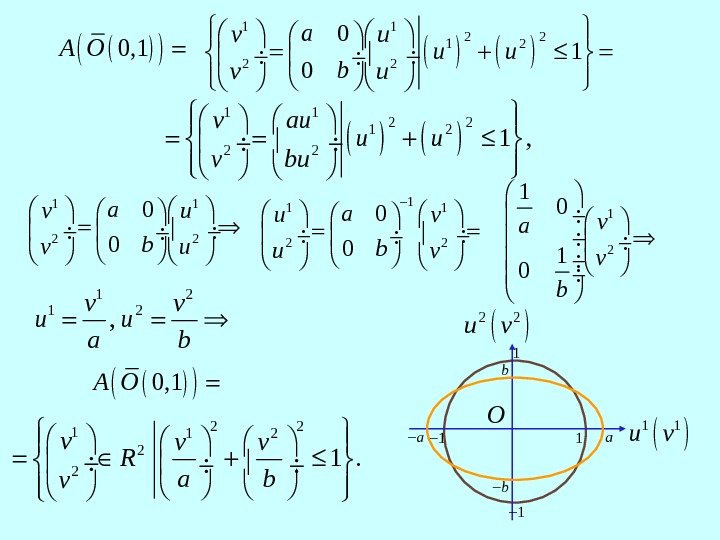




lekciya_5.ppt
- Размер: 1.7 Мб
- Автор: Progressive Sound
- Количество слайдов: 18
Описание презентации ВЫПУКЛЫЙ АНАЛИЗ ЛЕКЦИЯ 5 2. ВЫПУКЛЫЕ МНОЖЕСТВА по слайдам
 ВЫПУКЛЫЙ АНАЛИЗ ЛЕКЦИЯ 5 2. ВЫПУКЛЫЕ МНОЖЕСТВА
ВЫПУКЛЫЙ АНАЛИЗ ЛЕКЦИЯ 5 2. ВЫПУКЛЫЕ МНОЖЕСТВА
 2. ВЫПУКЛЫЕ МНОЖЕСТВА (ПРОДОЛЖЕНИЕ) 2. 2. Аффинные множества. 2. 4. Операции над выпуклыми множествами. 2. 3. Размерность множества.
2. ВЫПУКЛЫЕ МНОЖЕСТВА (ПРОДОЛЖЕНИЕ) 2. 2. Аффинные множества. 2. 4. Операции над выпуклыми множествами. 2. 3. Размерность множества.
 2. 2. Аффинные множества. Определение 2. Множество n RM называется аффинным, если для всех 1 1 2 , , u u M R справедливо включение 1 2(1 ). u u M Геометрический смысл данного определения состоит в том, что аффинное множество вместе с любыми своими точками проходящую через эти точки. содержит и всю прямую, Очевидно, что аффинные множества выпуклы. Пустые и одноточечные множества принимаются аффинными по определению. Теорема 2. Любой сдвиг аффинного множества является аффинным множеством. Доказательство. Пусть n. A R аффинное множество Полагаем 0. M A u Требуется доказать, что множество M является аффинным. 0. n u Rи Действительно, для всех Muu 21, и 1 R имеем 1 1 0 2 2 0, , A A u a u 1 2, a a A 1 21 u u u 1 0 2 01 a u 1 2 01 A афинноеa a u 6 44 7 4 48 0. A u M Теорема доказана.
2. 2. Аффинные множества. Определение 2. Множество n RM называется аффинным, если для всех 1 1 2 , , u u M R справедливо включение 1 2(1 ). u u M Геометрический смысл данного определения состоит в том, что аффинное множество вместе с любыми своими точками проходящую через эти точки. содержит и всю прямую, Очевидно, что аффинные множества выпуклы. Пустые и одноточечные множества принимаются аффинными по определению. Теорема 2. Любой сдвиг аффинного множества является аффинным множеством. Доказательство. Пусть n. A R аффинное множество Полагаем 0. M A u Требуется доказать, что множество M является аффинным. 0. n u Rи Действительно, для всех Muu 21, и 1 R имеем 1 1 0 2 2 0, , A A u a u 1 2, a a A 1 21 u u u 1 0 2 01 a u 1 2 01 A афинноеa a u 6 44 7 4 48 0. A u M Теорема доказана.
 Определение 3. Множество n RL. u v L если для всех 1 , R следует и Lvu, называется подпространством, n R пространства когда для всех 1 R и Lvu, следует Lvu и. u LДоказать, что множество n RL будет подпространством тогда и только тогда, Теорема 3. Пусть n. A R — аффинное множество, и 0. A Тогда A подпространство. Доказательство. Для всех 1 , , u v A R имеем 1 0 , 1 определение афинного множества u u A 1 1 2 2 2 u v 1 1 1 2 1. 2 2 A в силу A u v A 6 4 44 7 4 4 48 6 4 4 7 4 4 8 Теорема доказана. Упражнение. Достаточность. L L L u v L 6 4 7 4 8 n R Все пространство и любое его подпространство являются аффинными множествами. Доказательство. Необходимость. n L R Пусть Тогда. u v L Для 1, 1 u v L и для 0. u L подпространство.
Определение 3. Множество n RL. u v L если для всех 1 , R следует и Lvu, называется подпространством, n R пространства когда для всех 1 R и Lvu, следует Lvu и. u LДоказать, что множество n RL будет подпространством тогда и только тогда, Теорема 3. Пусть n. A R — аффинное множество, и 0. A Тогда A подпространство. Доказательство. Для всех 1 , , u v A R имеем 1 0 , 1 определение афинного множества u u A 1 1 2 2 2 u v 1 1 1 2 1. 2 2 A в силу A u v A 6 4 44 7 4 4 48 6 4 4 7 4 4 8 Теорема доказана. Упражнение. Достаточность. L L L u v L 6 4 7 4 8 n R Все пространство и любое его подпространство являются аффинными множествами. Доказательство. Необходимость. n L R Пусть Тогда. u v L Для 1, 1 u v L и для 0. u L подпространство.
 Теорема 4. Всякое аффинное множество n A R представимо в виде 0, 2 A L u где L подпространство, а 0 u произвольная точка множества . A , Aоднозначно определяемое множеством Доказательство. Пусть 0. u A Положим 0. L A u В силу теоремы 2 множество L аффинное, Тогда по теореме 3 L подпространство. В самом деле, пусть 1 1 1, . 3 L A u u A Из (2) следует 0. A u L Тогда имеет место включение 1 0. Au u L По свойству подпространств Пусть. u L 1 0 L L u u u L 1 0 u L u u 2 0 1 A L u u 64 7 48 причем 00. u A L 13 1 1. L u A u L 64 7 48 Таким образом, доказано, что 1. L L Тогда 1 LL и теорема доказана. Аналогично доказывается обратное вложение 1. L LДокажем, что 1. u LУбедимся, что оно не зависит от выбора 0. u точки 1 A u
Теорема 4. Всякое аффинное множество n A R представимо в виде 0, 2 A L u где L подпространство, а 0 u произвольная точка множества . A , Aоднозначно определяемое множеством Доказательство. Пусть 0. u A Положим 0. L A u В силу теоремы 2 множество L аффинное, Тогда по теореме 3 L подпространство. В самом деле, пусть 1 1 1, . 3 L A u u A Из (2) следует 0. A u L Тогда имеет место включение 1 0. Au u L По свойству подпространств Пусть. u L 1 0 L L u u u L 1 0 u L u u 2 0 1 A L u u 64 7 48 причем 00. u A L 13 1 1. L u A u L 64 7 48 Таким образом, доказано, что 1. L L Тогда 1 LL и теорема доказана. Аналогично доказывается обратное вложение 1. L LДокажем, что 1. u LУбедимся, что оно не зависит от выбора 0. u точки 1 A u
 Определение 4. Подпространство L из представления (1) параллельным множеству . Aподпространством, называется 01 A L u Дадим геометрическую иллюстрацию полученных результатов. При 2 n подпространство представляет собой прямую, проходящую через начало координат, Теорема 3 утверждает, что для любой прямой на плоскости существует единственная прямая, 1 u 2 u 0 2 1 u ku b 2 1 u kuа аффинное множество – произвольную прямую на плоскости. проходящая через начало координат, ей параллельная. Теорема 5. Доказательство аналогично доказательству теоремы 1. Пересечение любого числа аффинных множеств является аффинным множеством.
Определение 4. Подпространство L из представления (1) параллельным множеству . Aподпространством, называется 01 A L u Дадим геометрическую иллюстрацию полученных результатов. При 2 n подпространство представляет собой прямую, проходящую через начало координат, Теорема 3 утверждает, что для любой прямой на плоскости существует единственная прямая, 1 u 2 u 0 2 1 u ku b 2 1 u kuа аффинное множество – произвольную прямую на плоскости. проходящая через начало координат, ей параллельная. Теорема 5. Доказательство аналогично доказательству теоремы 1. Пересечение любого числа аффинных множеств является аффинным множеством.
 2. 3. Размерность множества. Определение 5. Пусть . n U R Пересечение всех аффинных множеств, содержащих множество , U называется аффинной оболочкой множества U Из определения множества aff. U следует, что оно аффинное, Определение 6. Подпространство параллельное , aff. Uи вложено в любое другое аффинное множество, содержащее . U содержит множество U и обозначается через . Lin. U содержащее . UТаким образом, аффинная оболочка множества U представляет собой аффинное множество, минимальное O U 1 u 2 u 3 u aff. U Lin. Uназывается несущим подпространством U множества обозначается через . aff. U и
2. 3. Размерность множества. Определение 5. Пусть . n U R Пересечение всех аффинных множеств, содержащих множество , U называется аффинной оболочкой множества U Из определения множества aff. U следует, что оно аффинное, Определение 6. Подпространство параллельное , aff. Uи вложено в любое другое аффинное множество, содержащее . U содержит множество U и обозначается через . Lin. U содержащее . UТаким образом, аффинная оболочка множества U представляет собой аффинное множество, минимальное O U 1 u 2 u 3 u aff. U Lin. Uназывается несущим подпространством U множества обозначается через . aff. U и
 Определение 7. Размерностью множества n RU называется размерность несущего пространства его аффинной оболочки. Согласно принятому определению отрезок , 1 0, 1 u v u u v соединяющий две точки , , , n u v R u v имеет размерность 1, так как его аффинной оболочкой является прямая 1 , 1. aff u v u u R Размерность шара n RRu. O, 0 равна. n 1 u 2 u 3 u O u v 1 u 2 u 3 u O , aff u v, Lin u v
Определение 7. Размерностью множества n RU называется размерность несущего пространства его аффинной оболочки. Согласно принятому определению отрезок , 1 0, 1 u v u u v соединяющий две точки , , , n u v R u v имеет размерность 1, так как его аффинной оболочкой является прямая 1 , 1. aff u v u u R Размерность шара n RRu. O, 0 равна. n 1 u 2 u 3 u O u v 1 u 2 u 3 u O , aff u v, Lin u v
 2. 4. Операции над выпуклыми множествами. К числу операций над выпуклыми множествами, сохраняющих их выпуклость относятся: взятия линейной алгебраической комбинации и линейного преобразования. Теорема 6. Любая линейная комбинация конечного числа выпуклых множеств выпукла. Доказательство. Пусть 1, , n m. U U R L выпуклые множества Для всех , u v U справедливо представление , , 1, , . u v i i ia a U i m L 1 , i. U m u i i iu a 1 , i. U m v i i iv a Тогда при всех 1, 0 имеем 1 1. i i im u v Uвыпуклост i U i i ь a a 6 4 4 4 7 4 4 48 (1 )u v 1 1 (1 ) m m u v i i i a a операции пересечения, 1. m i i i U U и 1 1 (1 )i i m m u v i i a a
2. 4. Операции над выпуклыми множествами. К числу операций над выпуклыми множествами, сохраняющих их выпуклость относятся: взятия линейной алгебраической комбинации и линейного преобразования. Теорема 6. Любая линейная комбинация конечного числа выпуклых множеств выпукла. Доказательство. Пусть 1, , n m. U U R L выпуклые множества Для всех , u v U справедливо представление , , 1, , . u v i i ia a U i m L 1 , i. U m u i i iu a 1 , i. U m v i i iv a Тогда при всех 1, 0 имеем 1 1. i i im u v Uвыпуклост i U i i ь a a 6 4 4 4 7 4 4 48 (1 )u v 1 1 (1 ) m m u v i i i a a операции пересечения, 1. m i i i U U и 1 1 (1 )i i m m u v i i a a
 Из выпуклости множества i. U следует 1 , u v i i ia a U Тогда 1 (1 ) 1. i m u v i U i i i u v a a 6 4 4 4 7 4 4 48 Теорема доказана. Теорема 7. Пусть n RU выпуклое множество и 0, 0. Тогда . 1 U U U Доказательство. Вложение UUU было доказано в предыдущей лекции в общем случае без предположения о выпуклости множества U и положительности чисел и. В условиях теоремы докажем обратное вложение 1 m i i i U 1 (1 ) 1. i i im u v Uвыпу i i i клость U U i u v a a 6 4 4 4 7 4 4 48 1, , , i m L. U. U U U
Из выпуклости множества i. U следует 1 , u v i i ia a U Тогда 1 (1 ) 1. i m u v i U i i i u v a a 6 4 4 4 7 4 4 48 Теорема доказана. Теорема 7. Пусть n RU выпуклое множество и 0, 0. Тогда . 1 U U U Доказательство. Вложение UUU было доказано в предыдущей лекции в общем случае без предположения о выпуклости множества U и положительности чисел и. В условиях теоремы докажем обратное вложение 1 m i i i U 1 (1 ) 1. i i im u v Uвыпу i i i клость U U i u v a a 6 4 4 4 7 4 4 48 1, , , i m L. U. U U U
 Будем предполагать, что 0. В противном случае 0 и формула (1) Пусть . u U U Тогда 1 2. выпуклость Uu u U 1 2, , U U u u u U }}0 20 1 , u u u Таким образом, u U и теорема доказана. Пусть n RU и A квадратная матрица n го порядка. Определение 8. Образом множества U при линейном преобразовании A называется множество. A U v Au u U очевидна. 0 0 0. 1 U U U 64 7 48 0, 0, 1 U U U
Будем предполагать, что 0. В противном случае 0 и формула (1) Пусть . u U U Тогда 1 2. выпуклость Uu u U 1 2, , U U u u u U }}0 20 1 , u u u Таким образом, u U и теорема доказана. Пусть n RU и A квадратная матрица n го порядка. Определение 8. Образом множества U при линейном преобразовании A называется множество. A U v Au u U очевидна. 0 0 0. 1 U U U 64 7 48 0, 0, 1 U U U
 Теорема 8. При линейном преобразовании Доказательство. Ограничимся доказательством выпуклости образа линейного преобразования. Пусть 1 2 , v v A U Для всех 1, 0 выполнено 1 21. Uвыпуклость A u u 6 4 4 7 4 48 1 2 1 v v 1 2 1 Au Au В силу выпуклости множества U имеет место включение 1 21. u u U Тогда 1 21 v v и выпуклость множества UA доказана. Пример 5. Пусть 0 2, , 0 a n A b 0, 1 U O множества образ непустого компактного выпуклого является непустым компактным выпуклым множеством. , , i i iv Au u U 1, 2. i 1 21 U A u u 6 4 4 7 4 48 A U 1 2 2 1. u u
Теорема 8. При линейном преобразовании Доказательство. Ограничимся доказательством выпуклости образа линейного преобразования. Пусть 1 2 , v v A U Для всех 1, 0 выполнено 1 21. Uвыпуклость A u u 6 4 4 7 4 48 1 2 1 v v 1 2 1 Au Au В силу выпуклости множества U имеет место включение 1 21. u u U Тогда 1 21 v v и выпуклость множества UA доказана. Пример 5. Пусть 0 2, , 0 a n A b 0, 1 U O множества образ непустого компактного выпуклого является непустым компактным выпуклым множеством. , , i i iv Au u U 1, 2. i 1 21 U A u u 6 4 4 7 4 48 A U 1 2 2 1. u u
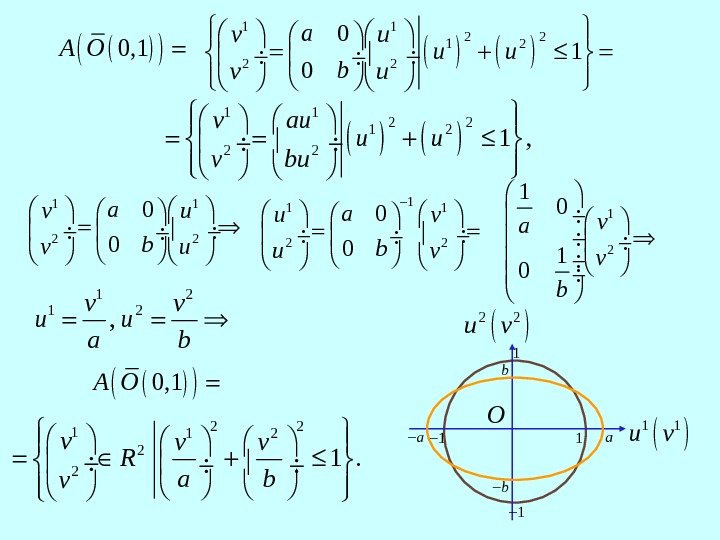 1 1 2 2 21 , v au u u v bu 0, 1 A O 1 1 2 2 2 0 1 0 a v u u u b v u 2 211 2 2 21. vv v R a bv 1 2 , v v u u a b 1 1 2 2 0 0 av u bv u 0, 1 A O 11 1 2 2 0 0 au v bu v 1 2 1 0 va v b 1 1 u v 2 2 u v O 1 1 aa b b
1 1 2 2 21 , v au u u v bu 0, 1 A O 1 1 2 2 2 0 1 0 a v u u u b v u 2 211 2 2 21. vv v R a bv 1 2 , v v u u a b 1 1 2 2 0 0 av u bv u 0, 1 A O 11 1 2 2 0 0 au v bu v 1 2 1 0 va v b 1 1 u v 2 2 u v O 1 1 aa b b
 Упражнение 1. Пусть 1 2 1 1 2 2 1 27 2 14, 5 6 30, 3 8 24, u u u U u u u Построить множество , A U где 2 0. 0 3 A Решение. 1 2 1 27 2 14, 1 5 6 30, 2 3 8 24, 3 u u u 1 u 2 u 0 2 4 6 8 246810246 2 4 6 (1) (3)1 20 7, u u 1 1 20 5, u u 23. UПостроение множества Убедиться в его выпуклости 1 22 0. u u 1 26 0. u u (2)1 20 3, u u 1 28 0. u u
Упражнение 1. Пусть 1 2 1 1 2 2 1 27 2 14, 5 6 30, 3 8 24, u u u U u u u Построить множество , A U где 2 0. 0 3 A Решение. 1 2 1 27 2 14, 1 5 6 30, 2 3 8 24, 3 u u u 1 u 2 u 0 2 4 6 8 246810246 2 4 6 (1) (3)1 20 7, u u 1 1 20 5, u u 23. UПостроение множества Убедиться в его выпуклости 1 22 0. u u 1 26 0. u u (2)1 20 3, u u 1 28 0. u u
 A U 1 21 1 1 22 2 1 2 7 2 14, 5 6 30, . 3 8 24, u u v u A u u v u u u Построение множества . A U 1 1 1 1 2 2 2 3 30 2 0 0 0 3 v u v v v A v u v v v A U 1 1 1 2 2 3 2 1 1 1 2 2 37 2 14, 5 6 30, 3 8 24, v v v v 1 2 1 27 2 14, 1 2 3 5 2 30, 2 2 3 8 24 3 2 3 v v v
A U 1 21 1 1 22 2 1 2 7 2 14, 5 6 30, . 3 8 24, u u v u A u u v u u u Построение множества . A U 1 1 1 1 2 2 2 3 30 2 0 0 0 3 v u v v v A v u v v v A U 1 1 1 2 2 3 2 1 1 1 2 2 37 2 14, 5 6 30, 3 8 24, v v v v 1 2 1 27 2 14, 1 2 3 5 2 30, 2 2 3 8 24 3 2 3 v v v
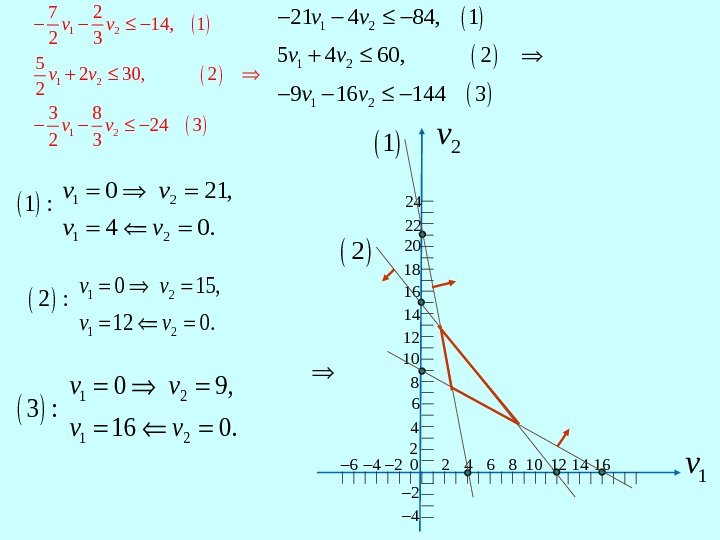
 1 2 1 221 4 84, 1 5 4 60, 2 9 16 144 3 v v v 1 2 1 27 2 14, 1 2 3 5 2 30, 2 2 3 8 24 3 2 3 v v v 1 2 0 21, 4 0. v v 1 : 1 2 0 15, 12 0. v v 2 : 1 2 0 9, 16 0. v v 3 : 0 2 4 6 8 246810246 2 4 121416 10 12 14 16 18 20 22 24 1 v 2 v
1 2 1 221 4 84, 1 5 4 60, 2 9 16 144 3 v v v 1 2 1 27 2 14, 1 2 3 5 2 30, 2 2 3 8 24 3 2 3 v v v 1 2 0 21, 4 0. v v 1 : 1 2 0 15, 12 0. v v 2 : 1 2 0 9, 16 0. v v 3 : 0 2 4 6 8 246810246 2 4 121416 10 12 14 16 18 20 22 24 1 v 2 v
 0 2 4 6 8 246810246 2 4 121416 10 12 14 16 18 20 22 24 1 1 v u 2 2( )v u (3) U A U
0 2 4 6 8 246810246 2 4 121416 10 12 14 16 18 20 22 24 1 1 v u 2 2( )v u (3) U A U

