ВЫПУКЛЫЙ АНАЛИЗ ЛЕКЦИЯ 3 n R 1. ПРОСРАНСТВО

ВЫПУКЛЫЙ АНАЛИЗ ЛЕКЦИЯ 3 n R 1. ПРОСРАНСТВО ПОДМНОЖЕСТВ (ПРОДОЛЖЕНИЕ)

1. ПРОСРАНСТВО ПОДМНОЖЕСТВ. n R 1. 3. Алгебраические линейные комбинации подмножеств . n R 1. 4. Расстояние Хаусдорфа. (ПРОДОЛЖЕНИЕ) (продолжение)

Тогда их любая алгебраическая комбинация 1 m i i i. A A является компактным множеством. Действительно, имеют место включения 0, , 1, , . i i. A O A i m L следует их ограниченность и конечность величин max , 1, , . u Ai u i. A i m L Тогда для всех Aa справедливо неравенство Из компактности множеств n m. RAA, , 1 10, m i i i. A O A что и означает ограниченность множества 1. m i i i A A Теорема 3. Пусть множества 1, , n m. A A RL компактны. Доказательство. 1 i. Am i i ia a m 1 ax i u A m i i i a 1 m i i i. A Докажем ограниченность множества. A Пусть последовательность , , 1, 2, j jx x A j L сходится к . x 1. 3. Алгебраические линейные комбинации подмножеств (продолжение) Действительно, справедливо представление Надо доказать, что. x A Докажем замкнутость. A множества 1 , 1, , m i i i а a a A i m L

, 1, , , 1, 2, , . i ija Aijm L L }1 , i i m A j jx a Из компактности множеств i. A для всех1, , im. L можно считать, что 1, , . im. L 0, i ijia a A 1 2 m A A A L 1 11 1 21 1 1 1, , A AA ja a a A L L 1 1 1 2 1 11 11 1 10, , jk k k A AA a a A L L Действительно, 2 1 1 22 2 2 , , , j A A k k k A a a a A L L 2 2 1 2 2 22 22 2 20, , jk k k A AA a a A L L 1 11 11 2 2 11 1 mm i i i m a a x L 1 2 22 2 1 1 2 2 2, , i m m i a ax L 1 1 1 22 , j j i i m m i m j j a a a j ax L L L L L Lx

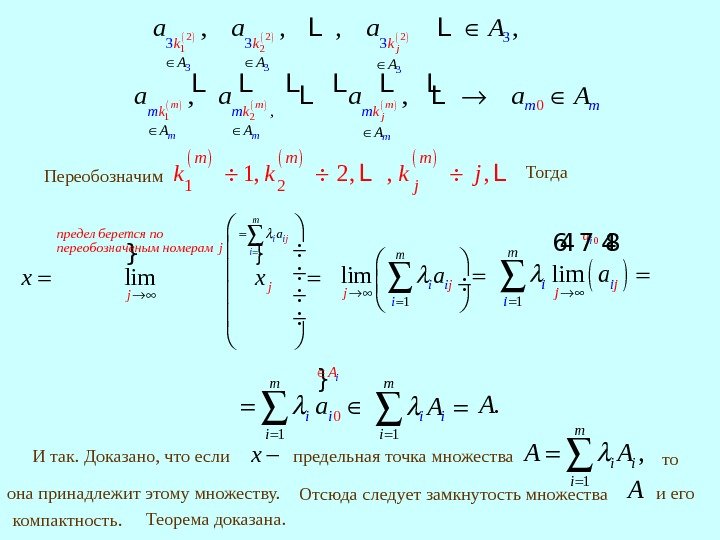
L L L 1 2 0, , , m m j m mk k k A m mm m AA m a a A L L 3 33 2 2 2 1 233 3 3 , , j A AA k k k a a a A L LТогда } 0 1 i. A m i i i a }}1 lim i jiпредел берется по переобозначеным номерам j jj a x x 0 1 limi a jj m i i i a 64 7 48 Теорема доказана. Переобозначим 1 2 1, 2, , , m m m jk k k j L L И так. Доказано, что если x предельная точка множества 1 , m i i i A A она принадлежит этому множеству. то Отсюда следует замкнутость множества A и его компактность. 1 m i i i A . A 1 limi i i m jj a

Теорема 3. Пусть множества 1 2, n A A R компактны. Упражнение 1. Тогда их любая алгебраическая комбинация 1 1 2 2 A A A является компактным множеством. 2. m Доказать теорему 3 при Доказательство. Ограниченность. Для всех Aa справедливо неравенство 1 1 2 20, , A O A A 1 2 1 1 2 2 A A a a a 2 1 2 max 1 1 2 2 i u A u A a a 1 1 2 2 A A что и доказывает ограниченность множества. A Доказательство замкнутости. Надо доказать, что . x AПусть последовательность , jx сходится к . n x R , 1, 2, jx A j L Действительно, справедливо представление 1 12 2 1 a a x 21 2 221 2, a a x L L 1 1 2 2 j j a a jx L Lx

в силу компактности множества 1 A 1 1 1 2 1 1, , ja a a A L L Из последовательности можно выделить подпоследовательность1 1 21 11 1 10, , . jk k k a a A L L 2 2 2 10 222 2 2 , , . k k k a a A L L в силу компактности множества 2 AИз последовательности 1 1 222 2 2 , , jk k k a a a AL L можно выделить подпоследовательность Тогда. Переобозначим 2 2 2 1, 2, , , j k k k j L L 1 1 2 2. A A A 1 1 2 2 lim j j ja a 1 1 2 2 lim j j j ja a 1 2 1 1 2 20 0 A A a a }1 1 2 2 lim j j предел берется по переобозначеным номерам j jj j a a jx x x

Теорема доказана. И так. Доказано, что еслиx предельная точка множества 1 1 2 2, A A A она принадлежит этому множеству. то Отсюда следует замкнутость множества A и его компактность. Непосредственно проверяется, что для любых чисел , и любых множеств n RVU, выполняются следующие свойства. 1) ; U U 2) 1 ; U U 3) . U V Эти свойства являются следствием соответствующих свойств векторов из пространства . n. R Однако пространство подмножеств n R нельзя считать линейным пространством, хотя бы потому, что не всегда выполняется равенство . 2 U U U Пусть 0, 1 , 1, 1. U O Тогда с одной стороны Пример 3. 1 0, 1 U O 0, 1 , O

2 1 0, 1 Теорема U O 0, 1 1 0, 1 O O 0, 2 , O а с другой 1 0, 1 Теорема U U O O 0 0, 2. O Вместо равенства (2). U U U Действительно, пусть . u U Тогда существует Uu 0 такой, что 0. u u Отсюда следует 1 11 1 0, 1 U O в общем случае 2 U U U справедливо лишь одностороннее вложение. U U 0 u u 0 0 u u

1. 4. Расстояние Хаусдорфа. Пусть Определение 17. Величина называется расстоянием Хаусдорфа между множествами U и. V U V 1 2 min 0 , U V V U , U V т. е. что для любых множеств n RWVU, , справедливо Покажем, что введенное понятие действительно является расстоянием, 1) , 0; U V 2) 3) , , ; U V V U ; U V, 0 U V 4) WVVUWU, , , Подробного доказательства требует лишь пункт 4). Приведем его. , . V W , , U V Пусть 1 2 max , . , n U V R- компактные множества. Обозначим 1 min 0 , U V 2 min 0. V U Тогда , U V

0, W O 0, , V W O 0, , 3 U W O 0, U O 0, , V U O 0, . 4 W U O что и доказывает требуемое свойство. 0, 0, W O U V O 0, 0, U W O O 0, 0, U O W V O 0, 0, W U O O Из (3) и (4) выводим , U W , , , U V V W Тогда , U V , V W , U V

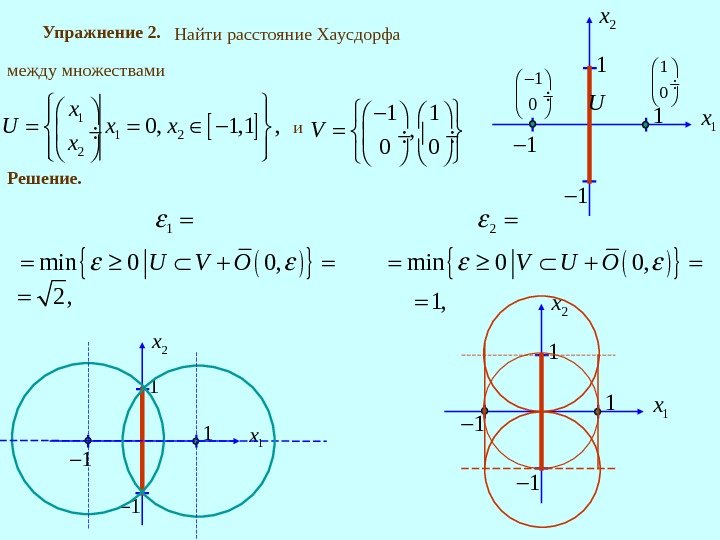
Упражнение 2. 1 1 2 2 0, 1, 1 , x U x x x и 1 1 , 0 0 V Решение. 12 Найти расстояние Хаусдорфа между множествами 1 1 1 11 x 2 x U 1 0 2 , min 0 0, U V O min 0 0, V U O 1, 1 11 x 2 x

1 2, max , U V R R max 2 , 1 2. Таким образом, Упражнение 3. Найти расстояние Хаусдорфа между шарами 1 1 2 2, , , n n O u u R u u Решение. 1 2 1 min 0 , , 0, min 0 , , O u O O u 1 u 2 u 1 2 1 u u 2 1 1 u u 1 2 1 u u Аналогично

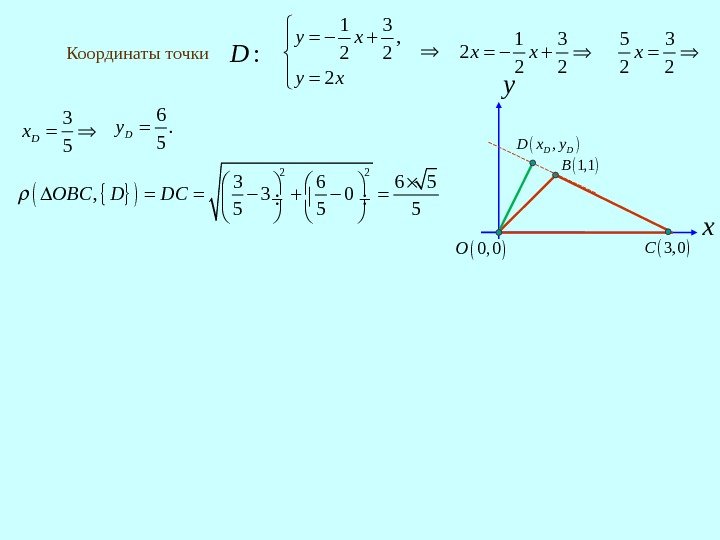
2 1 2 min 0 , , 0, min 0 , , O u O O u 2 1 u u 1 2, , , max , O u R R 2 1 max , u u Упражнение 4. Дан треугольник OBC координатами своих вершин 0, 0 , 1, 1 , 3, 0. O B C Найти расстояние Хаусдорфа между этим треугольником и точкой , D 0, 0 O 1, 1 B 3, 0 C x y , D DD x yявляющейся пересечением высоты, O на сторону. BC с этой стороной. опущенной из вершины Решение. Уравнение стороны : BC 1 0 1 1 1 3 y x 1 1 1 2 y x 1 3 2 2 y x 1 2 BCk 2. BDk Уравнение высоты : BD 0 2 y x 2 1 max , . u u

0, 0 O 1, 1 B 3, 0 C x y , D DD x y. Координаты точки : D 1 3 , 2 2 2 y x 1 3 2 2 2 x x 3 5 Dx 5 3 2 2 x 6. 5 Dy 2 2 3 6 6 5 , 3 0 5 5 5 O