ВЫПУКЛЫЙ АНАЛИЗ ЛЕКЦИЯ 2 n R 1. ПРОСРАНСТВО

ВЫПУКЛЫЙ АНАЛИЗ ЛЕКЦИЯ 2 n R 1. ПРОСРАНСТВО ПОДМНОЖЕСТВ (ПРОДОЛЖЕНИЕ)

1. ПРОСРАНСТВО ПОДМНОЖЕСТВ. n R 1. 3. Алгебраические линейные комбинации подмножеств . n R(ПРОДОЛЖЕНИЕ)

1. 3. Алгебраические линейные комбинации подмножеств . n R Пусть n m. RAA, , 1 и 1 1, , . m. R L Множество 1 , 1, , m i i ia a a A i m L будем называть алгебраической линейной комбинацией множеств m. AA, , 1 с коэффициентами 1 1, , . m. R L В частности, если , , n n A R B b R то множество называется сдвигом множества A на вектор . b. Определение 15. 1 m i i i. A A u a b a A A B A b

Имеет место равенство 1 2, . 1 O u u R R Теорема 1. 1 1 2 2 , , O u R 1 2 1 1 2 2, u u R 1 2 u u } 1 2 u u u 1 2 u u 1 2 1 2 R R u u 64 7 48 1 2 R R 1 2, . u O u u R R Доказано, что 1 2, . O u u R R 1 1 2 2, , O u R Пусть 1 1 2 2, , . u O u R Тогда 1 1 2 2 , , 1 2 , O u Ru u u Доказательство. O 1 u 1 R 2 u 2 R 1 2 u u 1 2 R R

Пусть 1 2 , . u O u u R R Тогда 1 2. R R Если 0, 1 1 2 2 , , . O u R Пусть теперь 0. Тогда возможно представление 0 , 1, 2. i i. R i Обозначим Докажем обратное вложение. 1 20 u u u 6 44 7 4 48 то 1 20 u u u 1 21 2, R R 22 2 1 2. u u u Тогда 1 1 2 , u u u 1 2 u u 1 1 1 2 u u uu 2 2 1 2 u u uu 1 2 1 2 1 u u u 6 7 8 u 1 2 u uuu u 1 1 2 2, 1 2 , O u R u u u

Заметим, что , 1, 2. i i i. R i 1 2 i i iu u u i i u u 1 2 iu u u 6 4 7 4 8 1 2 u u u Таким образом, 1 2 1 1 2 2, , O u u R R O u R и равенство (1) 1 1 2 2, , O u R i i i u u R 1 1 2 2 1 2, , , . 1 O u R O u u R R доказано. Имеет место равенство 0, 0, . k O R O k R Теорема 2. , , 1, 2 i i iu O u R i 1 1 2 2 , 1 2 , O u R u u u

При 0 k справедливость доказываемого равенства очевидна. Пусть 0 k и 0, . u k O R Тогда 0, u O k R 00, u O R Доказательство. 0 , u ku } 0 0 ku u ku } 0 R k u k R Обратно, если 0, , u O k R u k R то полагаем 0, u k O R k R R k Теорема доказана. 1 v u k } 1 1 u k v u k 0, v O R } 0, O R u k v Из теорем 1, 2 следует, 0 0 0 , , 0 0, u O u R O u O R 64 7 48 Ru. O, 0 можно представить в виде что любой шар 00, . u O R 0, 0, . k O R O k R 0, 0, . O k R k O R } 1 k R u k

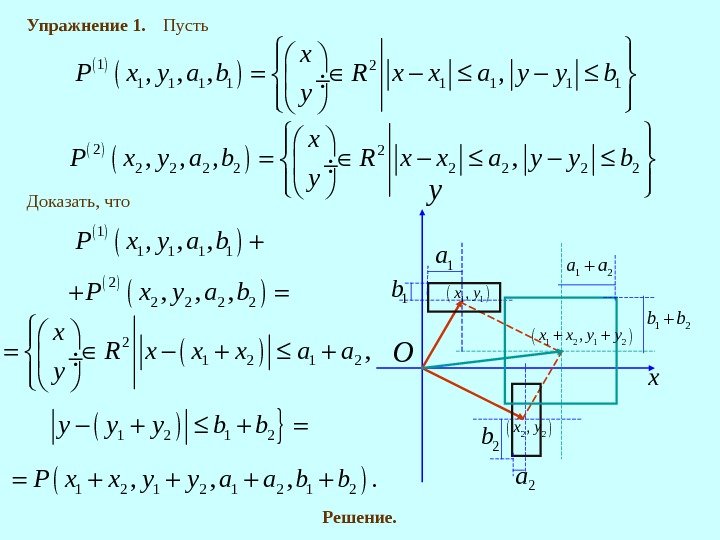
Упражнение 1. Пусть 12 1 1 1 1, , x P x y a b R x x a y y b y 22 2 2 2 2, , x P x y a b R x x a y y b y Доказать, что 2 1 2, x R x x x a a y 1 2 y y y b b 1 1 1, , , P x y a b 2 2 2, , , P x y a b y O 1 1, x y x 2 2, x y 2 b 2 a 1 a 1 b 1 2, x x y y 1 2 a a 1 2 b b Решение. 1 2 1 2, , , . P x x y y a a b b

Пусть 1 2 1 1 2 2, , , . u P x y a b Тогда 2 22 2 2 2 22 , , x x P x y a b R x x a y y b yy 1 2 u u xx x u yy y 1 12 1 1 1 11 , , , x x P x y a b R x x a y y b yy Имеет место неравенство 1 2 1 2 1 2 ux x x 1 2 1 2 x x a a 1 2 , u u x x x y y y Докажем вложение 1 2 1 1 2 2 1 2 1 2, , , , , . P x y a b P x x y y a a b b

Аналогично устанавливается, что 1 2. uy y y b b 1 2. ux x x a a Тогда u ux y 2 1 2 1 2, x R x x x a a y y y b b y и вложение 1 2 1 1 2 2 1 2 1 2, , , , , . P x y a b P x x y y a a b b доказано. Установим обратное вложение. 1 2 1 1 2 2, , , . P x y a b 1 2 1 2, , , P x x y y a a b b Пусть u u x y 2 1 2 1 2, . x R x x x a a y y y b b y

Тогда 1 20. x ux x x Пусть0. x Сделаем представление 0 , 1, 2. xi ia i 1 2, x x x Обозначим 22 2 1 2. x u x x x 11 1 1 2, x u x x x Очевидно, что 1 1 1 2 x x ux x xx 1 2, u uxx x x xx 1 2 x x 2 2 1 2 x x ux x xx С другой стороны 1 2, 1, 2, u x iix ix i u x ix i x x x a ix x Таким образом, 1 2 1 1 2 2, , 2. ux x x a

Если 1 20 , x u x x x то 1 2 ux x x снова имеет место. Аналогично, устанавливаем, что } } 1 2 1 1 2 2 1 2 3. y y b u y y by y y Из (2) и (3) следует } } 1 2 1 1 2 2 1 2 1 , , 2, , P x y a b x a u u P y b xx x yy y 1 2 1 1 2 2, , , . P x y a b 1 2 1 2 1 2 1 1 2 2, , , , , . P x x y y a a b b P x y a b Вложение доказано, а значит и равенство 1 2 1 1 2 2 1 2 1 2, , , , , . P x y a b P x x y y a a b b и равенство (2) } } 1 2 1 2 1 1 2 2, , 2 x x ux x x a

Множество. Определение 16. называется открытой окрестностью. U множества U U Множество , n U v R v u u U U U называется замкнутой окрестностью множества. U : , . n U v R u U v u Упражнение 2. Доказать равенство 0, , U U O : , . n U v R u U v u где Решение. Пусть : . v U u U v u 0, w v u w O 0, 0, OU v w u O U Полагаем w v u 0, . U U O

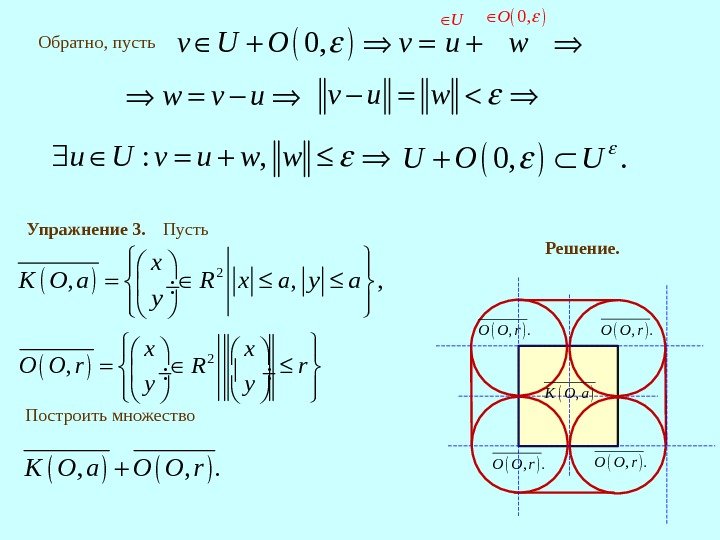
Обратно, пусть 0, 0, OUv U O v u w w v u 0, . U O U : , u U v u w w Упражнение 3. Пусть 2 , , , x K O a R x a y 2 , x x O O r R r y y Построить множество , , . K O a O O r Решение. , K O a , . O O r, . O O r