ВЫПУКЛЫЙ АНАЛИЗ ЛЕКЦИЯ 17 6. ТЕОРЕМЫ ОБ ОТДЕЛИМОСТИ

ВЫПУКЛЫЙ АНАЛИЗ ЛЕКЦИЯ 17 6. ТЕОРЕМЫ ОБ ОТДЕЛИМОСТИ ВЫПУКЛЫХ МНОЖЕСТВ

6. ТЕОРЕМЫ ОБ ОТДЕЛИМОСТИ ВЫПУКЛЫХ МНОЖЕСТВ 6. 1. Проекция точки на множество 6. 2. Отделимость точки и множества. 6. 3. Отделимость выпуклых множеств.

6. 1. Проекция точки на множество Определение 1. Пусть . n. U Rn. Rv Проекцией точки на множество U называется точка ( ) , Uw P v U удовлетворяющая условию v w u U inf. u U w v u v Справедливо следующее утверждение. Теорема 1. Пусть n. RU замкнутое множество. Тогда для всякой точки n Rv существует ее проекция на это множество. Если множество U выпукло, то проекция единственна и равенство )(v. Pw. U имеет место тогда и только тогда, когда , 0, . 1 w v u w u U Доказательство. Задача построения )(v. Pw. U — проекции точки v на множество U сводится к минимизации функции 1 : , I U R определенной

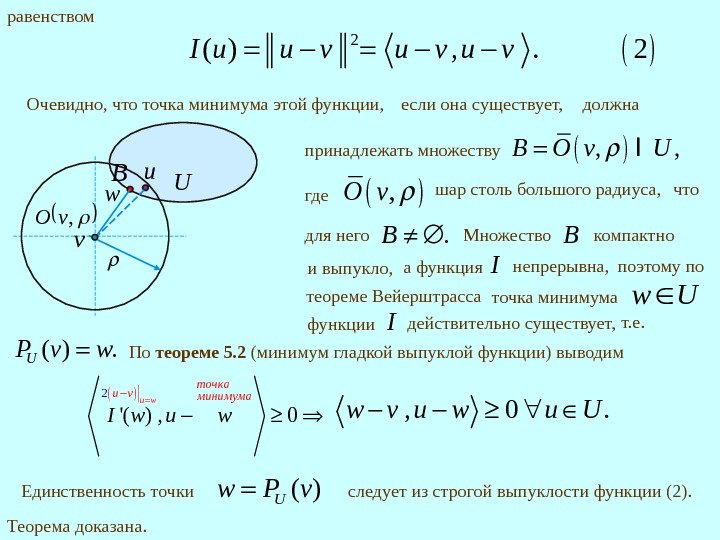
равенством 2 ( )I u u v Очевидно, что точка минимума этой функции, где , O v шар столь большого радиуса, а функция I непрерывна, действительно существует, т. е. ( ). UP v w По теореме 5. 2 ( минимум гладкой выпуклой функции) выводим 2 ‘( ) , 0 u w точкаu vминимума I w u w Единственность точки ( )Uw P v следует из строгой выпуклости функции ( 2 ). Теорема доказана. если она существует, принадлежать множеству , , B O v UI должна для него. B что точка минимума Uw функции I , 0. w v u w u U Множество B компактно и выпукло, , . 2 u v v w u UB , v. O поэтому по теореме Вейерштрасса

6. 2. Отделимость точки и множества. Точку и выпуклое множество можно разделить гиперплоскостью так, Теорема 2. Пусть n RU выпуклое множество. Тогда для любой точки Uvint существует вектор 0, l такой, что , , l u l v u U то 2 , , , . l u l v l u U Доказательство. Сначала рассмотрим случай . v U Множество U замкнуто и выпукло. Тогда согласно теореме 1 существует проекция Uv. Pw. U)( точки v на множество , U причем , 0, . (1)w v u w u U Заметим, что 0, w v так как. v Uесли при этом , v U Положим . l w v Тогдаполупространствах, что они будут находиться в разных замкнутых определяемых этой гиперплоскостью. v U l u w

, , w v l u v w v u v 1 0 , w v u w 6 44 7 4 48 и для рассматриваемого случая теорема доказана. Пусть теперь \ int. v U U Тогда Uv и существует последовательность , 2, 1, , k. Uvvvkk существует вектор 0 kl такой, что , , , . 1 k k kl u l v u U Можно считать, что 1, 1, 2. kl k L Если бы это было не так, Переходя, если это необходимо, к подпоследовательности, При этом 1 0. l В неравенстве (1) устремим k в бесконечность. В пределе получим требуемое соотношение. Для каждого номера , 2, 1 k по доказанному выше неравенства (1) следовало бы поделить на величину 0, 1, 2, kl k L то обе части. kl l принимаем, что Теорема доказана. u U 2 , l u v l 2 , , l u l v l , ww v u v , l l w v 2 , l l l 2 , , , l u l v l u U , , , l u l v u U v U kv , w v u w w v

Доказанной теореме придадим следующий геометрический смысл. v U l u , l Пусть v U вектор существование которого доказано 0 l в теореме 2. и v. U и множестворазделяющей точку гиперплоскости Этот вектор будет нормальным для , , , 2 n l u R l u При изменении величины гиперплоскость будет перемещаться параллельно самой себе. Она будет оставаться разделяющей, если , , , inf , . u Ul u l v u u U U l u l v l u 6 4 4 7 4 4 8 , , . n l u R l u Полупространство, содержащее множество , U имеет вид Для него гиперплоскость , l служит границей. Пусть теперь \ int. v U U U В этом случаеv U и должно выполняться неравенство inf , , . u U l u l v Тогда inf , , u U l u l v , , inf , u U l v l u , l v , , , . v l l l v

Гиперплоскость, , l l v называется опорной U. v U в точке к множеству Полупространство , , l l v называется опорным. U в точке. v U к множеству Вектор l называют опорным вектором к множеству U в точке. v v Ul, , l l v. В этом случае разделяющая гиперплоскость , , l l v и множество U имеют общую точку. v Эта точка определяется из условия , min , . v Ul v l l v может служить опорным к множеству U в некоторой точке. v l U Заметим, что если множество U компактно, 0, 1 l S то любой вектор l. U , , l l v v l , min , v U V l v l U l v l l v Множество совокупность всех точек v l может содержать более одного элемента. U, , l l v. V l l

U, , l l v. V l l , , l l v Таким образом , , min , . 2 n v U l u R l u l v называется опорным множеством к множеству U в направлении. l вектора V l Множество Опорные гиперплоскости , , l l v v V l для всех совпадают между собой. и опорные полупространства , , l l v Эту гиперплоскость и полупространство к множеству U в направлении l векторабудем называть опорной гиперплоскостью и опорным полупространством и обозначать символами, , l l соответственно. , min , . (3) n v U l u R l u l v

Упражнение. Для множества 2 2 2 1 20 5 xx y U R y построить опорное множество, 2 2. l отвечающее направлению Решение. Запишем уравнение касательной к эллипсу, перпендикулярную направлению. l Имеем 1 y k x b y x b l x y V l Vx Координата Vx является корнем уравнения 22 1 20 5 x bx 22 4 20 x x b 2 2 2 4 8 4 20 0 x x xb b 2 2 5 8 4 20 0 x xb b 2 2 2 1, 2 4 16 20 100 4 4 100. 5 5 b b b x

Корень должен быть только один. Тогда 5, 4, 1 V Vb x y Из чертежа видно, что 4. 1 V l 2 2 , min 4 , . . 1 , , . v U V V x не подходит т к y l v l 2 2 2 1, 2 4 16 20 100 4 4 100. 5 5 b b b x l x y V l Vx

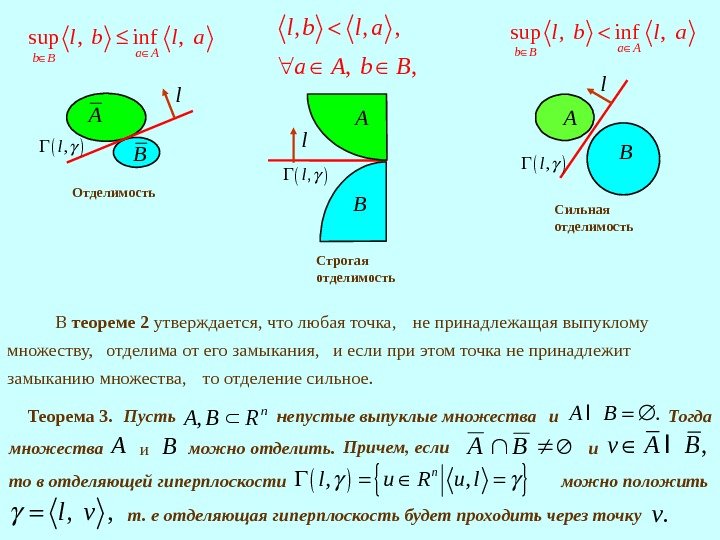
6. 3. Отделимость выпуклых множеств. Результаты предыдущего пункта допускают обобщение на случай, когда вместо точки берется выпуклое множество. Определение 2. Будем говорить, что множества n RBA, отделимы, если для некоторого вектора 0, 1 l S справедливо неравенство sup , inf , a Ab B l b l a строго отделимы, если , , , l b l a a A b B сильно отделимы, если знак неравенства в (2) Геометрический смысл отделимости множеств состоит в существовании гиперплоскости 1, , , 0, 1 , , nl u R u l l S R Такую гиперплоскость называют отделяющей (строго, сильно). sup , inf , 2 a Ab B l b l a строгий. 1 : , , , 2 R l b l a a A b B для которой AB находятся в разных по отношению к ней полупространствах. множества и Ниже дается геометрическая интерпретация различных случаев отделения.

В теореме 2 утверждается, что любая точка, не принадлежащая выпуклому множеству, отделима от его замыкания, и если при этом точка не принадлежит замыканию множества, то отделение сильное. A B Отделимость l , l sup , inf , a Ab B l b l a A B l , l Сильная отделимость sup , inf , a Ab B l b l a Теорема 3. Пусть n. RBA, непустые выпуклые множества и . A B I Тогда множества A и. B можно отделить. Причем, если BA и , v A BI то в отделяющей гиперплоскости , , nl u R u l можно положить , , l v , , , l b l a a A b B A B l. Строгая отделимость , l B т. е отделяющая гиперплоскость будет проходить через точку. v

Доказательство. Рассмотрим множество , . U A B u a b a A b B Множество U выпукло. Поскольку , A B I постольку 0. U Тогда по теореме 2 существует вектор 0, 1 , l S что Отсюда выводим , , 0 0, . a b l u U , 0 l a b Пусть теперь , . a A b B Найдутся последовательности , , k ka a b b В силу неравенства (3) будет выполняться , , 1, 2, . k ka A b B k L , , . 3 l a l b a A b B , , , 1, 2, k kl a l b k L Переходя в последнем неравенстве к пределу при , k получим , , , 4 l a l b a A b B что и означает выполнение неравенства (2). sup , inf , 2 a Ab B l b l a

Пусть, наконец, . v A B I Тогда с одной стороны из Av вытекает, что , , l b l v b B а с другой из Bv и снова (4) следует , , , . l a l v a A Таким образом, , . l v Теорема доказана. и (4) , , , 4 l a l b a A b B Теорема 4. Пусть n RBA, непустые выпуклые замкнутые множества, одно из которых ограничено и . A B I Тогда множества A и. B сильно отделимы. Доказательство. В условиях доказываемой теоремы множество BAU замкнуто. Действительно, пусть для определенности множество A ограничено, u предельная точка множества , U и последовательность , ku u , , 1, 2, k ka A b B k L где , U A B k k ku a b В силу ограниченности ( компактности) множества A , , , l b l v l a a A b B sup , inf , a Ab B l b l a

из последовательности ka можно извлечь сходящуюся подпоследовательность . jka a A . jkb b a u , A B u a b что и означает его замкнутость. , u A B U Из условия BA следует, что 0. U U такой, что 2 , , . a b l u U По т еореме 2 существует 0, l вектор 2 , , , . l a b l a A b B Отсюда выводим 2 , , 0 , l u l l u U В результате предельного jk получим перехода при . b B В силу замкнутости, B выполнено включение множества b a u Тогда , U Таким образом, u предельная точка множества U принадлежит множеству. j j j a A k k k u U b a u Изk k k u a b следует k k kb a u j jk A U ka u b A U

2 , , , l a b l a A b B 2 inf , sup , a A b Bl a l b l Заметим, что любая гиперплоскость, , , nl u R l u где sup , , inf , a Ab B l b l a Теорема доказана. inf , sup , a A b Bl a l b 2 , , , l a l b l a A b B Может служить сильно отделяющей для множеств A. B и sup , b B l b inf , a Al a