ВЫПУКЛЫЙ АНАЛИЗ ЛЕКЦИЯ 14 4. СВЯЗЬ МЕЖДУ ВЫПУКЛЫМИ

ВЫПУКЛЫЙ АНАЛИЗ ЛЕКЦИЯ 14 4. СВЯЗЬ МЕЖДУ ВЫПУКЛЫМИ ФУНКЦИЯМИ И ВЫПУКЛЫМИ МНОЖЕСТВАМИ

4. СВЯЗЬ МЕЖДУ ВЫПУКЛЫМИ ФУНКЦИЯМИ И ВЫПУКЛЫМИ МНОЖЕСТВАМИ 4. 1. Надграфик выпуклой функции. 4. 2. Множество Лебега выпуклой функции. 4. 3. Опорная функция подмножества пространства . n R 4. 4. Опорные функции выпуклых оболочек подмножеств пространства. n R

4. 1. Надграфик выпуклой функции. Между выпуклыми функциями и выпуклыми множествами существует определенная связь. Определение 1. Надграфиком (эпиграфом) функции , I определенной на множестве , n U R называется множество 1 , ( ). nu epi I R u U I u На рисунке закрашенное множество является надграфиком функции 1 : , . I a b R Теорема 1. Для того чтобы функция , I определенная на выпуклом множестве , n. U R была выпуклой, необходимо и достаточно, Доказательство. Пусть функция I выпуклая. Для любых двух точек Iepizz u z 21 2 2 2 1 1 1, , , составим их выпуклую комбинацию 1 2 1 , 0, 1. 1 u u u 1 21 z z z выпуклым множеством. чтобы ее надграфик был Необходимость. u a b I 1 z 2 z

Из выпуклости множества U следует, что 1 21 , u u u U а из выпуклости функции I вытекает неравенство 1 2 1 I u u которое влечет за собой включение . u z epi I Необходимость доказана. Достаточность. Пусть множество Iepi выпукло в 1 n R и 1 2, , 0, 1. u u U Тогда 1 2 1 2 , u u z epi I I u 1 2 1 , 1 u u epi I I u Отсюда в силу определения множества Iepi следует 1 2( ) 1 ( )I u что и означает выпуклость функции . I Теорема доказана. 1 21 z z 1 21 2( ) 1 ( )I u 1, ( )nu R u U I u 1 21 I u u u a b I 1 z 2 z 1 u 2 u z u

Упражнение. Построить множество точек на плоскости, координаты которых, x y удовлетворяют системе неравенств 2 2 4 3 0, 2 0, y x x x y y и доказать, что это множество выпуклое. Решение. 2 1 24 3 0 1, 3, x x x y 2 1 22 0 1, 2 y y 2 2 4 3 0, 2 0, y x x x y y 2 2 4 3, 2 y x x x y y 2 4 0, 2 1 0 dy x dx dx y dy 2, 1 2 x y 4 8 3 1, ; 1 1 9 2 4 y x x y

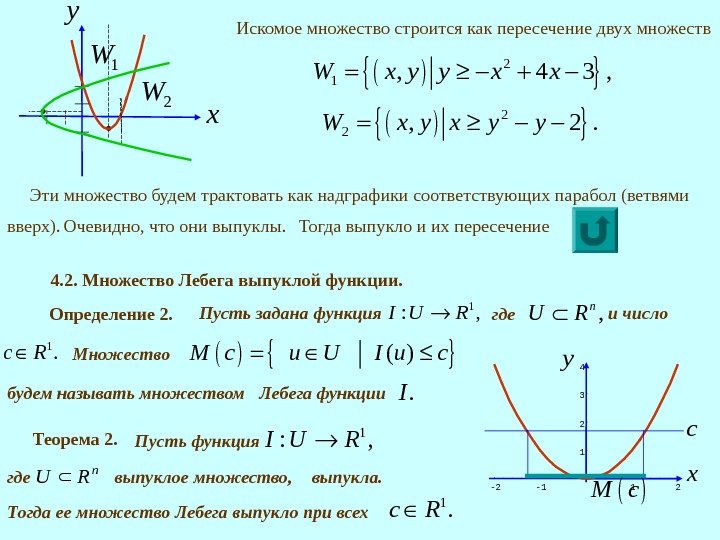
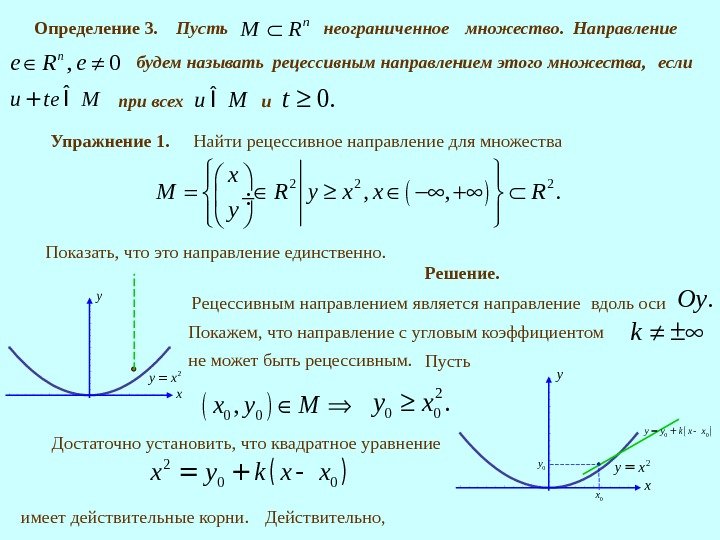
Искомое множество строится как пересечение двух множеств 2 1, 4 3 , W x y y x x 2 2, 2. W x y y Эти множество будем трактовать как надграфики соответствующих парабол (ветвями вверх). Очевидно, что они выпуклы. Тогда выпукло и их пересечение 4. 2. Множество Лебега выпуклой функции. Определение 2. Пусть задана функция 1: , I U R где , n. U R и число 1. с R Множество ( )М c u U I u c будем называть множеством Лебега функции . I Теорема 2. Пусть функция 1 : , I U R где n. RU выпуклое множество, выпукла. Тогда ее множество Лебега выпукло при всех 1. с R -2 -1 1 21234 c x y M c x y 1 W 2 W

Доказательство. Для любых 1 2, u u M c и 1, 0 из выпуклости функции I и определения множества Лебега выводим 1. c c c 1 2 1 I u u Таким образом, 1 21. u u M c Теорема доказана. 1 2( ) 1 ( ) c c I u Заметим, что обратное утверждение неверно: 1 Rc из выпуклости множеств Лебега при всех вообще говоря, не следует выпуклость функции. I Например, функция 13 , )( Ruuu. I не является выпуклой, а множества Лебега для нее 1. c R выпуклы при всех 3, M c c Заметим, что эти множества неограниченны. -2 -1 1 2 -0. 15 -0. 1 -0. 05 0. 15 x y c M c Выведем условия, когда множества Лебега ограничены при всех 1. c R Для этого уточним некоторые свойства неограниченных множеств.

Определение 3. Пусть n. M R неограниченное множество. Направление , 0 n e R e будем называть рецессивным направлением этого множества, если u te M+ Î при всех u MÎ и 0. t y x 2 y x= Упражнение 1. 2 2 2 , , . x M R y x x R y Найти рецессивное направление для множества Показать, что это направление единственно. Решение. Рецессивным направлением является направление вдоль оси. Oy y x 2 y x=0 y 0 x ()0 0 y y k x x= + — Пусть 0 0, x y M 2 0 0. y x. Покажем, что направление с угловым коэффициентом k не может быть рецессивным. Достаточно установить, что квадратное уравнение () 2 0 0 x y k x x= + — имеет действительные корни. Действительно,

() 2 0 0 x y k x x= + — ÞДискриминант этого уравнения () 2 02 2 0 04 4 4 x D k kx y ³ = — — = — + ³ 2 2 0 04 4 k kx x- + = () 2 02 0 k x= — ³ Þ 0. D³ y x 2 y x=0 y 0 x ()0 0 y y k x x= + — Установлено, что для любой точки 0 0, x y M направление с любым угловым коэффициентом k пересекает границы множества. M Покажем, что не всякое неограниченное множество имеет рецессивные направления. y x 2 y x= 22 y x= 0 y 0 x ()0 0 y y k x x= + — Действительно, множество 2 2. nx M R x y x R y является таковым. 2 0 00 x kx kx y- + — =В случае 0 D = Þ 2 0 0 0, 2. y x k x= = Секущая превращается в касательную и не является рецессивным направлением.

Лемма 1. Замкнутое неограниченное выпуклое множество Доказательство. Из неограниченности множества M , 1, 2, ku M kÎ =L такой, что. ku Пусть . u MÎ Полагаем k k k u u e u u рецессивное направление. имеет хотя бы одно следует существование последовательности {}, ku Не теряя общности, будем считать, что , 1. ke e e Для произвольного 0 t в силу kuk для достаточно больших номеров справедливо неравенство 0 1. k t u u Тогда из выпуклости множества M имеем для достаточно больших номеров k } k ku u k u u u t e- -+ = k k u u u t u u — + = — [] () 0, 1 k k t u u u a= Î + — = -6447 448 1, 1, 2, ke k L

()1 ku u Ma a= + — Î Þ()ku u ua= + — В последнем соотношении перейдем к пределу при . k В силу замкнутости M множества получим, 0. u te M t+ Î ³. e ku t e M ® + Î Покажем, что для направления e включение , 0 u te M t+ Î ³ выполняется. u MÎ для всех точек Действительно по доказанному, , 0. u e Mm m+ × Î ³ Пусть число 0 столь велико, 0, 1. t что имеет место Из выпуклости множества M для произвольной точки u M следует включение [] () 0, 1 k k t u u u a Î = + — = — [] () [] 0, 1 1 M M M t t u e u m m m Î Î Îæ ö ÷ ç ÷ ç + + — = ÷ ç ÷ ç è ø 6444447 444448 u te t u ut m m + + — = ()ku te+

()(). 1 t u te u u. M m -Î+ +Устремляя в бесконечность, M с учетом замкнутости множества в пределе из (1) получим Теорема 3. Пусть 1: RRIn выпуклая функция. при котором множество a. M ограниченно. Доказательство. Пусть множество a. M ограниченно. Остается рассмотреть лишь случай . c a Для ограниченности множеств n Rc. M достаточно существования хотя бы одного числа 1 , a R множество M c неограниченно. при любых значениях 1 Rc. Лемма доказана. множество замкнуто, это ( ). М c u U I u a М a Для c a справедливо включение Предположим, что при некотором ac значении непрерывности выпуклой функции I Заметим, что в силу а по теореме 2 и выпукло. u tet t u u m m= + + — =. u te M + Î

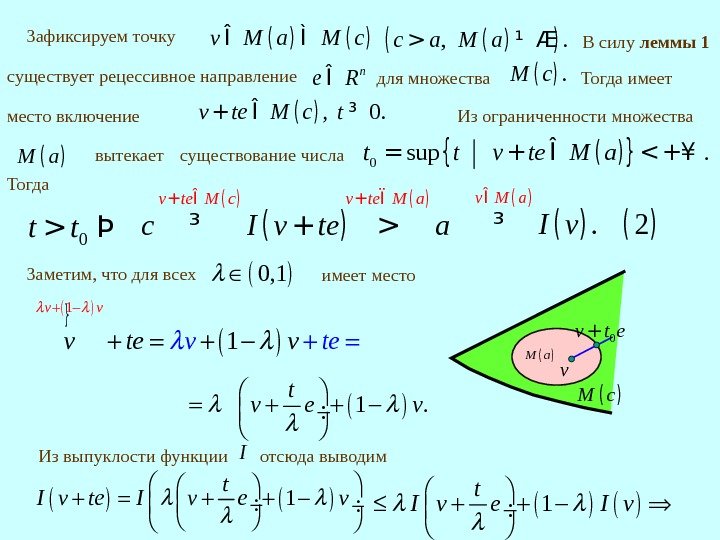
Зафиксируем точку ()(), . c a M a> ¹ Æ Из ограниченности множества ()M a вытекает существование числа (){}0 sup. t t v te M a= + Î () ()(). 2 v M a I v Î ³ 0 t t> Þ 0, 1 имеет место В силу леммы 1 ()()v M a M cÎ Ì ()M a ()M c v 0 v t e+ существует рецессивное направление n e RÎ для множества(). M c (), 0. v te M c t+ Î ³ место включение Тогда имеет

I v te I v It I v e v }. 3 v te M a I v te av M a I v te I vt I v e I v 6 7 8 В (3) устремим 0, 1 0. В силу неравенства (2) 2 I v te I v получим . t I v e 1 t I v e. I v te I v 0 3 0 I v te I v 6 4 4 7 4 48 ()M a ()M c v 0 v t e+ Тогда найдется число 0, 1 00, что t I v e c при всех 00, . имеем () t v e M c l + Î Þ()0, 1. t I v e cl l æ ö ÷ç+ £÷ç÷çè ø » ÎС другой стороны, по построению вектора e (рецессивное направление) Полученное противоречие доказывает теорему.

4. 3. Опорная функция подмножества пространства . n R Пусть n. RU компактное множество. Определение 4. 1: , n UR R Функция определенная формулой max , , , 1 n Uu U v u v v R называется опорной функцией множества . U Максимум в правой части (1) действительно достигается и непрерывности скалярного произведения. Упражнение. Вычислить опорную функцию шара ()0, . n O ReÌ Решение. Максимум в (1) достигается на векторе 0. v u v e = Тогда 2 v v e = Упражнение. Вычислить опорную функцию квадрата 1 2 20, 1 1, 1. u K u R u u u множества U в силу компактности (), U v vc e = =. ve ()0, Oe 0 u v e u

Решение. 1 2 1 1 2 2 1 1 max u u u v max , U u Uv u v 1 2. v v 1 2 1 1 2 2 1, 1 max u u u v 0, 1 K v 0 u u 1 1 1, 0, 0, 1, 0 v u v v v 1 2 1 1 2 2 , 0, 0, 0, , 0 v v v 6 4 4 7 4 4 8 2 2 2 1, 0, 0, 1, 0 v u v v v

Свойство 1. Опорная функция является положительно однородной. Доказательство. max , Uv u U u v 6 4 7 48 , , 0. n Uv v R 0 0 max , Uu U v u v Свойство 2. Для любых n Rvv 21, справедливо неравенство 1 2. U U Uv v Доказательство. 1 2. U Uv v 1 2 max , U u Uv v u v v 1 2 max , U U v v u Uu v 6 4 7 48 6 4 7 4 8 Свойство 3. Опорная функция является выпуклой функцией. Доказательство. По свойству 1 и 2 имеем свойст 1 во 1 21 , , , 0, 1. n U Uv v R свойство 2 свойство 1 1 21 1 U U Uv v

Свойство 4. Пусть , . n. U W R Тогда . U Wv v v Доказательство. , max , u U w Wu w v max , U Wz U w W u v z v max , U Wv w W v u U u v w v 64 7 48 6 4 7 48 Следствие. Справедливо равенство ()(). U U v v v ec c e = + Доказательство. ()()0, UOU v v veec c c= + = ()0, U U O ee= + Þ , max , , u U w W u v w v . U Wv v (). Uv vc e+

Пример 3. Вычислить опорную функцию шара 0, . n. O u R R Решение. В силу представления ROu. Ru. O, 0, 00 и свойства 4 опорной функции находим 0 0 , 1 0 : , u. O R u vпример R v v v 64 7 48 0 0, 0, O u R u O Rv v Пусть A квадратная матрица n го порядка. Полагаем. AU v Au u U Свойство 5. Справедливо равенство . T AU Uv A v Доказательство. () max , AU z Au AUv z vc Î= = max , T u U u A v Î = Следствие 1. Имеет место равенство . U Uv v Доказательство. Вытекает из свойства 5 при . A E 0 , . u v R v max , u U Au v Î = ()(). 2 T UA vc Действительно, 5 свойст E U во Uv v T UE v . Uv

Доказательство. Вытекает из предыдущего следствия и свойства 1. Свойство 6. Пусть , , n. U W R U W компактные множества. , . n U Wv v v R max , , . n Ww W w v v v R Доказательство. max , Uu U U Wv u v Тогда Следствие 2. Опорная функция является положительно однородной по аргументу , n U R т. е. , 0. U Uv v Действительно, 0 следствие 1 10 =U U свойство v v . Uv