ВЫПУКЛЫЙ АНАЛИЗ ЛЕКЦИЯ 1 n R 1. ПРОСРАНСТВО

ВЫПУКЛЫЙ АНАЛИЗ ЛЕКЦИЯ 1 n R 1. ПРОСРАНСТВО ПОДМНОЖЕСТВ

ЛИТЕРАТУРА 1. Благодатских В. И. Введение в оптимальное управление, М. Высшая школа 2001. 2. Васильев Ф. П. Численные методы решения экстремальных задач, М. : Наука, 1988. 3. Рокафеллер Р. Выпуклый анализ, М. : Мир, 1973. 4. Пшеничный Б. Н. Выпуклый анализ и экстремальные задачи, М. : Наука, 1979. 6. Лутманов С. В. Курс лекций по методам оптимизации. Ижевск, РХД, 20015. Алексеев В. М. , Тихомиров В. М. , Фомин С. В. Оптимальное управление, М. : Наука, 1979.

1. ПРОСРАНСТВО ПОДМНОЖЕСТВ. n R 1. 1. Пространство . n R 1. 2. Точки и подмножества пространства . n R

1. ПРОСРАНСТВО ПОДМНОЖЕСТВ. n R 1. 1. Пространство . n R Рассмотрим n мерное евклидово векторное пространство n R с элементами 1. n u u u L В частности 1 R числовая ось, 2 R — двухмерная плоскость и т. д. При этом будем различать одноточечные множества и В первом случае это будет , nu R а во втором. n u R n R будем обозначать строчными буквами, Элементы n R а подмножества заглавными. В пространстве n R определены операции: сложения векторов 1 1 n nu v L L. n Rточку этого множества, как элемент 1 1 ; n nu v L u v

, u vумножение вектора на число скалярное произведение векторов u Это пространство является нормированным с нормой , u u u 2 1. n i i u Норма определяет расстояние между любыми двумя точками пространства n R по формуле , u v 2 1. n i i i u v 1 n u u L 1. n i i i u v 1 ; n u u L

1. 2. Точки и подмножества пространства Открытой окрестностью точки n Ru 0 называется множество Множество 0, O u R. n R По отношению к произвольному множеству n RU внутренние, Определение 1. 0, 0. n u R R 0 0, , n. O u R u u R внешние, граничные и изолированные. 0 u. R 0 uеще называют открытым шаром с центром в и радиуса . R точке Множество 0, 0. n u R R 0 0, , n. O u R u u R называют замкнутой окрестностью точки 0. n u R можно определить следующих четырех типов: точки 0 u. R

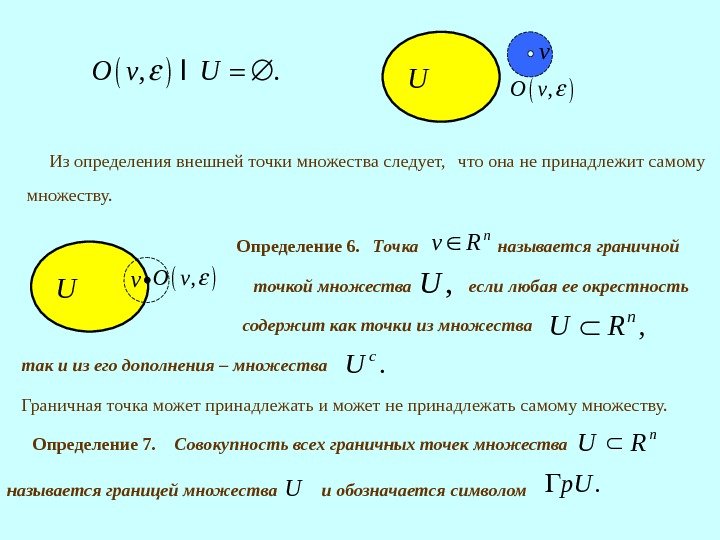
v. Точка называется внутренней точкой множества , U если , O v U для некоторого 0. Uv , O v Совокупность всех внутренних точек множества U называется внутренностью множества U и обозначается символом int. U Очевидно, что если внутренность множества не пуста, то она открыта. Например, плоский диск в трехмерном пространстве не имеет внутренних точек. Множество состоящее только из внутренних точек Точка n Rv называется внешней по отношению к множеству n RU , если Uv и для некоторого 0 выполнено Определение 2. Определение 3. Заметим, что не любое множество имеет непустую внутренность. Определение 4. Определение 5. открытым множеством называется

, . O v U IИз определения внешней точки множества следует, v U , O v так и из его дополнения – множества . c U Точка n Rv называется граничной , U точкой множества Граничная точка может принадлежать и может не принадлежать самому множеству. если любая ее окрестность , n U R содержит как точки из множества Совокупность всех граничных точек множества n RU называется границей множества U и обозначается символом . р. UОпределение 6. Определение 7. v U, O vмножеству. что она не принадлежит самому

v U, O v. Точка n Rv называется изолированной для множества , U если Uv и существует такая окрестность , , O v что , . U O v v. I Пусть . n U R Точка u называется предельной точкой множества , U Множество n U R называется замкнутым, Это свойство позволяет ввести следующее определение. Определение 8. Определение 9. содержится хотя бы одна точка множества . Uесли в любой открытой окрестности этой точки Определение 10. Пересечение любого числа замкнутых множеств замкнуто. содержит все свои предельные точки. если оно

Замыканием U множества U называется наименьшее замкнутое множество, содержащее . U Заметим, что \ int. р. U U U Множество 0, O R не является замкнутым , Множество Кроме того, справедливо замкнуто и Определение 11. Пример 1. 0 R 0, , n O R u R 0 0, , 0 R O R L точка так как, например, 0, . O R даже является замыканием множества хотя она является предельной 0, . O R для множества 0, . O R

1) int 0, 0, ; O R 2) 0, 0, р O R S R Множество n RU называется ограниченным, Множество n RU называется компактным, сходящуюся к некоторому элементу этого множества. Определение 12. Определение 13. Напомним, что из последовательности элементов компактного множествазамкнуто и ограничено. если оно 0. n s R s u R можно извлечь подпоследовательность, всегдасодержится в замкнутом шаре если оно конечного радиуса. 0, O RU 0, O R

Прямая на плоскости не является компактным множеством, Пусть n RU компактное множество. Величина u. U Uu max называется модулем множества . U В силу непрерывности функции нормы Таким образом, 0, . U O UПример 2. Множество 0, O u r компактно. Множество 0, O R не является компактным, т. к. оно не замкнутое. Определение 14. U и компактности множества операция max в принятом определении корректна. Геометрический смысл модуля множества таков: содержащего это множество. т. к. это неограниченное множество. U U O это есть радиус наименьшего шара с центром в начале координат,

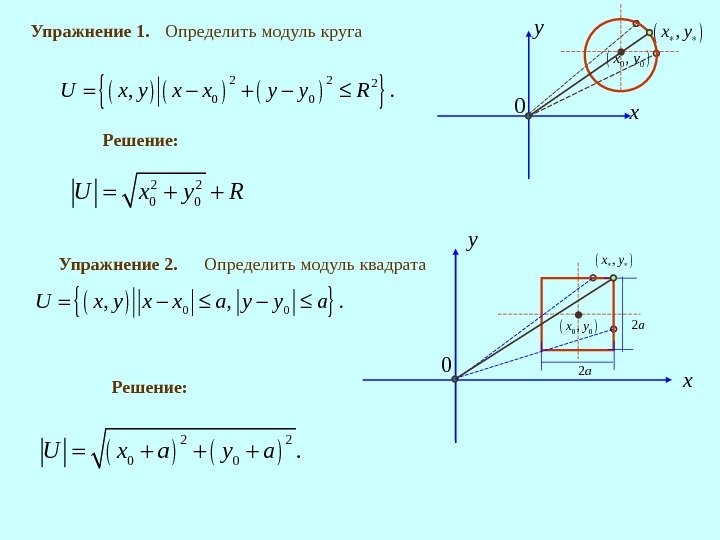
Упражнение 1. Решение: Определить модуль круга 2 22 0 0, . U x y x x y y R 2 2 0 0 U x y R Упражнение 2. Определить модуль квадрата 0 0, , . U x y x x a y y a Решение: x y 0 0 0, x y 2 a 2 a 2 2 0 0. U x a y a x y 0 0 0, x y