ВВЕДЕНИЕ В ТЕРИЮ ЦЕПЕЙ МАРКОВА И ЕЕ ИНЖЕНЕРНЫЕ

ВВЕДЕНИЕ В ТЕРИЮ ЦЕПЕЙ МАРКОВА И ЕЕ ИНЖЕНЕРНЫЕ ПРИЛОЖЕНИЯ Мизонов Вадим Евгеньевич КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ИГЭУ

ЗАДАЧА О ПЬЯНОМ МАТРОСЕ 65 43 1 2 Расчетная схема блужданий пьяного матроса

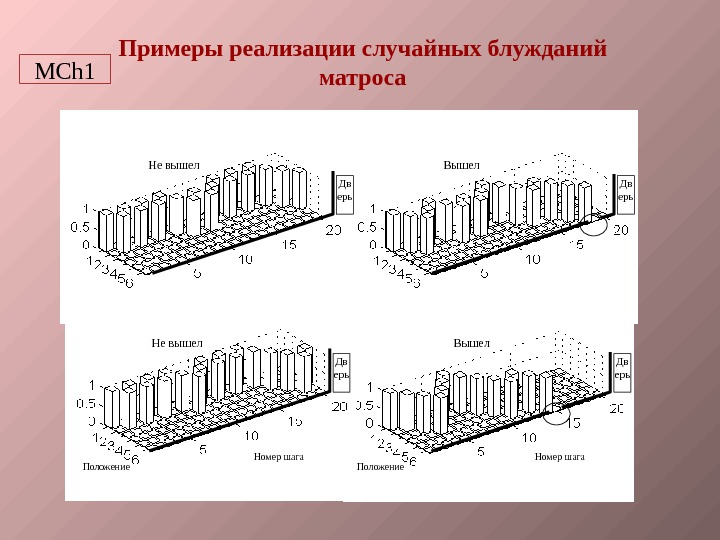
Дв ерь. Не вышел Дв ерь. Вышел Номер шага Положение Примеры реализации случайных блужданий матроса. MCh

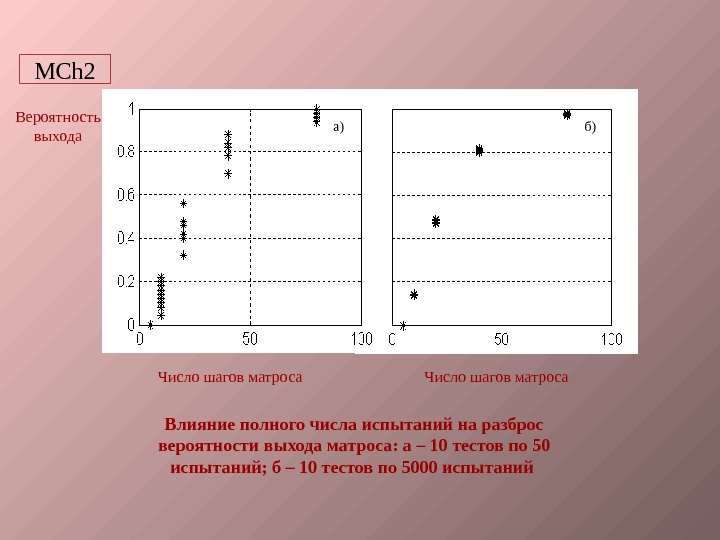
Вероятность выхода Число шагов матроса Влияние полного числа испытаний на разброс вероятности выхода матроса: а – 10 тестов по 50 испытаний; б – 10 тестов по 5000 испытаний а) б)MCh

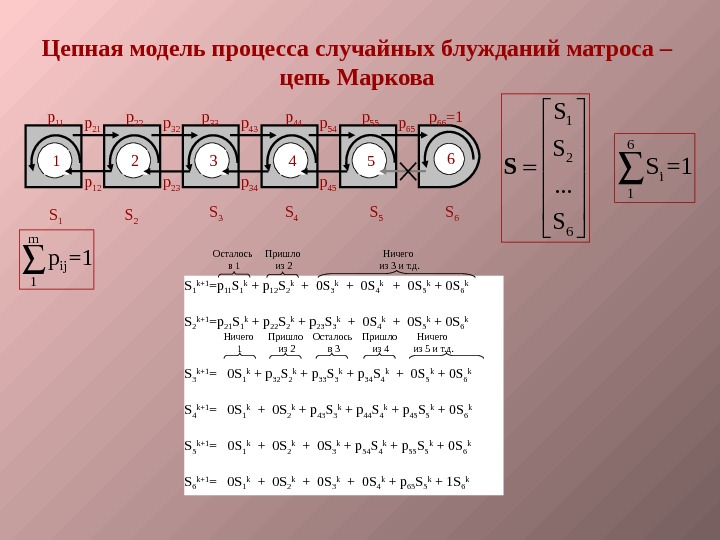
6 54321 p 12 p 11 p 32 p 23 p 22 p 65 S 1 S 2 S 3 S 4 S 5 S 6 p 43 p 54 p 44 p 33 p 55 p 34 p 45 p 66 =1 Цепная модель процесса случайных блужданий матроса – цепь Маркова 1 2 6 S S. . . S S 6 i 1 S =1 m ij 1 p =1 S 1 k+1 =p 11 S 1 k + p 12 S 2 k + 0 S 3 k + 0 S 4 k + 0 S 5 k + 0 S 6 k S 2 k+1 =p 21 S 1 k + p 22 S 2 k + p 23 S 3 k + 0 S 4 k + 0 S 5 k + 0 S 6 k S 3 k+1 = 0 S 1 k + p 32 S 2 k + p 33 S 3 k + p 34 S 4 k + 0 S 5 k + 0 S 6 k S 4 k+1 = 0 S 1 k + 0 S 2 k + p 43 S 3 k + p 44 S 4 k + p 45 S 5 k + 0 S 6 k S 5 k+1 = 0 S 1 k + 0 S 2 k + 0 S 3 k + p 54 S 4 k + p 55 S 5 k + 0 S 6 k+1 = 0 S 1 k + 0 S 2 k + 0 S 3 k + 0 S 4 k + p 65 S 5 k + 1 S 6 k. Пришло из 2 Осталось в 1 Ничего из 3 и т. д. Пришло из 2 Осталось в 3 Ничего из 5 и т. д. Пришло из 4 Ничего

k+1 k 11 12 1 1 k+1 k 21 22 23 2 2 k+1 k 32 33 34 3 3 k+1 k 43 44 45 4 4 k+1 k 54 55 5 5 k+1 k 65 6 6 p p 0 0 S S p p p 0 0 0 S S 0 p p p 0 0 S S = 0 0 p p p 0 S S 0 0 0 0 p 1 S S 0 0, 5 0 0 1 0 0, 5 0 0 0 0 0, 5 1 P S k+1 =PS k Матричная запись q k = S 5 k p 65 = S 6 k +1 — S 6 k k 1 = kq

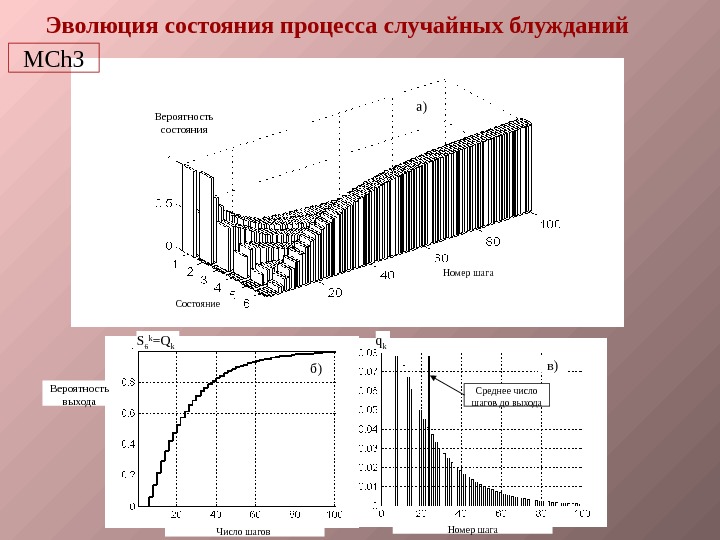
а) Номер шага Состояние. Вероятность состояния. Эволюция состояния процесса случайных блужданий Число шагов Номер шага. Вероятность выхода б) в) Среднее число шагов до выходаq k. S 6 k =Q k. MCh

Начальный момент. Вещество локализовано Время пошло. Вещество диффундирует Продолжение диффузии Вещество распределилось равномерно Капля вещества Иллюстрация процесса диффузии Одномерная диффузия. Виды и влияние краевых условий d Δc q =-D Δx 2 2 c c =D t x 2 d p 12 =d p 32 =d+vp 22 =1 -2 d-v v Выделение симметричной составляющей вероятностей перехода f f 1 -d-v d 0 0 0 0 d+v 1 -2 d-v d 0 0 = 0 0 d+v 1 -2 d-v d 0 0 d+v 1 -d-v 0 0 0 v 1 P — Матрица диффузии: 2 Δt d=D Δx Δt v=V Δx

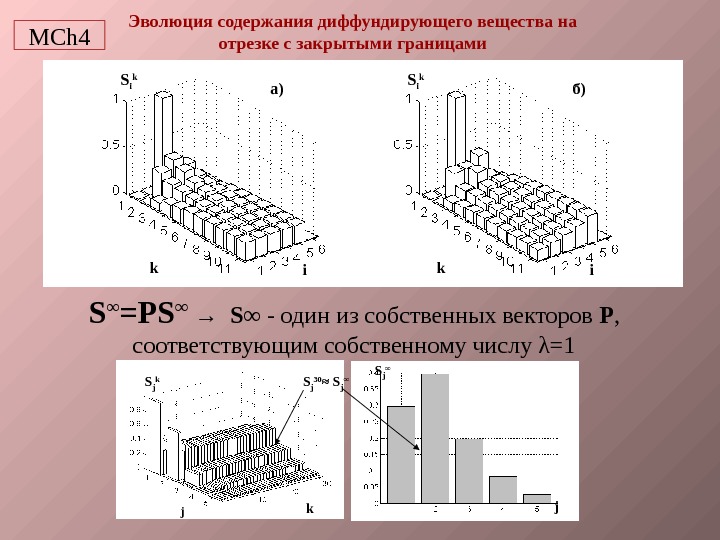
Эволюция содержания диффундирующего вещества на отрезке с закрытыми границами S i k k i а) б) S ∞ =Р S ∞ → S ∞ — один из собственных векторов Р , соответствующим собственному числу λ=1 S j k S j 30 ≈ S j ∞ k j j. MCh

Диффузия с источниками или процесс с порождением частиц S k+1 =PS k +S f k – вектор подачи q k inq k in q k out k k. MCh

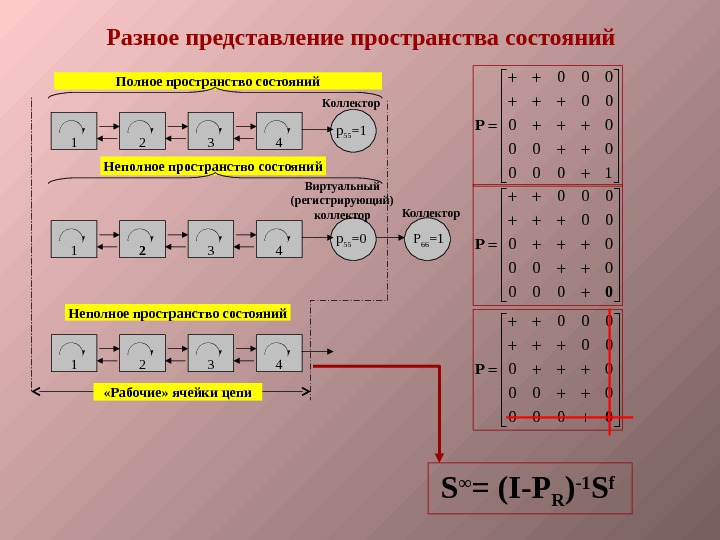
1 2 3 4 Коллектор p 55 =1 1 2 3 4 Виртуальный (регистрирующий) коллектор p 55 =0 1 2 3 4 P 66 =1 Коллектор «Рабочие» ячейки цепи Полное пространство состояний Неполное пространство состояний Разное представление пространства состояний S ∞ = (I-P R ) -1 S f 0 0 0 0 1 P 0 0 0 0 0 0 0 P

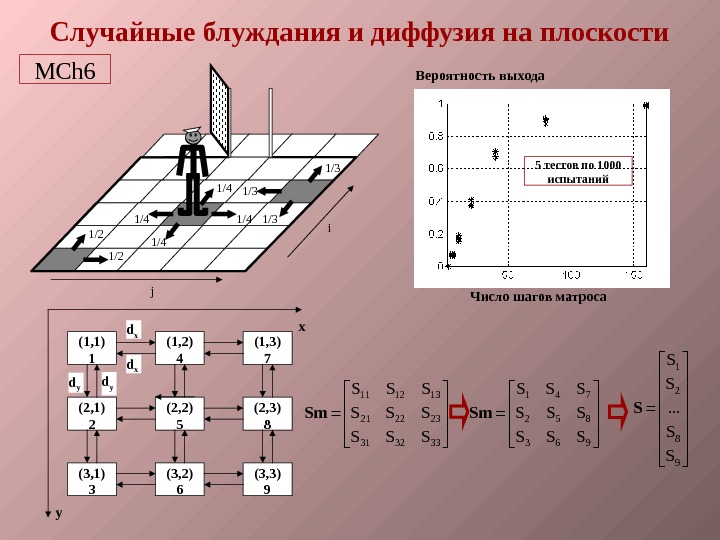
Случайные блуждания и диффузия на плоскости 1/2 1/41/4 1/31/3 i j 5 тестов по 1000 испытаний Число шагов матроса Вероятность выхода (1, 1) 1 (1, 2) 4 (1, 3) 7 (2, 1) 2 (2, 2) 5 (3, 1) 3 (3, 2) 6 (3, 3) 9(2, 3) 8 x y d x d yd y 11 12 13 21 22 23 31 32 33 S S S S S Sm 1 4 7 2 5 8 3 6 9 S S S S S Sm 1 2 8 9 S S. . . S S SMCh

1 1 2 1 0 4 1 0 0 0 1 2 2 2 3 2 0 5 1 0 0 0 2 3 3 3 0 0 6 3 0 0 0 1 4 0 0 4 4 5 4 0 7 4 0 0 0 2 5 0 4 5 5 5 6 5 0 8 5 0 0 0 3 6 0 5 6 6 6 0 0 9 6 0 0 0 4 7 0 0 7 7 8 7 0 0 0 5 8 0 7 8 8 8 9 8 0 0 0 6 9 0 8 9 9 9 P 1 2 0 0 0 1 3 0 0 0 1 2 0 0 0 0 1 3 0 0 0 1 4 0 0 0 1 3 0 0 0 0 1 2 0 0 0 1 3 0 0 0 1 d d d d d d d d d P 11 12 21 22 23 32 33 P P Z P PСтруктура переходной матрицы

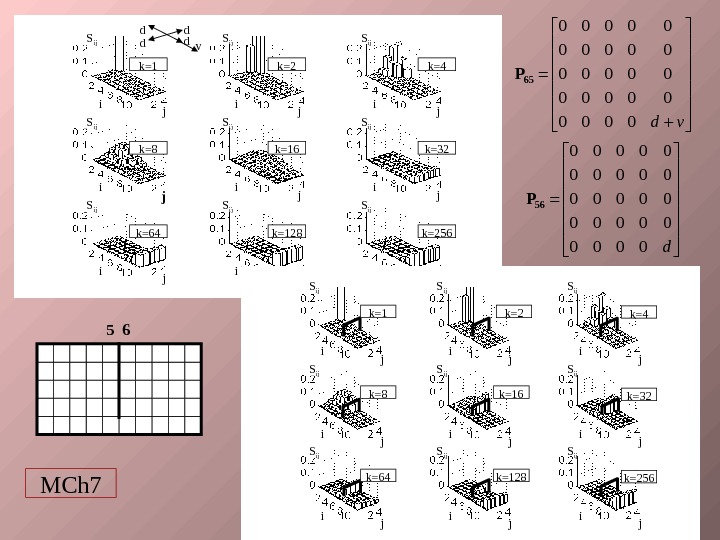
d dd d v i. S ij i i. S ij j j jk=1 k=2 k=4 i. S ij i i. S ij j j jk=8 k=16 k=32 i. S ij i i. S ij j j jk=64 k=128 k=2560 0 0 0 0 0 d v 65 P 0 0 0 0 0 0 d 56 P 5 6 MCh

Конец лекции 1 Спасибо за внимание

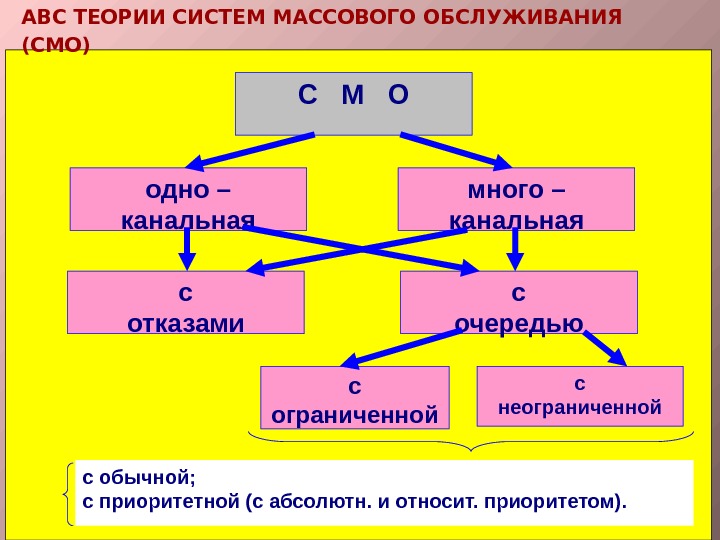
С М О с неограниченнойс ограниченной с очередьюс отказами много – канальнаяодно – канальная с обычной; с приоритетной (с абсолютн. и относит. приоритетом). ABC ТЕОРИИ СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ (СМО)

окончание ремонта работа ремонт работа состояниеотказ переход (событие) — событие: сис-ма пере- ходит из состояния i в состояние j; t + ∆tt t ttt 1 2 3 4 t 1 t 2 8 7 79 P I J (t) – поток событий; λ I J = P I J (t, ∆t)/ ∆t – интен- сивность потока событий (плотность вероятности перехода. Стационарный случайный процесс λ I J = const. ПОТОКИ СОБЫТИЙ

событие=окончание ремонта ( μ )событие=отказ ( ν ) Состояние 1 ( работает ) Вероятность S 1 Состояние 2 ( ремонтируется ) Вероятность S 2 N систем: NS 1 — работает, NS 2 — не работает (в ремонте) уходит из 1 : NS 1 ν В ед. времени NS 1 ν = NS 2 μ приходит в 1 : NS 2 μ S 1 + S 2 = 1 Доход Д = Д 0 S 1 = μ /( μ + ν ) 1 / 2 1 / 3 2 / 3 ν = μ ν = 2 μ ν = 0, 5 μ S 2 = ν /( μ + ν ) 1 / 2 2 / 3 1 / 3 ПОТОКИ СОБЫТИЙ И ВЕРОЯТНОСТИ СОСТОЯНИЯ

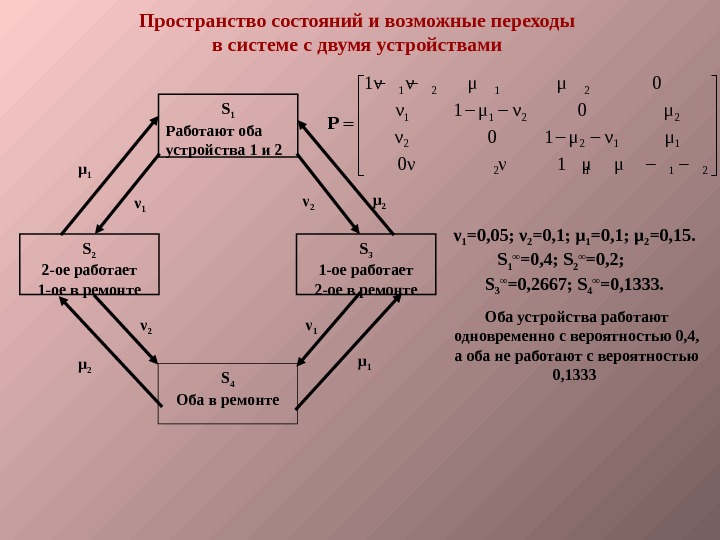
S 1 Работают оба устройства 1 и 2 S 2 2 -ое работает 1 -ое в ремонте S 3 1 -ое работает 2 -ое в ремонте S 4 Оба в ремонтеμ 1 ν 2 μ 2 ν 1 μ 1ν 2 μ 2 Пространство состояний и возможные переходы в системе с двумя устройствами 1 2 1 1 21 ν ν μ μ 0 ν 1 μ ν 0 1 μ ν μ 0 ν ν 1 μ μ P ν 1 =0, 05; ν 2 =0, 1; μ 1 =0, 1; μ 2 =0, 15. S 1 ∞ =0, 4; S 2 ∞ =0, 2; S 3 ∞ =0, 2667; S 4 ∞ =0, 1333. Оба устройства работают одновременно с вероятностью 0, 4, а оба не работают с вероятностью 0,

Многоканальная СМО с отказами ν νν μ 2μ 3μS 1 3 свобод. 0 заняты S 2 2 свобод. 1 заняты S 3 1 свобод. 2 заняты S 4 0 свобод. 3 заняты ОТКАЗ! Потому что все равно, какой канал освободится, а их 2 ν — интенсивность потока заявок (1/ν – время чередования заявок), μ – интенсивность потока обслуживания (1/μ – время обслуживания одной заявки). 1 -ν μ 0 0 ν 1 -ν-μ 2μ 0 = 0ν 1 -ν-2μ 3μ 0 0ν 1 -ν-3μ P

S i S i S ii i 3 канала 4 канала 5 каналов 6 каналов (ν=0, 15; μ=0, 05) i i Число каналов 3 4 6 Вероятность отказа 0, 35 0, 21 0, 06 Вероятность обслуживания 0, 65 0, 79 0, 94 Доля занятых каналов 0, 65 0, 60 0, 47 S S =1– S R S S ν — интенсивность потока обслуженных заявок. Каждый занятый канал обслуживает в единицу времени μ заявок. S S ν /μ или (1– S N +1 ) ν /μ – число занятых каналов Доля занятых каналов – поделить на их общее число N.

Одноканальная СМО с очередью S 1 Свобод. Очер. =0 S 2 Занят Очер. =0 S 3 Занят Очер. =1 S 4 Занят Очер. =2 S 5 Занят Очер. =3 Мест нет!ν μ ν μ 1 — ν μ 0 0 0 ν 1 -ν-μ μ 0 0 = 0 ν 1 -ν-μ μ 0 0 0 ν 1 -μ Pm L k+2 k=1 N = k. S среднее число заявок в очереди m k+2 Lk=1 L k. S N T = = ν ν среднее время стояния заявки в очереди N L =2, 2 ; T L = 4, 4 ед. вр. N L =5; T L = 1 0 ед. вр. S i i i

Номер состояния: 1 2 3 4 5 Сумма у игрока $0 $1 $2 $3 $4 S i k k i p=0, 5 i. S i ∞ S i k k i p=0, 25 i. S i ∞ S i k k i p=0, 75 i. S i ∞

Разные задачи Пенсионные отчисления Неработающие дети (1), работающие взрослые (2), пенсионеры (3) и умершие (4). Пусть каждый год 0, 04 детей становятся работающими взрослыми, а 0, 001 умирают; 0, 03 работающих взрослых уходят на пенсию, а 0, 01 умирают; умирает также 0, 05 пенсионеров. Найти установившееся число жителей в группах, если в год рождается 1000 детей. 0, 959 0 0, 04 0, 96 0 0, 03 0, 95 0 0, 001 0, 05 1 P Пришло Ушло 1000 = (0, 04+0, 001) N 1 (дети) 0, 04 N 1 =(0, 03+0, 01) N 2 (работающие взрослые) 0, 03 N 2 =0, 05 N 3 (пенсионеры) N 1 =24390; N 2 =24390, 24; N 3 =14634, 14 Пусть пенсия у пенсионеров составляет $ 5000 в год и формируется из отчислений дохода работающий взрослых. Годовые пенсионные отчисления с работающих 5000 *14634, 14/24390, 24=$ 3000 в год с каждого

Конец лекции 2 Спасибо за внимание