Временные ряды в эконометрических исследованиях 1. Специфика временного





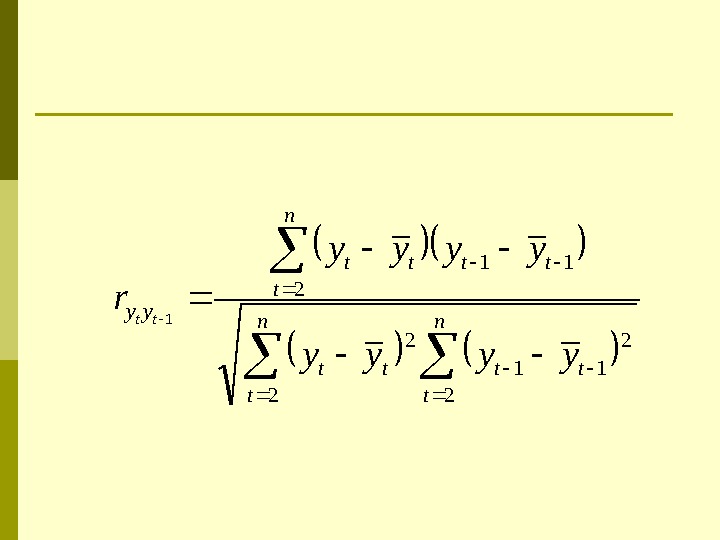





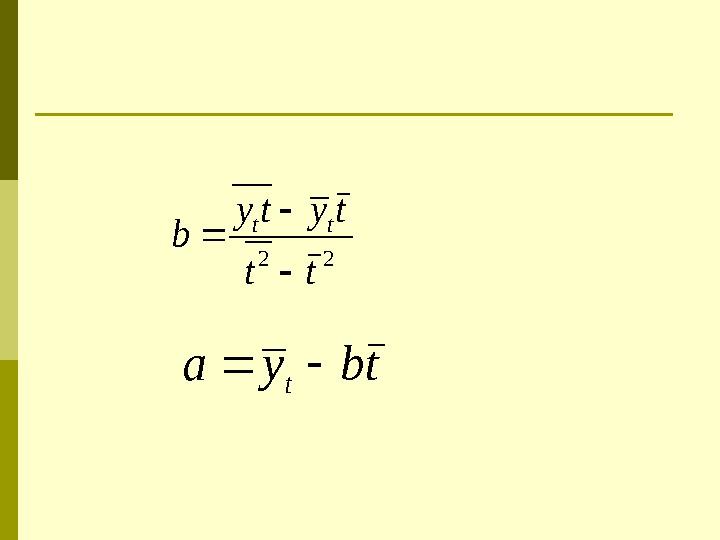
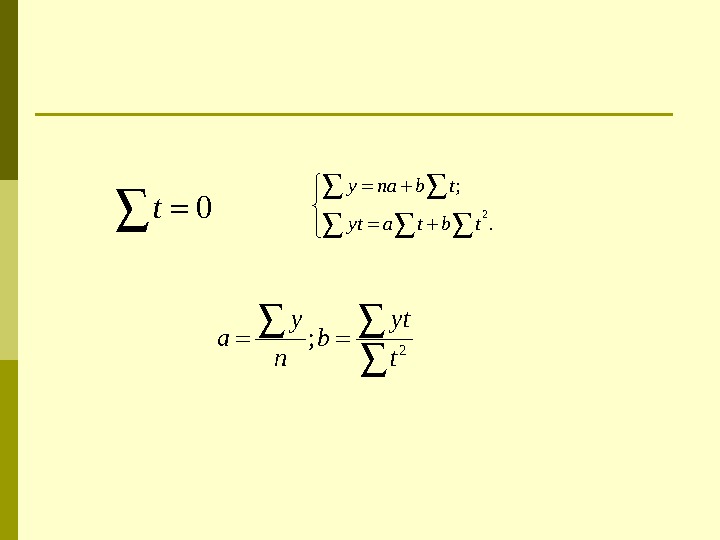

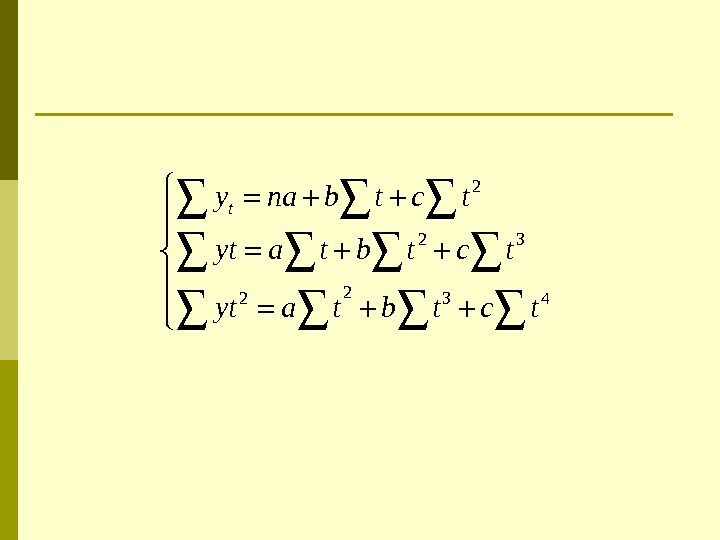

tema_4_vremennye_ryady_2010-2011_1_chasty.ppt
- Размер: 589.5 Кб
- Автор:
- Количество слайдов: 24
Описание презентации Временные ряды в эконометрических исследованиях 1. Специфика временного по слайдам
 Временные ряды в эконометрических исследованиях 1. Специфика временного ряда как источника данных в эконометрическом моделировании. 2. Автокорреляция уровней ряда и ее последствия. 3. Моделирование тенденций временного ряда. 4. Использование трендовых моделей для прогнозирования. 5. Методы исключения тенденции при моделировании взаимосвязей по временным рядам. 6. Автокорреляция в остатках. Критерий Дарбина-Уотсона. 7. Модели с лаговыми переменными. 8. Сезонные колебания их учет при построении эконометрических моделей.
Временные ряды в эконометрических исследованиях 1. Специфика временного ряда как источника данных в эконометрическом моделировании. 2. Автокорреляция уровней ряда и ее последствия. 3. Моделирование тенденций временного ряда. 4. Использование трендовых моделей для прогнозирования. 5. Методы исключения тенденции при моделировании взаимосвязей по временным рядам. 6. Автокорреляция в остатках. Критерий Дарбина-Уотсона. 7. Модели с лаговыми переменными. 8. Сезонные колебания их учет при построении эконометрических моделей.
 Временной (динамический) ряд – это ряд последовательно расположенных во времени числовых значений соответствующего показателя Элементы временного ряда : уровни ряда ( y t )- числовые значения того или иного показателя; время ( t ). Виды временных рядов : моментные , если время задано моментами; интервальные , если время задано интервалами.
Временной (динамический) ряд – это ряд последовательно расположенных во времени числовых значений соответствующего показателя Элементы временного ряда : уровни ряда ( y t )- числовые значения того или иного показателя; время ( t ). Виды временных рядов : моментные , если время задано моментами; интервальные , если время задано интервалами.
 Модели на основе рядов динамики Модели изолированного динамического ряда. Модели системы взаимосвязанных рядов динамики. Модели авторегрессии. Модели с распределенным лагом.
Модели на основе рядов динамики Модели изолированного динамического ряда. Модели системы взаимосвязанных рядов динамики. Модели авторегрессии. Модели с распределенным лагом.
 Компоненты временного ряда Тенденция ( T) Периодические колебания (P) Случайные колебания (E)
Компоненты временного ряда Тенденция ( T) Периодические колебания (P) Случайные колебания (E)
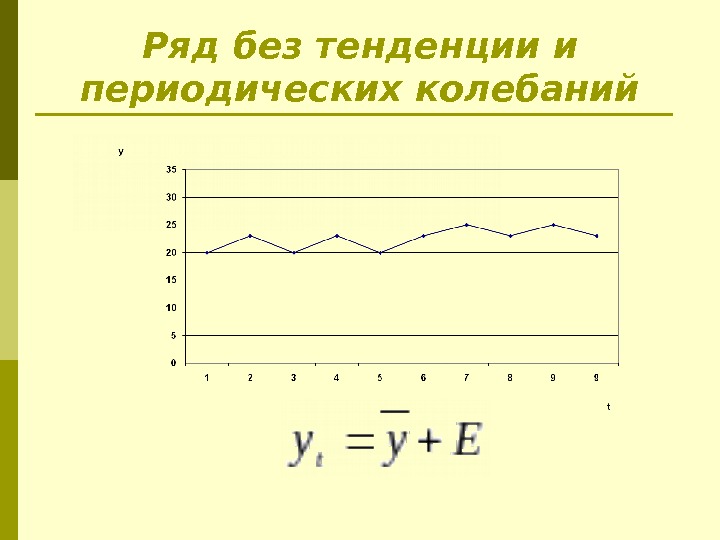
 Ряд без тенденции и периодических колебаний
Ряд без тенденции и периодических колебаний
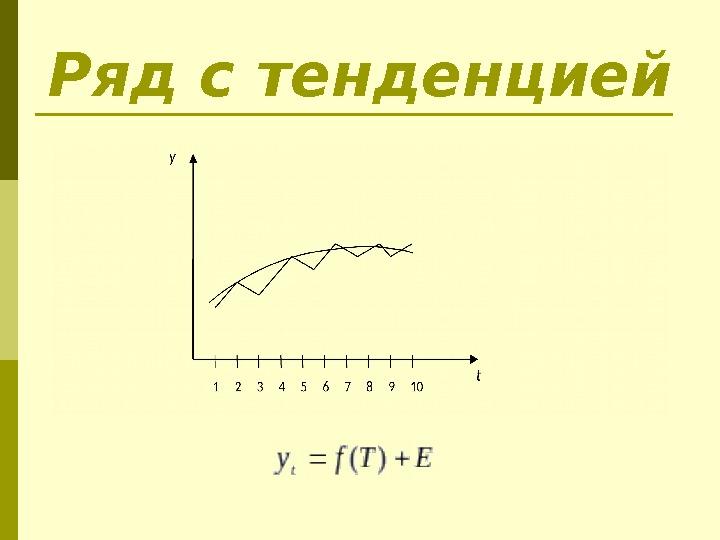
 Ряд с тенденцией
Ряд с тенденцией
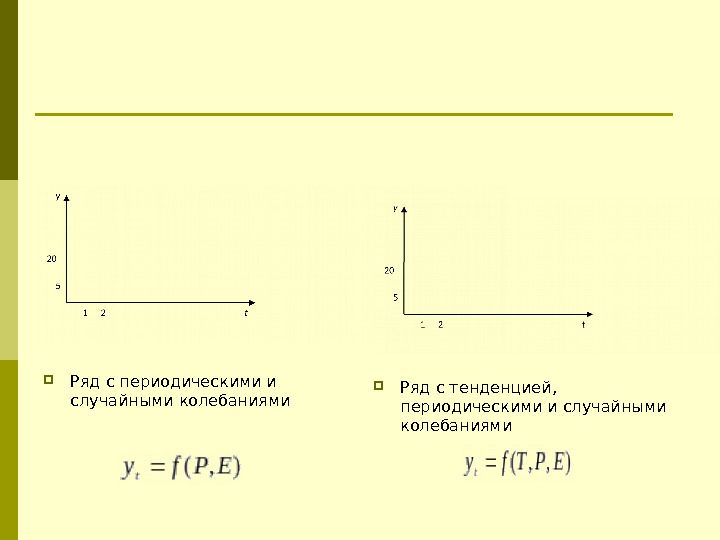
 Ряд с периодическими и случайными колебаниями Ряд с тенденцией, периодическими и случайными колебаниями
Ряд с периодическими и случайными колебаниями Ряд с тенденцией, периодическими и случайными колебаниями
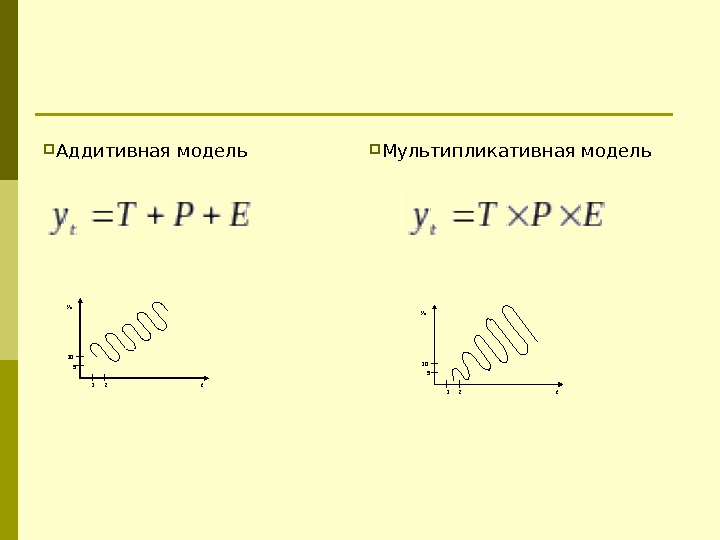
 yо t 5 10 1 2 yо t 5 10 1 2 Аддитивная модель Мультипликативная модель
yо t 5 10 1 2 yо t 5 10 1 2 Аддитивная модель Мультипликативная модель
 Автокорреляция уровней ряда и ее последствия Корреляционная зависимость между последовательными значениями уровней временного ряда называется автокорреляцией уровней ряда 1 11 1 t t t t y yy y r
Автокорреляция уровней ряда и ее последствия Корреляционная зависимость между последовательными значениями уровней временного ряда называется автокорреляцией уровней ряда 1 11 1 t t t t y yy y r
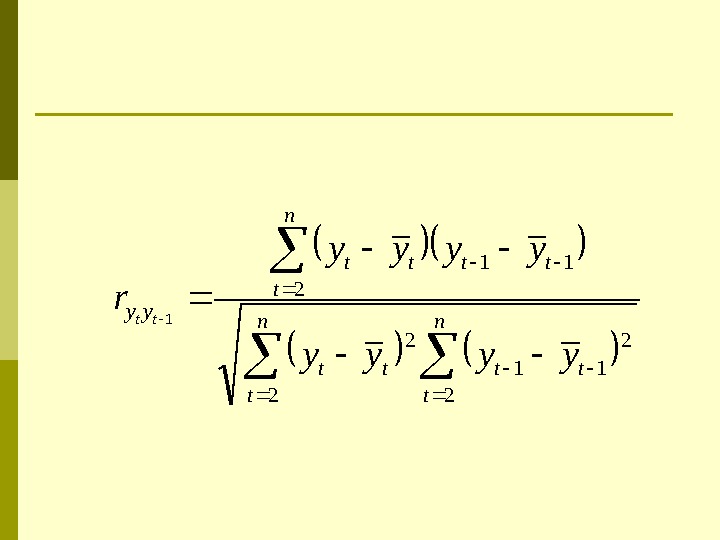 n t tttt yy yyyy r tt
n t tttt yy yyyy r tt
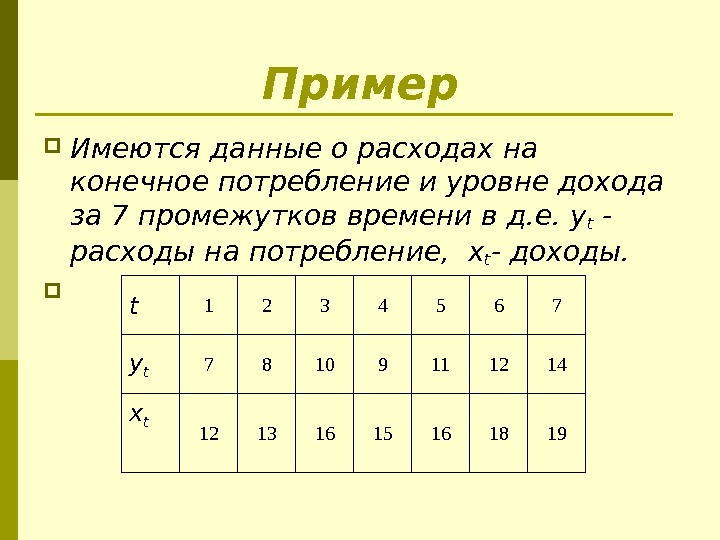
 Пример Имеются данные о расходах на конечное потребление и уровне дохода за 7 промежутков времени в д. е. yt — расходы на потребление, x t — доходы. t 1 2 3 4 5 6 7 y t 7 8 10 9 11 12 14 x t
Пример Имеются данные о расходах на конечное потребление и уровне дохода за 7 промежутков времени в д. е. yt — расходы на потребление, x t — доходы. t 1 2 3 4 5 6 7 y t 7 8 10 9 11 12 14 x t
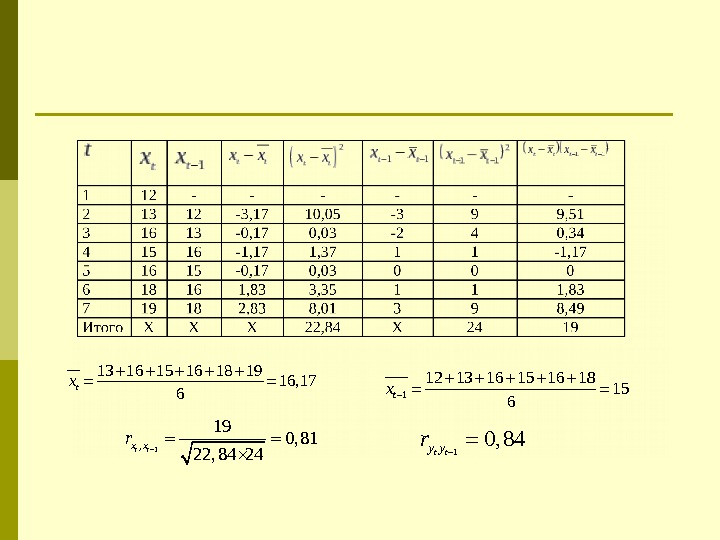
 13 16 15 16 18 19 16, 17 6 tx 1 12 13 16 15 16 18 15 6 tx 1 , 19 0, 81 22, 84 24 t t x xr 10, 84 t ty yr
13 16 15 16 18 19 16, 17 6 tx 1 12 13 16 15 16 18 15 6 tx 1 , 19 0, 81 22, 84 24 t t x xr 10, 84 t ty yr
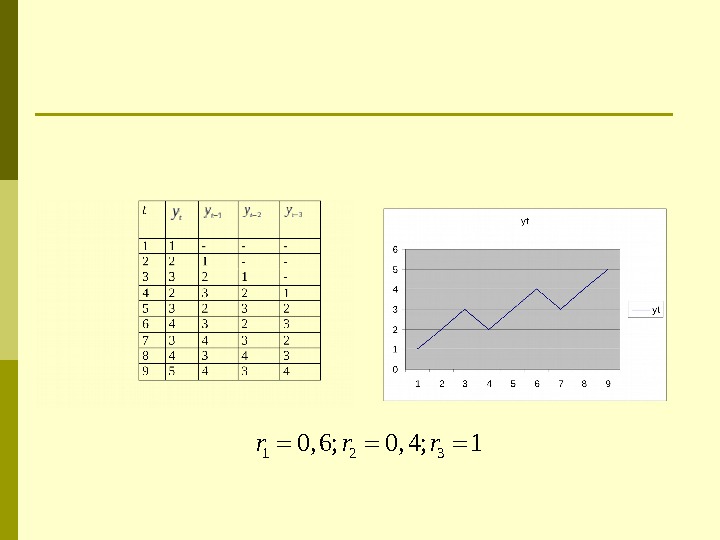
 1 2 30, 6; 0, 4; 1 r r r
1 2 30, 6; 0, 4; 1 r r r
 Моделирование тенденций временного ряда Метод аналитического выравнивания сводится к замене фактических данных сглаженными, определенными по выбранной математической функции. При этом, уровни временного ряда рассматриваются как функция от времени: tfyt
Моделирование тенденций временного ряда Метод аналитического выравнивания сводится к замене фактических данных сглаженными, определенными по выбранной математической функции. При этом, уровни временного ряда рассматриваются как функция от времени: tfyt
 Этапы построения модели тенденции (уравнения тренда) Выбор математической функции, описывающей тенденцию Оценка параметров модели Проверка адекватности выбранной функции и оценка точности модели Расчет точечного и интервального прогнозов
Этапы построения модели тенденции (уравнения тренда) Выбор математической функции, описывающей тенденцию Оценка параметров модели Проверка адекватности выбранной функции и оценка точности модели Расчет точечного и интервального прогнозов
 Виды математических функций, описывающих тенденцию Функции с монотонным характером возрастания (убывания) и отсутствием пределов роста (снижения) Кривые с насыщением, т. е. устанавливается нижняя или верхняя граница изменения уровней ряда S -образные кривые, т. е. кривые с насыщением, имеющие точку перегиба
Виды математических функций, описывающих тенденцию Функции с монотонным характером возрастания (убывания) и отсутствием пределов роста (снижения) Кривые с насыщением, т. е. устанавливается нижняя или верхняя граница изменения уровней ряда S -образные кривые, т. е. кривые с насыщением, имеющие точку перегиба
 Уравнения трендов
Уравнения трендов
 Линейный тренд y a bt
Линейный тренд y a bt
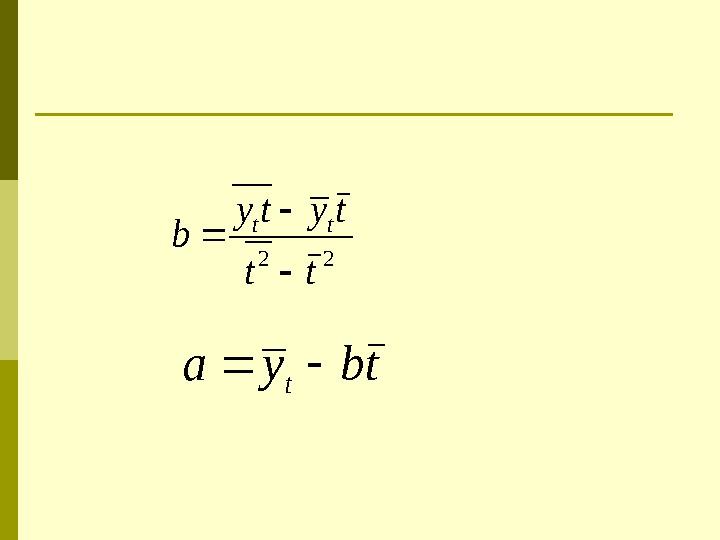 22 tt tyty b tt tbya t
22 tt tyty b tt tbya t
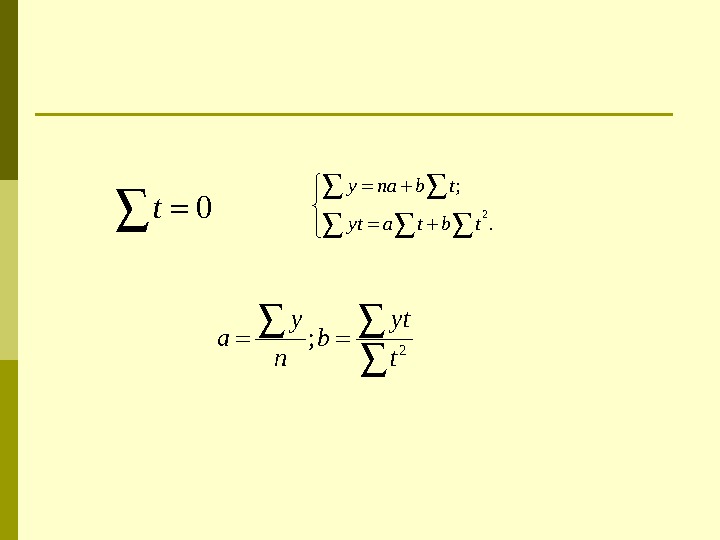 0 t 2 ; . y na b t yt a t b t 2; y yt a b n t
0 t 2 ; . y na b t yt a t b t 2; y yt a b n t
 Парабола 2 -го порядка
Парабола 2 -го порядка
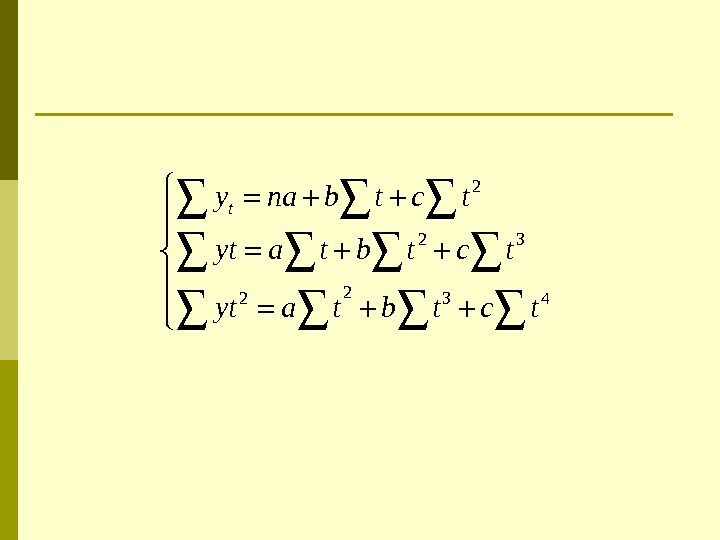 2 2 3 4 ty na b t c t yt a t b t c t
2 2 3 4 ty na b t c t yt a t b t c t
 Показательная функцияt y a b
Показательная функцияt y a b
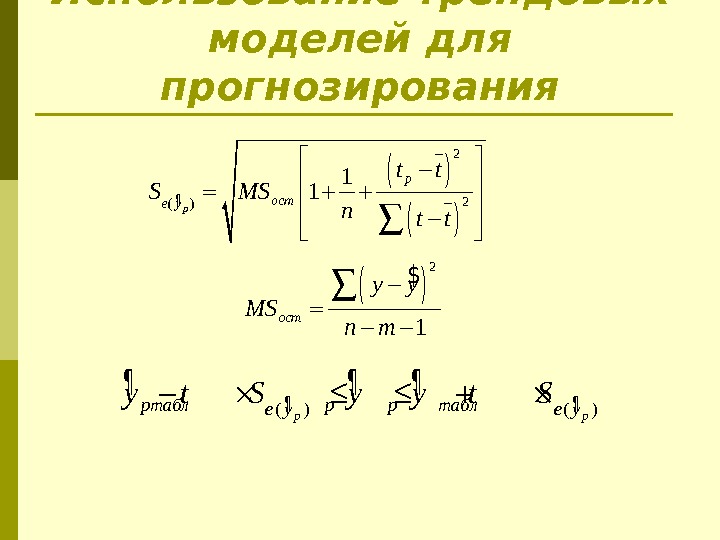
 Использование трендовых моделей для прогнозирования¶ 2 2 ( ) 1 1 p p ост e y t t S MS nt t $ 2 1 ост y y MS n m ¶ ¶ ¶¶ ¶( ) ( )p ppтабл p p таблe y y t S
Использование трендовых моделей для прогнозирования¶ 2 2 ( ) 1 1 p p ост e y t t S MS nt t $ 2 1 ост y y MS n m ¶ ¶ ¶¶ ¶( ) ( )p ppтабл p p таблe y y t S
