Устные упражнения Найдите тангенс угла наклона прямой к

Устные упражнения Найдите тангенс угла наклона прямой к положительному направлению оси абсцисс и угловой коэффициент этой прямой ху О 12 65 α Ответ : tgα = 0, 6; k = 0, 6. α

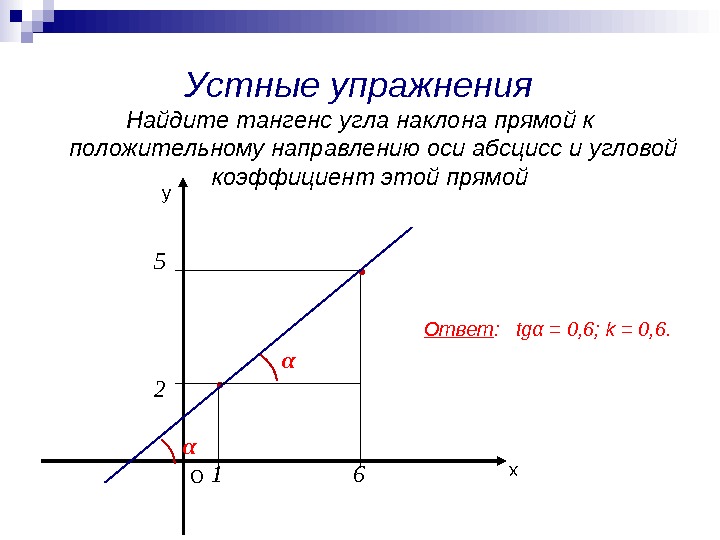
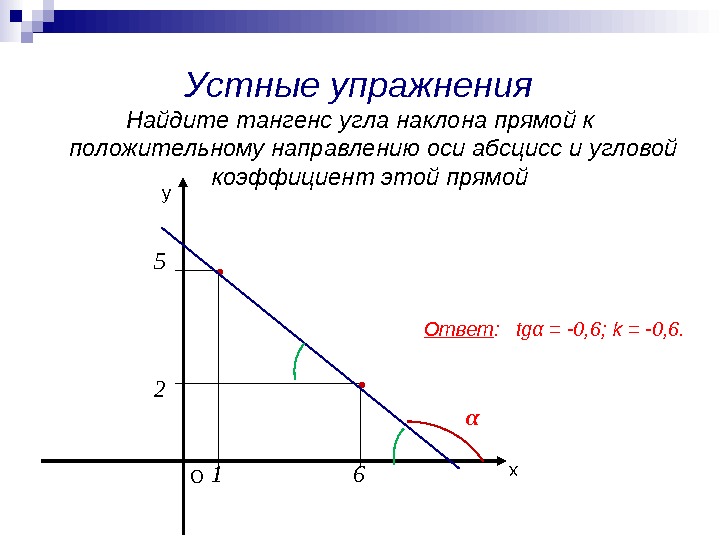
Устные упражнения Найдите тангенс угла наклона прямой к положительному направлению оси абсцисс и угловой коэффициент этой прямой ху О 12 65 αОтвет : tgα = -0, 6; k = -0, 6.

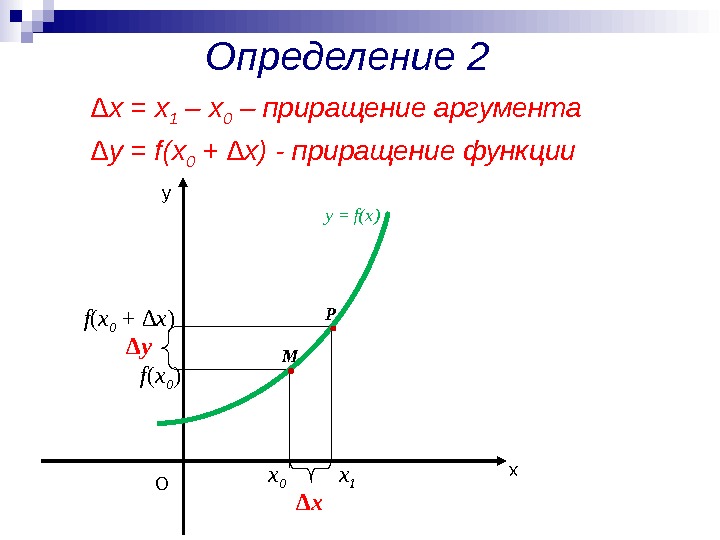
Определение 2 ∆ х = х 1 – х 0 – приращение аргумента ху у = f(x) M P О х 0 f ( х 0 ) ∆ x х 1 f ( х 0 + ∆x ) ∆ y = f(x 0 + ∆х) — приращение функции

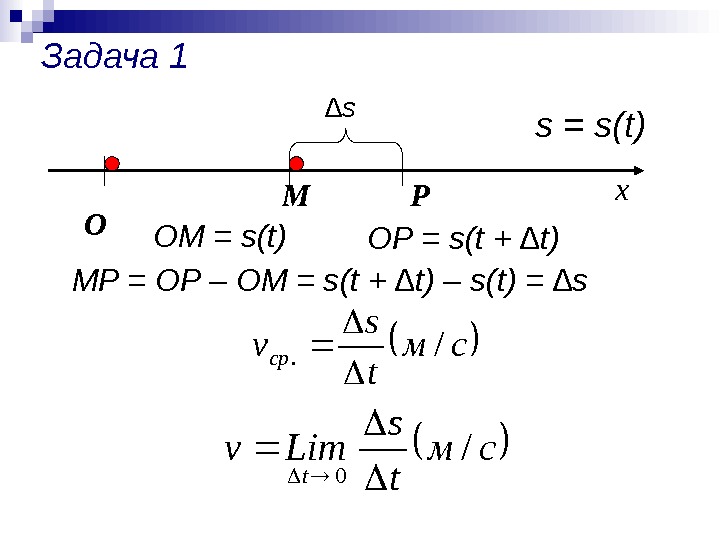
Задача 1 см t s vср/. О х М s = s(t) OM = s(t) OP = s(t + ∆t) P MP = OP – OM = s(t + ∆t) – s(t) = ∆s ∆ s см t s Limv t /

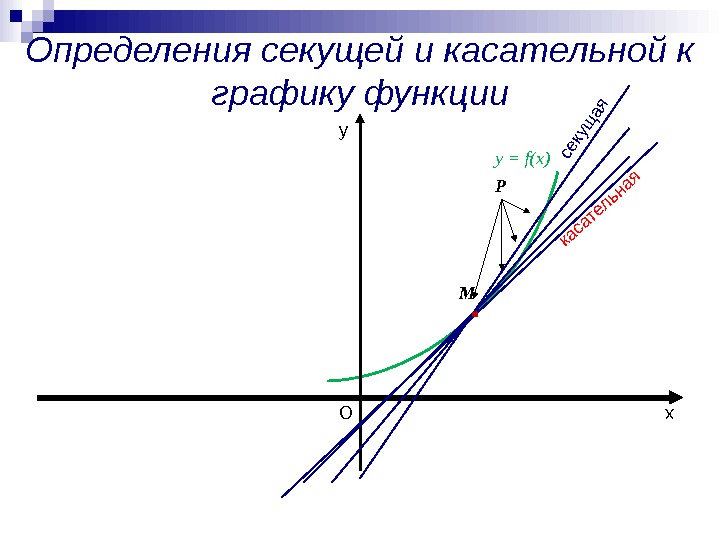
Определения секущей и касательной к графику функции ху M Pкасательная О секущ ая у = f(x)

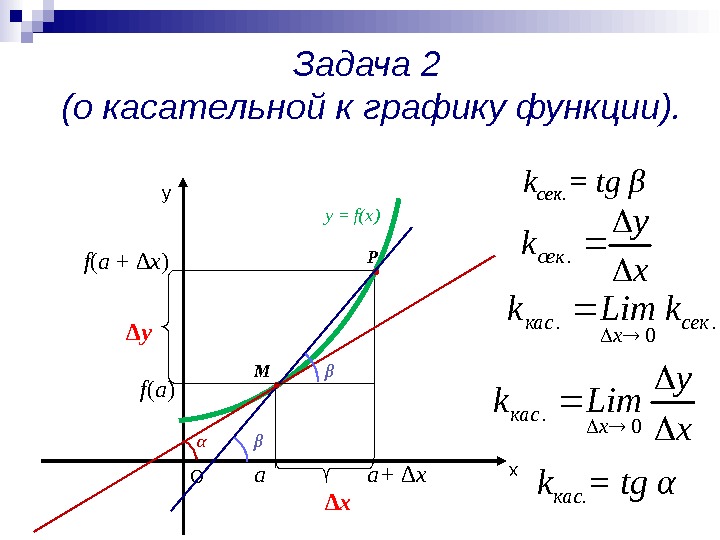
Задача 2 (о касательной к графику функции). ху у = f(x) M P О af ( a ) ∆ x a+ ∆xf ( a + ∆x ) ∆ y k сек. = tg βх у kсек . . 0. сек х кас k. Limk k кас. = tg α х у Limk х кас 0. βα β

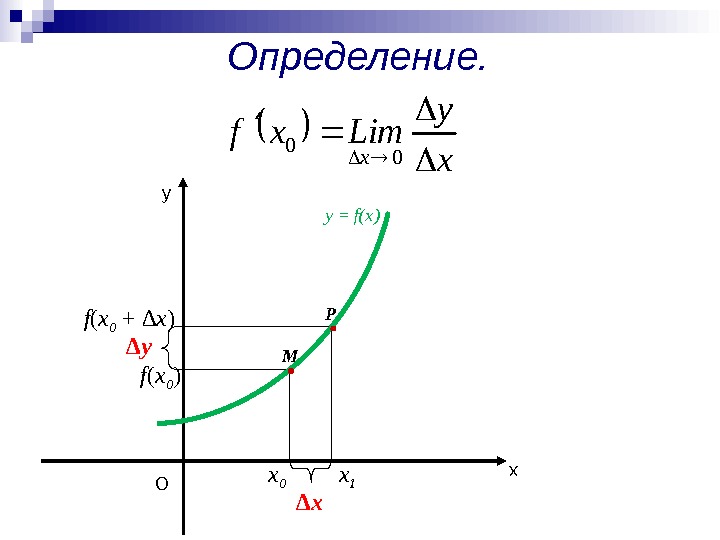
Определение. ху у = f(x) M P О х 0 f ( х 0 ) ∆ x х 1 f ( х 0 + ∆x ) ∆ y х у Limxf х

Физический смысл производной О х М s = s(t))()(tstv

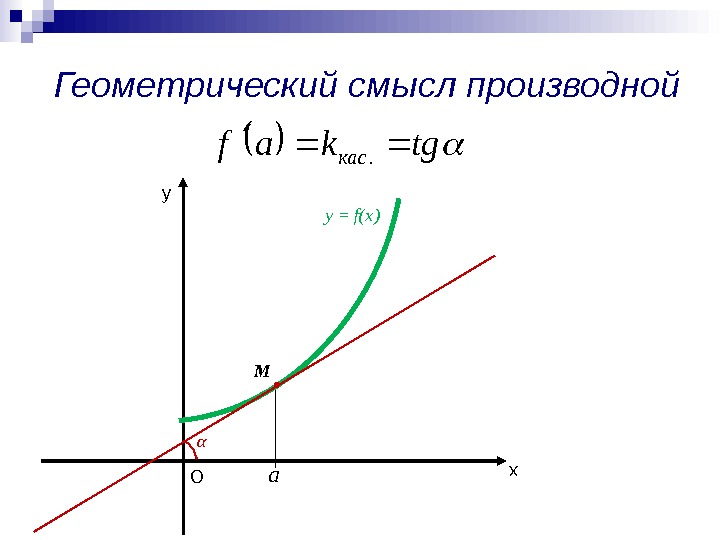
Геометрический смысл производной ху у = f(x) M О аtgkafкас. α

Алгоритм нахождения производной функции у = f(x) 1. Зафиксировать значение х, найти f(x). 2. Дать аргументу приращение Δх, перейти в новую точку х + Δх, найти f(x + Δх). 3. Найти приращение функции Δу = f(x + Δх) — f(x). 4. Составить отношение 5. Вычислить . х у . 0 х у Lim х Этот предел и есть f’(x).

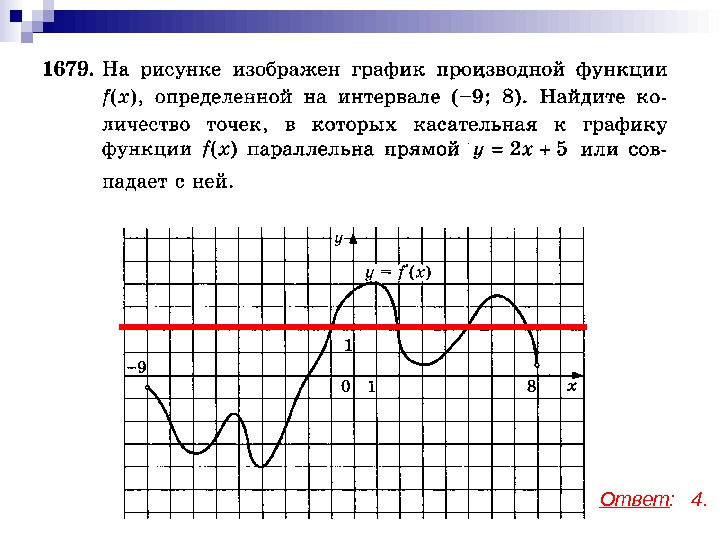
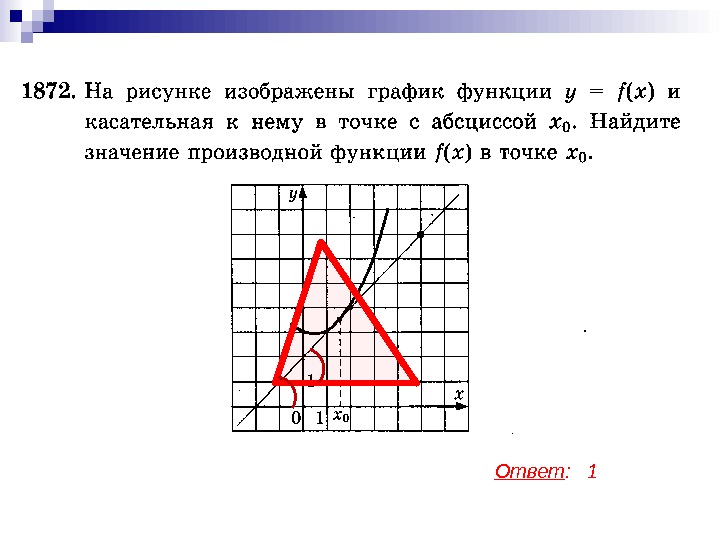
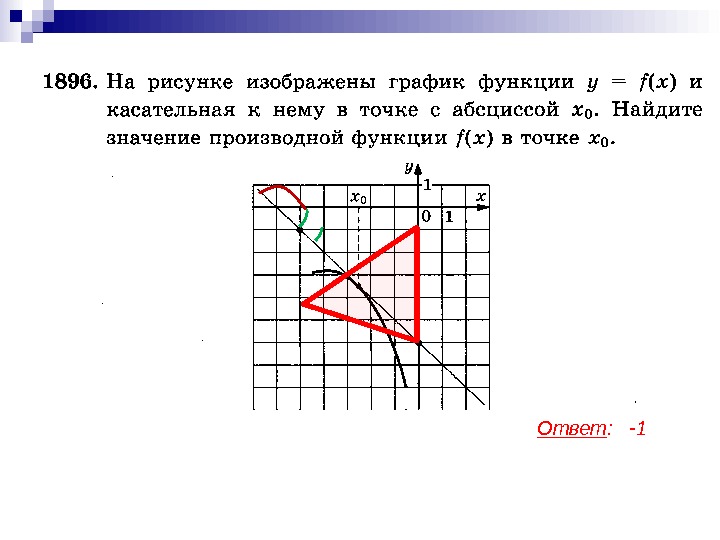
Примеры применения геометрического смысла производной.

Ответ : 4.

Ответ :

Ответ : —

Формулы дифференцирования 0 С 1 х kmkх хх2)( 2 2 11 хх

Таблица производных функций

Правила вычисления производных

Решение задач Найти производную функции Пример № 1 Общая формула производной степенной функции: Производная от x равна 1, следовательно 7*1 и получаем просто

Пример № 2 Найти производную функции Общая формула производной степенной функции: Общая формула дифференцирования произведения:

Пример № 3 Найти производную функции Общая формула производной степенной функции: Общая формула дифференцирования частного:

Пример № 4 Найти производную функции Cos (5 x – 3) Находим для начала производную от функции cos x , она будет равна – sin x. Так как у нас под знаком cos стоит функция следовательно мы должны найти производную от функции f ( 5 x – 3). Она будет равна 5 по формуле дифференцирования линейной функции. F’(5 x – 3) = 5 ( формула f’(kx – b) = k ) Следовательно f’(cos (5 x – 3) = — 5 sin (5 x – 3)

Пример № 5 Найти производную функции Для начала перепишем корень в виде степени с рациональным показателем: f(x) = (x 2 + 8 x − 7)0, 5 Теперь делаем замену: пусть x 2 + 8 x − 7 = t. Находим производную по формуле: f ’(x) = f ’(t) · t ’ = (t 0, 5 )’ · t ’ = 0, 5 · t− 0, 5 · t ’ Делаем обратную замену: t = x 2 + 8 x − 7. Имеем: f ’(x) = 0, 5 · (x 2 + 8 x − 7)− 0, 5 · (x 2 + 8 x − 7)’ = 0, 5 · (2 x + 8) · (x 2 + 8 x − 7)− 0, 5 Наконец, возвращаемся к корням: