Уравнения с одной переменной.pptx
- Количество слайдов: 43
 Уравнения с одной переменной Автор Календарева Н. Е. © 2011 г.
Уравнения с одной переменной Автор Календарева Н. Е. © 2011 г.
 План 1. Определение уравнения с одной переменной и примеры 2. Область определения уравнения 3. Корень уравнения 4. Что значит «решить уравнение» ? 5. Следствие уравнения 6. Равносильные уравнения 7. Преобразования уравнений 8. Теоремы о равносильных уравнениях
План 1. Определение уравнения с одной переменной и примеры 2. Область определения уравнения 3. Корень уравнения 4. Что значит «решить уравнение» ? 5. Следствие уравнения 6. Равносильные уравнения 7. Преобразования уравнений 8. Теоремы о равносильных уравнениях
 Знак равенства используется при записи преобразования чисел, например, sin(π/2) = 1, или 52 = 25. Это числовые равенства. Также он используется при записи тождеств: (a + b)2 = a 2 + 2 ab + b 2; sin 2 x + cos 2 x = 1. Или при записи функций f(x) = tgx ∙ cos 2 x.
Знак равенства используется при записи преобразования чисел, например, sin(π/2) = 1, или 52 = 25. Это числовые равенства. Также он используется при записи тождеств: (a + b)2 = a 2 + 2 ab + b 2; sin 2 x + cos 2 x = 1. Или при записи функций f(x) = tgx ∙ cos 2 x.
 Определение высказывания Если же будет написано, например, |x – 3| = x 2 – 1, то такая запись есть неопределенное высказывание: это высказывание может быть истинным или ложным. Под высказыванием понимают всякое утверждение, о котором имеет смысл говорить, что оно истинно или ложно.
Определение высказывания Если же будет написано, например, |x – 3| = x 2 – 1, то такая запись есть неопределенное высказывание: это высказывание может быть истинным или ложным. Под высказыванием понимают всякое утверждение, о котором имеет смысл говорить, что оно истинно или ложно.
 Примеры высказываний Столица России – город Москва. Число 221 – простое (т. е. делится само на себя или на 1). Слон – это насекомое. Любой абитуриент вуза – это студент после зачисления. x>0.
Примеры высказываний Столица России – город Москва. Число 221 – простое (т. е. делится само на себя или на 1). Слон – это насекомое. Любой абитуриент вуза – это студент после зачисления. x>0.
 Не являются высказываниями предложения, содержащие определения (например, окружностью называется геометрическое место точек плоскости, равноудаленных от заданной точки). Не являются высказываниями призывы ( «Учитесь хорошо» ) и вопросы ( «Был звонок? » )
Не являются высказываниями предложения, содержащие определения (например, окружностью называется геометрическое место точек плоскости, равноудаленных от заданной точки). Не являются высказываниями призывы ( «Учитесь хорошо» ) и вопросы ( «Был звонок? » )
 Предложения, зависящие от переменных В математике встречаются различные утверждения (предложения), зависящие от переменных, от одной переменных или нескольких. Например, натуральное число n – простое число. Это предложение зависит от переменной n. При одних значениях n оно истинно, при других – ложно.
Предложения, зависящие от переменных В математике встречаются различные утверждения (предложения), зависящие от переменных, от одной переменных или нескольких. Например, натуральное число n – простое число. Это предложение зависит от переменной n. При одних значениях n оно истинно, при других – ложно.
 Уравнения и неравенства также являются такого рода предложениями. Например, уравнение х + у = 1 является предложением, зависящим от двух переменных х и у. При х = у = 0, 5 оно истинно, при х = 2 и у = 0 оно ложно.
Уравнения и неравенства также являются такого рода предложениями. Например, уравнение х + у = 1 является предложением, зависящим от двух переменных х и у. При х = у = 0, 5 оно истинно, при х = 2 и у = 0 оно ложно.
 Если в уравнение х + у = 1 подставить конкретные числа, то данное предложение превращается в высказывание. Предложение, зависящее от переменных, при конкретных значениях переменных превращается в истинное или ложное утверждение, т. е. в высказывание.
Если в уравнение х + у = 1 подставить конкретные числа, то данное предложение превращается в высказывание. Предложение, зависящее от переменных, при конкретных значениях переменных превращается в истинное или ложное утверждение, т. е. в высказывание.
 Сложная функция Пусть на множ. X задана функция u = g(x). Обозначим U множество ее значений, т. е. E(g) = U, а область определения Def(g) = X. И пусть на множестве U определена функция y = f(u), где Def(f) = U. Тогда говорят, что на множестве X задана сложная функция у = f(g(x)), где x X. Примеры. y = sin 2 x; y = cos(x/2 − π/4); ; y = (sin| x |)2.
Сложная функция Пусть на множ. X задана функция u = g(x). Обозначим U множество ее значений, т. е. E(g) = U, а область определения Def(g) = X. И пусть на множестве U определена функция y = f(u), где Def(f) = U. Тогда говорят, что на множестве X задана сложная функция у = f(g(x)), где x X. Примеры. y = sin 2 x; y = cos(x/2 − π/4); ; y = (sin| x |)2.
 Определение уравнения с одной переменной Пусть f(x) и g(x) –функции, изучаемые в средней школе, или же это сложные функции. Рассмотрим запись f(x) = g(x). Запись вида f(x) = g(x) называется уравнением с одной переменной, если ставится задача о нахождении таких чисел х, которые обращают данное уравнение в верное числовое тождество.
Определение уравнения с одной переменной Пусть f(x) и g(x) –функции, изучаемые в средней школе, или же это сложные функции. Рассмотрим запись f(x) = g(x). Запись вида f(x) = g(x) называется уравнением с одной переменной, если ставится задача о нахождении таких чисел х, которые обращают данное уравнение в верное числовое тождество.
 Пусть дано уравнение f(x) = g(x), где f(x), g(x) – некоторые функции. Функция f(x) называется левой частью, а g(x) – правой частью уравнения. Уравнение всегда содержит знак равенства, но только один. Только один!
Пусть дано уравнение f(x) = g(x), где f(x), g(x) – некоторые функции. Функция f(x) называется левой частью, а g(x) – правой частью уравнения. Уравнение всегда содержит знак равенства, но только один. Только один!
 Примеры уравнений 1. tg 2 x + sin 4 x = 0; 2. ; 3. x 2 – 3 x + 1 = 0; 4. | x | = x. 5. sin 2 x + cos 2 x = 1 – не уравнение.
Примеры уравнений 1. tg 2 x + sin 4 x = 0; 2. ; 3. x 2 – 3 x + 1 = 0; 4. | x | = x. 5. sin 2 x + cos 2 x = 1 – не уравнение.
 Область определения уравнения Областью определения уравнения или областью допустимых значений (ОДЗ) неизвестного называется пересечение областей определения всех функций, входящих в правую и левую части уравнения.
Область определения уравнения Областью определения уравнения или областью допустимых значений (ОДЗ) неизвестного называется пересечение областей определения всех функций, входящих в правую и левую части уравнения.
 Примеры Например, в уравнении tgx + ctgx = 0 есть дроби, знаменатели которых не должны равняться 0: sinx ≠ 0 и cosx ≠ 0, т. е. x ≠ πk/2, k є Z.
Примеры Например, в уравнении tgx + ctgx = 0 есть дроби, знаменатели которых не должны равняться 0: sinx ≠ 0 и cosx ≠ 0, т. е. x ≠ πk/2, k є Z.
 Когда пишем ОДЗ? 1. В уравнении есть дробь: Знаменатель не равен нулю 2. В уравнении есть корень четной степени Подкоренное выражение 0
Когда пишем ОДЗ? 1. В уравнении есть дробь: Знаменатель не равен нулю 2. В уравнении есть корень четной степени Подкоренное выражение 0
 3. В уравнении есть тангенс или котангенс. 4. В уравнении есть логарифмическая или показательная функция. 5. Уравнение содержит все выше перечисленное в любой комбинации.
3. В уравнении есть тангенс или котангенс. 4. В уравнении есть логарифмическая или показательная функция. 5. Уравнение содержит все выше перечисленное в любой комбинации.
 Корень уравнения Число а называется корнем уравнения f(x) = g(x) , если 1) оно принадлежит области определения уравнения; 2) значения функций f(x) и g(x) в точке х = а совпадают: f(a) = g(a).
Корень уравнения Число а называется корнем уравнения f(x) = g(x) , если 1) оно принадлежит области определения уравнения; 2) значения функций f(x) и g(x) в точке х = а совпадают: f(a) = g(a).
 Таким образом, если речь идет об уравнении, то нас интересует задача нахождения корней этого уравнения. Что значит решить уравнение? Рассмотрим уравнение cos 2 x = 5/2. Оно не имеет решения. А следующее уравнение? х2 = – 1.
Таким образом, если речь идет об уравнении, то нас интересует задача нахождения корней этого уравнения. Что значит решить уравнение? Рассмотрим уравнение cos 2 x = 5/2. Оно не имеет решения. А следующее уравнение? х2 = – 1.
 Что значит «Решить уравнение» Решить уравнение – это значит, найти все его корни, или доказать, что уравнение не имеет корней. При решении уравнения применяются последовательные преобразования, которые пишем строчка под строчкой! Преобразования могут привести к потере корней или к появлению «посторонних» корней.
Что значит «Решить уравнение» Решить уравнение – это значит, найти все его корни, или доказать, что уравнение не имеет корней. При решении уравнения применяются последовательные преобразования, которые пишем строчка под строчкой! Преобразования могут привести к потере корней или к появлению «посторонних» корней.
 Потеря корней Корни теряются, когда студент сокращает левую и правую части на одинаковый множитель, стоящий в левой и правой частях и зависящий от х. Уравнение нельзя сокращать на множитель, зависящий от х.
Потеря корней Корни теряются, когда студент сокращает левую и правую части на одинаковый множитель, стоящий в левой и правой частях и зависящий от х. Уравнение нельзя сокращать на множитель, зависящий от х.
 Пример tgx = sin 2 x ОДЗ: cosx 0, т. е. х . эта серия удовлетворяет ОДЗ.
Пример tgx = sin 2 x ОДЗ: cosx 0, т. е. х . эта серия удовлетворяет ОДЗ.
 1 – sinx∙cosx = 0; sinx∙cosx = 1; | ∙ 2 2 sinx∙cosx = 2; sin 2 x = 2; x . Ответ: , где . Если бы мы сократили на одинаковый множитель sinx, наше уравнение не имело бы корней вовсе.
1 – sinx∙cosx = 0; sinx∙cosx = 1; | ∙ 2 2 sinx∙cosx = 2; sin 2 x = 2; x . Ответ: , где . Если бы мы сократили на одинаковый множитель sinx, наше уравнение не имело бы корней вовсе.
 Посторонние корни Посторонние «корни» появляются, когда возводят в квадрат левую и правую часть уравнения, или умножают обе части уравнения на множитель, зависящий от х.
Посторонние корни Посторонние «корни» появляются, когда возводят в квадрат левую и правую часть уравнения, или умножают обе части уравнения на множитель, зависящий от х.
 Пример Решим уравнение. ОДЗ: x >= 0. Решение. Так как слева неотрицательное выражение, а справа отрицательное, то решений нет. Если же возвести в квадрат, то получим х = 1. Это посторонний «корень» .
Пример Решим уравнение. ОДЗ: x >= 0. Решение. Так как слева неотрицательное выражение, а справа отрицательное, то решений нет. Если же возвести в квадрат, то получим х = 1. Это посторонний «корень» .
 Какие же преобразования допустимы? Вообще, преобразований много, ниже рассмотрим некоторые из них. По мере изучения теоретического материала будем изучать и другие преобразования, или методы решений уравнений и неравенств.
Какие же преобразования допустимы? Вообще, преобразований много, ниже рассмотрим некоторые из них. По мере изучения теоретического материала будем изучать и другие преобразования, или методы решений уравнений и неравенств.
 Равносильные уравнения Два уравнения f(x) = g(x) и f 1(x) = g 1(x) называются равносильными на некотором множестве М, если они имеют в этом множестве одни и те же решения, т. е. каждый корень первого уравнения является корнем второго, и наоборот, каждый корень второго уравнения является корнем первого, или же оба не имеют решений.
Равносильные уравнения Два уравнения f(x) = g(x) и f 1(x) = g 1(x) называются равносильными на некотором множестве М, если они имеют в этом множестве одни и те же решения, т. е. каждый корень первого уравнения является корнем второго, и наоборот, каждый корень второго уравнения является корнем первого, или же оба не имеют решений.
 Обозначения и примеры f(x) = g(x) и f 1(x) = g 1(x) равносильны: {f(x) = g(x)} <−> {f 1(x) = g 1(x)} или {f(x) = g(x)} <==> {f 1(x) = g 1(x)} Примеры. Какие уравнения равносильны? 1) х + 1 = 2 х, 2) х – 1 = 0, 3) х + 1 = 0, Ответ: 1 -е и 2 -е.
Обозначения и примеры f(x) = g(x) и f 1(x) = g 1(x) равносильны: {f(x) = g(x)} <−> {f 1(x) = g 1(x)} или {f(x) = g(x)} <==> {f 1(x) = g 1(x)} Примеры. Какие уравнения равносильны? 1) х + 1 = 2 х, 2) х – 1 = 0, 3) х + 1 = 0, Ответ: 1 -е и 2 -е.
 Какие уравнения равносильны? 3) х + 1 = 0, 5) (х + 1)3= 0, 7) х(х2 + 1) = 0, 4) х = 0, 6) х2 = х, 8) Ответы: 3 и 5; 4 и 7. .
Какие уравнения равносильны? 3) х + 1 = 0, 5) (х + 1)3= 0, 7) х(х2 + 1) = 0, 4) х = 0, 6) х2 = х, 8) Ответы: 3 и 5; 4 и 7. .
 Следствие уравнения Пусть дано уравнение f(x) = g(x). (1) Уравнение f 1(x) = g 1(x) (2) называется следствием уравнения (1), если при переходе от уравнения (1) к уравнению (2) не происходит потери корней, т. е. все корни уравнения (1) являются корнями уравнения (2).
Следствие уравнения Пусть дано уравнение f(x) = g(x). (1) Уравнение f 1(x) = g 1(x) (2) называется следствием уравнения (1), если при переходе от уравнения (1) к уравнению (2) не происходит потери корней, т. е. все корни уравнения (1) являются корнями уравнения (2).
 Преобразования уравнений Следствие обозначается стрелкой ->. Например, х =1 -> x 2 = 1. 1. Перенос слагаемого из одной части уравнения в другую: f(x) = g(x) + h(x) <==> f(x) – h(x) = g(x) В частности, f(x) = g(x) <==> f(x) – g(x) = 0 Это равносильные преобразования.
Преобразования уравнений Следствие обозначается стрелкой ->. Например, х =1 -> x 2 = 1. 1. Перенос слагаемого из одной части уравнения в другую: f(x) = g(x) + h(x) <==> f(x) – h(x) = g(x) В частности, f(x) = g(x) <==> f(x) – g(x) = 0 Это равносильные преобразования.
 Преобразования уравнений 2. Приведение подобных членов: f(x) + h(x) – h(x) = g(x) -> f(x) = g(x) Это следствие. Могут появиться посторонние корни. Рассмотрим два примера.
Преобразования уравнений 2. Приведение подобных членов: f(x) + h(x) – h(x) = g(x) -> f(x) = g(x) Это следствие. Могут появиться посторонние корни. Рассмотрим два примера.
 Пример 1 Если не написать ОДЗ и привести подобные члены, то получим следствие: х2 = 4. Или х1 = 2; х2 = 2. Появился посторонний «корень» 2. Если написать ОДЗ, то на ОДЗ уравнения равносильны.
Пример 1 Если не написать ОДЗ и привести подобные члены, то получим следствие: х2 = 4. Или х1 = 2; х2 = 2. Появился посторонний «корень» 2. Если написать ОДЗ, то на ОДЗ уравнения равносильны.
 Пример 2 Решение. Дробь равна 0 когда числитель равен 0. sin 2 x = 0; 2 x = ; . Нарисуем на круге и отберем те числа, которые удовлетворяют ОДЗ.
Пример 2 Решение. Дробь равна 0 когда числитель равен 0. sin 2 x = 0; 2 x = ; . Нарисуем на круге и отберем те числа, которые удовлетворяют ОДЗ.
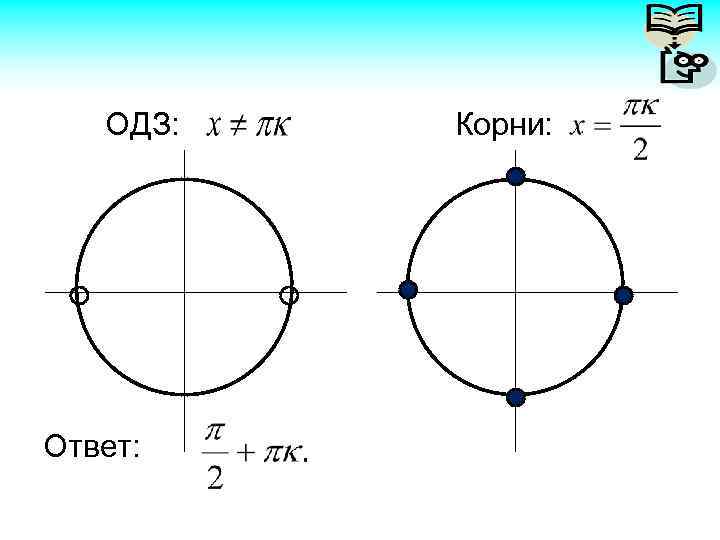 ОДЗ: Ответ: Корни:
ОДЗ: Ответ: Корни:
 Преобразования уравнений 3. Умножение обеих частей уравнения на одно и то же выражение, отличное от нуля: f(x) = g(x) <==> f(x) ∙ h(x) = g(x) ∙h(x) , где h(x) ≠ 0 на ОДЗ исходного уравнения. Это равносильные преобразования.
Преобразования уравнений 3. Умножение обеих частей уравнения на одно и то же выражение, отличное от нуля: f(x) = g(x) <==> f(x) ∙ h(x) = g(x) ∙h(x) , где h(x) ≠ 0 на ОДЗ исходного уравнения. Это равносильные преобразования.
 Пример tgx = 2 cosx ОДЗ: cosx 0, x Решение. Умножим обе части уравнения на cosx. По ОДЗ cosx 0, это равносильное преобразование. sinx = 2 cos 2 x; sinx – 2 (1 – sin 2 x) = 0; Замена sinx = t, где |t| 1.
Пример tgx = 2 cosx ОДЗ: cosx 0, x Решение. Умножим обе части уравнения на cosx. По ОДЗ cosx 0, это равносильное преобразование. sinx = 2 cos 2 x; sinx – 2 (1 – sin 2 x) = 0; Замена sinx = t, где |t| 1.
 2 t 2 + t – 2 = 0; D= 1 + 4∙ 2∙ 2 = 17; 2 t 2 + t – 2 = 0; | t | 1. Удовлетворяет системе второй корень. Ответ:
2 t 2 + t – 2 = 0; D= 1 + 4∙ 2∙ 2 = 17; 2 t 2 + t – 2 = 0; | t | 1. Удовлетворяет системе второй корень. Ответ:
 Преобразования уравнений 4. Если f(x) ∙ g(x) = 0, то f(x) = 0 или g(x) = 0, другими словами, каждое решение уравнения f(x) ∙ g(x) = 0 является решением по крайней мере одного из уравнений f(x) = 0 или g(x) = 0. Аналогично для случая, когда множителей 3, 4 и более.
Преобразования уравнений 4. Если f(x) ∙ g(x) = 0, то f(x) = 0 или g(x) = 0, другими словами, каждое решение уравнения f(x) ∙ g(x) = 0 является решением по крайней мере одного из уравнений f(x) = 0 или g(x) = 0. Аналогично для случая, когда множителей 3, 4 и более.
 Преобразования уравнений 5. Возведение обеих частей уравнения в n-ю степень, т. е. переход от уравнения f(x) = g(x) к уравнению fn(x) = gn(x), где n – произвольное натуральное число. а) Если n – нечетное число, то преобразование равносильное. б) Если n – четное число, то преобразование неравносильное.
Преобразования уравнений 5. Возведение обеих частей уравнения в n-ю степень, т. е. переход от уравнения f(x) = g(x) к уравнению fn(x) = gn(x), где n – произвольное натуральное число. а) Если n – нечетное число, то преобразование равносильное. б) Если n – четное число, то преобразование неравносильное.
 При четном n уравнение fn(x) = gn(x) равносильно уравнению | f(x) |= |g(x) |. Примером является простейшее иррациональное уравнение.
При четном n уравнение fn(x) = gn(x) равносильно уравнению | f(x) |= |g(x) |. Примером является простейшее иррациональное уравнение.
 Домашнее задание 1. 2. 3. 4. Выучить определение корня уравнения. Знать, что значит «решить уравнение» . Уметь находить ОДЗ в уравнениях Понимать, что такое равносильность уравнения.
Домашнее задание 1. 2. 3. 4. Выучить определение корня уравнения. Знать, что значит «решить уравнение» . Уметь находить ОДЗ в уравнениях Понимать, что такое равносильность уравнения.

