Учебный модуль № 1 «МЕХАНИКА МАТЕРИАЛЬНОЙ ТОЧКИ»























1.ppt
- Размер: 711.0 Кб
- Автор:
- Количество слайдов: 25
Описание презентации Учебный модуль № 1 «МЕХАНИКА МАТЕРИАЛЬНОЙ ТОЧКИ» по слайдам
 Учебный модуль № 1 «МЕХАНИКА МАТЕРИАЛЬНОЙ ТОЧКИ» Кинематика материальной точки • системы координат • кинематические характеристики • средняя и мгновенная скорости • среднее и мгновенное ускорения • движение по окружности Динамика поступательного движения • законы Ньютона • силы в природе • центр масс системы • работа и энергия • поле сил • взаимодействие материальных точек • неинерциальные системы отсчета Элементы специальной теории относительности • Принцип относительности Галилея и постулаты Эйнштейна • Преобразования Лоренца и следствия из них • Основные соотношения релятивистской механики
Учебный модуль № 1 «МЕХАНИКА МАТЕРИАЛЬНОЙ ТОЧКИ» Кинематика материальной точки • системы координат • кинематические характеристики • средняя и мгновенная скорости • среднее и мгновенное ускорения • движение по окружности Динамика поступательного движения • законы Ньютона • силы в природе • центр масс системы • работа и энергия • поле сил • взаимодействие материальных точек • неинерциальные системы отсчета Элементы специальной теории относительности • Принцип относительности Галилея и постулаты Эйнштейна • Преобразования Лоренца и следствия из них • Основные соотношения релятивистской механики
 Учебный модуль № 2 МЕХАНИКА МАТЕРИАЛЬНЫХ ТЕЛ. МОДЕЛЬ СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК • Статика • Динамика вращательного движения твердого тела • Механика жидкости
Учебный модуль № 2 МЕХАНИКА МАТЕРИАЛЬНЫХ ТЕЛ. МОДЕЛЬ СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК • Статика • Динамика вращательного движения твердого тела • Механика жидкости
 Учебный модуль № 3 МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ. ОСНОВЫ ТЕРМОДИНАМИКИ • Законы состояния идеального газа • Явления переноса • Термодинамика. Агрегатное состояние вещества
Учебный модуль № 3 МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ. ОСНОВЫ ТЕРМОДИНАМИКИ • Законы состояния идеального газа • Явления переноса • Термодинамика. Агрегатное состояние вещества
 ЛИТЕРАТУРА ОСНОВНАЯ 1. ФИЗИКА. Учебно-методический комплекс для студ. техн. спец. Часть 1. / под ред. Груздева В. А. – Новополоцк, 2009. ( или 2005 г) 2. Макаренко Г. М. Курс общей физики. — Мн. , 2003 (или 1997 г в 3 частях, тогда часть 1) 3. Физика. Методические указания и контрольные задания для студентов-заочников инженерно-технических специальностей высших учебных заведений в 3 частях. Часть 1. Физические основы механики, молекулярной физики и термодинамики / под ред. Груздева В. А. // – Новополоцк, 2006. 4. Краткий справочник по общей физике / Макаренко Г. М. , Антонович Д. А. , Вабищевич Н. В. / Новополоцк 2012 (2011, 2010) 5. Общая физика. Практикум. Часть 1 /Макаренко Г. М. , Антонович Д. А. // Новополоцк 2012. 6. Решение задач по курсу физики. Часть 1, Часть 2. /Макаренко Г. М. , Антонович Д. А. // Новополоцк 2010. 7. Макаренко Г. М. Физические основы механики. Молекулярная физика и термодинамика: сб. заданий / Г. М. Макаренко. В 3 ч. Ч. 1 – Новополцк: ПГУ 2008. – 304 с
ЛИТЕРАТУРА ОСНОВНАЯ 1. ФИЗИКА. Учебно-методический комплекс для студ. техн. спец. Часть 1. / под ред. Груздева В. А. – Новополоцк, 2009. ( или 2005 г) 2. Макаренко Г. М. Курс общей физики. — Мн. , 2003 (или 1997 г в 3 частях, тогда часть 1) 3. Физика. Методические указания и контрольные задания для студентов-заочников инженерно-технических специальностей высших учебных заведений в 3 частях. Часть 1. Физические основы механики, молекулярной физики и термодинамики / под ред. Груздева В. А. // – Новополоцк, 2006. 4. Краткий справочник по общей физике / Макаренко Г. М. , Антонович Д. А. , Вабищевич Н. В. / Новополоцк 2012 (2011, 2010) 5. Общая физика. Практикум. Часть 1 /Макаренко Г. М. , Антонович Д. А. // Новополоцк 2012. 6. Решение задач по курсу физики. Часть 1, Часть 2. /Макаренко Г. М. , Антонович Д. А. // Новополоцк 2010. 7. Макаренко Г. М. Физические основы механики. Молекулярная физика и термодинамика: сб. заданий / Г. М. Макаренко. В 3 ч. Ч. 1 – Новополцк: ПГУ 2008. – 304 с
 ЛИТЕРАТУРА ДОПОЛНИТЕЛЬНАЯ 8. Савельев, И. В. Курс общей физики / И. В. Савельев. Т. 1 -5. – М. : Астрель АСТ, 2003 -2004. 9. Детлаф А. А. , Яворский Б. М. Курс физики. — М. , 1989. Волькенштейн, В. С. 10. Фирганг, Е. В. Руководство к решению задач по курсу общей физики / Е. В. Фирганг. – СПб. : Изд-во «Лань» , 2007. – 368 с. 11. Сборник задач по общему курсу физики / В. С. Волькенштейн //С-Пб. : Книжный мир, 2007. – 365 с. 12. Трофимова Т. И. Сборник задач по курсу физики для втузов. – М. , 2003.
ЛИТЕРАТУРА ДОПОЛНИТЕЛЬНАЯ 8. Савельев, И. В. Курс общей физики / И. В. Савельев. Т. 1 -5. – М. : Астрель АСТ, 2003 -2004. 9. Детлаф А. А. , Яворский Б. М. Курс физики. — М. , 1989. Волькенштейн, В. С. 10. Фирганг, Е. В. Руководство к решению задач по курсу общей физики / Е. В. Фирганг. – СПб. : Изд-во «Лань» , 2007. – 368 с. 11. Сборник задач по общему курсу физики / В. С. Волькенштейн //С-Пб. : Книжный мир, 2007. – 365 с. 12. Трофимова Т. И. Сборник задач по курсу физики для втузов. – М. , 2003.
 Механика и ее структура Классическая механика • Кинематика • Динамика • Статика • Материальная точка • Абсолютно твердое тело • Абсолютно упругое тело • Абсолютно неупругое тело • классическая механика • релятивистская механика • квантовая механика Физические модели: линейные масштабы и промежутки времени остаются неизменными при переходе от одной системы отсчета к другой, они не зависят от выбора системы отсчета время абсолютно пространство абсолютно Постулаты классической механики
Механика и ее структура Классическая механика • Кинематика • Динамика • Статика • Материальная точка • Абсолютно твердое тело • Абсолютно упругое тело • Абсолютно неупругое тело • классическая механика • релятивистская механика • квантовая механика Физические модели: линейные масштабы и промежутки времени остаются неизменными при переходе от одной системы отсчета к другой, они не зависят от выбора системы отсчета время абсолютно пространство абсолютно Постулаты классической механики
 Механическое движение Поступательное и вращательное движение: Поступательное движение Вращение вокруг неподвижной оси. Плоское движение. Вращение вокруг неподвижной точки Свободное движение Тело отсчета. Система отсчета.
Механическое движение Поступательное и вращательное движение: Поступательное движение Вращение вокруг неподвижной оси. Плоское движение. Вращение вокруг неподвижной точки Свободное движение Тело отсчета. Система отсчета.
 СИСТЕМА КООРДИНАТcos sinr r i j r rr cos sinx r y r 2 2 2 r x y z r ( , , )M x y z
СИСТЕМА КООРДИНАТcos sinr r i j r rr cos sinx r y r 2 2 2 r x y z r ( , , )M x y z
 СИСТЕМА КООРДИНАТ 2 2 arccos x x y 2 2 arccos 2 x y z r x y
СИСТЕМА КООРДИНАТ 2 2 arccos x x y 2 2 arccos 2 x y z r x y
 СКОРОСТЬ Мгновенная скорость Средняя скорость неравномерного движения (другое название — средняя путевая скорость). Длина пути s, пройденного точкой за промежуток времени от t 1 до t 2 Если модуль скорости увеличивается с течением времени, то движение называется ускоренным, если же он убывает с течением времени, то движение называется замедленным. Вектор средней скорости
СКОРОСТЬ Мгновенная скорость Средняя скорость неравномерного движения (другое название — средняя путевая скорость). Длина пути s, пройденного точкой за промежуток времени от t 1 до t 2 Если модуль скорости увеличивается с течением времени, то движение называется ускоренным, если же он убывает с течением времени, то движение называется замедленным. Вектор средней скорости
 УСКОРЕНИЕ Мгновенное ускорение Среднее ускорение В общем случае плоского криволинейного движения вектор ускорения удобно представить в виде суммы двух проекций
УСКОРЕНИЕ Мгновенное ускорение Среднее ускорение В общем случае плоского криволинейного движения вектор ускорения удобно представить в виде суммы двух проекций
 Тангенциальное ускорение Нормальное ускорение Полное ускорение
Тангенциальное ускорение Нормальное ускорение Полное ускорение
 Виды движения • прямолинейное равномерное • прямолинейное равнопеременное (равноускоренное) • равномерное движение по окружности • криволинейное равнопеременное
Виды движения • прямолинейное равномерное • прямолинейное равнопеременное (равноускоренное) • равномерное движение по окружности • криволинейное равнопеременное
 Закон движения( ) ( ) x x t y y t z z t 2 1( ) t t. S t t dt
Закон движения( ) ( ) x x t y y t z z t 2 1( ) t t. S t t dt
 ( ) ( )r x t i y t j z t k rr rr. Векторный способ описания движения
( ) ( )r x t i y t j z t k rr rr. Векторный способ описания движения
 yxz x y z drdrdr dr i j k dt dt r r rr ( ) ( )x x x y y y z z z drdx t dt dt drdy t dt dt dr dz t dt dt 2 2 2 x y z r cos x cos z cos y Скорость
yxz x y z drdrdr dr i j k dt dt r r rr ( ) ( )x x x y y y z z z drdx t dt dt drdy t dt dt dr dz t dt dt 2 2 2 x y z r cos x cos z cos y Скорость
 yxz x y z ddd d a i j k a i a j a k dt dt r r rr ( ) ( ) x x x y y y z z z d a a t dt 2 2 2 x y za a a r / cos xa a / cos za a / cos ya a Ускорение
yxz x y z ddd d a i j k a i a j a k dt dt r r rr ( ) ( ) x x x y y y z z z d a a t dt 2 2 2 x y za a a r / cos xa a / cos za a / cos ya a Ускорение
 Естественно-параметрический способ описания движения Дуговой координатой I называется измеренное вдоль траектории расстояние от точки О (начала отсчета) до частицы Вектор — это единичный вектор, связанный с частицей и направленный по касательной к траектории в сторону возрастания дуговой координаты. Скорость частицы
Естественно-параметрический способ описания движения Дуговой координатой I называется измеренное вдоль траектории расстояние от точки О (начала отсчета) до частицы Вектор — это единичный вектор, связанный с частицей и направленный по касательной к траектории в сторону возрастания дуговой координаты. Скорость частицы
 Естественно-параметрический способ описания движения Ускорение частицы
Естественно-параметрический способ описания движения Ускорение частицы
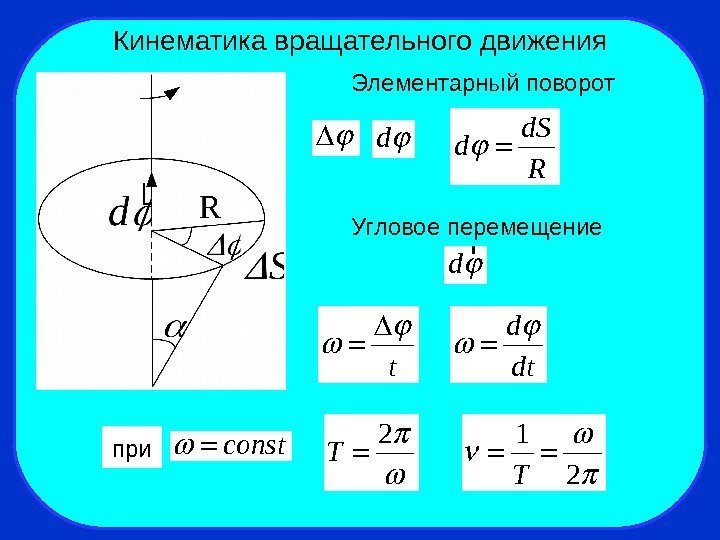
 Кинематика вращательного движенияd Элементарный поворот d. S d R d r Угловое перемещение 2 T 1 2 T t d dt при const
Кинематика вращательного движенияd Элементарный поворот d. S d R d r Угловое перемещение 2 T 1 2 T t d dt при const
 Кинематика вращательного движения 2 d dt r r 0 t 2 0 0 2 t t 0 t 2 2 2 1 2 ; t
Кинематика вращательного движения 2 d dt r r 0 t 2 0 0 2 t t 0 t 2 2 2 1 2 ; t
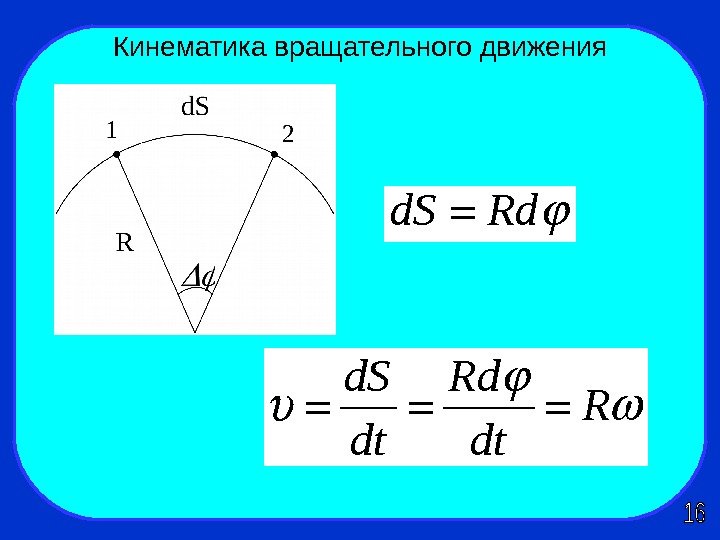
 Кинематика вращательного движенияd. S Rd R dt dt
Кинематика вращательного движенияd. S Rd R dt dt
 Кинематика вращательного движения 2 2 n R a R R ( )d d R d a R R dt dt dt 2 2 4 2 na a a R d S dt R dt
Кинематика вращательного движения 2 2 n R a R R ( )d d R d a R R dt dt dt 2 2 4 2 na a a R d S dt R dt
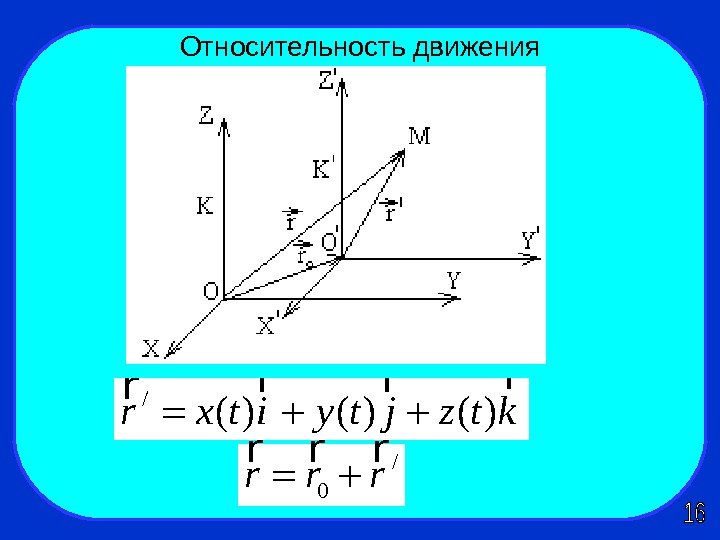
 Относительность движения/ ( ) ( )r x t i y t j z t k rr rr / 0 r r r
Относительность движения/ ( ) ( )r x t i y t j z t k rr rr / 0 r r r
 Относительность движения/ отн dr dx dy dz i j k dt dt r rr rr 2 2 2 отн d x d y d z a i j k dt dt dt rr rr 0 0 абс отн drdr dx dy dz i j k dt dt dt rr rr rr r r 0 абс отнa a a r r r 1 2. . . a a a r r r
Относительность движения/ отн dr dx dy dz i j k dt dt r rr rr 2 2 2 отн d x d y d z a i j k dt dt dt rr rr 0 0 абс отн drdr dx dy dz i j k dt dt dt rr rr rr r r 0 абс отнa a a r r r 1 2. . . a a a r r r

