TWO-PORT NETWORKS In many situations one is not

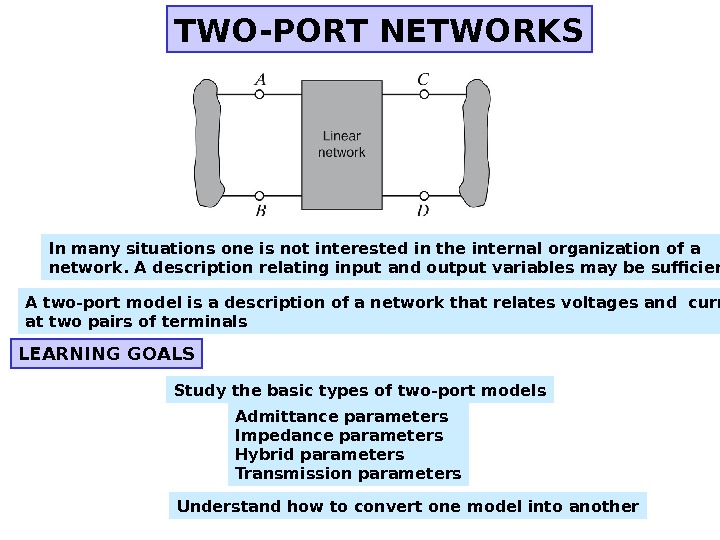
TWO-PORT NETWORKS In many situations one is not interested in the internal organization of a network. A description relating input and output variables may be sufficient A two-port model is a description of a network that relates voltages and currents at two pairs of terminals Admittance parameters Impedance parameters Hybrid parameters Transmission parameters. LEARNING GOALS Study the basic types of two-port models Understand how to convert one model into another

ADMITTANCE PARAMETERS The admittance parameters describe the currents in terms of the voltages 2221212 2121111 Vy. Vy. I The first subindex identifies the output port. The second the input port. 1 port to applied is voltage a and circuited-short is port the when 2 port into flowing current the determines 21 y The computation of the parameters follows directly from the definition 021 12 011 11 12 VV V I y 022 22 012 21 12 VV V I y. The network contains NO independent sources

LEARNING EXAMPLE Find the admittance parameters for the network 2221212 2121111 Vy. Vy. I ][ 2 3 ) 2 1 1( 1111 Sy. VI 2111, yy determine to used Circuit 2 I 1212 2 1 21 1 VIII][ 2 1 21 Sy 2212, yy determine to used Circuit ][ 65 31 21 2222 Sy. VI ][ 21 65 53 32 3 12221 Sy. VII Next we show one use of this model

An application of the admittance parameters 2221212 2121111 Vy. Vy. I 212 211 65 21 21 23 VVI 2214, 2 IVAI The model plus the conditions at the ports are sufficient to determine the other variables. 21 21 41 65 21 0 21 23 2 VV VV 22 4 1 VI ][ 11 2 ][ 11 8613 2 2 21 AI VV VV Determine the current through the 4 Ohm resistor

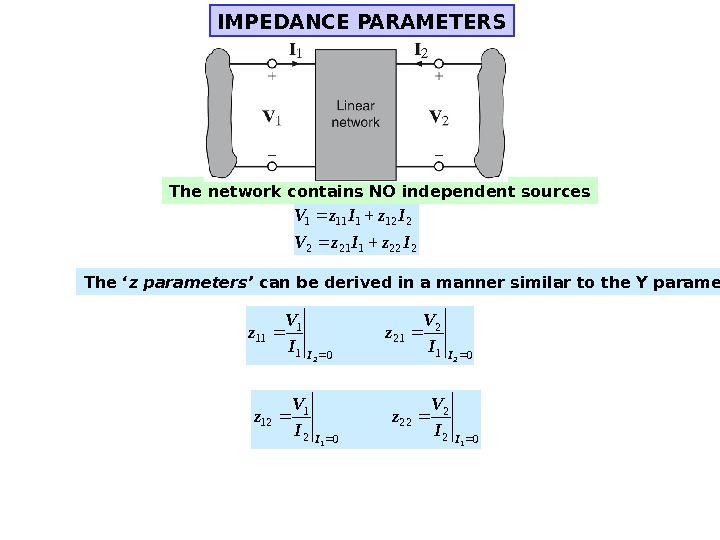
IMPEDANCE PARAMETERS The network contains NO independent sources 2221212 2121111 Iz. Iz. V The ‘ z parameters’ can be derived in a manner similar to the Y parameters 01 2 21 01 1 11 22 III V z 02 2 22 02 1 12 11 III V z

LEARNING EXAMPLE Find the Z parameters Write the loop equations )(42 1222 2111 IIj. V IIj. IV 24 442 2221 1211 jzjz 212 211 24 4)42( Ij. Ij. V rearranging 01 2 21 01 1 11 22 III V z 02 2 22 02 1 12 11 III V z 2221212 2121111 Iz. Iz. V

LEARNING EXAMPLE Use the Z parameters to find the current through the 4 Ohm resistor 2221212 2121111 Iz. Iz. V Output port constraint 224 IV Input port constraint 11)1(012 IV 212 211 24 4)42( Ij. Ij. V 21)24(40 Ij. Ij 214)43(12 Ij. Ij )43(j 4 j 2))43)(24(16(48 Ijjj 73. 13761. 12 I

HYBRID PARAMETERS The network contains NO independent sources 2221212 2121111 Vh. Ih. V admittance output circuit-open gain current forward circuit-short gain voltage reverse circuit-open impedance input circuit-short 22 21 12 11 h h These parameters are very common in modeling transistors 01 2 21 01 1 11 22 VVI I h I V h 02 2 22 02 1 12 11 IIV I h V V h

LEARNING EXAMPLE Find the hybrid parameters for the network 1 I 1 V 2 I 2 V 2221212 2121111 Vh. Ih. V 1 I 1 V 2 I 02 V 14))3||6(12(1111 h. IV 32 63 6 2112 h. II 1 V 2 I 2 V 01 I 32 63 6 1221 h. VV ][ 91 9 222 2 Sh. V I

TRANSMISSION PARAMETERS The network contains NO independent sources 221 DICVI BIAVV 021 22 II V I C V V A 021 02 1 22 VV I I D I V B ratio current circuit-short negative D admittance transfer circuit-open C impedance transfer circuit-short negative B ratio voltage circuit open. A ABCD parameters

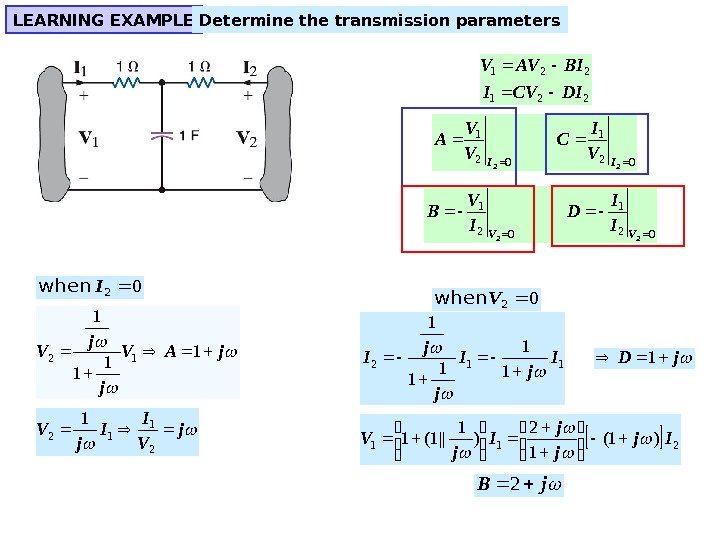
LEARNING EXAMPLE Determine the transmission parameters 221 DICVI BIAVV 021 22 II V I C V V A 021 02 1 22 VV I I D I V B j. AV jj V 1 1 12 j V I I j. V 21 12 1 02 I when 02 V when 112 1 1 1 I jj I j. D 1 211 )1( 1 2 )1 ||1(1 Ij j j I j. V j.

PARAMETER CONVERSIONS If all parameters exist, they can be related by conventional algebraic manipulations. As an example consider the relationship between Z and Y parameters 211 2221 1211 21 2221212 2121111 V V zz zz I I zz zz V V Iz. Iz. V 21 2221 1211 V V yy yy 1 2221 1211 zz zz yy yy 1121 12221 zz zz Z 12212211 zzzz. Z with In the following conversion table, the symbol stands for the determinant of the corresponding matrix DC BA hh hh yy yy zz zz THYZ , , ,

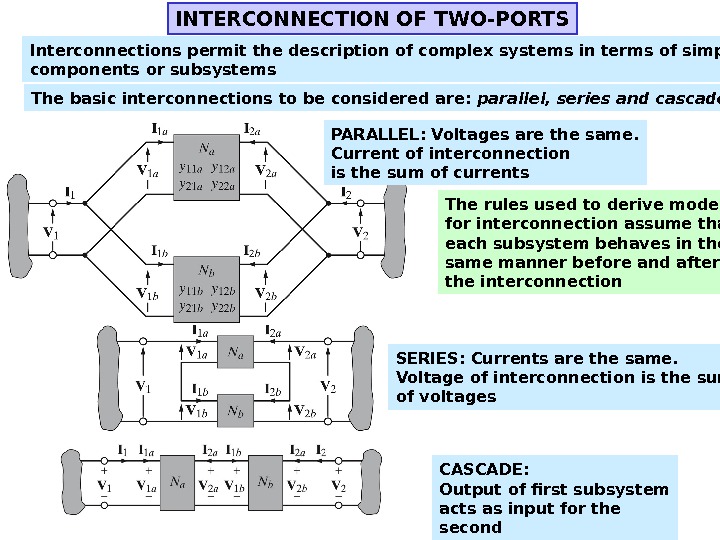
INTERCONNECTION OF TWO-PORTS Interconnections permit the description of complex systems in terms of simpler components or subsystems The basic interconnections to be considered are: parallel, series and cascade PARALLEL: Voltages are the same. Current of interconnection is the sum of currents The rules used to derive models for interconnection assume that each subsystem behaves in the same manner before and after the interconnection SERIES: Currents are the same. Voltage of interconnection is the sum of voltages CASCADE: Output of first subsystem acts as input for the second

aaa ba aa a. VYI yy yy Y V V V I I I 2221 1211 21 21, , bbb. VYI manner similar a In baba VVVVVV IIIIII 222111 , , : sconstraint ction. Interconne ba ba VVV III ba. YYY VYYVYVYIbabbaa)(Parallel Interconnection: Description Using Y Parameters YVI V V yy yy I I 2 1 2221 1211 2 1 ndescriptio ction. Interconne

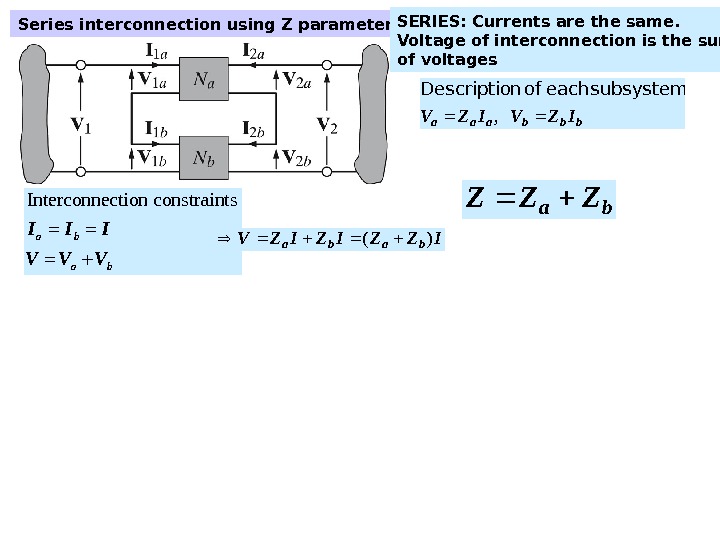
Series interconnection using Z parameters bbbaaa IZVIZV , subsystem each of n. Descriptio Interconnection constraints a b. I I I V V V IZZIZIZVbaba)( ba. ZZZ SERIES: Currents are the same. Voltage of interconnection is the sum of voltages

Cascade connection using transmission parameters 2 1 1 1 2 2 Interconnection constraints: a b a b. I I V V V I I a a aa aa a a I V DC BA I V 2 2 1 1 b b bb bb b b I V DC BA I V 2 2 1 1 2 2 1 1 I V DC BA I V bb bb aa aa Matrix multiplication does not commute. Order of the interconnection is important CASCADE: Output of first subsystem acts as input for the second 2 2 1 1 I V DC BA I V 221 DICVI BIAVV

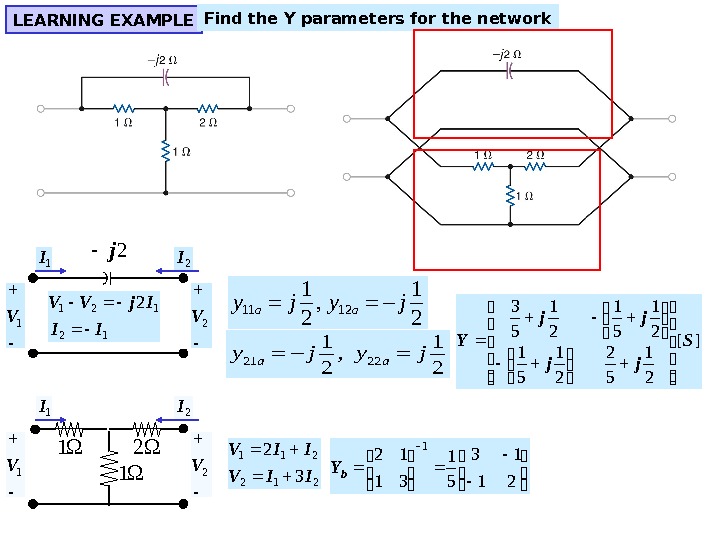
LEARNING EXAMPLE Find the Y parameters for the network 1 1 2 2 j 1 I 1 V 2 I 2 V 12 121 2 II Ij. VV 11 12 1 1 , 2 2 a ay j 21 22 1 1 , 2 2 a ay j 212 211 32 IIV 21 13 51 31 12 1 b. Y ][ 21 5 2 21 51 21 5 3 S jj jj Y

LEARNING EXAMPLE Find the Z parameters of the network Network A Network BUse direct method, or given the Y parameters transform to Z … or decompose the network in a series connection of simpler networks j jj j Z a 23 42 23 22 11 11 b. Z j j j j ZZZ ba

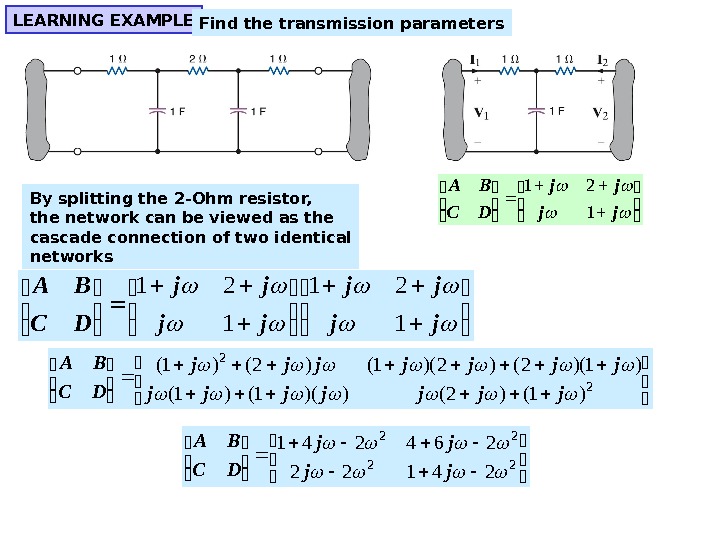
LEARNING EXAMPLE Find the transmission parameters By splitting the 2 -Ohm resistor, the network can be viewed as the cascade connection of two identical networks jj jj DC BA 1 21 2 2 )1()2())(1()1( )1)(2()2)(1()2()1( jjjjjjj DC BA 22 22 24122 264241 jj jj