Точка х 0 называется точкой максимума функции

Точка х 0 называется точкой максимума функции f(x ), если в некоторой окрестности точки х 0 выполняется неравенство )()(0 xfxf

Точка х 1 называется точкой минимума функции f(x ), если в некоторой окрестности точки х 1 выполняется неравенство )()( 1 xfxf Значения функции в точках х 0 и х 1 называются соответственно максимумом и минимумом функции. Максимум и минимум функции называется экстремумом функции.

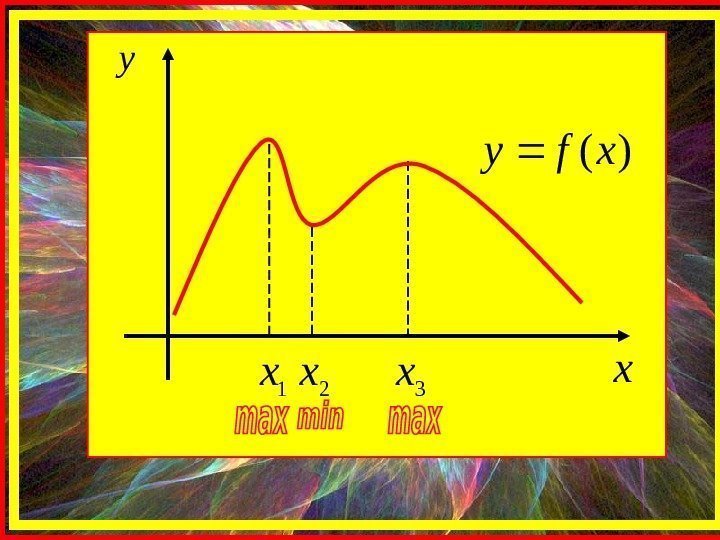
x y )(xfy 1 x 2 x 3 x

На одном промежутке функция может иметь несколько экстремумов, причем может быть, что минимум в одной точке больше максимума в другой. Максимум или минимум функции на некотором промежутке не являются в общем случае наибольшим и наименьшим значением функции. Если в некоторой точке хх 00 дифференцируемая функция f(xf(x )) имеет экстремум, то в некоторой окрестности этой точки выполняется теорема Ферма и производная функции в этой точке равна нулю: 0)( 0 xf

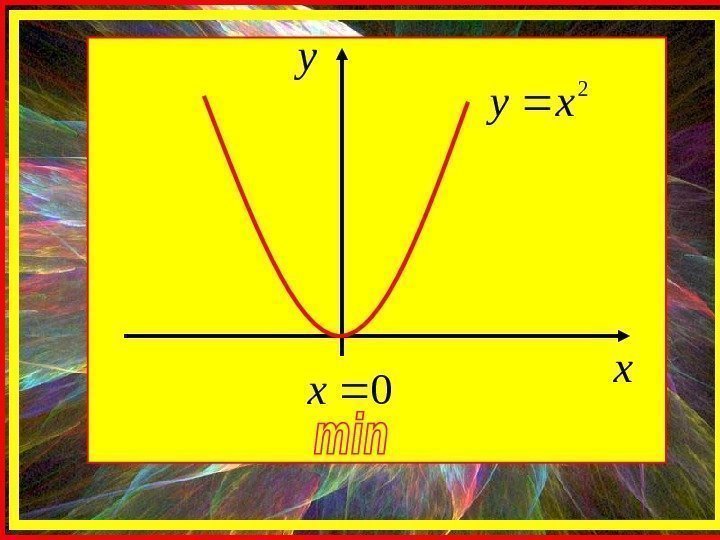
Однако, функция может иметь экстремум в точке, в которой она не дифференцируема. Например, функцияxy имеет минимум в точке 0 x но она в этой точке не дифференцируема.

Для того, чтобы функция y=f(x) имела экстремум в точке х 0 , необходимо, чтобы ее производная в этой точке равнялась нулю или не существовала.

Точки, в которых выполняется необходимое условие экстремума, называются критическими или стационарными. Т. об. , если в какой-либо точке имеется экстремум, то эта точка является критической. Но критическая точка не обязательно является точкой экстремума.

Найти критические точки и экстремумы функций: 1 2 xy

Применим необходимое условие экстремума: xxy 2)( 2 002 xприxy 0 0 y x — критическая точка

x y 2 xy 0 x

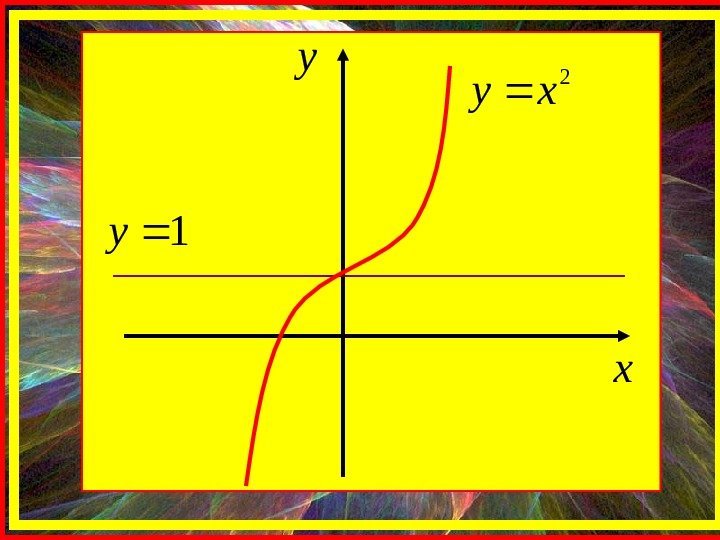
2 13 xy

Применим необходимое условие экстремума: 23 3)1(xxy 003 2 xприxy 1 0 y x — критическая точка

x y 2 xy 1 y

Если при переходе через точку х 0 производная дифференцируемой функции y=f(x) меняет знак с плюса на минус, то х 0 есть точка максимума, а если с минуса на плюс, то х 0 есть точка минимума.

Пусть производная меняет знак с плюса на минус, т. е. на некотором интервале 0 ; xa 0)(xf а на некотором интервале bx; 0 0)(xf Тогда функция y=f(x) будет возрастать на 0 ; xa

и будет убывать на bx; 0 По определению возрастающей функции 00 ; )()(xaxвсехдляxfxf Для убывающей функции bxxвсехдляxfxf; )()( 00 0 x -точка максимума. Аналогично доказывается для минимума.

1 Найти производную функции)(xfy 2 Найти критические точки функции, в которых производная равна нулю или не существует.

3 Исследовать знак производной слева и справа от каждой критической точки. 4 Найти экстремум функции.

Исследовать функцию на экстремум: 3 )1(xxy

Применим схему исследования функции на экстремум: 1 Находим производную функции: 233 )1(3)1())1((xxxxxy )14()1()31()1( 22 xxxxx

2 Находим критические точки: 0)14()1( 2 xx 4 1 1 2 1 x x

3 Исследуем знак производной слева и справа от каждой критической точки: x 4 1 1 y y В точке х=1 х=1 экстремума нет.

4 Находим экстремум функции: 256 27 4 1 min f

Если первая производная дифференцируемой функции y=f(x) в точке х 0 равна нулю, а вторая производная в этой точке положительна, то х 0 есть точка минимума, а если вторая производная отрицательна, то х 0 есть точка максимума.

Пусть 0)( 0 xf следовательно 0)( 0 xf и в некоторой окрестности точки х 00 , т. е. 0)()( xfxf

функцияba; будет возрастать на )(xf содержащем точку х 00. . Но Но 0)( 0 xf на интервале 0 ; xa 0)(xf а на интервале bx; 0 0)(xf

Таким образом, функция при переходе через точку х 00 меняет знак с минуса на плюс, следовательно эта точка является точкой минимума. )(xf Аналогично доказывается случай для максимума функции.

Схема исследования функции на экстремум в этом случае аналогична предыдущей, но третий пункт следует заменить на: 3 Найти вторую производную и определить ее знак в каждой критической точке.

Из второго достаточного условия следует, что если в критической точке вторая производная функции не равна нулю, то эта точка является точкой экстремума. Обратное утверждение не верно: если в критической точке вторая производная функции равна нулю, то эта точка также может являться точкой экстремума. В этом случае для исследования функции необходимо использовать первое достаточное условие экстремума.