ТЕПЛОПЕРЕДАЧА Теорией теплообмена (теплопередачей), называется наука изучающая процессы

ТЕПЛОПЕРЕДАЧА Теорией теплообмена (теплопередачей), называется наука изучающая процессы передачи теплоты (теплообмен между телами) и распределение температуры в твердых, жидких и газообразных телах. Различают три основные формы передачи теплоты: теплопроводность, конвективный теплообмен и лучистый теплообмен. Теплопроводностью называется процесс передачи теплоты путем непосредственного соприкосновения тел или отдельных частей тела, за счет передачи энергии движения одних микрочастиц другим.

В чистом виде теплопроводность наблюдается в твердых телах, а также в неподвижных газах и жидкостях в том случае, когда в них отсутствует конвекция. В металлах перенос теплоты осуществляется путем движения (диффузии) свободных электронов; передача теплоты за счет упругих колебаний кристаллической решетки второстепенна. В жидкостях и твердых телах – диэлектриках теплопроводность осуществляется упругими волнам. В газообразных телах распространение теплоты теплопроводностью происходит вследствие обмена энергией при соударении молекул, имеющих различную скорость теплового движения (путем диффузии молекул и атомов

Конвекция – процесс переноса теплоты при перемещении объемов жидкости или газа в пространстве из области одной температуры в область с другой температурой. Конвективным теплообменном называется процесс передачи теплоты, в котором совместно участвуют теплопроводность и конвекция. В зависимости от причины вызывающей движение жидкости, различают конвективный теплообмен при свободном движении жидкости (свободная конвекция) и конвективный теплообмен при вынужденном движении жидкости (вынужденная конвекция). Свободная конвекция возникает вследствие разности плотностей неравномерно нагретых слоев жидкости или газа в поле сил тяготения. Вынужденная конвекция возникает под влиянием внешнего воздействия (например, ветра, насоса, компрессора, вентилятора и т. д. ),

Тепловым излучением называется процесс переноса теплоты в пространстве электромагнитными волнами. Лучистым теплообменом называется процесс передачи теплоты излучением между телами, который включает последовательное превращение внутренней энергии тела в энергию излучения, распространение ее в пространстве и превращение энергии излучения во внутреннюю энергию другого тела. Основные положения теории теплопроводности Температурное поле. В общем случае процесс передачи теплоты теплопроводностью в твердом теле сопровождается изменением температуры как, в пространстве, так и во времени. Совокупность значений температуры в данный момент времени для всех точек пространства, определяемых координатами называется температурным полем

Математическим выражением температурного поля записанное в неявной форме Различают стационарное (установившееся) и нестационарное (неустановившееся) температурные поля. Стационарное температурное поле наблюдается в том случае, когда температура в различных точках пространства не изменяется во времени. Если температура изменяется во времени – температурное поле называется нестационарным. Температурное поле может быть функцией трех, двух и одной координаты. Соответственно оно называется трех-, двух и одномерным. Простейшее одномерное стационарное температурное поле, z, y, xft )x(ft

В соответствии с классификацией температурного поля принципиально различают стационарный и нестационарный процессы передачи теплоты. Аналитическое исследование теплопроводности сводится к изучению пространственно-временного изменения температуры, т. е. нахождению уравнения температурного поля в явном виде. Температурный градиент. Если соединить точки тела, имеющие одинаковую температуру, получим поверхность равных температур, называемую изотермической. Изотермической поверхностью тела называется геометрическое место точек, имеющих одинаковую температуру. Поскольку в одной и той же точке тела одновременно не может быть двух различных значений температуры, изотермические поверхности не могут пересекаться, они либо замыкаются внутри самого тела либо обрываются на границах тела.

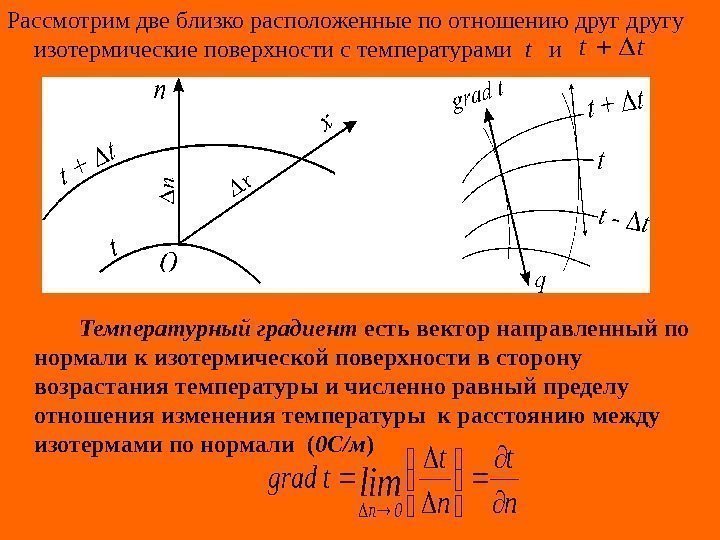
Рассмотрим две близко расположенные по отношению другу изотермические поверхности с температурами t и Температурный градиент есть вектор направленный по нормали к изотермической поверхности в сторону возрастания температуры и численно равный пределу отношения изменения температуры к расстоянию между изотермами по нормали ( 0 С/м )tt n t tgradlim 0 n

В случае трехмерного температурного поля суммарный температурный градиент определяется по правилу сложения векторов где – единичные векторы в направлении. Тепловой поток. Закон Фурье Согласно гипотезе Фурье количество теплоты проходящий через элемент изотермической поверхности за промежуток времени , пропорционально температурному градиентуzyx kgradtjgradtigradt k, j, i dd. F n t dd. Fgradt. Q

Количество теплоты, проходящее в единицу времени через единицу площади изотермической поверхности , называется плотностью теплового потока. Количества теплоты , проходящее в единицу времени через изотермическую поверхность, называется тепловым потоком ( Дж/с =Вт ) d. Fd Q q d. F n t d. Fq. Q

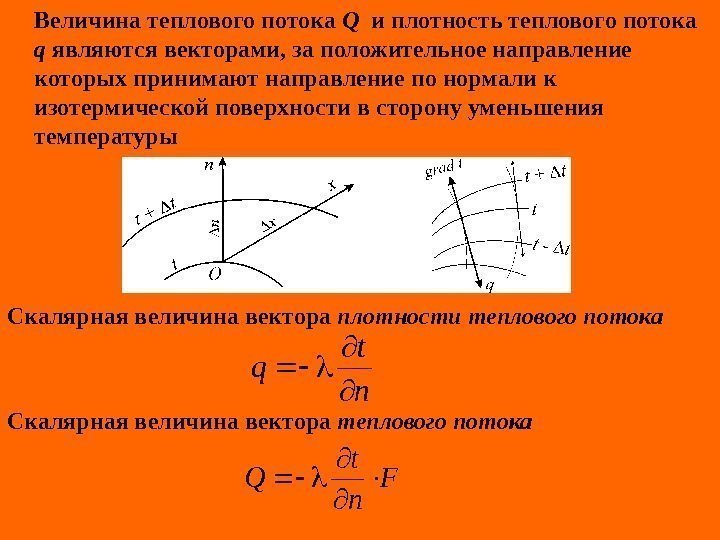
Величина теплового потока Q и плотность теплового потока q являются векторами, за положительное направление которых принимают направление по нормали к изотермической поверхности в сторону уменьшения температуры Скалярная величина вектора плотности теплового потока Скалярная величина вектора теплового потока n t q F n t Q

Полное количество теплоты, проходящее через изотермическую поверхность за время Выражение плотности тепловых потоков в направлении осей Вектор теплового потока для трехмерной задачи d. Fd n t Q 0 F ; x t qx ; y t q y z t q z zyx kqjqiqq

Коэффициент теплопроводности. Под коэффициентом теплопроводности понимают тепловой поток, передаваемый через единичную поверхность при единичном значении температурного градиента Для каждого тела коэффициент теплопроводности имеет свое численное значение и, зависит от природы, пористости, влажности, давления, температуры и других параметров. Для многих материалов с достаточной для практики степенью точности, зависимость коэффициента теплопроводности от температуры можно принять линейнойgradt. F Q , b

Наихудшими проводниками теплоты являются газы. Коэффициент теплопроводности газов возрастает с увеличением температуры и изменяется в пределах 0, 005 – 0, 5 Вт/(м·°C). Коэффициент теплопроводности жидкостей лежит в пределах 0, 07 – 0, 7 Вт/(м·°C) и, как правило (за исключением воды и глицерина), уменьшается с увеличением температуры. Наилучшими проводниками теплоты являются металлы, у которых Вт/(м·°C). У большей части металлов с возрастанием температуры он уменьшается. Вещества с коэффициентом теплопроводности меньше называются теплоизоляционными

Дифференциальное уравнение теплопроводности при следующих допущениях: тело однородно и изотропно; физические параметры тела постоянны во времени и пространстве; температурные деформации рассматриваемого элементарного объема малы по сравнению с самим объемом; внутренние источники теплоты распределены в рассматриваемом объеме равномерно; макрочастицы тела неподвижны относительно друга; имеет следующий вид: c q z t y t x t a c q ta tv 2 2 2 v

где – время, сек ; – коэффициент температуро- проводности, характеризующий скорость изменения температуры в любой точке тела, ; – теплоемкость тела; – плотность тела; – объемная плотность тепловыде-ления, в m /м 3 ; – оператор Лапласа. В цилиндрических координатах где – радиус вектор; – угол наклона радиуса–вектора c a c vq c q z tt r 1 r t a tv 2 2 22 2 r

Условия однозначности или краевые условия: геометрические условия (форма, размеры тела); физические условия (физические свойства тела и его физические параметры); начальные условия (распределение температуры в теле в начальный момент времени); граничные условия, определяющие взаимодействие тела с окружающей средой. 1. Граничные условия первого рода. Задается распределение температуры на поверхности тела, как функция координат и времени: где -температура поверхности тела. В частном случае, если температура поверхности тела постоянна, , z, y, xft c ct consttc

2. Граничные условия второго рода. Задается распределение плотности потока на поверхности тела, как функция координат и времени В частном случае, когда плотность теплового потока на поверхности тела остается постоянной, имеем . 3. Граничные условия третьего рода. Задается температура окружающей среды и закон теплообмена между поверхностью тела и окружающей средой (закон Ньютона-Рихмана ). если , где – коэффициент теплообмена, представляющий собой плотность теплового потока подведенного (отведенного) к единице поверхности тела при разности температур между поверхностью тела и окружающей среды 10 С , в m /м 2 град. , z, y, xfqc constqq 0 c жcttqжсtt

Количество теплоты, воспринятое поверхностью тела, распространяется в нем по закону Фурье Отсюда аналитическое выражение граничных условий третьего рода 4. Граничные условия четвертого рода. Отражают условия теплообмена системы тел имеющих различные коэффи-циенты теплопроводности. Между телами предполагается идеальный контакт. c жc n t tt жс c tt n t с 2 2 с 1 1 n t

Теплопроводность при стационарном режиме При установившемся (стационарном) тепловом режиме , поэтому Развернутая форма оператора зависит от выбранной системы координат. При отсутствии внутренних источников теплоты , уравнение теплопроводности при стационарном температурном поле запишется в виде 0 t 0 c q ta v 2 t 2 0 t

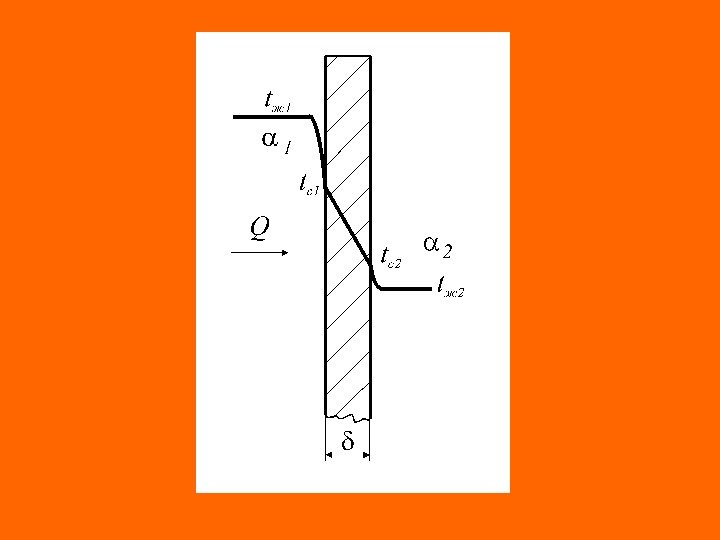
Определим тепловой поток теплопроводностью через изотропную плоскую стенку , предполагая, что температура меняется только в направлении, перпендикулярном плоскости стенки т. е; 0 z t y t 0 dx td x t

Первое и второе интегрирование данного уравнение Постоянные интегрирования определяются из граничных условий первого рода 0 dx td 2 2 ; C dx dt 121 Cx. Ct 2 c 1 c 12 c 1 c 21 c tt Cttxпри t. C; tt 0 xпри

Подставляя постоянные интегрирования в общее решение получим закон распределения температуры в рассматривае-мом сечении стенки распределение температуры в стенке при граничных условиях первого рода является линейной функцией. Расчетное выражение удельного теплового потока получается из уравнения Фурьеx tt tt 2 c 1 c 1 c 2 c 1 c 1 ttc x t q

С учетом того, что тепловой поток имеем Отношение называется тепловой проводимостью стенки. Обратная величина представляет собой термическое сопротивление стенки. С учетом выше сказанного имеем q. FQ Fttq. FQ 2 c 1 c ; tt q 2 с1 с F tt q. FQ 2 с1 с

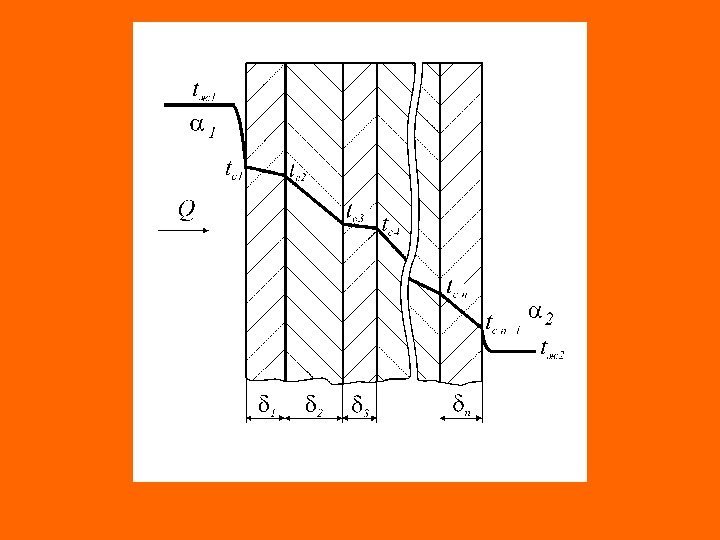
Рассмотрим передачу тепла теплопроводностью через плоскую трехслойную стенку при условиях: толщина слоев стенки ; коэффициенты теплопроводности материалов соответственно ; контакт между стенками идеальный и температура на границе смежных слоев одинакова. 321, ,

Перенос тепла происходит в стационарных условиях – плотность теплового потока по всем слоям стенки имеет одно и то же значение ( q = idem ). Выделим из этого ряда равенств разности температур . ttttttq 4 c 3 c 3 3 3 c 2 c 2 2 2 c 1 c 1 1 ; q. Rqtt 1 1 1 2 c 1 с ; q. Rqtt 2 2 2 3 c 2 c . q. Rqtt 3 3 3 4 с

Складывая левые и правые части уравнений разности температур, получаем слева изменение температуры в стенке, справа – произведение плотности теплового потока q и общего термического сопротивления Плотности теплового потока при переносе тепла теплопроводностью через плоскую трехслойную стенку . RRRqqtt 321 3 3 2 2 1 1 4 с1 с , RRR tttt q 321 4 с1 с 33 22 11 4 с1 с q. FQ

В общем случае для стенки, состоящей из n – слоев имеем Температура на стыке двух слоев , R tttt q 1 nс1 с n 1 i i 1 nс1 с n 1 ii i 1 nс1 с , F R tt F tt q. FQ n 1 i i 1 nс1 с n 1 ii i 1 nс1 с i 1 i ii 11 i qtt

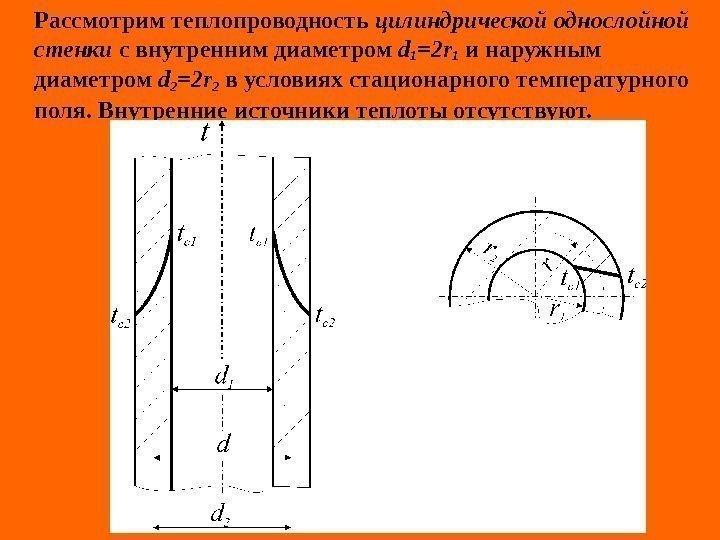
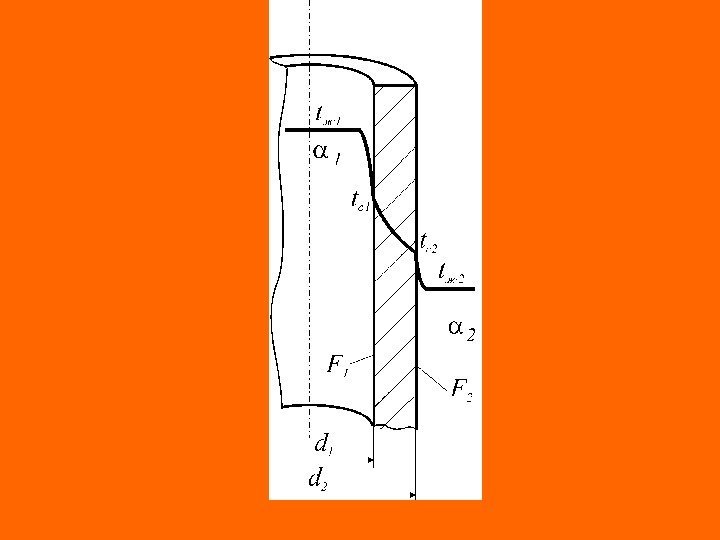
Рассмотрим теплопроводность цилиндрической однослойной стенки с внутренним диаметром d 1 =2 r 1 и наружным диаметром d 2 =2 r 2 в условиях стационарного температурного поля. Внутренние источники теплоты отсутствуют.

Уравнение теплопроводности цилиндрической стенки В рассматриваемом случае Температуры на наружной и внутренней поверхности цилиндрической стенки неизменны и ось z совмещена с осью цилиндра 2 2 22 2 z tt r 1 r t a t 0 t 0 z tt

Предположим, что в рассматриваемом случае температура изменяется только в радиальном направлении Граничные условия: введем новую переменную тогда 0 dr dt r 1 rd td 2 2 1 с1 ttrr 2 с2 ttrr dr dt u 0 r u dr du

интегрируя потенцируя и переходя к первоначальным переменным, получаем После интегрирования имеем Постоянные С 1 и С 2 определяются из граничных условий 1 Clnrlnuln r dr Cdt 1 21 Crln. Ct 2111 c Crln. Ct 2222 c. Crln. Ct

Подставляя полученные значения С 1 и С 2 в общее уравнение получим температурного поля представляет собой уравнение логарифмической кривой. 1 2 c 1 c 1 c r r ln tttt 2 1 2 c 1 c 1 r r ln tt С 2 1 1 2 c 1 c 1 c 2 r r ln rln ttt. С

Для определения теплового потока через цилиндрическую поверхность воспользуемся законом Фурье Подставляя в уравнение Фурье значение градиента температуры получим ; F r t Q r. L 2 r t Q rdr dt 1 С 1 2 2 c 1 c rr ln ttl 2 Q 12 2 c 1 c dd ln ttl 2 Qили

Тепловой поток может быть отнесен либо к единице длины, либо к единице внутренней или внешней поверхности. внутренней поверхности наружной поверхности Тепловой поток отнесенный к единице длины, имеет размерность В m /м и называется линейной плотностью теплового потока. 1 2 c 1 c 1 1 d d ln 2 1 d tt q ld Q 1 2 2 2 c 1 c 1 2 d d ln 2 1 d tt q ld Q 1 2 2 c 1 c l d d ln 2 1 tt q l Q

Рассуждая аналогично, как при получении расчетного соотношения теплового потока для многослойной плоской стенки, можно получить выражение для определения линейной плотности теплового потока в случае многослойной цилиндрической стенки называется полным термическим сопротивлением теплопроводности многослойной цилиндрической стенки. Температура на границе любых двух слоев : ni 1 i i 1 nc 1 c l d d ln 2 1 tt q ni 1 i id d ln 2 1 i i l cic di dq tt 1 1 1)1(ln

Обобщенное уравнение стационарной теплопроводности При передаче тепла через произвольные криволинейные стенки тепловой поток определяется по такому же уравнению, как и для плоской стенки, только в выражение вводится расчетная поверхность теплопроводности Расчетная поверхность теплопроводности принимается в зависимости от вида стенки, через которую происходит передача тепла: • Для плоской стенки • Для цилиндрической стенки • Для сферической стенки . tt. FQ 21 m ; 321 FFFFm ; ln 1212 FFFFFFm. Lm. 21 FFFFm. Gm

Теплопроводность через многослойные криволинейные стенки определяется по уравнению аналогичному уравнению теплопроводности плоской многослойной стенки где – толщина, коэффициент теплопроводности и расчетная поверхность рассматриваемого слоя. n 1 imii i 1 nс1 с F tt Qmiii F, ,

Основные положения конвективного теплообмена Количество теплоты, отдаваемое жидкостью твердой стенке или воспринимаемое жидкостью от стенки, определяется уравнением Ньютона–Рихмана а плотность теплового потока следующим образом где α – коэффициент, характеризующий условия теплообмена между жидкостью и поверхностью твердого тела, называемый коэффициентом теплоотдачи , Вт/(м 2·°C) . Коэффициент теплоотдачи есть плотность теплового потока ( q ) на поверхности тела, отнесенная к разности температур поверхности тела и окружающей среды. , Ftt. Q жс жсttq

Коэффициент теплоотдачи зависит в наиболее общем случае является функцией формы и размера тела, режима движения жидкости, физических свойств жидкости, положения в пространстве и состояние поверхности теплообмена и других величин. Возникновение и интенсивность свободного или естественного движения всецело определяется тепловыми условиями процесса и, зависят от рода жидкости, разности температур и объема пространства, в котором протекает процесс. Вынужденное движение в общем случае может сопровождает-ся свободным движением. Доля в переносе тепла свободной конвекцией тем больше, чем больше разница в температуре отдельных частей среды и чем меньше скорость вынужденного движения. При больших скоростях вынужденного движения, влияние свободной конвекции становится пренебрежимо малым.

Практически изучение процесса теплоотдачи сводится к определению зависимости ( ) от различных факторов. В дальнейшем будут рассмотрены только стационарные процессы течения и теплоотдачи. Условием стационарности является неизменность во времени скорости и температуры в любой точке жидкости. Дифференциальные уравнения конвективного теплообмена Дифференциальное уравнение конвективного теплообмена получается при рассмотрении передачи теплоты теплопроводностью через, практический, неподвижный слой жидкости (пограничный слой), который имеет место вблизи твердого тела, омываемого жидкостью ( ) и передачи теплоты к пограничному слою за счет конвективного теплообмена ( ) жn t q жсttq

Дифференциальное уравнение энергии при условии однородности и несжимаемости жидкости, отсутствия внутренних источников теплоты и работы расширения, а также постоянства физических параметров жидкости в пределах элементарного объема формулируется следующим образом: -характеризует локальное изменение температуры во времени в какой-либо точке жидкости; жжcn t tt , ta d Dt 2 z t w y t w x t w t d Dt zyx t

– характеризует конвективное изменение температуры при переходе от точки к точке. Дифференциальное уравнение неразрывности получается на основе закона сохранения массы и, для сжимаемой жидкости имеет следующий вид: В частном случае несжимаемых жидкостей уравнение запишется в видеz t w y t w x t wzyx 0 z w y w x wzyx 0 z w y w x w zyx

Уравнение движения (уравнение Навье-Стокса) получается на базе первого и второго законов Ньютона и в векторной форме записи можно представить в виде Полученная система дифференциальных уравнений описывает бесчисленное множество конкретных процессов. Точные решения этой системы имеются только для отдельных частных случаев при ряде упрощающих предпосылок. Основы теории подобия и метода анализа размерностей В связи с ограниченными возможностями аналитического решения дифференциальных уравнений конвективного теплообмена решающее значение приобретает эксперимент. , wpg d w.

Проведение экспериментов на моделях с целью получения зависимостей для определения коэффициента теплоотдачи предполагает наличие теории, которая давала бы ответ на следующие вопросы: 1) как смоделировать реальный процесс; 2) какие величины нужно измерять в опыте; 3) как обрабатывать данные опыта; 4) на какие явления можно в дальнейшем распространить полученные расчетные зависимости. На все эти вопросы дает ответы теория подобия. Понятие подобия заимствовано из геометрии, где рассматриваются условия подобия геометрических фигур. Для подобия геометрических фигур достаточно соблюдения обычных признаков подобия (пропорциональность сходственных сторон, равенство углов и др. ).

Для подобия физических процессов необходимо говорить о подобии физических величин и явлений. Два или несколько явлений будут подобны, если подобны все физические величины , характеризующие эти явления, т. е. подобные между собою явления имеют одинаковые критерии подобия. Важной теоремой теории подобия является утверждение о том, что решение дифференциального уравнения, описывающего данный процесс, может быть представлено в виде функциональной зависимости между критериями подобия, характеризующими этот процесс и полученными из исходного уравнения. Наряду с приведенными выше двумя теоремами подобия, важным является и утверждение о том, что подобны между собой те явления, которые принадлежат к одному классу, к одному роду и имеют равные определяющие критерии подобия.

Теория подобия используется при наличии дифференциаль-ных уравнений, описывающих рассматриваемый процесс, позволяет не решая сами уравнения, получить выражения чисел (критериев) подобия и на их основе получить расчетные зависимости – уравнения подобия. При отсутствии дифференциальных уравнений, описывающих изучаемый процесс, используется теория размерностей. Однако в этом случае должен быть известен перечень основных величин, оказывающих существенное влияние на развитие рассматриваемого процесса. Например, для свободной конвекции такой перечень величин определяется следующей исходной зависимостью: , c, , , g, lf P

Теория размерностей в этом случае позволяет свести данное выражение от семи независимых переменных к зависимости от двух обобщенных переменных (к уравнению подобия). Критерии подобия и критериальные уравнения Рассмотрим безразмерные комплексы величин, входящие в дифференциальные уравнения, представленные в безразмерной форме: Безразмерные комплексы, составленные из размерных величин, называются критериями подобия. , ltg ; a lw ; l

Число Нуссельта , или критерий теплоотдачи, характеризует соотношение тепловых потоков, передаваемых конвекцией и теплопроводностью по нормали через пристенный слой Число Рейнольдса – критерий гидродинамического подобия, характеризуется соотношением сил инерции и молекуляр-ного трения (вязкости), l. Nu l , Rel

Число Прандтля характеризует физические свойства жидкости и их влияние на конвективный теплообмен Число Пекле – критерий конвективного теплообмена, характеризует отношение плотности теплового потока, передаваемого конвекцией, к плотности теплового потока, передаваемого теплопроводностью, al. Pе p p c a a c , Pr. Re. Pe

Число Грасгофа характеризует соотношение подъемной силы, возникшей вследствие разности плотностей нагретых и холодных частиц жидкости и силы молекулярного трения, интенсивность свободного движения жидкости: Как было рассмотрено ранее, система дифференциальных уравнений, характеризующая процесс, приводится к безразмерному виду при соответствующих условиях однозначности. В конечном счете получается общий вид критериального уравнения 23 lg. Gr. Bi, Fo, Gr. Pr, Re, , , w, w, w, z, y, xf. Nu zyx

Важное значение, при решении задач нестационарной теплопроводности, имеют критерии подобия (Фурье) и (Био). Критерий Фурье ( ) — характеризует безразмерное время. Написание Критерия Био похоже на форму записи критерия Нуссельта Следует отметить, что. поскольку критериальные уравнения получены на основе эксперимента, в каждом случае указывается: диапазон применимости уравнения; определяющая температура ( при которой определяются теплофизические свойства вещества) и линейный размер. Fo Bi 2 0 l a Fo 0 l Bi

Теплообмен при свободной конвекции При изучении свободной конвекции рассматриваются три характерных случая: теплообмен между жидкостью и телом, расположенным в неограниченном пространстве; теплообмен в ограниченных прослойках. Коэффициент теплоотдачи при свободном движении жидкости в большом объеме определяется из следующих уравнений подобия: Конвективный теплообмен при свободной конвекции на вертикальной поверхности. для вертикальных труб и плоских стенок при ламинарном течении жидкости (103 <Gr ·Pr <109 ) ; Pr. Pr. Gr 76, 0 Nu 25, 0 cж 25,

для вертикальных труб и плоских стенок при турбулентном течении жидкости (Gr ·Pr ) >109 В этих уравнениях определяющей температурой является температура окружающей среды, за определяющий размер принимается длина участка от начала теплообмена l. Конвективный теплообмен при свободной конвекции у горизонтального цилиндра. При эначениях 10 -3 < < 5 102 значение коэффициента теплоотдачи определяется уравнением. Pr. Pr. Gr 15, 0 Nu 25, 0 cж 33, 0 m. Pr. Gr 18, 1 Nu 8/

при значениях комплекса 103 109 уравнение имеет вид В качестве определяющего размера принят внешний диаметр, за определяющую температуру – температура окружающей среды. Конвективный теплообмен при свободной конвекции на горизонтальной стенке. Для расчета теплообмена на горизонтальной плоской поверхности можно воспользоваться следующим уравнением: Pr. Gr 25, 0 cж 25, 0 Pr. Pr. Gr 5, 0 Nu , Pr. Grc. Nu n

при ; при За определяющий размер принимается ширина пластины, за определяющую температуру . Если тепло-отдача направлена верх, то результаты расчетов необходимо увеличить на 30%, если вниз – уменьшить на 30%. Конвективный теплообмен при свободной конвекции в ограниченном пространстве В вертикальных каналах, если расстояние между поверхностями велико, восходящее и нисходящее движение протекает без взаимных помех и имеет такой же характер, как и в неограниченном пространстве 3/1 n, 135, 0 c 10 Pr. Gr 102 137 . 4/1 n, 54, 0 c 102 Pr. Gr 7 жсmtt 5, 0 t

Если же расстояние между поверхностями мало, то вследствие взаимных помех возникают внутренние циркуляционные контуры, высота которых определяется шириной щели, видом жидкости и интенсивностью процесса. Для очень узких щелей в которых жидкость практически неподвижна теплообмен, в этом случае осуществляется чистой теплопроводностью. Для упрощения расчетов переноса теплоты в ограниченных пространствах сложный процесс конвективного теплообмена заменяют эквивалентным процессом теплопроводности. и конвекцией k

Коэффициент , определяется следующим образом при В качестве определяющего линейного размера принимается толщина прослойки; определяющей температуры – средняя температура жидкости tж. , 10 Pr. Gr 3 ; 1 k , 10 Pr. Gr 3 25, 0 k. Pr. Gr 18, 0 k 25, 0 k. Pr. Gr 18,

Конвективный теплообмен при вынужденном движении жидкости Течение жидкости в трубах может быть ламинарным, переходным и турбулентным в зависимости от числа Рейнольдса. Ламинарное движение наблюдается при При возмущения потока необратимо нарушают ламинарный режим движения и способствуют турбулизации потока. Однако турбулентное движение устанавливается при При числах Рейнольдса от до движение жидкости является переходным от ламинарного к турбулентному. Теплообмен при ламинарном движении жидкости в трубах При ламинарном течении жидкости в трубах возможны два режима движения: вязкостный и вязкостно-гравитационный. . 2200 Re. Re 1 кр 2200 Re. 10 Re. Re 4 2 кр 3 102,

Вязкостный режим существует при ( Gr. Pr ) 8· 105 , средний коэффициент теплоотдачи в этом случае определяется по формуле . l d Re 55, 1 Nu 14, 0 жc 31 2 tttлc лt. Pr. Pr. Gr. Pr. Re 15, 0 Nu 25, 0 cж 1, 033,

Теплообмен при турбулентном движении жидкости в трубах Для определения среднего коэффициента теплоотдачи при развитом турбулентном движении обычно используется формула М. А. Михеева В качестве определяющего линейного размера здесь принят внутренний диаметр трубы; определяющая температура – средняя температура потока. Теплообмен при поперечном обтекании труб жидкостью Для определения коэффициента теплоотдачи при поперечном обтекании одиночной трубы используют следующие уравнения подобия: . Pr. Pr. Re 021, 0 Nu 25, 0 cж 43, 08,

при Re = 5 ÷ 103 при Re = 10 3 ÷ 2· 105 За определяющий линейный размер принят внешний диаметр трубы; за определяющую температуру – температура набегающего потока. Теплообмен при продольном обтекании жидкостью плоской поверхности Среднее значение коэффициента теплоотдачи при обтекании плоской стенки определяется из уравнения Rе ≤ 4· 10 4 Rе > 4· 104 ; Pr. Pr. Re 5, 0 Nu 25, 0 cж 38, 05, 0 . Pr. Pr. Re 25, 0 Nu 25, 0 cж 38, 06, 0 25, 0 сж 33, 05, 0 Pr/Pr. Re 66, 0 Nu 25, 0 сж 33, 08, 0 Pr/Pr. Re 037, 0 Nu

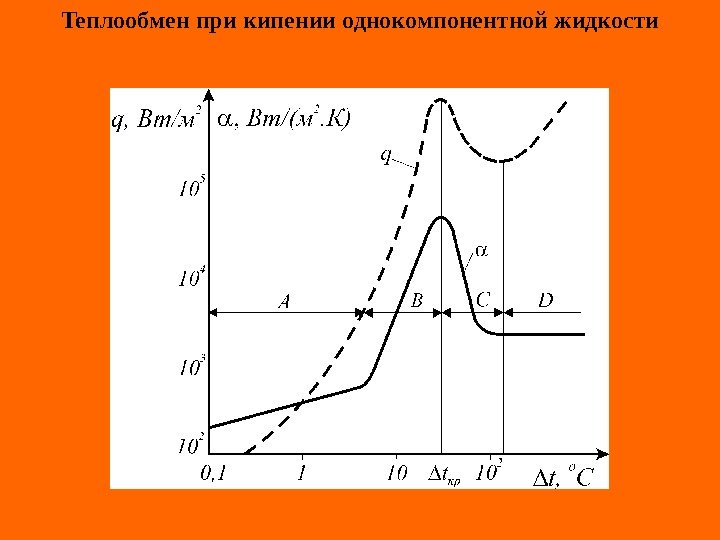
Теплообмен при кипении однокомпонентной жидкости

В практических расчетах пузырькового кипения воды удобно пользоваться следующими уравнениями: При пленочном кипении средний коэффициент теплоотдачи определяется следующим образом: на вертикальной поверхности на горизонтальном цилиндре ; pq 38, 415, 07, 0 . pt 106 5, 033, 2 4 п пп 3 п ht gr 667, 0 4 п пп 3 п dt gr 53,

Теплообмен при конденсации чистого пара При соприкосновении пара со стенкой, температура которой ниже температуры насыщения ts , пар конденсируется в зависимости от состояния поверхности стенки; образовавшаяся жидкость может принимать форму капель или пленки. В соответствии с этим конденсация пара называется капельной и пленочной. для вертикальной стенки или трубы высотой h для горизонтальной трубы диаметром d где – критерий конденсации; r – теплота конденсации, ; Pr. Ко 42, 0 Nu 25, 0 cж 25, 0 , Pr. Ко 72, 0 Nu 25, 0 cж 25, 0 trlgtcarlg. Ko 3 P

На волновой характер излучения влияют корпускулярные свойства, которые заключаются в том, что лучистая энергия излучается материальными телами не непрерывно, а отдельными дискретными порциями – квантами света, или фотонами. Все виды электромагнитного излучения имеют одинаковую природу и отличаются только длиной волны. Большая часть твердых и жидких тел имеет сплошной спектр излучения, т. е. излучает энергию во всем диапазоне длин волн. Некоторые тела (чистые металлы, газы и др. ) излучают энергию только в определенных интервалах длин волн. Такое излучение называется выборочным или селективным. Количество энергии излучаемой твердыми и жидкими те- лами увеличивается с ростом температуры тела, для них характерно излучение и поглощение лучистой энергии тонким поверхностным слоем.

Количество энергии излучаемой газами зависит от температуры, толщины слоя и давления газа. В газах излучение и поглощение энергии происходит всем объемом. Некоторые виды излучения обладают свойством превращаться в тепловую энергию при поглощении телами, вызывая нагревание. Это свойство излучения определяется длиной волны. В наибольшей мере такими свойствами обладает видимое инфракрасное (тепловое) излучение. Количество энергии, излучаемое поверхностью тела во всем интервале длин волн (о т λ=О до λ=∞) в единицу времени, называется полным (интегральным) лучистым потоком Q ( Вт ). Излучение, соответствующее узкому интервалу длин волн, называется монохроматическим.

Лучистый поток, исходящий с единицы поверхности излучающего тела по всем направлениям полупространства называется плотностью интегрального излучения E ( Вт/м 2 ) Лучистый поток , исходящий со всей поверхности излучающего тела равен Плотность интегрального излучения, отнесенная к рассматриваемому диапазону длин волн, называется спектральной интенсивностью излучения ( Вт/м 3 ) F d. FEQ d d. E E d. F d. Q

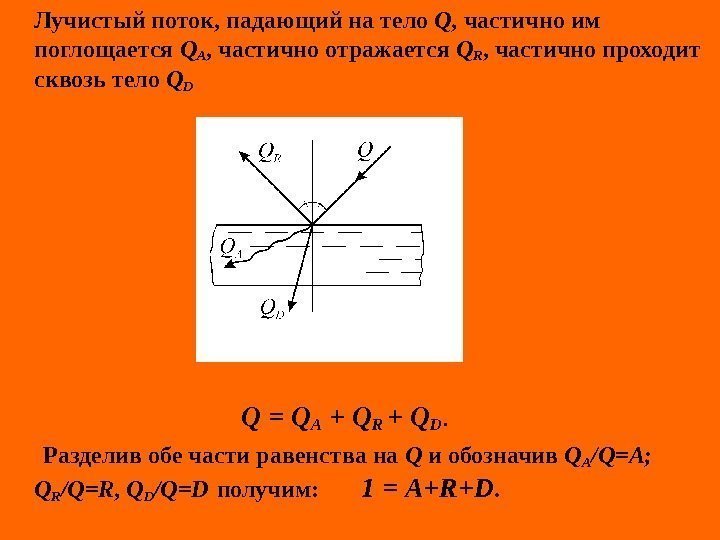
Лучистый поток, падающий на тело Q, частично им поглощается QA , частично отражается QR , частично проходит сквозь тело Q D Q = Q A + QR + QD. Разделив обе части равенства на Q и обозначив Q A /Q=A; Q R /Q=R , QD /Q= D получим : 1 = A+R+D.

Коэффициенты А, R, D характеризуют соответственно поглощательную, отражательную и пропускную (прозрачность) способности тела. В связи с этим они именуются коэффициентами поглощения, отражения и пропускания. Эти коэффициенты для различных тел могут меняться от 0 до 1. Тело, которое всю падающую на них лучистую энергию поглощает, QA =Q и А=1 (R=D=0), называют абсолютно черным. Тело, которое всю падающую на него лучистую энергию отражает, Q R =Q; R=1 (А=D =О), называют абсолютно белым или зеркальным. Тело, которое всю падающую на него лучистую энергию пропускает, Q D =Q; D=1 (А=R=О), называют абсолютно прозрачным. В природе абсолютно черных, белых и прозрачных тел не существует.

Коэффициенты А, R, D характеризуют соответственно поглощательную, отражательную и пропускную (прозрачность) способности тела. В связи с этим они именуются коэффициентами поглощения, отражения и пропускания. Эти коэффициенты для различных тел могут меняться от 0 до 1. Тело, которое всю падающую на них лучистую энергию поглощает, QA =Q и А=1 (R=D=0), называют абсолютно черным. Тело, которое всю падающую на него лучистую энергию отражает, Q R =Q; R=1 (А=D =О), называют абсолютно белым или зеркальным. Тело, которое всю падающую на него лучистую энергию пропускает, Q D =Q; D=1 (А=R=О), называют абсолютно прозрачным. В природе абсолютно черных, белых и прозрачных тел не существует.

Законы лучистого теплообмена Закон Планка устанавливает зависимость между спектральной интенсивностью излучения абсолютно черного тела и абсолютной температурой тела. Планк установил, что изменение интенсивности излучения по длинам волн для абсолютно черного тела подчиняется следующему закону где – интенсивность излучения абсолютно черного тела, Вт/м 3 ; с1 = 3, 74· 10 -16 Вт·м 2 — первая постоянная Планка; — длина волны, м ; с 2 = 0, 0144 м·К – вторая постоянная Планка. , 1 ec. E 1 Tc

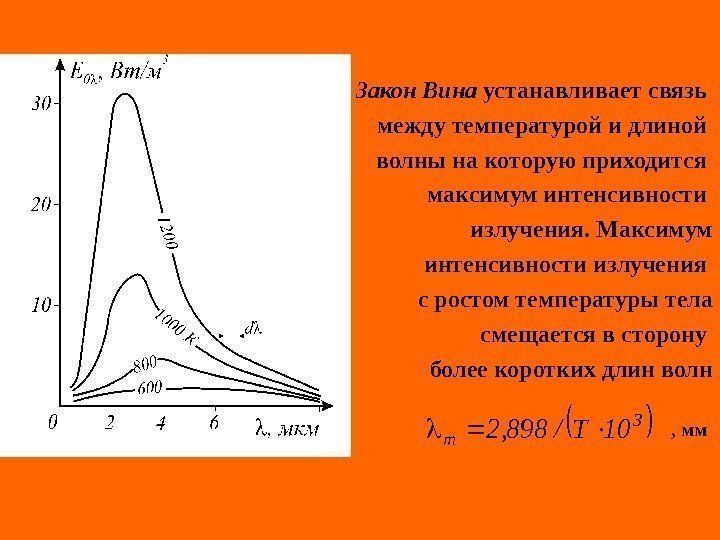
Закон Вина устанавливает связь между температурой и длиной волны на которую приходится максимум интенсивности излучения. Максимум интенсивности излучения с ростом температуры тела смещается в сторону более коротких длин волн , мм 3 m 10 T/898,

3 акон Стефана — Больцмана устанавливает связь между плотностью полусферического интегрального излучения абсолютно черного тела и абсолютной температурой тела. Плотность излучения абсолютно черного тела прямо пропорциональна абсолютной температуре в четвертой степени где σ0 , c 0 – коэффициенты пропорциональности (постоянные излучения); σ 0 = 5, 76· 10 -8 Вт/( м 2 ·K 4 ) ; c 0 = 5, 76 Вт/(м 2 ·K 4 ). Для серых тел закон Стефана-Больцмана записывается в виде , 100 T c. TЕ 4 00 4 100 T c. Е

Сопоставление плотностей излучения серого и абсолютно черного тел при одинаковой температуре приводит к характеристике, называемой степенью черноты ε где ε – степень черноты тела или относительная излучательная способность тел, которая меняется от нуля (абсолютно белое тело) до единицы (абсолютно черное тело). 3 акон Кирхгофа устанавливает связь между плотностью интегрального полусферического излучения и поглоща-тельной способностью тел , c c E E 00 , Tf. E A E A E 0 n n

3 акон Стефана — Больцмана устанавливает связь между плотностью полусферического интегрального излучения абсолютно черного тела и абсолютной температурой тела. Плотность излучения абсолютно черного тела прямо пропорциональна абсолютной температуре в четвертой степени где σ0 , c 0 – коэффициенты пропорциональности (постоянные излучения); σ 0 = 5, 76· 10 -8 Вт/( м 2 ·K 4 ) ; c 0 = 5, 76 Вт/(м 2 ·K 4 ). Для серых тел закон Стефана-Больцмана записывается в виде , 100 T c. TЕ 4 00 4 100 T c. Е

Сопоставление плотностей излучения серого и абсолютно черного тел при одинаковой температуре приводит к характеристике, называемой степенью черноты ε где ε – степень черноты тела или относительная излучательная способность тел, которая меняется от нуля (абсолютно белое тело) до единицы (абсолютно черное тело). 3 акон Кирхгофа устанавливает связь между плотностью интегрального полусферического излучения и поглоща-тельной способностью тел , c c E E 00 , Tf. E A E A E 0 n n

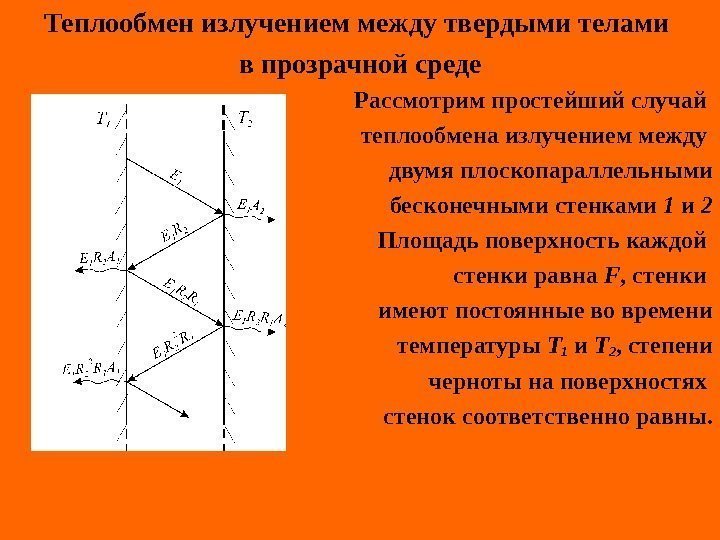
Теплообмен излучением между твердыми телами в прозрачной среде Рассмотрим простейший случай теплообмена излучением между двумя плоскопараллельными бесконечными стенками 1 и 2 Площадь поверхность каждой стенки равна F , стенки имеют постоянные во времени температуры T 1 и T 2 , степени черноты на поверхностях стенок соответственно равны.

Плотность излучения стенки 1 равна ; эта энергия достигает стенки 2 и там поглощается в количестве , а остальное ее количество отражается обратно на стенку 1. Дальнейшая судьба этого количества энергии видна из схемы Поглощаемая стенкой 1 плотность излучения за счет собственного излучения равна сумме бесконечного числа слагаемых [ ]. Выражение в скобках является убывающей геометрической прогрессией. Сумма бесконечного числа ее членов равна 121 ‘ 1. пог. E 1 E. . . 11111 2 2 2 121 .

Отсюда Наряду с поглощением энергии от собственного отраженного излучения первая стенка поглощает еще часть энергии, излучаемой второй стенкой. Вычисление этого добавочного количества поглощаемой энергии аналогично предыдущему Таким образом, стенка 1 испускает плотность излучения , а поглощает . Разность между плотностью излучения и поглощением равна тепловому потоку переданного от стенки 1 к стенке 2 . 111 E 21 121′ 1. пог . 111 E E 21 21» 1. пог 1 E » 1. пог.

где – общее количество лучистой энергии (эффективное излучение), излучаемое телом 1 ; – общее количество энергии (эффективное излучение), излучаемое стенкой 2 и падающее на стенку 1. Эффективное излучение включает в себя собственное излучение , а также отраженное, падающее на стенку 1 от стенки 2, Аналогично получается выражение для эффективного излучения стенки 2 в направлении стенки 1, QQQ 2121 1 Q 2 Q FE 1 121 Q 21221 QFEQ 12111 QFEQ

Подставляя выражения для и в уравнение и после преобразования получим расчетную формулу для определения результирующего количества энергии лучистого теплообмена между двумя плоскопараллельными поверхностями. где Q 1, 2 – тепловой поток, передаваемый излучением телом 1 телу 2 , Вт ; ε 1, 2 – приведенная степень черноты тел 1 и 2 , определяемая из выражения 1 Q 2 Q , 100 T Fc. Q 4 2 4 1 02, 1 . 1/1/1 1 21 2,

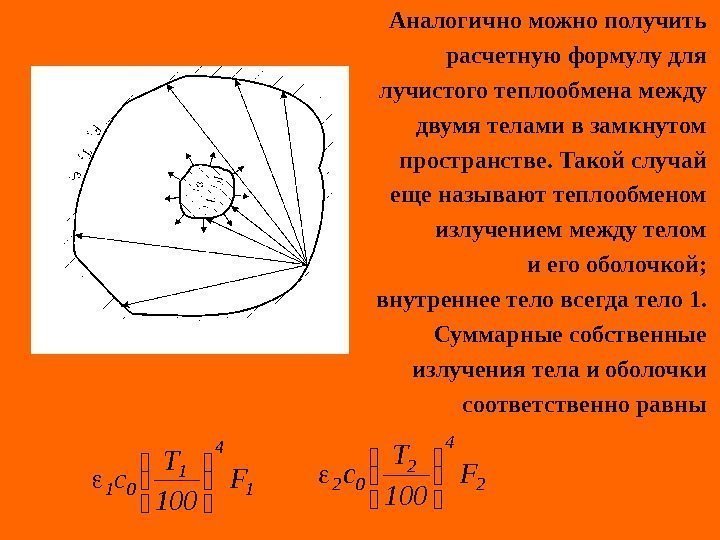
Аналогично можно получить расчетную формулу для лучистого теплообмена между двумя телами в замкнутом пространстве. Такой случай еще называют теплообменом излучением между телом и его оболочкой; внутреннее тело всегда тело 1. Суммарные собственные излучения тела и оболочки соответственно равны 1 4 1 01 F 100 T c 2 4 2 02 F 100 T c

Искомая величина Q 1, 2 будет результирующим излучением на поверхности тела и внутренней поверхности оболочки где – приведенная степень черноты, Если поверхность F 1 значительно меньше поверхности F 2 , то и расчетная формула принимает вид , 100 T Fc. Q 4 2 4 1 10 пр2, 1 пр . / F F / пр111 1 2 21 1 4 2 4 1 1012, 1 100 T Fc. Q

Обобщенное уравнение для расчета лучистого теплообмена между двумя телами любой формы и произвольного их расположения только в каждом частном случае для определения приведенных степени черноты и поверхности (для εпр и F ) имеются свои расчетные выражения. Для уменьшения количества лучистой энергии, падающей со стороны других тел на данное тело, необходимо уменьшать температуру тел, излучающих энергию и уменьшать степень их черноты. При невозможности проведения таких мероприятий или их недостаточной эффективности применяют экраны. Экраны изготовляются из материалов с малой степенью , 100 T Fc. Q 4 2 4 1 10 пр2,

Для оценки эффективности экрана получим расчетное соотношение для определения лучистого теплообмена между телами при наличии экранов. Данное расчетное уравнение получается из решения системы уравнений, каждое из которых характеризует теплообмен между телом 1 и экраном и телом 2 Установка одного экрана между двумя параллельными стенками уменьшает теплообмен излучением примерно в 2 раза, в общем случае при установке n экранов (степени черноты тел и экранов равны) лучистый теплообмен уменьшается в раз. , 100 T Fc’Q 4 2 4 1 10 пр2, 1 n i эiэiпрпр F F / ‘ 1 1 1 2 1 1 1 n

Расчетное уравнение лучистого теплообмена можно свести к виду пропорциональности теплового потока разности температур где — коэффициент лучистого теплообменаs 121 s 21 3 m 10 пр 4 2 4 1 10 пр2, 1 Ftttt 100 T Fc 04, 0 100 T Fc. Q 100 T c 04, 0 m 0 прs

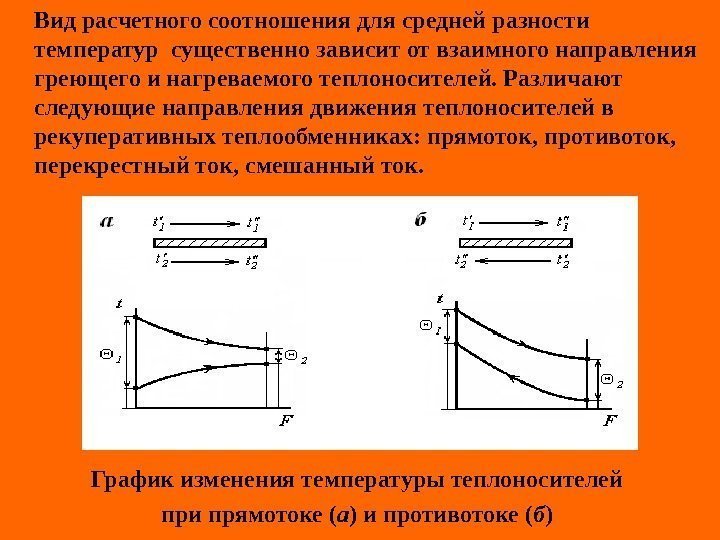
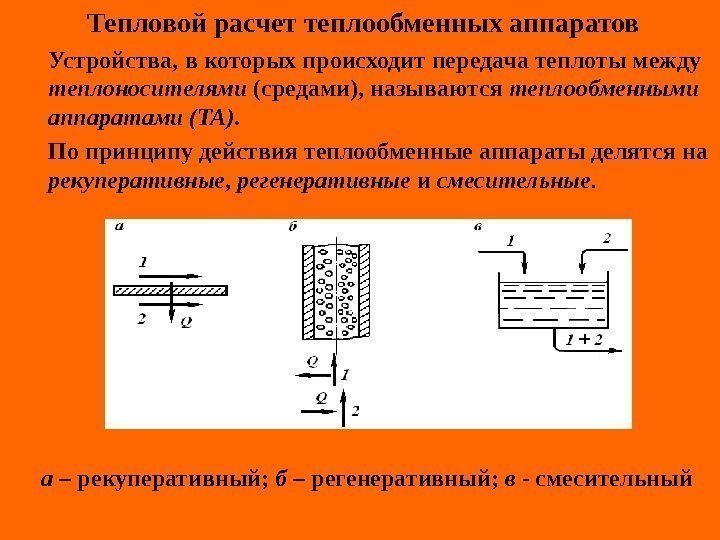
Сложный теплообмен (теплопередача ) Процесс передачи теплоты от одной среды (теплоносителя) к другой среде (теплоносителю) через разделяющую их стенку называется теплопередачей и состоит из процессов теплоотдачи от горячего теплоносителя к поверхности стенки, передачи теплоты теплопроводностью через многослойную (или однослойную) стенку и процесса теплоотдачи от поверхности стенки к холодному теплоносителю. При установившемся процессе теплопередачи средние температуры горячего и холодного теплоносителей (сред) остаются постоянными вдоль поверхности стенки, а тепловой поток сохраняет неизменное значение ( Q = const ).

Расчетная формула стационарного процесса теплопередачи имеет следующий вид: где Q – тепловой поток; k – коэффициент теплопередачи; F – площадь поверхность теплопередачи; = ( tm 1 – tm 2 ) – средний температурный напор (средняя разность температур). Коэффициент теплопередачи k выражает количество передаваемой теплоты в единицу времени через единицу площади поверхности при температурном напоре равном 1 градусу. В большинстве случаев при движении теплообменивающи — хся жидкостей вдоль поверхности теплообмена их температуры изменяются. Коэффициент теплопередачи также изменяется по поверхности теплообмена. срtk. FQ срt

Однако, во многих случаях можно рассматривать величину коэффициента теплопередачи постоянной по всей поверхности теплообмена, а разность температур между жидкостями принимать средней по поверхности теплообмена. В этом случае для определения теплового потока имеем Коэффициент теплопередачи имеет очень важное прикладное значение. Расчетные формулы для определения коэффициента теплопередачи, а также формулы для определения среднего температурного напора (средней разности температур) рассматриваются ниже. Ftdk. Q

Теплопередача чрез плоскую стенку Рассмотрим процесс передачи теплоты через плоскую стенку с площадью поверхности F , толщиной стенки , коэффициентом теплопроводности материала стенки , при известных температурах горячего и холодного теплоносителей, а также коэффициентов теплоотдачи от горячего и холодного теплоносителей. Температура на внешних поверхностях стенки неизвестны. При стационарном температурном поле системы тепловой поток и плотность теплового потока постоянны. 1 жt 2 жt

На основе закона Фурье и уравнения Ньютона – Рихмана можно написать: плотность теплового потока, передаваемого от горячего теплоносителя поверхности стенки та же плотность теплового потока передается теплопроводно-стью через стенку и передается от поверхности стенки к холодному теплоносителю1 с1 ж 11 tt F Q q 2 c 1 c 2 tt F Q q 2 с2 ж 23 tt F Q q

Решая эти уравнения относительно разности температур, находим: Складывая по частям выражения разностей температур и учитывая, что получим выражение для итоговой разности температур. q. Rq 1 tt ; q. Rq 1 tt 333 2 2 ж 2 c 222 1 1 2 c 1 c 111 1 1 c 1 ж 321 qqqq , Rqq. RRRq 11 tt 321 21 1 1 2 ж 1 ж

где – термическое сопротивление теплопередачи плоской стенки ( м 2 К\ Bm ); ; – термические сопротивления теплоотдачи со стороны горячего теплоносителя, теплопроводности плоской стенки и термические сопротивления теплоотдачи со стороны холодного теплоносителя соответственно. Отсюда, следует выражение для плотности теплового потока (уравнение теплопередачи плоской стенки): 321 RRRR ; 1 R 11 2 R 2 3 1 R ; ttktt R 1 q 2 ж 1 жttk. Fq. FQ

где k =1/R – коэффициентом теплопередачи плоской стенки, Вт/(м 2 · К ) После определения количества передаваемой теплоты ( Q , q ) можно найти температуры на поверхностях стенки из выражений разности температур: , 11 1 RRR 1 k 21 321 2 2 ж 1 1 ж 1 с 1 qtt 1 1 ж 2 2 ж 2 с 1 qtt

В случае теплопередачи через многослойную стенку, состоящую из n слоев тепловой поток и плотность теплового потока и следовательно коэффициент теплопередачи определяются с учетом термических сопротивлений каждого слоя Температура поверхности и на стыке слоев определяется из тех же соображений, что и для однослойной стенки. 11 1 RRR 1 k 2 ni 1 ii i 1 321 i 1 i i 1 1 ж 1 ic 1 qtt

Теплопередача через цилиндрическую стенку Рассмотрим процесс передачи теплоты между средами через однородную стенку трубы длиной l c внутренним диаметром d 1 и наружным диаметром d 2. Коэффициент теплопроводности материала стенки трубы — λ. Внутри трубы движется горячий теплоноситель со средней температурой t ж 1 , с наружи – холодный теплоноситель со средней температурой t ж 2. Температуры стенки на внутренней tс1 и наружной t с2 поверхности трубы неизвестны. Коэффициенты теплоотдачи со стороны горячего и холодного теплоносителя равны и соответственно. При стационарном температурном поле системы тепловой поток ( Q ) постоянен.

Тепловой поток, передаваемый от горячего теплоносителя к поверхности стенки тот же самый тепловой поток передается теплопроводностью через стенку и передается от поверхности стенки к холодному теплоноси-телюldtt. Q 11 с1 ж 1 2 c 1 c 1 2 tt d d ln l 2 Q ldtt. Q 22 с2 ж

Решая уравнения относительно разности температур и суммируя полученные выражения, получим расчетное уравнение для определения теплового потока Q где kl – линейный коэффициентом теплопередачи для цилиндрической однородной стенки, Вт/(м ·К) 2 ж 1 жlttlk. Q 221 2 11 l l d 1 d d ln 2 1 d 1 1 R 1 k 221 2 11 l d 1 d d ln 2 1 d 1 R

После определения величины теплового потока Q можно найти температуры на поверхности стенки: В случае многослойной стенки, состоящей из n слоев, тепловой поток и плотность теплового потока определяются с учетом того, что линейное термическое сопротивление определяются с учетом термических сопротивлений каждого слоя. ld Q t d d ln 2 1 d 1 ( l Q tt ; ld Q tt 22 2 ж 1 2 11 1 ж 2 с 11 1 ж 1 с . d 1 d d ln 2 1 d 1 R n 1 i 1 i 2 i 1 i i 11 l

Уравнение теплопередачи для криволинейной поверхности Для криволинейных стенок произведение k. F неразделимо, для определения теплового потока можно воспользоваться уравнением теплового потока для плоской стенки, для этого водится понятие средней поверхности каждого слоя стенки ( Fmi ) где KF – неразделимый комплекс называемый водяным эквивалентом поверхности теплопередачи 2 ж 1 ж ttk. FQ 1 n 2 ni 1 imii i 11 321 F 1 FF 1 1 RRR 1 k.

где Fmi – средняя поверхность теплопередачи, в частном случае определяемая: для плоской стенки – средняя арифметическая поверхность (справедлива также и для тонкостенных цилиндрических систем), для цилиндрической поверхности – средняя логарифмическая поверхность, для сферической поверхности – средняя геометрическая поверхность. Расчетная поверхность теплопередачи для криволинейных стенок определяется из выражения 2 FF FF 21 mami i 1 i mi i 1 i mlmi d d ln dd ld F F ln FF FF 1 iim. Gmi.

В технических расчетах чаще всего приходится решать проблему двух видов: уменьшение тепловых потерь (изоляция поверхности теплообмена) и увеличение количества передаваемого тепла (интенсификация теплопередачи). Изоляция криволинейных поверхностей теплообмена имеет свои особенности. Рассмотрим покрытие изоляцией однослойной цилиндричес-кой стенки. . F 1 FF 1 11 k k. F F 1 i 2 n 1 ii, mi i 11 2 n 1 ii i

Линейное термическое сопротивление стенки Из уравнения видно, что при увеличении толщины изоляции d 3 термическое сопротивление R lu = 1/(2·λ и )· lnd 3 / d 2 увеличивается, а термическое сопротивление R l 2 = 1/( α 2 · d 3 ) уменьшается; термические сопротивления R l 1 = 1/( α 1 · d 1 ) и R lc = 1/(2·λ c )· ln ( d 2 / d 1 ) сохраняют постоянное значение. При этом суммарное термическое сопротивление R l сначала умень-шается, а затем увеличивается, а удельный линейный тепловой поток q l наоборот, сначала возрастает, а потом уменьшается. Диаметр изоляции, при котором суммарное термическое сопротивление имеет минимальное значение, а удельный линейный тепловой поток максимальное, назы-вается критическим ( d 3 = d кр ) и определяется по формуле . RRRR d 1 d d ln 2 1 d 1 R 2 llиlc 1 l 322 3 из 1 2 c 11 l

При наложении изоляции на трубу поступают следующим образом: выбрав какой-либо теплоизоляционный материал по известным α 2 и λu рассчитывают dкр. Если окажется, что dкр > d 2 , то применение выбранного материала в качестве тепловой изоляции нецелесообразно. Таким образом, для эффективного применения тепловой изоляции необходимо, чтобы d кр ≤ d 2 , а λu ≤ α 2 · d 2 /2. Из выражения ( ) следует, что чем больше q , тем больше тепловой поток, т. е. задача интенсификации теплообмена сводится к увеличению удельного теплосъема. Увеличить q можно путем повышения ∆ t и k. . 2 d 2 и кр Fqttk. Ftt R 1 Q 2 ж 1 ж

Увеличение ∆ t может быть связано с изменением технологии процесса, что не всегда возможно. Увеличить k можно за счет повышения коэффициентов теплоотдачи. При этом, как уже говорилось, при большом различии α 1 и α 2 коэффициент теплопередачи всегда меньше минимального α. Таким образом, увеличить k и интенсифицировать теплообмен можно двумя путями: при α 1 << α 2 или α 2 << α 1 – повышением меньшего коэффициента теплоотдачи; при α 1 ≈ α 2 – повышением обоих коэффициентов или любого из них. Помимо увеличения коэффициентов теплоотдачи интенсифицировать процесс теплопередачи можно за счет оребрения поверхности теплоотдачи. Оребряется та поверхность, со стороны которой α меньше; теоретическим пределом оребрения является равенство термических сопротивлений теплоотдачи 1/( α 1 F 1 ) = 1/(α 2 F 2 ) в итоге увеличивается произведение k. F и повышается Q.

Теплопередача при изменяющихся температурах вдоль поверхности теплообмена В теплообменных аппаратах и теплоиспользующих устройствах температура греющего и нагреваемого теплоносителей изменяются вдоль поверхности теплообмена: температура греющего теплоносителя понижается, а температура нагреваемого повышается. Исключение составляют теплообменные аппараты, в которых с одной стороны поверхности испаряется жидкость или конденсируется пар(например испарители или конденсаторы). В условиях изменяющихся температур теплоносителей уравнение теплопередачи для элементарной площади можно записать в следующем виде: iiid. Ftk. Q

Тепловой поток передаваемый через всю поверхность теплообмена при постоянном коэффициенте теплопередачи k равен Для учета изменения температур теплоносителей по поверхности теплообмена в расчетное уравнение теплопередачи вводится средняя разность температур (средний температурный напор), который определяется уравнением где — средняя разность температур. F id. Ftk. Q F iimd. Ft F 1 m m m k. FQ

Вид расчетного соотношения для средней разности температур существенно зависит от взаимного направления греющего и нагреваемого теплоносителей. Различают следующие направления движения теплоносителей в рекуперативных теплообменниках: прямоток, противоток, перекрестный ток, смешанный ток. График изменения температуры теплоносителей при прямотоке ( а ) и противотоке ( б )

Пренебрегая падением давления теплоносителей при движении, т. е. считая процесс протекающим изобарным, из первого начала термодинамики имеем где Q – мощность теплообменного аппарата, Вт ; и – расход горячего и холодного теплоносителей соответственно, кг\с ; и –изменение удельной энтальпии греющего и нагреваемого теплоносителей соответственно, Дж\кг. Для конвективных теплообменных аппаратов (в процессе теплообмена отсутствуют фазовые переходы) в силу того, что имеем 221121 h. GQQQ 1 G 2 G 1 h 2 h tch pm 21121 pm 2 11 pm 121 t. Wtc. GQQQ

где cpm 1 и cpm 2 – средние теплоемкости горячего и холодного теплоносителей; W 1 = G 1 · cpm 1 и W 2 = G 2 · cpm 2 – водяные эквиваленты горячего и холодного теплоносителей. В силу того, что для теоретического процесса теплопередачи в ТА, тепловой поток определенный из уравнение теплового баланса равен тепловому потоку определенному по уравнению теплопередачи имеем Расчетные соотношения для определения средней разности температур простейших схем взаимного движения теплоносителя: прямотока и противотока получаются из выражения записанного для элементарного участка теплообмена m 21121 k. Ft. WQQQ

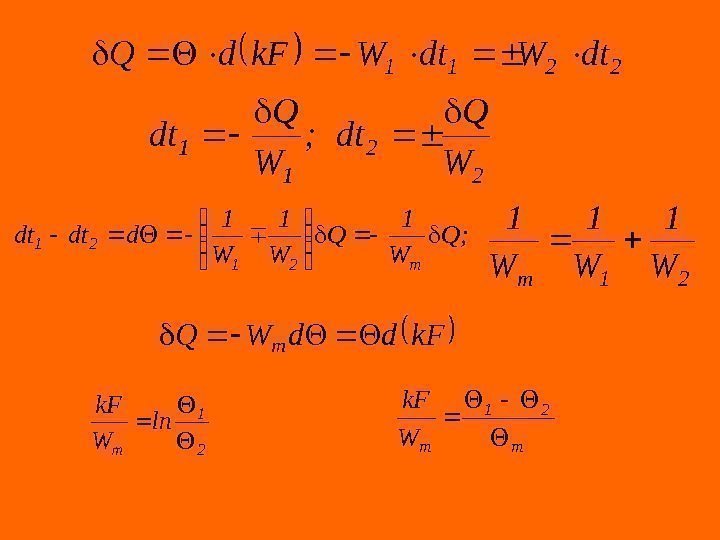22 11 W Q dt; W Q dt ; Q W 1 W 1 ddtdt m 21 21 21 m. W 1 W 1 k. Fdd. WQm 2 1 m ln W k. F m 21 m W k. F 2211 dt. Wk. Fd. Q

Расчетное уравнение средней разности температур справедливое для схем прямотока и противотока, называется среднелогарифмической разностью температур или уравнением Грасгофа. для схемы прямоток для схемы противоток 2 1 21 mlmln 211 tt 212 tt; ; tt 211 212 tt

При незначительном изменении температуры теплоносителей вдоль поверхностей теплообмена вместо среднелогарифмической разности температур можно пользоваться среднеарифметической разностью температур Для определения средней разности температур между теплоносителями для схем с перекрестным и смешанным током теплоносителей используются два метода: графоаналитический и методика предложенная профессором Н. И. Белоконем. Согласно графоаналитическому методу , предварительно по формуле Грасгофа подсчитывается среднелогарифмическая разность температур для противоточного теплообменного аппарата 2 tt 2211 mаm

Затем с учетом схемы движения теплоносителей (число ходов по трубному и межтрубному пространству) из графиков определяется коэффициент t = f(PS и R ) ; )tt( PS 21 22 ; W W )tt( R 1 2 22 11 m. Ltm

Н. И. Белоконь предложил обобщенное уравнение для определения средней разности температур справедливое для любых схем движения теплоносителей — характеристическая разность температур, Wm – приведенный водяной эквивалент теплоносителей, ; ln II I III m ; T 5, 0 ma. II T 21 2 21 m. WW p 4 ) W 1 ( W 1 21 2 21 tt. P 4 tt. T

Индекс противоточности р определяется как отношение водяного эквивалента поверхности теплообмена, где осуществляется противоточная схема движения теплоносителей ( k. F ) прот , и водяного эквивалента поверхности теплообмена всего ТА ( k. F ) Для прямоточной схемы индекс противоточности равен p = 0 , а при противотоке p = 1 и в этом случае уравнение Белоконя совпадает с уравнением Грасгофа. ])k. F()k. F[( )k. F( p прямпрот

Тепловой расчет теплообменных аппаратов Устройства, в которых происходит передача теплоты между теплоносителями (средами), называются теплообменными аппаратами (ТА). По принципу действия теплообменные аппараты делятся на рекуперативные , регенеративные и смесительные. а – рекуперативный; б – регенеративный; в — смесительный

В рекуперативных ТА горячий и холодный теплоносители одновременно подаются в аппараты, омывая с разных сторон поверхность теплообмена, а тепловой поток передается от горячего к холодному теплоносителю через разделяющую их стенку. В регенеративных ТА горячий и холодный теплоносители омывают одну и ту же поверхность теплообмена последовательно. При омывании поверхности теплообмена горячий теплоноситель отдает ей теплоту, а затем ту же поверхность омывает холодная теплоноситель, который, получая теплоту, нагревается. Примером регенеративных ТА могут служить аппараты насадочного типа. В рекуперативных и регенеративных ТА в процессе теплопередачи между теплоносителями участвует поверхность теплообмена, поэтому эти аппараты называются поверхностными.

В смесительных ТА теплопередача между теплоносителями осуществляется путем их непосредственного смешения. Эти ТА называются контактными. Примером таких ТА могут быть градирни, в которых оборотная вода охлаждается атмосферным воздухом. По назначению теплообменные аппараты делятся на конвективные ( нагреватели и холодильники ), испарители, конденсаторы и кристаллизаторы. В конвективных ТА не происходит агрегатного превращения теплоносителей. В испарителях происходит испарение холодного теплоносителя или компоненты холодного теплоносителя. В конденсаторах конденсируется горячий теплоноситель или компонент горячего теплоносителя. Кристаллизаторы используются для охлаждения потока горячего теплоносителя до температуры, обеспечивающей образование кристаллов некоторых компонент горячего теплоносителя.

Основы теплового расчета рекуперативных теплообменных аппаратов В зависимости от постановки задачи тепловой расчет теплообменных аппаратов может быть конструктивным (расчеты первого рода) или поверочными (расчеты второго рода). При конструкторском тепловом расчете известны: вид теплоносителя, температура теплоносителей на входе и выходе из теплообменного аппарата, а также расходы теплоносителей. Определяют тепловую мощность и площадь поверхности теплообменного аппарата (ТА), с дальнейшим конструированием нового или выбором стандартного аппарата. При поверочный тепловом расчете известны: тип, характеристика и геометрические размеры ТА, вид и расходы теплоносителей, а также температуры теплоносителей на входе в теплообменник. Необходимо определить мощность теплообменного аппарата и температуры теплоносителей на выходе из теплообменника.

В основу теплового расчета рекуперативных ТА положены: уравнение теплового баланса и обобщенное уравнение теплопередачи при переменных температурах На первом этапе определяется мощность теплообменного аппарата из теплового баланса. Рассчитывается коэффициент теплопередачи К коэффициенты теплоотдачи, а также значения термических сопротивлений загрязнений и стенки теплообменной трубы находятся по справочной литературе. 21 QQQ mk. FQ , 11 1 k 2 ni 1 i ii

Конструируемый или выбираемый стандартный теплообменный аппарат способен обеспечить заданные температурные режимы теплоносителей, если его индекс противоточности при заданных температурных режимах и водяных эквивалентах теплоносителей больше или равен минимальному индексу противоточности pmin Определяется средняя разность температур для выбранной схемы )tt()tt( p 2211 1221 min ; ln II I III m

определяется расчетная площадь поверхности теплообмена Затем оцениваются площади проходных сечений трубного и межтрубного пространства (при условии достижения оптимальных скоростей движения теплоносителей) На базе полученных расчетных значениях площади теплообмена и проходных сечений либо определяются расчетным путем геометрические характеристики теплообменного аппарата (число ходов, диаметр, длина, количество , схема расположения трубок, число сегментных перегородок и т. д. ) либо из каталога выбирается стандартный теплообменный аппарат m р K Q F w G f

Конечным этапом конструктивного расчета является поверочный расчет целью которого является проверка соответствия выбранного (сконструированного) теплообменного аппарата с необходимым (конечные температуры теплоносителей). Действительная тепловая мощность теплообменного аппарата рассчитывается по формуле Н. И. Белоконя Действительные характеристики теплоносителей на выходе из теплообменного аппарата определяются из уравнения теплового баланса 1 1111 )(2 21 21 m. ТА WFk m ТА e e WWW tt Q 211 t. WQ