ТЕОРИЯ ВЕРОЯТНОСТЕЙ Основные понятия Этапы развития теории

ТЕОРИЯ ВЕРОЯТНОСТЕЙ Основные понятия

Этапы развития теории вероятностей » 2 -я половина XVI века – первые задачи » по теории вероятностей. Л. Пачоли Д. Кардано Н. Тарталья Б. Паскаль Я. Бернулли А. Муавр • Конец XVII- начало XIX века – П. Лаплас • формирование как самостоятельной С. Пуассон • научной дисциплины. • Конец XIX – конец XX века – • современный этап развития. П. Л. Чебышёв А. А. Марков А. М. Ляпунов А. Я. Хинчин А. Н. Колмогоров

Основные понятия • Стохастический эксперимент • ( испытание, опыт) – • - это такой эксперимент, результаты которого заранее нельзя предугадать. • Примеры. – – 1. Бросание монеты; 2. Выстрел по мишени; 3. Бросание игральной кости (кубика); 4. Измерение физической величины (длины изделия, влажности или температуры, давления)

Основные понятия • Случайное событие – • - это такое событие, которое может произойти (наступить) или не произойти в результате данного эксперимента. – Обозначения событий: A, B, C, …, ω, … – Пример 1. Бросание монеты. • А=(выпадение герба) • B=(выпадение цифровой надписи)

Основные понятия – Пример 2. Бросание игральной кости. • • =(выпадение цифры 1) =(выпадение цифры 2) --------=(выпадение цифры 6) А=(выпадение четного числа) В=(выпадение числа, меньше чем 4) --------

Основные понятия • Рассмотрим множество всех событий, которые могут произойти или не произойти в данном эксперименте. – Невозможное событие – событие, которое – не может наступить в данном эксперименте - Ǿ. – Достоверное событие – событие, которое обязательно произойдет в данном эксперименте – Ω.

Основные понятия – Пример 2. Бросание игральной кости. • =(выпадение цифры 1) • =(выпадение цифры 2) • -------- • =(выпадение цифры 6) • А=(выпадение четного числа) • В=(выпадение числа, меньше чем 4) • -------- • Ǿ=(выпадение числа, больше чем 6) • Ω=(выпадение какого-либо числа от 1 до 6)

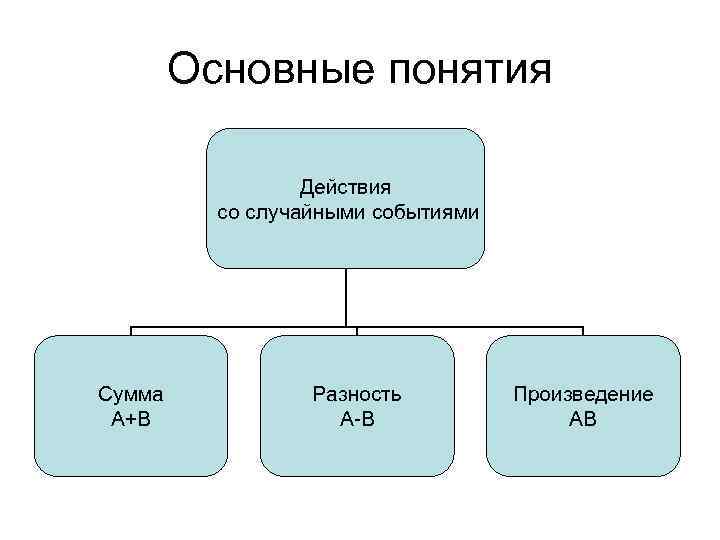Основные понятия Действия со случайными событиями Сумма А+В Разность А-В Произведение АВ

Основные понятия • Сумма двух событий А и В – это такое событие С=А+В, которое происходит тогда и только тогда, когда наступает хотя бы одно из событий А и В. • Разность двух событий А и В – это такое событие С=А-В, которое происходит тогда, когда А – наступает, а В – не наступает. • Произведение двух событий А и В – это такое событие С=АВ, которое происходит тогда и только тогда , когда наступают и А и В вместе.

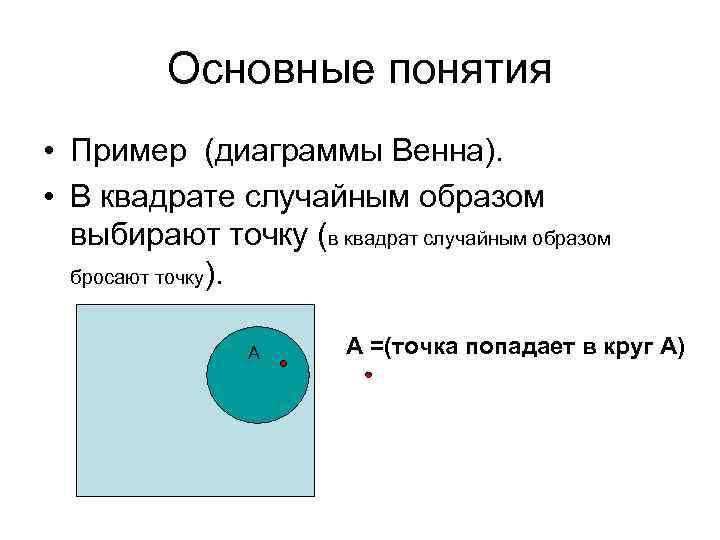Основные понятия • Пример (диаграммы Венна). • В квадрате случайным образом выбирают точку (в квадрат случайным образом бросают точку). А А =(точка попадает в круг А)

Основные понятия В=(точка попадает в треугольник В) А+В=(точка попадает хотя бы в одну фигуру А и В). А В

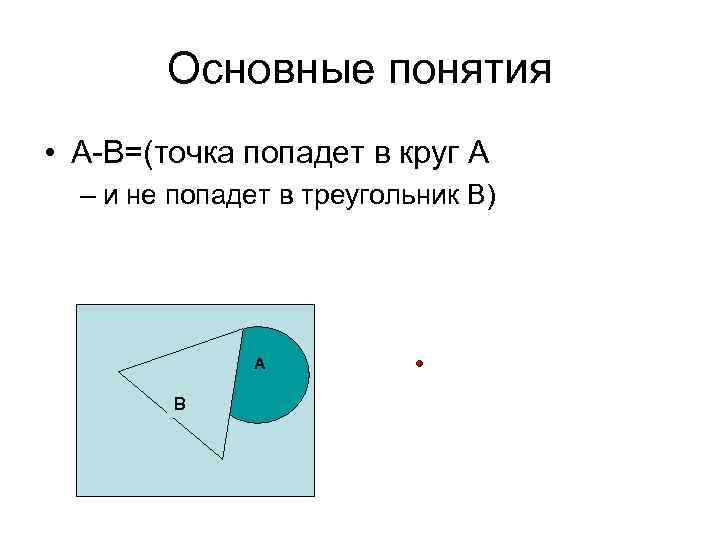Основные понятия • А-В=(точка попадет в круг А – и не попадет в треугольник В) А A В

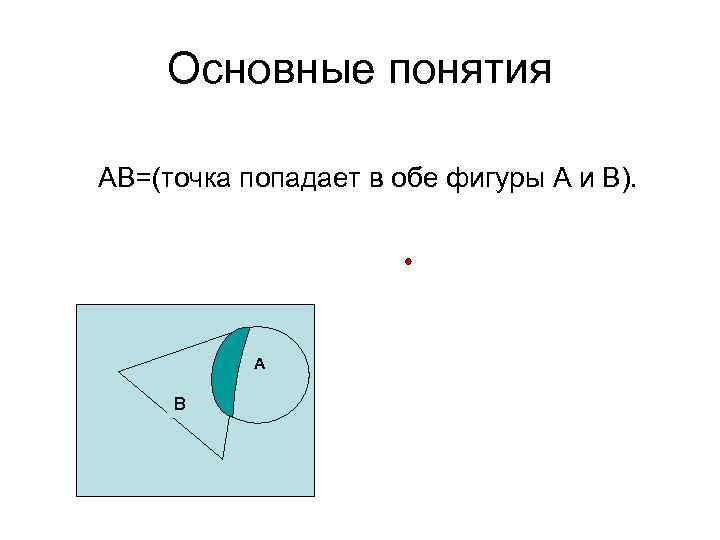Основные понятия АВ=(точка попадает в обе фигуры А и В). A В

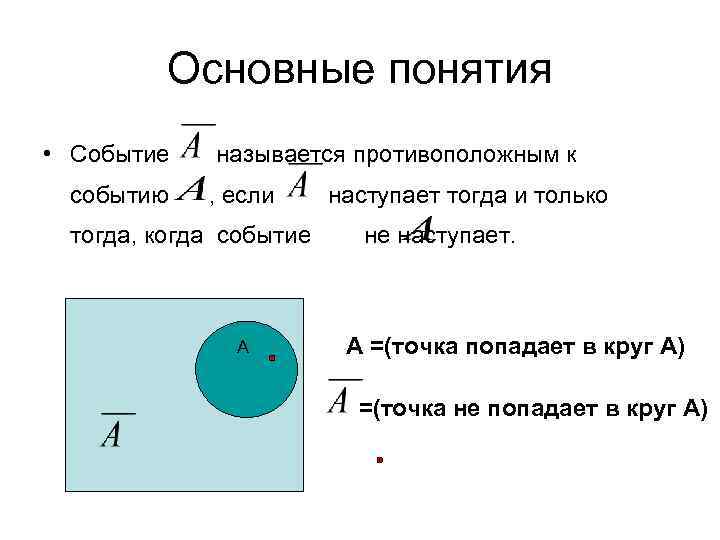Основные понятия • Событие событию называется противоположным к , если тогда, когда событие А наступает тогда и только не наступает. А =(точка попадает в круг А) =(точка не попадает в круг А)

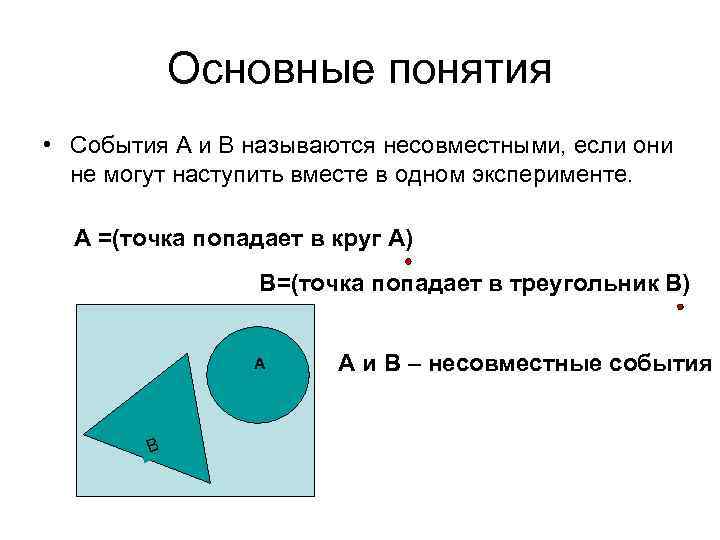Основные понятия • События А и В называются несовместными, если они не могут наступить вместе в одном эксперименте. А =(точка попадает в круг А) В=(точка попадает в треугольник В) A В А и В – несовместные события

Свойства операций • • А+В=В+А (А+В)+С=А+(В+С) А+Ǿ=А А+Ω=Ω (Д. з. ) АВ=ВА А(ВС)=(АВ)С АǾ=Ǿ АΩ=A Ǿ (А+В)С=АC+BС

Пространство элементарных событий » Рассмотрим стохастический эксперимент. 1. События ω взаимно исключают друга. 2. В результате эксперимента обязательно наступает какое –либо одно из них. 3. Для любого события А, по наступлению события ω можно сказать о том, наступило или не наступило событие А. События ω - элементарные.

Пространство элементарных событий – Пример 3. Бросание игральной кости. • • =(выпадение цифры 1) =(выпадение цифры 2) --------=(выпадение цифры 6)

Пространство элементарных событий • Пример 4. – Завод выпускает N однотипных изделий. – Для оценки качества выбирают и исследуют m изделий. ω – любой набор из m изделий. - пространство элементарных событий.

Определение вероятности • Рассмотрим стохастический • эксперимент. - конечное или счетное множество элементарных событий.

Определение вероятности P(Ǿ)=0 • Свойства вероятности: • 1) • 2)

Частота события • Пусть n – число повторений одного и того же стохастического эксперимента. • m(A) – число наступлений события А. • Проводятся различные серии из n повторений одного и того же стохастического эксперимента при • Определение. • Событие А называется стохастически устойчивым, • если • В этом случае Р(А)=р.

Частота события • Пример. Бросание монеты. • А=(выпадение герба). • Бюффон (XVII век). n=4040, m(A)=2048. • К. Пирсон (конец XIX века). n=24000, m(A)=12012. P(A)=0, 5

Классическая схема -пространство элементарных событий - конечное (i=1, … , n). Пусть событие А может наступить при наступлении m элементарных событий

Классическая схема – Пример 3. Бросание игральной кости. • • =(выпадение цифры 1) =(выпадение цифры 2) --------=(выпадение цифры 6) Равновозможные события А=(выпадение четного числа) В=(выпадение числа, меньше чем 4)

Геометрическая схема • Пример. • В квадрате случайным образом выбирают точку (в квадрат случайным образом бросают точку). А А =(точка попадает в круг А)

Геометрическая схема • На фигуре Ф случайным образом выбирают точку (любое положение точки равновозможно). • А=(точка попадает в область А). Ф А

Геометрическая схема • Пример. • На отрезок длины L наугад бросается точка. Какова вероятность того, что она упадет не дальше, чем на расстоянии m от середины отрезка. • Решение. А=(точка упадет не далее, чем на расстоянии m от середины ) = (точка попадает на отрезок длины 2 m) 2 m L

Основные теоремы • Рассмотрим вероятностное пространство ( Ω, A , Р ). • Теорема 1 (вероятность противоположного события). • Ає A Ā є A, • Доказательство. • • Ǿ

Основные теоремы • Теорема 2 (вероятность суммы событий). • А, В є A • Доказательство. Ǿ • А В Ǿ

Условная вероятность • Определение. • Пусть Р(А)>0. Условной вероятностью Р(В/А) события В при условии, что событие А наступило, называется число • Обозначения: • Условная вероятность удовлетворяет всем аксиомам вероятности. В частности, •

Основные теоремы • Теорема 3 (вероятность произведения событий). • А, В є A • Доказательство. • По определению:

Независимые события • • • Определение. Пусть Р(А)>0 и Р(В)>0. Событие А не зависит от В, если Следствие. Если событие А не зависит от В, то и событие В не зависит от А. • Доказательство.

Независимые события • Определение. • События А и В называются независимыми, если • На практике из физической независимости событий делают вывод о теоретико-вероятностной независимости.

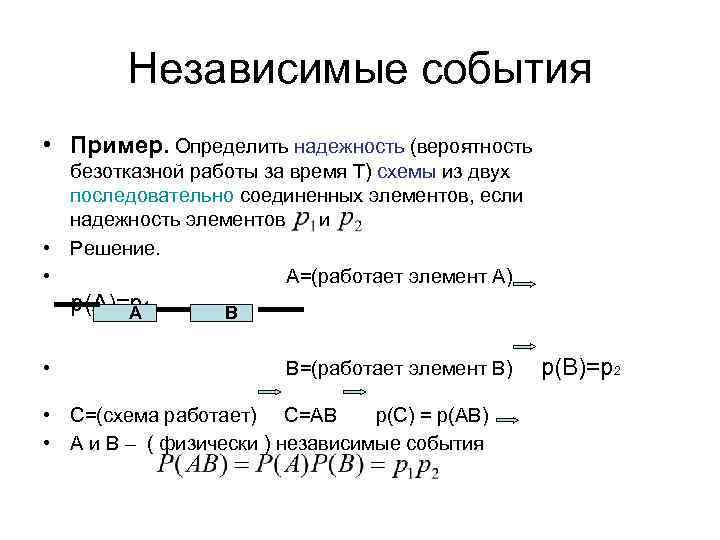Независимые события • Пример. Определить надежность (вероятность безотказной работы за время Т) схемы из двух последовательно соединенных элементов, если надежность элементов и • Решение. • А=(работает элемент А) р(А)=р1 А • В В=(работает элемент В) • С=(схема работает) С=АВ р(С) = р(АВ) • А и В – ( физически ) независимые события р(В)=р2

Независимые события • Теорема 4 (вероятность наступления хотя бы одного события). • Пусть А и В независимые события, р(А)=р1, р(В)=р2, • С=(наступит хотя бы одно из событий А и В). • Обозначим: • Тогда • Доказательство.

Полная группа событий • События образуют полную группу, если они • 1) попарно несовместны • 2) в результате эксперимента обязательно какоелибо одно из них наступит • • Пример 1. В стохастическом эксперименте рассмотрим события Они образуют полную группу. - гипотезы

Полная группа событий – Пример 2. Бросание игральной кости. • • =(выпадение цифры 1) =(выпадение цифры 2) --------=(выпадение цифры 6) - полная группа событий • • • Пусть А=(выпадение четного числа) и В=(выпадение нечетного числа) События А и В образуют полную группу.

Формула полной вероятности • Теорема. • Если события • образуют полную группу и события А справедлива формула , то для любого

Формула полной вероятности • Пример 2. • Три бригады ведут укладку бетонных блоков. • Первая бригада выполняет 50% всего объема работ, вторая 30% и третья – все остальное. • Вероятность появление брака для первой бригады равна 0, 05, второй – 0, 06 и третьей – 0, 1. • Найти вероятность того, что случайно выбранный и проверенный блок оказался установлен с нарушением технологии.

Формула полной вероятности • Решение. А=(блок установлен с нарушением технологии)

Формула Байеса • Теорема. • • • Пусть события образуют полную группу. Пусть событие А наступило ( Р(А)>0 ). Тогда вероятность того, что при этом была реализована гипотеза вычисляется по формуле

Формула Байеса • Пример 3. • Три бригады ведут укладку бетонных блоков. • Первая бригада выполняет 50% всего объема работ, вторая 30% и третья – все остальное. • Вероятность появление брака для первой бригады равна 0, 05, второй – 0, 06 и третьей – 0, 1. • Случайно выбранный и проверенный блок оказался установлен с нарушением технологии. • Какова вероятность того, что он был уложен третьей бригадой ?

Формула Байеса • Решение. • Из примера 2 :

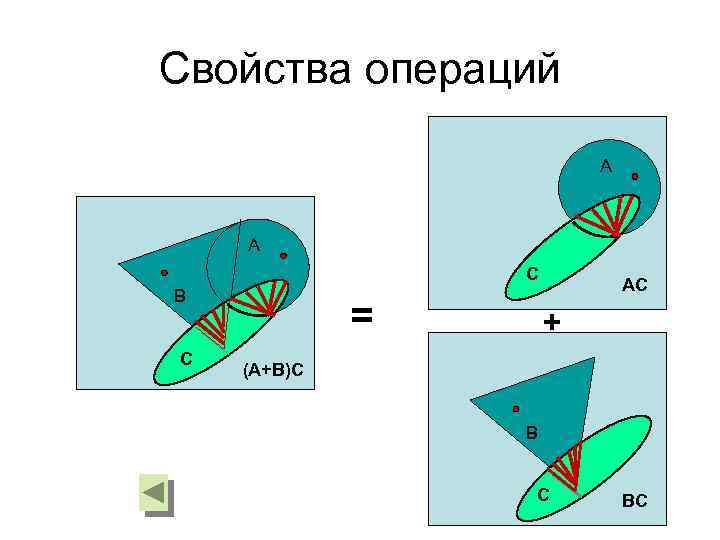Свойства операций А А C В C = AC + (A+B)C В C BC